Cho hai số phức z1,z2 thỏa mãn z1−3−4i=1 và z2−3−4i=12. Gọi số phức z = a + bi thỏa mãn 3a – 2b = 12. Giá trị nhỏ nhất của P=z−z1+z−2z2+2 bằng

Câu hỏi:

Cho hai số phức $z_1,z_2$ thỏa mãn $\left|z_1-3-4i\right|=1$ và $\left|z_2-3-4i\right|=\frac{1}{2}.$ Gọi số phức z = a + bi thỏa mãn 3a – 2b = 12. Giá trị nhỏ nhất của $P=\left|z-z_1\right|+\left|z-2z_2\right|+2$ bằng

A. $P_{\min }=5-2\sqrt{3}.$

B. $P_{\min }=\frac{\sqrt{9945}}{13}.$

Đáp án chính xác

C. $P_{\min }=5+2\sqrt{5}.$

C. $P_{\min }=\frac{\sqrt{9945}}{11}.$

Trả lời:

Chọn B.
Có $\left|z_2-3-4i\right|=\frac{1}{2}\iff \left|2z_2-6-8i\right|=1.$
Gọi $A\left(x_1;y_1\right),C\left(x_3;y_3\right),M\left(a;b\right)$ lần lượt là các điểm biểu diễn $z_1,2z_2,z.$
Ta có: $A\left(I;1\right):{\left(x-3\right)}^2+{\left(y-4\right)}^2=1,$ với I(3; 4).
$C\left(J;1\right):{\left(x-6\right)}^2+{\left(y-8\right)}^2=1,J\left(6;8\right)$
$M\in \Delta :3x-2y=12$
Khi đó: $P=\left|z-z_1\right|+\left|z-2z_2\right|+2=MA+MC+2.$
Bài toán trở thành tìm giá trị nhỏ nhất của biểu thức $P=MA+MC+2$ khi A, C chạy trên 2 đường tròn cố định (I; 1) và (J; 1) nằm cùng phía với đường thẳng $\Delta :3x-2y=12$ và điểm M thuộc đường thẳng $\Delta :3x-2y=12.$

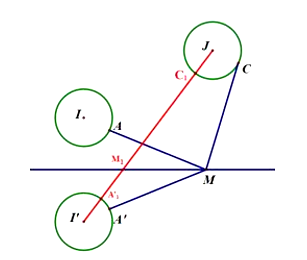
Gọi đường tròn đối xứng với (I; 1) qua đường thẳng $\Delta :3x-2y=12$ là (I’; 1). Suy ra $I‘\left(\frac{105}{13};\frac{8}{13}\right).$
Vì A’ đối xứng với A qua $\Delta$ nên $MA+MC=MA‘+MC\ge A_1‘C_1=II‘-I‘A_1‘-I{C}_1=II‘-2$ nên $P_{\min }=JI‘=\frac{\sqrt{9945}}{13}.$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Đồ thị hàm số y=x2−x+1x+1 cắt trục tung tại điểm có tung độ bằng 
   
   

   Câu hỏi:
   

   Đồ thị hàm số $y=\frac{x^2-x+1}{x+1}$ cắt trục tung tại điểm có tung độ bằng 

   A. 1                             

   Đáp án chính xác

   B. -1                           

   C. 2                             

   D. 0

   Trả lời:

   Chọn A.
   Đồ thị hàm số $y=\frac{x^2-x+1}{x+1}$ cắt trục tung nên hoành độ giao điểm bằng 0 suy ra tung độ giao điểm bằng 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Với a là số thực dương tùy ý, a23 bằng: 
   
   

   Câu hỏi:
   

   Với a là số thực dương tùy ý, $\sqrt[3]{a^2}$ bằng: 

   A. $a^{\frac{1}{6}}.$

   B. $a^6.$

   C. $a^{\frac{2}{3}}.$

   Đáp án chính xác

   D. $a^{\frac{3}{2}}.$

   Trả lời:

   Chọn C.
   Với một số thực dương ta có: $\sqrt[3]{a^2}=a^{\frac{2}{3}}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tập nghiệm của phương trình log2x2=4 là:
   
   

   Câu hỏi:
   

   Tập nghiệm của phương trình ${\log }_2\left(x^2\right)=4$ là:

   A. $S=\left\{\pm 2\right\}.$

   B. $S=\left\{\sqrt{2}\right\}.$

   C. $S=\left\{\pm 4\right\}.$

   Đáp án chính xác

   D. S = {4}.

   Trả lời:

   Chọn C.
   ĐK: $x^2>0\iff x\ne 0.$
   Ta có: ${\log }_2\left(x^2\right)=4\iff x^2=16\iff \left[\begin{array}{l}x=4\left(n\right)\\ x=-4\left(n\right)\end{array}\right..$
   Suy ra tập nghiệm $S=\left\{-4;4\right\}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho cấp số nhân un có u1=2 và u2=6. Giá trị của u3 là:
   
   

   Câu hỏi:
   

   Cho cấp số nhân $\left(u_n\right)$ có $u_1=2$ và $u_2=6.$ Giá trị của $u_3$ là:

   A. $u_3=10$

   B. $u_3=18$

   Đáp án chính xác

   C. $u_3=14$

   D. $u_3=54$

   Trả lời:

   Chọn B.
   Ta có: $u_1.u_3=u_2^2\Rightarrow u_3=\frac{u_2^2}{u_1}=\frac{6^2}{2}=18.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tiệm cận ngang của đồ thị hàm số y=1−xx+1 có phương trình là:
   
   

   Câu hỏi:
   

   Tiệm cận ngang của đồ thị hàm số $y=\frac{1-x}{x+1}$ có phương trình là:

   A. x = 1

   B. y = 1

   C. y = -1

   Đáp án chính xác

   D. x = -1

   Trả lời:

   Chọn C.
   Ta có: $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{1-x}{x+1}=-1$ (hoặc $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{1-x}{x+1}=-1)$, nên đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số đã cho.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====