Ông A có 200 triệu đồng gửi tiết kiệm tại ngân hàng với kì hạn 1 tháng so với lãi suất 0,6% trên 1 tháng được trả vào cuối kì. Sau mỗi kì hạn ông đến tất toán cả gốc lẫn lãi, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không thay đổi trong quá trình gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông A tất toán và rút ra toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng).

Câu hỏi:

Ông A có 200 triệu đồng gửi tiết kiệm tại ngân hàng với kì hạn 1 tháng so với lãi suất 0,6% trên 1 tháng được trả vào cuối kì. Sau mỗi kì hạn ông đến tất toán cả gốc lẫn lãi, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không thay đổi trong quá trình gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông A tất toán và rút ra toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đồng).

A. 165269 (nghìn đồng).

Đáp án chính xác

B. 169234 (nghìn đồng).

C. 168269 (nghìn đồng).

D. 165288 (nghìn đồng).

Trả lời:

Chọn A.
Bài toán tổng quát:
Gọi a (triệu đồng) là số tiền gửi tiết kiệm, b% là lãi suất trên 1 tháng, c (triệu đồng) là số tiền rút ra mỗi tháng.
* Số tiền ông A còn lại sau kì hạn thứ nhất là:
$S_1=\frac{100+b}{100}.a–c$ (triệu đồng)
* Số tiền ông A còn lại sau kì hạn thứ hai là:
$S_2=\frac{100+b}{100}.S_1–c={\left(\frac{100+b}{100}\right)}^2.a–\frac{100+b}{100}.c–c$ (triệu đồng)
* Số tiền ông A còn lại sau kì hạn thứ ba là:
$S_3=\frac{100+b}{100}.S_2–c={\left(\frac{100+b}{100}\right)}^3.a–{\left(\frac{100+b}{100}\right)}^2.c–\frac{100+b}{100}.c–c$ (triệu đồng)
* Số tiền ông A còn lại sau kì hạn thứ n là:
$S_n=\frac{100+b}{100}.S_{n–1}–c={\left(\frac{100+b}{100}\right)}^n.a–{\left(\frac{100+b}{100}\right)}^{n–1}.c–{\left(\frac{100+b}{100}\right)}^{n–2}.c–...–\frac{100+b}{100}.c–c$
$\Rightarrow S_n={\left(\frac{100+b}{100}\right)}^n.a–c.\left[{\left(\frac{100+b}{100}\right)}^{n–1}+{\left(\frac{100+b}{100}\right)}^{n–2}+...+\frac{100+b}{100}+1\right]$ (triệu đồng)
$\Rightarrow S_n=k^n.a–c.\frac{1–k^n}{1–k}$ (triệu đồng) với $k=\frac{100+b}{100}$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a . Gọi α là góc giữa mặt phẳng (A’BC)  và mặt phẳng (ABC) . Tính tanα.   
   
   

   Câu hỏi:
   

   Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh bằng a . Gọi $\alpha$ là góc giữa mặt phẳng (A’BC)  và mặt phẳng (ABC) . Tính $\tan \alpha .$ 
    

   A. $\tan \alpha =\sqrt{3}.$

   B. $\tan \alpha =2.$

   C. $\tan \alpha =\frac{2\sqrt{3}}{3}.$

   Đáp án chính xác

   D. $\tan \alpha =\frac{\sqrt{3}}{2}.$

   Trả lời:

   Chọn C.

   

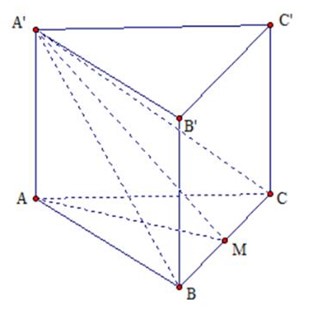
   Gọi M là trung điểm của 
   suy ra $\left\{\begin{array}{l}BC\perp AM\\ BC\perp A‘A\end{array}\right.\Rightarrow BC\perp A‘M.$
   Vậy $\left\{\begin{array}{l}\left(A‘BC\right)\cap \left(ABC\right)=BC\\ BC\perp AM,BC\perp A‘M\end{array} \right.\Rightarrow \alpha =\left(\left(A‘BC\right);\left(ABC\right)\right)=\left(AM;A‘M\right)=\widehat{A‘MA}.$
    

   Tam giác ABC đều cạnh a nên $AM=\frac{a\sqrt{3}}{2}.$
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho các số thực x,y thỏa mãn lny≥lnx3+2−ln3. Tìm giá trị nhỏ nhất của biểu thức H=e4y−x3−x−2−x2+y22+xy+1−y. 
   
   

   Câu hỏi:
   

   Cho các số thực $x,y$ thỏa mãn $\ln y\ge \ln \left(x^3+2\right)-\ln 3.$ Tìm giá trị nhỏ nhất của biểu thức $H=e^{4y-x^3-x-2}-\frac{x^2+y^2}{2}+x\left(y+1\right)-y.$ 

   A. $\frac{1}{e}$

   B. $e.$

   C. 1.

   Đáp án chính xác

   D. 0

   Trả lời:

   Chọn C.
   Điều kiện: $y>\mathrm{0,}x>-\sqrt[3]{2}$
   Từ giả thiết ta có: $\begin{array}{l}\ln y+\ln 3\ge \ln \left(x^3+2\right)\\ \iff \ln 3y\ge \ln \left(x^3+2\right)\\ \iff 3y\ge x^3+2\iff 3\left(y-x\right)\ge x^3-3x+2\end{array}$
   Xét hàm số $h\left(x\right)=x^3-3x+2$ trên  $\left(-\sqrt[3]{2};+\infty \right).$
    

   Ta có: $h‘\left(x\right)=3x^2-\mathrm{3,}h‘\left(x\right)=0\iff 3x^2-3=0\iff \left[\begin{array}{l}x=-1\\ x=1\end{array}\right..$
             $h\left(-1\right)=\mathrm{4,}h\left(1\right)=\mathrm{0,}h\left(-\sqrt[3]{2}\right)=3\sqrt[3]{2}>0.$
   Bảng biến thiên:
   

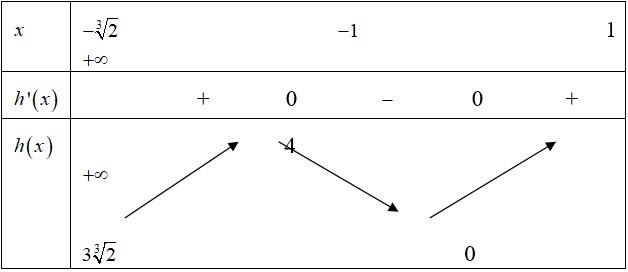
   Từ bảng biến thiên suy ra: $\underset{\left(-\sqrt[3]{2};+\infty \right)}{\min }h\left(x\right)=0.$
   Suy ra: $3\left(y-x\right)\ge 0\iff y-x\ge 0.$
   Ta có:
   $\begin{array}{l}H=e^{4y-x^3-x-2}-\frac{x^2+y^2}{2}+x\left(y+1\right)-y\\ =e^{y-x+3y-\left(x^3+2\right)}-\frac{{\left(y-x\right)}^2}{2}-\left(y-x\right)\ge e^{y-x}-\frac{{\left(y-x\right)}^2}{2}-\left(y-x\right).\end{array}$
   
   Xét hàm số $g\left(t\right)=e^t-\frac{1}{2}{t}^2-t$ trên $\left[0;+\infty \right).$
   Ta có: $g‘\left(t\right)=e^t-t-\mathrm{1,}g“\left(t\right)=e^t-1.$
   Ta có: $\forall t\ge 0\Rightarrow g“\left(t\right)=e^t-1\ge e^0-1=\mathrm{0,}$

   suy ra hàm số $g‘\left(t\right)$ đồng biến trên $\left[0;+\infty \right).$
   Suy ra: $\forall t\ge 0:g‘\left(t\right)\ge g‘\left(0\right)=\mathrm{0,}$
   suy ra hàm số $g\left(t\right)$ đồng biến trên $\left[0;+\infty \right).$
   Vậy $\underset{\left[0;+\infty \right)}{\min }g\left(t\right)=g\left(0\right)=\mathrm{1,}$ Suy ra: $H_{\min }=1.$
   Dấu “=” xảy ra khi và chỉ khi: $\left\{\begin{array}{l}x=y\\ 3y=x^3+2\end{array}\right.\iff x=y=1.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Một đám vi trùng tại ngày thứ t có số lượng là Nt. Biết rằng N’t=20001+2t và lúc đàu đám vi trùng có 300000 con. Ký hiệu L là số lượng vi trùng sau 10 ngày. Tìm L.
   
   

   Câu hỏi:
   

   Một đám vi trùng tại ngày thứ $t$ có số lượng là $N\left(t\right).$ Biết rằng $N‘\left(t\right)=\frac{2000}{1+2t}$ và lúc đàu đám vi trùng có 300000 con. Ký hiệu $L$ là số lượng vi trùng sau 10 ngày. Tìm $L.$

   A. $L=303044.$

   Đáp án chính xác

   B. $L=306089.$

   C. $L=300761.$

   D. $L=301522.$

   Trả lời:

   Chọn A
   Ta có $N‘\left(t\right)=\frac{2000}{1+2t}\Rightarrow N\left(t\right)=\underset{}{\overset{}{\int }}\frac{2000}{1+2t}dt=1000\ln \left(1+2t\right)+C.$
   Lúc đầu đám vi trùng có 300000 con suy ra $N\left(0\right)=300000.$
   Khi đó $1000\ln \left(1+2.0\right)+C=300000\iff C=300000.$
   Suy ra $N\left(t\right)=1000\ln \left(1+2t\right)+300000.$
   Vậy $L=N\left(10\right)=1000\ln 21+300000=303044.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số fx có đạo hàm trên ℝ và có dấu của f'x như sau: Hàm số y=f2−x có bao nhiêu điểm cực trị?
   
   

   Câu hỏi:
   

   Cho hàm số $f\left(x\right)$ có đạo hàm trên $ℝ$ và có dấu của $f‘\left(x\right)$ như sau:

   

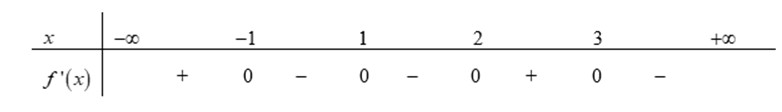
   Hàm số $y=f\left(2-x\right)$ có bao nhiêu điểm cực trị?

   A. 1

   B. 4

   C. 3

   Đáp án chính xác

   D. 2

   Trả lời:

   Chọn C.
   Ta có $y‘=-f‘\left(2-x\right).$ Xét .$y‘=0\iff -f‘\left(2-x\right)=0\iff \left[\begin{array}{l}2-x=-1\\ 2-x=1\\ 2-x=2\\ 2-x=3\end{array}\right.\iff \left[\begin{array}{l}x=3\\ x=1\\ x=0\\ x=-1\end{array}\right.$
   Bảng xét dấu: 
   
   Từ bảng xét dấu, ta suy ra hàm số $y=f\left(2-x\right)$ có tất cả 3 điểm cực trị.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam diện vuông O.ABC có bán kính mặt cầu ngoại tiếp và nội tiếp lần lượt là R và r. Khi đó tỉ số Rr đạt giá trị nhỏ nhất là x+y2. Tính P=x+y.
   
   

   Câu hỏi:
   

   Cho tam diện vuông $O.ABC$ có bán kính mặt cầu ngoại tiếp và nội tiếp lần lượt là $R$ và $r.$ Khi đó tỉ số $\frac{R}{r}$ đạt giá trị nhỏ nhất là $\frac{x+\sqrt{y}}{2}.$ Tính $P=x+y.$

   A. 30.                          

   Đáp án chính xác

   B. 6.                           

   C. 60.    

   D. 27.

   Trả lời:

   Chọn A.
   

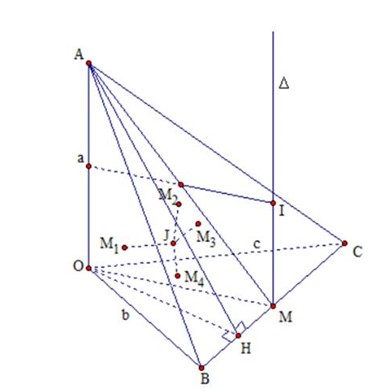
   Đặt $OA=a,OB=b,OC=c.$
   Gọi $M$ là trung điểm của $BC,$ 
   dựng trục đường tròn  ngoại tiếp tam giác $OBC,$
   trên mặt phẳng $\left(OAM\right),$
   kẻ đường trung trực của đoạn $OA$ cắt $\Delta$ tại $I$ là
   tâm mặt cầu ngoại tiếp hình chóp $O.ABC.$
   +) $\begin{array}{l}OM=\frac{1}{2}BC=\frac{1}{2}\sqrt{b^2+c^2},\\ R=\sqrt{M{I}^2+O{M}^2}=\frac{1}{2}\sqrt{a^2+b^2+c^2}.\end{array}$
   +) Gọi $H$ là chân đường cao hạ từ đỉnh $A$ của
    tam giác $ABC,$ suy ra:
   $\left\{\begin{array}{l}BC\perp AH\\ BC\perp AO\end{array}\right.\Rightarrow BC\perp \left(OAH\right)\Rightarrow BC\perp OH.$
   $\begin{array}{l}\frac{1}{O{H}^2}=\frac{1}{b^2}+\frac{1}{c^2}\\ \Rightarrow OH=\frac{bc}{\sqrt{b^2+c^2}}\Rightarrow AH=\sqrt{O{A}^2+O{H}^2}\\ =\sqrt{a^2+\frac{b^2{c}^2}{b^2+c^2}}=\sqrt{\frac{a^2{b}^2+a^2{c}^2+b^2{c}^2}{\sqrt{b^2+c^2}}}\end{array}$

    
   Suy ra:$\begin{array}{l}{S}_{\Delta ABC}=\frac{1}{2}AH.BC=\frac{1}{2}\frac{\sqrt{a^2{b}^2+a^2{c}^2+b^2{c}^2}}{\sqrt{b^2+c^2}}.\sqrt{b^2+c^2}\\ =\frac{1}{2}\sqrt{a^2{b}^2+a^2{c}^2+b^2{c}^2}.\end{array}$

    
   +) Gọi $J$ là tâm mặt cầu nội tiếp hình chóp $O.ABC.$
   Khi đó:
    $\begin{array}{l}d\left(J;\left(OAB\right)\right)=d\left(J;\left(OBC\right)\right)\\ =d\left(J;\left(OAC\right)\right)=d\left(J;\left(ABC\right)\right)=r.\end{array}$
   $\begin{array}{l}{V}_{O.ABC}=V_{J.ABC}+V_{J.OBC}+V_{J.AOC}+V_{J.ABO}\\ \iff \frac{1}{6}abc=\frac{1}{3}r\left(S_{\Delta ABC}+S_{\Delta OBC}+S_{\Delta AOC}+S_{\Delta ABO}\right)\end{array}$
       
    $\iff \frac{1}{2}abc=r\left(\frac{1}{2}\sqrt{a^2{b}^2+a^2{c}^2+b^2{c}^2}+\frac{1}{2}\left(ab+bc+ca\right)\right).$
        $\iff \frac{1}{r}=\frac{1}{abc}\left(\sqrt{a^2{b}^2+a^2{c}^2+b^2{c}^2}+ab+bc+ca\right).$
   Suy ra:
    $\frac{R}{r}=\frac{1}{2}.\frac{1}{abc}.\sqrt{a^2+b^2+c^2}\left(\sqrt{a^2{b}^2+a^2{c}^2+b^2{c}^2}+ab+bc+ca\right)$
                  $\ge \frac{1}{2}.\frac{1}{abc}.\sqrt{3\sqrt[3]{a^2{b}^2{c}^2}}\left(\sqrt{3\sqrt[3]{a^2{b}^2.a^2{c}^2.b^2{c}^2}}+3\sqrt[3]{ab.bc.ca}\right)$
          $=\frac{1}{2}.\frac{1}{abc}.\sqrt{3}.\sqrt[3]{abc}\left(\sqrt{3}.\sqrt[3]{a^2{b}^2{c}^2}+3\sqrt[3]{a^2{b}^2{c}^2}\right)=\frac{3+3\sqrt{3}}{2}=\frac{3+\sqrt{27}}{2}.$
   Vậy $P=a+b=30.$ Dấu “=” xảy ra khi $a=b=c$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====