Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd¯ , trong đó 1≤a≤b≤c≤d≤9 .

Câu hỏi:

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng $\overline{abcd}$ , trong đó $1\le a\le b\le c\le d\le 9$ .

A. 0,079.

B. 0,055.

Đáp án chính xác

C. 0,014.

D. 0,0495.

Trả lời:

Đáp án B
Không gian mẫu: $n\left(\Omega \right)={9.10}^3=9000.$
Gọi A là biến cố: “số được chọn có dạng $\overline{abcd}$ , trong đó ”$1\le a\le b\le c\le d\le 9$.
TH1: $1\le a=b<c<d\le 9$
Chọn ngẫu nhiên 4 số trong các số từ 1 đến 9 có $C_9^4=126$  cách.
Có duy nhất một cách xếp các chữ số a, b, c, d theo thứ tự tăng dần, do đó trường hợp này có 126 số thỏa mãn.
TH2: $1\le a=b<c<d\le 9$ . Số cần tìm có dạng $\overline{aacd}$ .
Chọn ngẫu nhiên 3 số trong các số từ 1 đến 9 có $C_9^3=84$  cách.
Có duy nhất một cách xếp các chữ số a, c, d theo thứ tự tăng dần, do đó trường hợp này có 84 số thỏa mãn.
Tương tự như vậy, các trường hợp $1\le a<b=c<d\le \mathrm{9,}1\le a<b<c=d\le 9$ , mỗi trường hợp cũng có 84 số thỏa mãn.
TH3: $1\le a=b=c<d\le 9$ . Số cần tìm có dạng $\overline{aaad}$ .
Chọn ngẫu nhiên 2 số trong các số từ 1 đến 9 có $C_9^2=36$  cách.
Có duy nhất một cách xếp các chữ số a, d theo thứ tự tăng dần, do đó trường hợp này có 36 số thỏa mãn.
Tương tự như vậy, các trường hợp $1\le a=b<c=d\le \mathrm{9,}1\le a<b=c=d\le 9$ , mỗi trường hợp cũng có 36 số thỏa mãn.
TH4: $1\le a=b=c=d\le 9$ . Số cần tìm có dạng $\overline{aaaa}$ .
Có 9 số thỏa mãn $\Rightarrow n\left(A\right)=126+3.84+3.36+9=495$ .
Vậy $P\left(A\right)=\frac{495}{9000}=\mathrm{0,055}$ .

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0), B(0;0;2), C(0;-3;0) . Bán kính mặt cầu ngoại tiếp tứ diện OABC là:
   
   

   Câu hỏi:
   

   Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0), B(0;0;2), C(0;-3;0) . Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

   A. $\frac{\sqrt{14}}{4}.$

   B. $\sqrt{14}.$

   C. $\frac{\sqrt{14}}{3}.$

   D. $\frac{\sqrt{4}}{2}.$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   
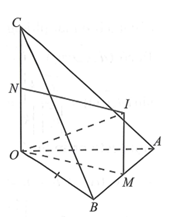
   Tứ diện OABC có OA, OB, OC đôi một vuông góc.
   Gọi M, N lần lượt là trung điểm của AB và OC.
   Ta có: $\left\{\begin{array}{l}OC\perp OA\\ OC\perp OB\end{array}\right.\Rightarrow OC\perp \left(OAB\right)$ .
   Qua M dựng đường thẳng song song với OC, qua N dựng đường thẳng song song với OM. Hai đường thẳng này cắt nhau tại I.
   $\Delta OAB$ vuông tại $O\Rightarrow M$  là tâm đường tròn ngoại tiếp $\Delta OAB\Rightarrow IO=IA=IB.$
   $I\in IN\Rightarrow IO=IC\Rightarrow IO=IA=IB=IC\Rightarrow I$
    là tâm mặt cầu ngoại tiếp O.ABC.
   Ta có: $OA=\mathrm{1,}OB=\mathrm{2,}OC=3\Rightarrow OM=\frac{1}{2}AB=\frac{1}{2}\sqrt{1^2+2^2}=\frac{\sqrt{5}}{2}$ $R=OI=\sqrt{I{M}^2+O{M}^2}=\sqrt{\frac{9}{4}+\frac{5}{4}}=\frac{\sqrt{14}}{2}$.
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho cấp số cộng un  có u1=11  và công sai d=4 . Hãy tính u99 .
   
   

   Câu hỏi:
   

   Cho cấp số cộng $\left(u_n\right)$  có $u_1=11$  và công sai $d=4$ . Hãy tính $u_{99}$ .

   A. 401.

   B. 404.

   C. 403.       

   Đáp án chính xác

   D. 402.

   Trả lời:

   Đáp án C
   Ta có: $u_1=11;d=4\Rightarrow u_{99}=u_1+\left(99-1\right).d=11+98.4=403$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tìm a để hàm số fx=x2−1x−1 khi x≠1a        khi x=1  liên tục tại điểm x0=1 .
   
   

   Câu hỏi:
   

   Tìm a để hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2-1}{x-1}khix\ne 1\\ akhix=1\end{array}\right.$  liên tục tại điểm $x_0=1$ .

   A. $a=0.$

   B. $a=-1.$

   C. $a=2.$

   Đáp án chính xác

   D. $a=1.$

   Trả lời:

   Đáp án C
   Hàm số $y=f\left(x\right)$  liên tục tại $x=1\Rightarrow \lim x\to 1f\left(x\right)=f\left(1\right)=a$

   $\iff \lim x\to 1\frac{x^2-1}{x-1}=a\iff \lim x\to 1\frac{\left(x-1\right)\left(x+1\right)}{x-1}=a\iff \lim x\to 1\left(x+1\right)=a\iff 2=a.$Định nghĩa: Cho hàm số $y=f\left(x\right)$  xác định trên khoảng K và $x_0\in K$ . Hàm số $y=f\left(x\right)$  được gọi là hàm số liên tục tại $x_0$  nếu $\lim x\to x_{0}f\left(x\right)=f\left(x_0\right)$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA⊥ABCD, AB=BC=a, AD=2a, SA=a2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.
   
   

   Câu hỏi:
   

   Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết $SA\perp \left(ABCD\right),AB=BC=a,AD=2a,SA=a\sqrt{2}$ . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.

   A. $\frac{a\sqrt{3}}{2}.$

   B. a.

   Đáp án chính xác

   C. $\frac{a\sqrt{6}}{3}.$

   D. $\frac{a\sqrt{30}}{6}.$

   Trả lời:

   Đáp án B
   
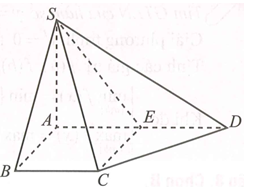
   Xét tứ giác ABCE có $AE//BC,AE=BC=a\Rightarrow ABCE$  là hình bình hành.
   Lại có $\widehat{ABC}=90°$  (giả thiết), $AC=BC\Rightarrow ABCE$  là hình vuông cạnh a.
   Bán kính đường tròn ngoại tiếp hình vuông ABCE là $R_d=\frac{a\sqrt{2}}{2}$ .
   Sử dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp chóp S.ABCE là: $R=\sqrt{\frac{S{A}^2}{4}+R_d^2}=\sqrt{\frac{2a^2}{4}+\frac{2a^2}{4}}=a$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Gọi  là nghiệm dương nhỏ nhất của phương trình 3sin2x+2sinxcosx−cos2x=0 . Chọn khẳng định đúng?
   
   

   Câu hỏi:
   

   Gọi  là nghiệm dương nhỏ nhất của phương trình $3{\sin }^{2}x+2\sin x\cos x-{\cos }^{2}x=0$ . Chọn khẳng định đúng?

   A. $x_0\in \left(\frac{\pi }{2};\pi \right).$

   B. $x_0\in \left(\frac{3\pi }{2};2\pi \right).$

   C. $x_0\in \left(0;\frac{\pi }{2}\right).$

   Đáp án chính xác

   D. $x_0\in \left(\pi ;\frac{3\pi }{2}\right).$

   Trả lời:

   Đáp án C                                    
   Với $\cos x=0\iff {\sin }^{2}x=1$  không phải là nghiệm của phương trình.
   Với $\cos x\ne 0$
   Phương trình tương đương với: $\begin{array}{l}3{\sin }^{2}x+2\sin x\cos x-{\cos }^{2}x=0\iff 3\frac{{\sin }^{2}x}{{\cos }^{2}x}+2\frac{\sin x}{\cos x}-1=0\\ \iff 3{\tan }^{2}x+2\tan x-1=0\iff \left[\begin{array}{l}\tan x=-1\\ \tan x=\frac{1}{3}\end{array}\right.\iff \left[\begin{array}{l}x=-\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\\ x=\arctan \frac{1}{3}+k\pi ,k\in \mathbb{Z}\end{array}\right..\end{array}$
   Nghiệm nguyên dương nhỏ nhất của phương trình là $x=\arctan \frac{1}{3}\in \left(0;\frac{\pi }{2}\right)$ .

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====