Chuyên đề đường tiệm cận của đồ thị hàm số

Chuyên đề đường tiệm cận của đồ thị hàm số

Bài 5. Đường tiệm cận

A. Lý thuyết về đường tiệm cận ngang của đồ thị hàm số

1. Định nghĩa

Định nghĩa: Cho hàm số \[y = f(x)\] xác định trên một khoảng vô hạn (là khoảng dạng \[(a; + \infty )\], \[( – \infty ;b)\]hoặc \[( – \infty ; + \infty )\]. Đường thằng y = y₀ là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số \[y = f(x)\] nếu ít nhất một trong các điều kiện sau được thỏa mãn

\[\mathop {\lim }\limits_{x \to  + \infty } f(x) = {y_0};\mathop {\lim }\limits_{x \to  – \infty } f(x) = {y_0}\].

2. Kết luận về tiệm cận ngang của đồ thị hàm phân thức

Đặt \[f(x) = \frac{{p(x)}}{{q(x)}}\]là một hàm phân thức, trong đó \[p(x)\]và \[q(x)\]là các hàm đa thức.

Nếu bậc của tử thức \[p(x)\]nhỏ hơn bậc của mẫu thức \[q(x)\], thì y = 0 là một tiệm cận ngang của đồ thị hàm số \[y = f(x)\].

Nếu bậc của tử thức \[p(x)\]bằng bậc của mẫu thức \[q(x)\], thì \[y = \frac{a}{b}\] là một tiệm cận ngang của đồ thị hàm số \[y = f(x)\], trong đó a, b lần lượt là hệ số của hạng tử có bậc cao nhất của đa thức tử là\[p(x)\] và đa thức mẫu số \[q(x)\].

Nếu bậc của tử thức \[p(x)\]lớn hơn bậc của mẫu thức \[q(x)\], thì hàm số \[y = f(x)\] không có tiệm cận ngang.

3. Một số lưu ý về các giới hạn đặc biệt

\[\mathop {\lim }\limits_{x \to  \pm \infty } c = c;\]

\[\mathop {\lim }\limits_{x \to  \pm \infty } \frac{c}{{{x^k}}} = 0;\] (c là hằng số, k nguyên dương);

\[\mathop {\lim }\limits_{x \to  + \infty } {x^k} =  + \infty \] với k nguyên dương;

\[\mathop {\lim }\limits_{x \to  – \infty } {x^k} =  – \infty \], nếu k là số nguyên lẻ;

\[\mathop {\lim }\limits_{x \to  – \infty } {x^k} =  + \infty \], nếu k là số nguyên chẵn.

Với bài toán cần tìm giới hạn của hàm số tại vô cực ta sẽ sử dụng chức năng CALC để tính các giá trị của \[f(x)\] tại các giá trị x rất lớn.

Để tính \[\mathop {\lim }\limits_{x \to  + \infty } f(x)\] thì ta nhập hàm số\[f(x)\] vào màn hình và sử dụng CALC để tính giá trị của hàm số tại x = 10¹⁰.

Để tính \[\mathop {\lim }\limits_{x \to  – \infty } f(x)\] thì ta nhập hàm số\[f(x)\] vào màn hình và sử dụng CALC để tính giá trị của hàm số tại x = – 10¹⁰.

Ví dụ 1. \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{2017}}{{3{x^3} – 5{x^5}}}\] bằng:

A. \[\frac{{2017}}{3}.\]

B. \[ – \infty \].

C. \[ + \infty \].

D. 0.

Hướng dẫn giải

Đáp án D

Sử dụng MTCT tính giá trị hàm số tại x = 10¹⁰ ta được kết quả như hình bên.

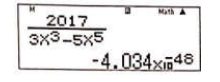
Đó là kết quả rất gần 0.

Ví dụ 2. Tìm tiệm cận ngang của đồ thị hàm số \[y = \frac{{2x + 3}}{{5x + 6}}.\]

Lời giải

Hàm số đã cho xác định trên\[\left( { – \infty ; – \frac{6}{5}} \right) \cup \left( { – \frac{6}{5}; + \infty } \right).\]

Ta có\[\mathop {\lim }\limits_{x \to  – \infty } \frac{{2x + 3}}{{5x + 6}} = \frac{2}{5}\]; \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x + 3}}{{5x + 6}} = \frac{2}{5}\].

Vậy đồ thị hàm số đã cho có một tiệm cận ngang \[y = \frac{2}{5}\].

Với bài toán này, ta không cần thiết phải sử dụng máy tính cầm tay, mà chỉ cần nhớ tính chất.

Đồ thị hàm phân thức có dạng \[y = \frac{{ax + b}}{{cx + d}},(c \ne 0,ad – bc \ne 0)\] luôn có một tiệm cận ngang \[y = \frac{a}{c}\] và một tiệm cận đứng \[y =  – \frac{d}{c}\].

Ví dụ 3. Tìm tiệm cận ngang của đồ thị hàm số \[y = 5 – \frac{2}{{{x^2}}}\].

Hướng dẫn giải

Tập xác định \[D = R\backslash \{ 0\} \].

Cách 1. \[\mathop {\lim }\limits_{x \to  \pm \infty } \left( {5 – \frac{2}{{{x^2}}}} \right) = \mathop {\lim }\limits_{x \to  \pm \infty } 5 – \mathop {\lim }\limits_{x \to  \pm \infty } \frac{2}{{{x^2}}} = 5 – 2.0 = 5\]

Vậy đồ thị hàm số đã cho có một tiệm cận ngang là y = 5.

Cách 2. Từ kết luận về tiệm cận ngang của hàm phân thức phía trên ta thấy \[y = 5 – \frac{2}{{{x^2}}} = \frac{{5{x^2} – 2}}{{{x^2}}}\]. Do hàm số là hàm phân thức có bậc tử bằng bậc mẫu nên đồ thị hàm số có tiệm cận ngang là \[y = \frac{5}{1} = 5\].

Cách 3. Sử dụng máy tính cầm tay.

Nhập vào màn hình hàm số và CALCx = 10¹⁰ thì ta có màn hình hiện như hình bên. Từ đây kết luận đồ thị hàm số có đường tiệm cận ngang y = 5.

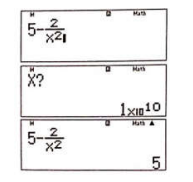
Ví dụ 4. Tìm tiệm cận ngang của đồ thị hàm số

a. \[y = \frac{{ – 2x + 3}}{{3{x^2} + 1}}\]

b. \[y = \frac{{ – 2{x^2} + 3}}{{3{x^2} + 1}}\]

c. \[y = \frac{{ – 2{x^3} + 3}}{{3{x^2} + 1}}\]

Hướng dẫn giải

a. Vì bậc của đa thức tử nhỏ hơn bậc của đa thức mẫu số nên y = 0 là tiệm cận ngang của đồ thị hàm số đã cho.

b. Vì bậc của đa thức tử bằng bậc của đa thức mẫu số nên đường thẳng \[y = \frac{{ – 2}}{3}\] là tiệm cận ngang của đồ thị hàm số đã cho.

c. Vì bậc của đa thức tử lớn hơn bậc của đa thức mẫu số nên đồ thị hàm số không có tiệm cận ngang.

B. Lý thuyết về đường tiệm cận đứng của đồ thị hàm số

1. Định nghĩa

Định nghĩa: Đường thẳng x = x₀ được gọi là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số \[y = f(x)\] nếu ít nhất một trong các điều kiện sau được thỏa mãn

\[\mathop {\lim }\limits_{x \to x_0^ + } f(x) =  + \infty ,\mathop {\lim }\limits_{x \to x_0^ – } f(x) =  – \infty \]

\[\mathop {\lim }\limits_{x \to x_0^ + } f(x) =  – \infty ,\mathop {\lim }\limits_{x \to x_0^ – } f(x) =  + \infty \]

Nếu c là một số thức thỏa mãn \[q(c) = 0\] và \[q(c) \ne 0\], thì đồ thị hàm số \[y = \frac{{p(x)}}{{q(x)}}\] có tiệm cận đứng x = c.

2. Kĩ năng sử dụng máy tính cầm tay để tìm tiệm cận đứng của đồ thị hàm số

Để tìm giới hạn của hàm số tại một điểm,  ta sử dụng máy tính cầm tay như sau:

Để tính \[\mathop {\lim }\limits_{x \to {a^ + }} f(x)\] thì ta nhập hàm số\[f(x)\]vào màn hình, sử dụng lệnh CALC và gán \[x = a + {10^{ – 9}}\].

Để tính \[\mathop {\lim }\limits_{x \to {a^ + }} f(x)\] thì ta nhập hàm số\[f(x)\]vào màn hình, sử dụng lệnh CALC và gán \[x = a – {10^{ – 9}}\].

Ví dụ 5. Số tiệm cận của đồ thị hàm số \[y = \frac{x}{{{x^2} – 1}}\] là:

A. 1

B. 2

C. 4

D.3

Hướng dẫn giải

Đáp án D.

Tập xác định : \[D = R\backslash \{ 1\} \]

Nhận thấy bậc của đa thức tử số nhỏ hơn bậc của đa thức mẫu số nên y = 0 là tiệm cận ngang của đồ thị hàm số.

Ta có \[{x^2} – 1 = 0 \Leftrightarrow x =  – 1;x = 1\] (thỏa mãn không là nghiệm của đa thức tử số), do đó \[x = 1;x =  – 1\]lần lượt là hai đường tiệm cận đứng của đồ thị hàm số đã cho.

Ví dụ 6. Cho hàm số \[y = \frac{7}{{2x + 5}}\]. Số tiệm cận của đồ thị hàm số bằng

A. 2.

B. 3.

C. 1.

D. 0.

Hướng dẫn giải

Đáp án A

TXĐ: \[D = R\backslash \{  – \frac{5}{2}\} \]. Theo chú ý thì ta thấy đồ thị hàm số có một tiệm cận đứng \[x =  – \frac{5}{2}\] và một tiệm cận ngang là \[y = \frac{0}{2} = 0\].

Ví dụ 7. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số \[y = \frac{{x – 2}}{{{x^2} + mx + m}}\] có đúng một tiệm cận đứng.

A. Không có giá trị thực nào của tham số m thỏa mãn yêu cầu đề bài.

B. \[0 \le m \le 4\] hoặc \[m =  – \frac{4}{3}\].

C. \[m \in \left\{ {0;4; – \frac{4}{3}} \right\}\].

D. \[m \le 0\] hoặc \[m \ge 4\].

Hướng dẫn giải

Đáp án C

Ta thấy đây là hàm phân thức nên ta có thể áp dụng các chú ý đưa ra ở phần lý thuyết về tiệm cận đứng và tiệm cận ngang.

Để đồ thị hàm số có đúng một tiệm cận đứng thì phương trình \[{x^2} + mx + m = 0\].

TH1: có duy nhất một nghiệm khác 2

\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} – 4m = 0}\\{4 + 3m \ne 0}\end{array}} \right. \Rightarrow m = 0;m = 4.\]

TH2: có một nghiệm bằng 2, một nghiệm khác

 \[ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{m^2} – 4m \ne 0}\\{{2^2} + 2m + m = 0}\end{array}} \right. \Leftrightarrow m =  – \frac{4}{3}.\]

 Ví dụ 8. Cho hàm số\[y = f(x)\] có \[\mathop {\lim }\limits_{x \to  + \infty } f(x) = 2,\mathop {\lim }\limits_{x \to  – \infty } f(x) =  + \infty \]. Khẳng định nào sau đây là đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.

B. Đồ thị hàm số đã cho có hai tiệm cận ngang phân biệt.

C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng x = 2.

D. Đồ thị hàm số đã cho không có tiệm cận ngang.

Hướng dẫn giải

Đáp án A

Áp dụng định nghĩa về tiệm cận ngang ta suy ra được A là đáp án đúng.

Ví dụ 9. Tìm số tiệm cận đứng của đồ thị hàm số \[y = \frac{{{x^2} – 3x – 4}}{{{x^2} – 16}}\].

A. 2.

B. 3.

C. 1.

D. 0.

Hướng dẫn giải

Đáp án C

Ta có. \[y = \frac{{{x^2} – 3x – 4}}{{{x^2} – 16}} = \frac{{(x + 1)(x – 4)}}{{(x – 4)(x + 4)}} = \frac{{x + 1}}{{x + 4}}\].

Vậy đồ thị hàm số có duy nhất một tiệm cận đứng là đường thẳng x = -4.

Ví dụ 10. Tìm tất cả các giá trị thực của hàm số m sao cho đồ thị hàm số \[y = \frac{{2x – \sqrt {m{x^2} + 1} }}{{x – 1}}\] có đúng hai tiệm cận ngang.

A. m < 0.

B. 0 < m < 3 hoặc m > 3.

C. m > 0.

D. m = 0.

Hướng dẫn giải

Đáp án C

Để đồ thị hàm số có đường tiệm cận đứng thì \[m \ne  – \frac{5}{4}\] (Nếu \[m =  – \frac{5}{4}\] thì \[y = 1 \Rightarrow \] đồ thị hàm số không có tiệm cận đứng).

Khi đó, áp dụng chú ý ở trên thì đồ thị hàm số đã cho luôn có một tiệm cận đứng là x = m. Do vậy để tiệm cận đứng nằm bên phải trục Oy thì m > 0 và \[m \ne  – \frac{5}{4}\].

Ghi nhớ

Tìm nghiệm của phương trình mẫu.

Xem các nghiệm đó có phải là nghiệm của tử số không (bằng cách thay hoặc thử trực tiếp).

Kết luận.

Ví dụ 11. Tìm tất cả các tiệm cận đứng của đồ thị hàm số\[y = \frac{{2x – 1 – \sqrt {{x^2} + x + 3} }}{{{x^2} – 5x + 6}}\]

A. x = 3 và x = -2.

B. x = -3.

C. x = 3 và x = 2.

D. x = 3.

 

 

 

Xem thêm