Giải SBT Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Bài 1.1 trang 7 SBT Giải tích 12: Xét sự đồng biến, nghịch biến của các hàm số:
a)
b)
c)
d)
Phương pháp giải:
– Tính .
– Tìm nghiệm của phương trình .
– Xét dấu và kết luận.
Lời giải:
a)
TXĐ: R
Xét dấu :
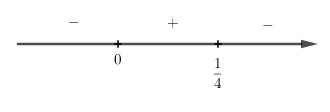
Ta thấy, nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên các khoảng và .
b)
TXĐ: R
Bảng biến thiên:
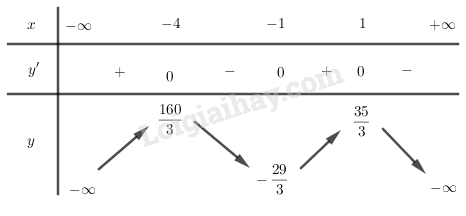
Vậy hàm số đã cho đồng biến trên các khoảng và , nghịch biến trên các khoảng và .
c)
TXĐ: R
y’=0 <=>
nên hàm số đồng biến trên các khoảng và .
nên hàm số nghịch biến trên khoảng .
d)
TXĐ: R
nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên khoảng .
Bài 1.2 trang 7 SBT Giải tích 12: Tìm các khoảng đồng biến, nghịch biến của các hàm số:
a)
b)
c)
d)
e)
g)
Phương pháp giải:
a) – Tìm TXĐ.
– Tính theo công thức
– Xét dấu và kết luận khoảng đồng biến, nghịch biến.
b) – Tìm TXĐ.
– Tính theo công thức
– Xét dấu và kết luận khoảng đồng biến, nghịch biến.
c) – Tìm TXĐ.
– Tính theo công thức
– Xét dấu và kết luận khoảng đồng biến, nghịch biến.
d) – Tìm TXĐ.
– Tính theo công thức .
– Xét dấu và kết luận khoảng đồng biến, nghịch biến.
e) – Tìm TXĐ.
– Tính theo công thức .
– Xét dấu và kết luận khoảng đồng biến, nghịch biến.
Lời giải:
a)
TXĐ:
Vậy hàm số nghịch biến trên các khoảng và .
b)
TXĐ:
Ta có:
nên hàm số đồng biến trên khoảng .
nên hàm số nghịch biến trên khoảng .
c)
TXĐ:
Vậy hàm số nghịch biến trên các khoảng .
d)
TXĐ: .
Ta có:
.
Bảng biến thiên:
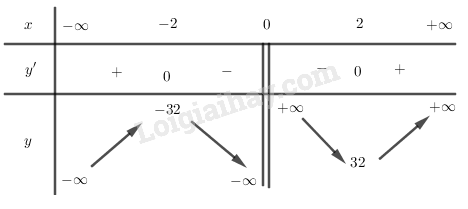
Vậy hàm số đồng biến trên các khoảng và .
Hàm số nghịch biến trên các khoảng và .
e)
TXĐ:
Ta có:
Khi đó
Bảng biến thiên:
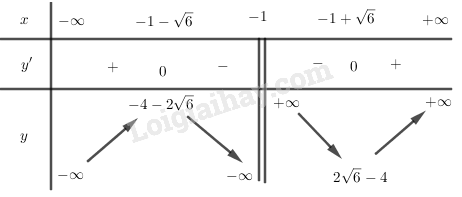
Vậy hàm số đã cho đồng biến trên các khoảng
và nghịch biến trên các khoảng
g)
TXĐ:
Ta có: .
Vậy hàm số đồng biến trên các khoảng và .
Bài 1.3 trang 8 SBT Giải tích 12: Xét tính đơn điệu của các hàm số:
a)
b)
Phương pháp giải:
– Tìm tập xác định.
– Tính và tìm nghiệm của .
– Xét dấu của và kết luận khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a)
Ta có:
.
Bảng biến thiên:
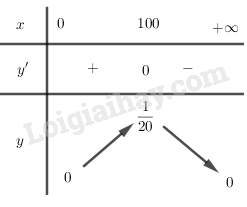
Vậy hàm số đồng biến trên khoảng và nghịch biến trên khoảng
b)
TXĐ:
;
Bảng biến thiên:
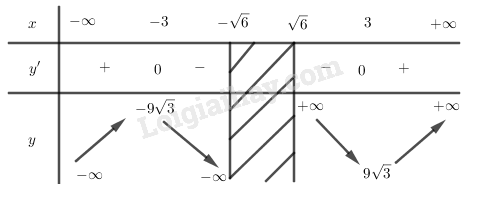
Vậy hàm số đồng biến trên các khoảng , nghịch biến trên các khoảng .
Bài 1.4 trang 8 SBT Giải tích 12: Xét sự đồng biến, nghịch biến của các hàm số:
a)
b) ,
Phương pháp giải:
– Tìm TXĐ.
– Tính và xét dấu .
– Kết luận.
Lời giải:
a)
.
với mọi
Dấu “=” xảy ra chỉ tại và .
Vậy hàm số đồng biến trên đoạn .
b) ,
Xét hàm số với .
Với ta có:
⟺ < 0
⟺ ,k = 0, 1, 2 ….
⟺ , k = 0, 1, 2 ……..
Do đó, hàm số đồng biến trên các khoảng
và nghịch biến trên các khoảng
……,
với k = 0, 1, 2 …
Bài 1.5 trang 8 SBT Giải tích 12: Xác định để hàm số sau:
a) đồng biến trên từng khoảng xác định;
b) nghịch biến trên
Phương pháp giải:
a) – Tìm TXĐ .
– Hàm số phân thức bậc nhất trên bậc nhất đồng biến trên nếu .
b) – Hàm số đa thức bậc ba nghịch biến trên nếu .
– Tam thức bậc hai
Lời giải:
a) đồng biến trên từng khoảng xác định;
Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng xác định
b) nghịch biến trên
Tập xác định:
Hàm số nghịch biến trên R
Bài 1.6 trang 8 SBT Giải tích 12: Chứng minh phương trình sau có nghiệm duy nhất
Phương pháp giải:
Sử dụng phương pháp hàm số:
– Xét hàm số vế trái và chứng minh nó đơn điệu trên .
– Từ đó suy ra phương trình có nghiệm duy nhất.
Lời giải:
Đặt
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: và .
Hàm số đồng biến trên R và có một nghiệm
Vậy phương trình đã cho có một nghiệm duy nhất.
Bài 1.7 trang 8 SBT Giải tích 12: Chứng minh các bất đẳng thức sau:
a) ,
b) với
Phương pháp giải:
a) Xét hàm và chứng minh nó đồng biến trên .
Từ đó suy ra điều phải chứng minh.
b) Xét các hàm số và trên và chứng minh chúng nghịch biến trên .
Từ đó suy ra điều phải chứng minh.
Lời giải:
a) ,
Xét hàm trên khoảng ta có:
với vì với mọi nên
Do đó hàm số đồng biến trên
với mọi .
b) với
Xét trên ta có: .
Vì nên nên hàm số nghịch biến trên
Do đó
Xét trên ta có:
Vì nên hay nghịch biến trên
Do đó hay
Từ và ta được với . (đpcm)
Bài 1.8 trang 8 SBT Giải tích 12: Xác định giá trị của b để hàm số nghịch biến trên toàn trục số.
Phương pháp giải:
Hàm số nghịch biến trên với mọi nếu f ′ ( x ) ≤ 0 , ∀ x ∈ D .
Lời giải:
nghịch biến trên R nếu ta có:
.
Vì nên
Bài 1.9 trang 8 SBT Giải tích 12: Khẳng định nào sau đây là đúng?
A. là hàm số chẵn.
B. Hàm số xác định trên .
C. Hàm số đồng biến trên .
D. Hàm số nghịch biến trên .
Phương pháp giải:
Xét tính đúng sai của mỗi đáp án, sử dụng tính chẵn lẻ, tính đơn điệu của hàm số.
Lời giải:
Đáp án A: TXĐ: .
Có nên hàm số lẻ trên .
A sai.
Đáp án B: ĐKXĐ: nên TXĐ: .
B sai.
Đáp án C: TXĐ:
Có nên hàm số đồng biến trên .
C đúng.
Chọn C.
Chú ý:
Ngoài ra các em cũng có thể kiểm tra thêm đáp án D: nên hàm số đồng biến trên . Do đó D sai.
Bài 1.10 trang 8 SBT Giải tích 12: Hàm số nghịch biến trên khoảng:
A.
B.
C.
D.
Phương pháp giải:
– Tìm TXĐ .
– Tính và tìm nghiệm của trên .
– Xét dấu và suy ra khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
TXĐ: .
Ta có: .
Bảng biến thiên:
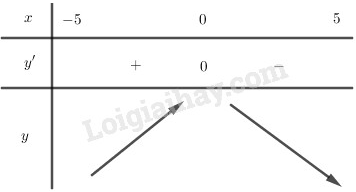
Hàm số đã cho nghịch biến trên .
Chọn C.
Bài 1.11 trang 8 SBT Giải tích 12: Hàm số đồng biến trên khoảng
A.
B.
C.
D.
Phương pháp giải:
– Tìm TXĐ .
– Tính và tìm nghiệm của trên .
– Xét dấu và suy ra khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
TXĐ: .
Có
Do đó hàm số đồng biến trên .
Chọn B.
Bài 1.12 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên thì phương trình có nghiệm duy nhất.
Lời giải:
Đáp án C vì: Xét hàm có .
và nên hàm số đồng biến trên .
Mặt khác nên .
Hàm số liên tục trên nên tồn tại để hay phương trình có nghiệm duy nhất trên .
Chọn C.
Chú ý:
Cách khác:
+) Phương trình (vô nghiệm vì ) nên loại A.
+) Các phương trình và có nhiều hơn một nghiệm nên loại B, D.
Chọn C.
Bài 1.13 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên thì phương trình có nghiệm duy nhất.
Lời giải chi tiết:
Đáp án B vì: Xét hàm có nên hàm số đồng biến trên .
Mặt khác, nên phương trình có nghiệm duy nhất trên .
Chọn B.
Bài 1.14 trang 8 SBT Giải tích 12: Phương trình nào sau đây có nghiệm duy nhất trên ?
A.
B.
C.
D.
Phương pháp giải:
Loại đáp án, xét các đáp án bằng cách giải mỗi phương trình và suy ra số nghiệm.
Lời giải chi tiết:
Đáp án A: nên phương trình có nghiệm.
Đáp án B: Xét hàm có và nên hay hàm số nghịch biến trên .
Mà nên , hàm số liên tục trên nên phương trình có nghiệm .
Kết hợp với hàm số nghịch biến trên nên phương trình đã cho có nghiệm duy nhất trên .
Chọn B.
Bài 1.15 trang 8 SBT Giải tích 12: Tìm giá trị của tham số để hàm số đồng biến trên .
A.
B.
C.
D.
Phương pháp giải:
– Tính .
– Hàm số đồng biến trên .
Lời giải chi tiết:
TXĐ: .
Ta có: .
Hàm số đồng biến trên
.
Chọn D.
Bài 1.16 trang 8 SBT Giải tích 12: Tìm giá trị của tham số để hàm số nghịch biến trên từng khoảng xác định.
A. hoặc
B.
C.
D.
Phương pháp giải:
– Tính .
– Hàm số nghịch biến trên từng khoảng xác định nếu trên từng khoảng xác định.
Lời giải chi tiết:
TXĐ: .
Ta có: .
Hàm số nghịch biến trên từng khoảng và nếu .
Chọn A.