Tài liệu Tìm khoảng đồng biến, nghịch biến bằng bảng biến thiên và đồ thị hàm số gồm các nội dung sau:
A. Phương pháp giải
– Tóm tắt ngắn gọn phương pháp Tìm khoảng đồng biến, nghịch biến bằng bảng biến thiên và đồ thị hàm số
B. Bài tập
– Gồm 9 câu hỏi trắc nghiệm giúp học sinh rèn luyện cách giải các bài tập Tìm khoảng đồng biến, nghịch biến bằng bảng biến thiên và đồ thị hàm số
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

TÌM KHOẢNG ĐƠN ĐIỆU CỦA HÀM SỐ DỰA VÀO BẢNG BIẾN THIÊN VÀ ĐỒ THỊ
A. PHƯƠNG PHÁP GIẢI
– Quan sát bảng biến thiên
+ Nếu dấu của là dương thì hàm số đồng biến trên khoảng đó.
+ Nếu dấu của là âm thì hàm số nghịch biến trên khoảng đó.
– Quan sát đồ thị hàm số
+ Nếu đầu bài cho đồ thị hàm số f(x)
Khoảng giá trị của x làm cho hàm số f(x) đi lên là đồng biến.
Khoảng giá trị của x làm cho hàm số f(x) đi xuống là nghịch biến.
+ Nếu đầu bài cho đồ thị hàm số f'(x)
Khoảng giá trị của x làm cho hàm số f'(x) nằm bên trên trục hoành là đồng biến.
Khoảng giá trị của x làm cho hàm số f'(x) nằm bên dưới trục hoành là nghịch biến.
B. BÀI TẬP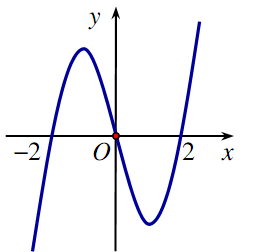
Câu 1. Cho hàm số f(x) xác định trên R và có đồ thị hàm số f'(x) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
A. Hàm số f(x) nghịch biến trên khoảng (-1;1) B. Hàm số f(x) đồng biến trên khoảng (1;2)
C. Hàm số f(x) đồng biến trên khoảng (-2;1) D. Hàm số f(x) nghịch biến trên khoảng (0;2)
Câu 2. Cho hàm số xác định trên và có đồ thị của hàm số như hình vẽ . Mệnh đề nào sau đây đúng?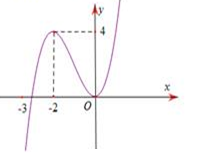
A. Hàm số y = f(x) đồng biến trên khoảng .
B. Hàm số y = f(x) nghịch biến trên khoảng (-2;0)
C. Hàm số y = f(x) đồng biến trên khoảng
D. Hàm số y = f(x) nghịch biến trên khoảng
Xem thêm