50 Bài tập Sự đồng biến nghịch biến của hàm số (có đáp án)- Toán 12

Bài tập Toán 9 Chương 1 Bài 1: Sự đồng biến nghịch biến của hàm số

A. Bài tập Sự đồng biến nghịch biến của hàm số

I. Bài tập trắc nghiệm

Bài 1: Cho hàm số y = sin2x – 2x. Hàm số này

A. Luôn đồng biến trên R    

B. Chỉ đồng biến trên khoảng (0; +∞)

C. Chỉ nghịch biến trên (-∞; -1)    

D. Luôn nghịch biến trên R

Lời giải:

Tập xác định D = R

Ta có : y’ = 2.cos2x – 2 = 2(cos2x – 1) ≤ 0; ∀ x

(vì -1 ≤ cos2x ≤ 1)

Vậy hàm số luôn nghịch biến trên R

Chọn đáp án D.

Bài 2: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?

Lời giải:

Bài 3: Tìm m để hàm số

luôn nghịch biến trên khoảng xác định.

A.-2 < m ≤ 2    

B. m < -2 hoặc m > 2

C. -2 < m < 2    

D. m ≠ ±2

Lời giải:

Tập xác định

Hàm số nghịch biến trên từng khoảng

khi và chỉ khi

Suy ra m² – 4 < 0 hay -2 < m < 2. Chọn đáp án C.

Bài 4: Cho hàm số y = -x³ + 3x² + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

A. m < 1   

B. m ≥ 1   

C. m ≤ -1   

D. m ≥ -1

Lời giải:

Ta có y’ = -3x² + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y’ ≤ 0 trên khoảng (o; +∞)

Cách 1: Dùng định lí dấu tam thức bậc hai.

Xét phương trình -3x² + 6x + 3m. Ta có Δ’ = 9(1 + m)

TH1: Δ’ ≤ 0 => m ≤ -1 khi đó, -3x² + 6x + 3m < 0 nên hàm số nghịch biến trên R .

TH2: Δ’ > 0 => m > -1; y’ = 0 có hai nghiệm phân biệt là x = 1 ±$\sqrt{\left(1+m\right)}$ .

Hàm số nghịch biến trên (0; +∞) <=> 1 + $\sqrt{\left(1+m\right)}$ ≤ 0, vô lí.

Từ TH1 và TH2, ta có m ≤ -1

Cách 2: Dùng phương pháp biến thiên hàm số.

Ta có y’ = ^–3x²+ 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x² – 6x, ∀x > 0

Từ đó suy ra 3m ≤ min(3x² – 6x) với x > 0

Mà 3x² -6x = 3(x² -2x + 1) – 3 = 3(x – 1)2 – 3 ≥ -3 ∀ x

Suy ra: min( 3x² – 6x) = – 3 khi x= 1

Do đó 3m ≤ -3 hay m ≤ -1.

Chọn đáp án C.

Bài 5: Cho đồ thị hàm số với x ∈ [- $\frac{\mathrm{\pi }}{2}$ ; $\frac{3\mathrm{\pi }}{2}$] như hình vẽ.

Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- $\frac{\mathrm{\pi }}{2}; \frac{3\mathrm{\pi }}{2}$]

Lời giải:

Trên khoảng (-$\frac{\pi }{2}; \frac{\pi }{2}$) đồ thị hàm số đi lên từ trái sang phải.

Trên khoảng ($\frac{\pi }{2}; \frac{3\pi }{2}$) đồ thị hàm số đi xuống từ trái sang phải.

Do đó hàm số đồng biến trên khoảng (-$\frac{\pi }{2}; \frac{\pi }{2}$)

Chọn đáp án A.

Bài 6: Cho đồ thị hàm số y = -x³ như hình vẽ. Hàm số y = -x³ nghịch biến trên khoảng:

A. (-1;0)    

B. (-∞;0)

C. (0;+∞)    

D. (-1;1)

Lời giải:

Trên khoảng (0; +∞) đồ thị hàm số đi xuống từ trái sang phải.

Do đó hàm số nghịch biến trên khoảng (0;+∞),

Chọn đáp án C.

Bài 7: Cho đồ thị hàm số y = –$\frac{2}{x}$ như hình vẽ. Hàm số y = –$\frac{2}{x}$ đồng biến trên

A. (-∞;0)   

B. (-∞;0) ∪ (0;+∞)

C. R    

D. (-∞;0) và (0;+∞)

Lời giải:

Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)

Chọn đáp án D.

Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:

– Không chú ý tập xác định nên chọn đáp án C.

– Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.

Bài 8: Cho hàm số f(x) có đạo hàm f'(x) = $\sqrt{x(x–1)(x+2)}$²

Kết luận nào sau đây là đúng?

A. Hàm số f(x) nghịch biến trên khoảng (-∞;1).

B. Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).

C. Hàm số f(x) đồng biến trên các khoảng và (1;+∞).

D. Hàm số f(x) đồng biến trên các khoảng (1;+∞).

Lời giải:

Điều kiện: x > 0

Bảng xét dấu :

Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).

Chọn đáp án D.

Bài 9: Khoảng nghịch biến của hàm số y = $x^{\frac{3}{3}}$ – 2x² + 3x + 5 là:

A. (1;3)    

B.(-∞; 1) ∪ (3; +∞)   

C. (-∞; 1) và (3; +∞)    

D. (1;+∞)

Lời giải:

Bảng xét dấu y’:

Vậy hàm số nghịch biến trên khoảng (1;3).

Chọn đáp án A.

Bài 10: Cho hàm số y = x⁴ – 2x² + 3 . Kết luận nào sau đây đúng?

A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)

B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)

C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)

D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)

Lời giải:

Bảng xét dấu y’:

Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) .

Chọn đáp án D.

II. Bài tập tự luận có lời giải

Bài 1: Cho hàm số y = x³ – x² + (m-1)x + m. Tìm điều kiện của tham số m để hàm số đồng biến trên R

Lời giải:

y’ = x² – 2x + (m -1).

Hàm số đồng biến trên R ⇔ y’ ≥ 0 ∀x ∈ R

⇒ Δ = (-1)2 – (m-1) = -m + 2 ≤ 0 ⇔ m > 2

Bài 2: Cho hàm số

Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).

Lời giải:

Ta có y’ = -x² – mx – 2 . Hàm số nghịch biến trên khoảng (-∞; – 1) nếu y’ = x² – mx – 2 ≤ 0 trên khoảng (-∞; -1)

Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m² – 8

TH1: -2$\sqrt{2}$ ≤ m ≤ 2$\sqrt{2}$ => Δ ≤ 0.

Lại có, hệ số a = -1 < 0 nên y’ ≤ 0 ∀ x

Hàm số nghịch biến trên R

TH2:  y’ = 0. có hai nghiệm phân biệt là 

Từ TH1 và TH2, ta có m ≤ 2$\sqrt{2}$

Cách 2. Dùng phương pháp biến thiên hàm số

Ta có

Từ đó suy ra

Do đó m ≤ 2$\sqrt{2}$

Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2$\sqrt{2}$

Bài 3: Tìm tất cả các giá trị của tham số m sao cho hàm số

Lời giải:

Bài 4: Cho hàm số y = x³ + 3x² + mx + 1 – 2m. Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.

Lời giải:

y’ = 3x² + 6x + m. Hàm số đồng biến nếu y’ ≥ 0. Ta có Δ’ = 9 – 3m

TH1: m ≥ 3 => Δ’ ≤ 0 .

Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài

TH2: m < 3 => Δ’ > 0 .

y’ có hai nghiệm phân biệt là

Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.

Từ TH1 và TH2, không tồn tại m thỏa mãn.

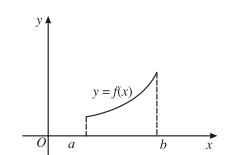
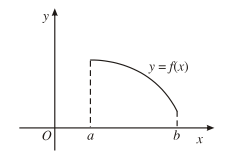
Bài 5: Cho đồ thị hàm số có dạng như hình vẽ.

Hàm số đồng biến trên?

Lời giải:

Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải

Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải

Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)

Bài 6: Hỏi hàm số

đồng biến trên các khoảng nào?

Lời giải:

Hàm số xác định ∀x ≠ -5

y’ xác định ∀x ≠ -5 . Bảng xét dấu y’:

Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)

Bài 7: Tìm khoảng đồng biến của hàm số y = 2x³ – 9x³ + 12x + 3

Lời giải:

Ta có

Bảng xét dấu đạo hàm:

Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)

Bài 8: Khoảng nghịch biến của hàm số y = x⁴ – 2x² – 1 là:

Lời giải:

Ta có

Bảng xét dấu đạo hàm

Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)

Bài 9: Cho hàm số

Khẳng định nào sau đây là khẳng định đúng?

Lời giải:

Hàm số

xác định ∀x ≠ 1

Ta có:

xác định ∀x ≠ 1

Bảng xét dấu đạo hàm

Hàm số nghịch biến trên các khoảng (-∞ 1) và (1; +∞)

Bài 10: Tìm khoảng đồng biến của hàm số f(x)= x + cos2x

Lời giải:

f'(x) = 1 – 2sinxcosx = sin²x + cos²x – 2.sinx.cosx = (sinx – cosx)² ≥ 0 ∀x ∈ R

Hàm số đồng biến trên khoảng (-∞; +∞)

III. Bài tập vận dụng

Lời giải:

Bài 1 Hàm số:

đồng biến trên khoảng nào?

Lời giải:

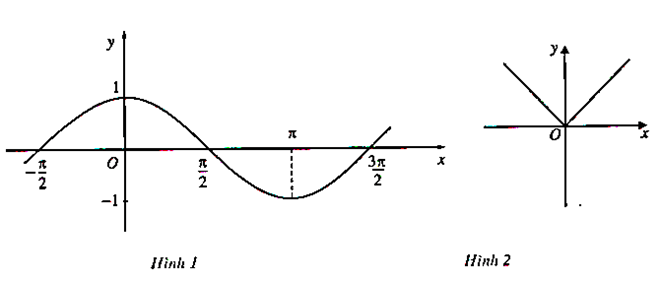
Bài 2 Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [$\frac{\left(–\pi \right)}{2}$; $\frac{3\pi }{2}$] và các hàm số y = |x| trên khoảng (-∞; +∞).

Bài 3 Xét các hàm số sau và đồ thị của chúng:

a) y = –$\frac{x^2}{2}$ (H.4a)       b) y = $\frac{1}{x}$ (H.4b)

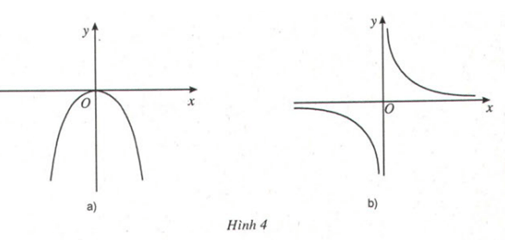
Xét dấu đạo hàm của mỗi hàm số và điền vào bảng tương ứng.

Bài 4 Khẳng định ngược lại với định lí trên có đúng không ? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên K thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không ?

Bài 5 Xét sự đồng biến, nghịch biến của hàm số:

a) y = 4 + 3x – x²

b) y = $\frac{1}{3}$.x³ + 3x² – 7x -2

c) y = x⁴ – 2x² + 3

d) y = -x³ + x² – 5

Bài 6 Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?

Bài 7 Cho hàm số y = -x³ + 3x² + 3mx – 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)

Bài 8 Cho đồ thị hàm số với x ∈ [- $\frac{\pi }{2}; \frac{3\pi }{2}$] như hình vẽ.

Bài 9 Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- $\frac{\pi }{2}$ ; $\frac{3\pi }{2}$]

Bài 10 Chứng minh rằng hàm số  đồng biến trên khoảng (0;1) và nghịch biến trên khoảng (1,2).

B. Lý thuyết Sự đồng biến nghịch biến của hàm số

I. Tính đơn điệu của hàm số

1. Nhắc lại định nghĩa

– Định nghĩa:

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:

Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) nhỏ hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$ f(x₁) < f(x₂).

Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x₁; x₂ thuộc K mà x₁ nhỏ hơn x₂ thì f(x₁) lớn hơn f(x₂), tức là

x₁ < x₂ $\Rightarrow$f(x₁) > f(x₂).

– Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.

– Nhận xét: Từ định nghĩa trên ta thấy:

a) f(x) đồng biến trên K$\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}>\text{}0;$ $\hspace{0.17em}\forall x_1;x_2\in K;(x_1\ne x_2)$

f(x) nghịch biến trên K$\iff \frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}<\text{\hspace{0.17em}}0;$$\hspace{0.17em}\forall x_1;x_2\in K;(x_1\ne x_2)$

b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

2. Tính đơn điệu và dấu của đạo hàm

– Định lí:

Cho hàm số y = f(x) có đạo hàm trên K.

a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.

b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

– Chú ý:

Nếu f’(x) = 0 với $\forall x\in \text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}K$ thì f(x) không đổi trên K.

Ví dụ 1. Tìm các khoảng đơn điệu của hàm số

a) y = x² + 2x – 10;

b) $y=\frac{x+5}{2x-3}$

Lời giải:
a) Hàm số đã cho xác định với mọi x$\in ℝ$

Ta có  đạo hàm y’ = 2x + 2

Và y’ = 0 khi x = – 1.

Lập bảng biến thiên:

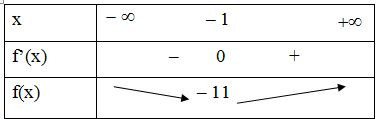
Vậy hàm số đã cho đồng biến trên khoảng $\left(-1;+\text{\hspace{0.17em}}\infty \right)$ và nghịch biến trên khoảng $\left(-\infty ;-1\right)$.

b) $y=\frac{x+5}{2x-3}$

Hàm số đã cho xác định với $\forall x\ne \frac{3}{2}$

Ta có: $y‘=\frac{-13}{{(2x-3)}^2}<0\forall x\ne \frac{3}{2}$

Do đó, hàm số đã cho nghịch biến trên khoảng $\left(-\infty ;\frac{3}{2}\right)$ và $\left(\frac{3}{2};+\text{\hspace{0.17em}}\infty \right)$

– Chú ý:

Ta có định lí mở rộng sau đây:

Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu $f^{‘}\left(x\right)\ge 0\left(f^{‘}\left(x\right)\le 0\right);\forall x\in K$

Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.

Ví dụ 2.  Tìm các khoảng đơn điệu của hàm số y = x³ – 6x² + 12x – 10.

Lời giải:

Hàm số đã cho xác định với mọi x$\in R$

Ta có: y’ = 3x² – 12x + 12 = 3(x – 2)²

Do đó; y’ = 0 khi x = 2 và y’ > 0 với $\forall x\ne 2$

Theo định lí mở rộng, hàm số đã cho luôn luôn đồng biến trên R.

II. Quy tắc xét tính đơn điệu của hàm số.

1. Quy tắc

– Bước 1. Tìm tập xác định.

– Bước 2. Tính đạo hàm  f’(x). Tìm các điểm x_i  ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

– Bước 3. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

– Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

2. Áp dụng

Ví dụ 3. Xét sự đồng biến, nghịch biến của hàm số y = x⁴ – 2x² – 3.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = 4x³ – 4x

y’ = 0$\iff \left[\begin{array}{c}x=0\\ x=\pm 1\end{array}\right.$

Bảng biến thiên:

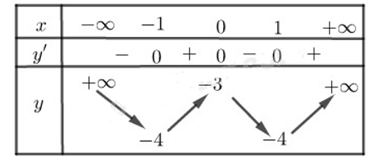
Vậy hàm số đã cho đồng biến trên (– 1; 0) và $(1;+\infty )$

Hàm số nghịch biến trên $\left(-\infty ;-1\right)$ và (0; 1).

Ví dụ 4.  Cho hàm số $y=-x^3+6x^2-\text{\hspace{0.17em}\hspace{0.17em}}9x+3$. Xét tính đồng biến, nghịch biến của hàm số trên.

Lời giải:

Hàm số đã cho xác định với mọi x.

Ta có: y’ = – 3x² + 12x – 9

Và y’ = 0$\iff \left[\begin{array}{c}x=1\\ x=3\end{array}\right.$

Bảng biến thiên:

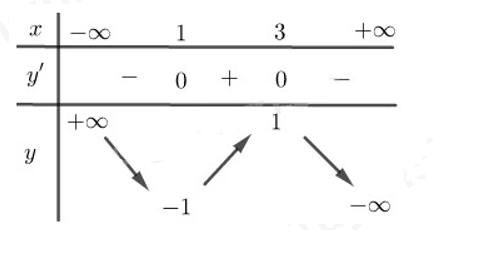
Vậy hàm số đã cho đồng biến trên (1; 3); nghịch biến trên $(-\infty ;1)$ và $(3;+\infty )$.