Câu hỏi:
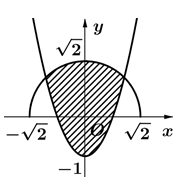
Cho (H) là hình phẳng giới hạn bởi parabol \(y = 2{x^2} – 1\) và nửa đường tròn có phương trình \(y = \sqrt {2 – {x^2}} \) (với \( – \sqrt 2 \le x \le \sqrt 2 \)) (phần gạch chéo trong hình vẽ). Diện tích của (H) bằng
A.
\(\frac{{3\pi + 2}}{6}.\)
B.\(\frac{{3\pi – 2}}{6}.\)
C.\(\frac{{3\pi + 10}}{6}.\)
Đáp án chính xác
D.\(\frac{{3\pi + 10}}{3}.\)
Trả lời:
Chọn đáp án C
Phương trình hoành độ giao điểm của hai đồ thị là: \(2{x^2} – 1 = \sqrt {2 – {x^2}} \)
\( \Leftrightarrow \left\{ \begin{array}{l}2{x^2} – 1 \ge 0\\4{x^4} – 4{x^2} + 1 = 2 – {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x^2} – 1 \ge 0\\4{x^4} – 3{x^2} – 1 = 0\end{array} \right. \Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\).
Diện tích hình \(\left( H \right)\) bằng: \(S = 2\int\limits_0^1 {\left( {\sqrt {2 – {x^2}} – 2{x^2} + 1} \right)dx} = 2\int\limits_0^1 {\sqrt {2 – {x^2}} dx} + 2\int\limits_0^1 {\left( { – 2{x^2} + 1} \right)dx} \)
\( = 2{I_1} + \left. {2\left( {\frac{{ – 2{x^3}}}{3} + x} \right)} \right|_0^1 = 2{I_1} + \frac{2}{3}\).
Tính \({I_1} = \int\limits_0^1 {\sqrt {2 – {x^2}} dx} \) đặt \(x = \sqrt 2 \sin t \Rightarrow dx = \sqrt 2 \cos tdt\) với \(t \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]\)
Đổi cận\(\left| \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = \frac{\pi }{4}\end{array} \right.\)\( \Rightarrow {I_1} = \int\limits_0^{\frac{\pi }{4}} {\sqrt {2 – 2{{\sin }^2}t} .\sqrt 2 \cos tdt} = \int\limits_0^{\frac{\pi }{4}} {2{{\cos }^2}tdt} = \int\limits_0^{\frac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt} \)
\( = \left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\frac{\pi }{4}} = \frac{\pi }{4} + \frac{1}{2} \Rightarrow S = 2{I_1} + \frac{2}{3} = \frac{\pi }{2} + 1 + \frac{2}{3} = \frac{{3\pi + 10}}{6}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \cos 3x\) là
Câu hỏi:
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \cos 3x\) là
A.\( – \frac{1}{3}\sin 3x + C.\)
B.\(\frac{1}{3}\sin 3x + C.\)
Đáp án chính xác
C.\( – 3\sin 3x + C.\)
D.\(3\sin 3x + C.\)
Trả lời:
Lời giải:
Chọn đáp án B
Ta có \(\int {\cos 3xdx} = \frac{{\sin 3x}}{3} + C\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Câu hỏi:
Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\(\vec n = \left( {0; – 4;3} \right).\)
B.\(\vec n = \left( {1{\mkern 1mu} ;{\mkern 1mu} 4{\mkern 1mu} ;{\mkern 1mu} 3} \right).\)
C.\(\vec n = \left( { – 1;4; – 3} \right).\)
Đáp án chính xác
D.\(\vec n = \left( { – 4;3; – 2} \right).\)
Trả lời:
Chọn đáp án C
Mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0\) có một VTPT là \(\overrightarrow n = \left( { – 1;4; – 3} \right)\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
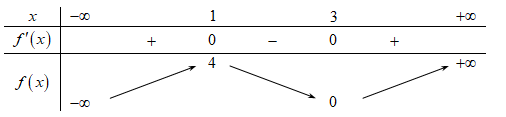Hàm số đã cho nghịch biến trên khoảng nào dưới đây?A.\(\left( { – \infty ;1} \right).\)
B.\(\left( {3; + \infty } \right).\)
C.\(\left( {0;4} \right).\)
D.\(\left( {1;3} \right).\)
Đáp án chính xác
Trả lời:
Lời giải:Chọn đáp án DHàm số \(f\left( x \right)\) nghịch biến trên \(\left( {1;3} \right)\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:Giá trị cực đại của hàm số đã cho là
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
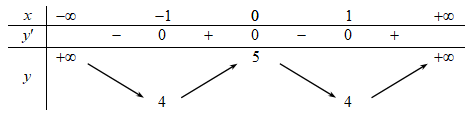Giá trị cực đại của hàm số đã cho làA.4.
B.0.
C.1.
D.5.
Đáp án chính xác
Trả lời:
Lời giải:Chọn đáp án DGiá trị cực đại của hàm số \(f\left( x \right)\) là 5
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính đạo hàm của hàm số \(y = {\log _2}\sqrt {2x + 3} .\)
Câu hỏi:
Tính đạo hàm của hàm số \(y = {\log _2}\sqrt {2x + 3} .\)
A.\(y’ = \frac{2}{{2x + 3}}.\)
B.\(y’ = \frac{1}{{2x + 3}}.\)
C.\(y’ = \frac{2}{{\left( {2x + 3} \right)\ln 2}}.\)
D.\(y’ = \frac{1}{{\left( {2x + 3} \right)\ln 2}}.\)
Đáp án chính xác
Trả lời:
Chọn đáp án D
Ta có \(y = \frac{1}{2}{\log _2}\left( {2x + 3} \right) \Rightarrow y’ = \frac{1}{2}.\frac{{{{\left( {2x + 3} \right)}^\prime }}}{{\left( {2x + 3} \right)\ln 2}} = \frac{1}{{\left( {2x + 3} \right)\ln 2}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====