Câu hỏi:
Cho hình lăng trụ \(ABC.A’B’C’\). Gọi M, N, P lần lượt là các điểm thuộc các cạnh \(AA’\), \(BB’\), \(CC’\) sao cho \(AM = 2MA’\), \(NB’ = 2NB\), \(PC = PC’\). Gọi \({V_1}\), \({V_2}\) lần lượt là thể tích của hai khối đa diện \(ABCMNP\) và \(A’B’C’MNP\). Tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
A.\(\frac{{{V_1}}}{{{V_2}}} = 2\)
B.\(\frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\)
C.\(\frac{{{V_1}}}{{{V_2}}} = 1\)
Đáp án chính xác
D.\(\frac{{{V_1}}}{{{V_2}}} = \frac{2}{3}\)
Trả lời:
Chọn đáp án C
Gọi Vlà thể tích khối lăng trụ \(ABC.A’B’C’\)
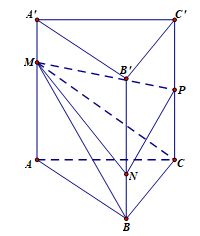
Ta có \({V_1} = {V_{M.ABC}} + {V_{M.BCPN}}\).
\({V_{M.ABC}} = \frac{1}{3}d\left( {M;\left( {ABC} \right)} \right).{S_{ABC}} = \frac{1}{3}.\frac{2}{3}d\left( {A’;\left( {ABC} \right)} \right).{S_{ABC}} = \frac{2}{9}V\).
\(\frac{{{V_{M.BCPN}}}}{{{V_{M.BCC’B’}}}} = \frac{{{S_{BCPN}}}}{{{S_{BCC’B’}}}} = \frac{{\frac{1}{2}d\left( {C;BB’} \right).\left( {BN + CP} \right)}}{{\frac{1}{2}d\left( {C;BB’} \right).\left( {BB’ + CC’} \right)}} = \frac{{BN + CP}}{{BB’ + CC’}} = \frac{{\frac{1}{3}BB’ + \frac{1}{2}CC’}}{{BB’ + CC’}}\)
\( \Rightarrow {V_{M.BCPN}} \Rightarrow \frac{5}{{12}}{V_{M.BCC’B’}} = \frac{5}{{12}}{V_{A.BCC’B’}} = \frac{5}{{12}}.2{V_{ABC’B’}} = \frac{5}{{12}}.2.\frac{1}{3}V = \frac{5}{{18}}V\)
\( \Rightarrow {V_1} = {V_{M.ABC}} + {V_{M.BCPN}} = \frac{2}{9}V + \frac{5}{{18}}V = \frac{1}{2}V \Rightarrow {V_2} = V – \frac{1}{2}V = \frac{1}{2}V \Rightarrow \frac{{{V_1}}}{{{V_2}}} = 1\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \cos 3x\) là
Câu hỏi:
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \cos 3x\) là
A.\( – \frac{1}{3}\sin 3x + C.\)
B.\(\frac{1}{3}\sin 3x + C.\)
Đáp án chính xác
C.\( – 3\sin 3x + C.\)
D.\(3\sin 3x + C.\)
Trả lời:
Lời giải:
Chọn đáp án B
Ta có \(\int {\cos 3xdx} = \frac{{\sin 3x}}{3} + C\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
Câu hỏi:
Trong không gian Oxyz,cho mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của (P)?
A.\(\vec n = \left( {0; – 4;3} \right).\)
B.\(\vec n = \left( {1{\mkern 1mu} ;{\mkern 1mu} 4{\mkern 1mu} ;{\mkern 1mu} 3} \right).\)
C.\(\vec n = \left( { – 1;4; – 3} \right).\)
Đáp án chính xác
D.\(\vec n = \left( { – 4;3; – 2} \right).\)
Trả lời:
Chọn đáp án C
Mặt phẳng \(\left( P \right):x – 4y + 3z – 2 = 0\) có một VTPT là \(\overrightarrow n = \left( { – 1;4; – 3} \right)\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
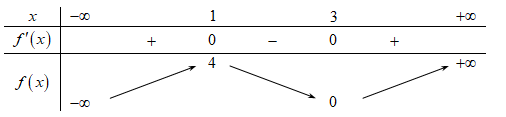Hàm số đã cho nghịch biến trên khoảng nào dưới đây?A.\(\left( { – \infty ;1} \right).\)
B.\(\left( {3; + \infty } \right).\)
C.\(\left( {0;4} \right).\)
D.\(\left( {1;3} \right).\)
Đáp án chính xác
Trả lời:
Lời giải:Chọn đáp án DHàm số \(f\left( x \right)\) nghịch biến trên \(\left( {1;3} \right)\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số f(x) có bảng biến thiên như sau:Giá trị cực đại của hàm số đã cho là
Câu hỏi:
Cho hàm số f(x) có bảng biến thiên như sau:
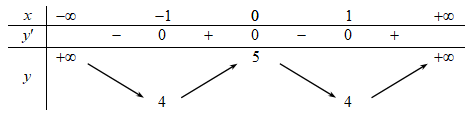Giá trị cực đại của hàm số đã cho làA.4.
B.0.
C.1.
D.5.
Đáp án chính xác
Trả lời:
Lời giải:Chọn đáp án DGiá trị cực đại của hàm số \(f\left( x \right)\) là 5
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính đạo hàm của hàm số \(y = {\log _2}\sqrt {2x + 3} .\)
Câu hỏi:
Tính đạo hàm của hàm số \(y = {\log _2}\sqrt {2x + 3} .\)
A.\(y’ = \frac{2}{{2x + 3}}.\)
B.\(y’ = \frac{1}{{2x + 3}}.\)
C.\(y’ = \frac{2}{{\left( {2x + 3} \right)\ln 2}}.\)
D.\(y’ = \frac{1}{{\left( {2x + 3} \right)\ln 2}}.\)
Đáp án chính xác
Trả lời:
Chọn đáp án D
Ta có \(y = \frac{1}{2}{\log _2}\left( {2x + 3} \right) \Rightarrow y’ = \frac{1}{2}.\frac{{{{\left( {2x + 3} \right)}^\prime }}}{{\left( {2x + 3} \right)\ln 2}} = \frac{1}{{\left( {2x + 3} \right)\ln 2}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====