Câu hỏi:
Cho phương trình \(\log _3^2\left( {3x} \right) – \left( {m + 2} \right){\log _3}x + m – 2 = 0\) (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn \(\left[ {\frac{1}{3};3} \right]\) là
A. \(\left( {0;2} \right).\)
B. \(\left[ {0;2} \right].\)
C. \(\left[ {0;2} \right).\)
Đáp án chính xác
D. \(\left( {2; + \infty } \right).\)
Trả lời:
Đáp án C
Điều kiện: \(x > 0\)
Ta có: \({\log _3}^2\left( {3x} \right) – \left( {m + 2} \right){\log _3}x + m – 2 = 0 \Leftrightarrow {\log _3}^2x – m{\log _3}x + m – 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{{\log }_3}x = 1}\\{{{\log }_3}x = m – 1}\end{array}} \right.\)
Phương trình: \({\log _3}x = 1 \Leftrightarrow x = 3 \in \left[ {\frac{1}{3};3} \right]\)
Để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn \(\left[ {\frac{1}{3};3} \right]\) thì phương trình:
\({\log _3}x = m – 1\) có 1 nghiệm thuộc \(\left[ {\frac{1}{3};3} \right).\)
\( \Rightarrow {\log _3}\frac{1}{3} \le {\log _3}x = m – 1 < {\log _3}3 \Leftrightarrow – 1 \le m – 1 < 1 \Leftrightarrow 0 \le m < 2 \Rightarrow m \in \left[ {0;2} \right)\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz cho \(E\left( { – 1;0;2} \right)\) và \(F\left( {2;1; – 5} \right).\) Phương trình đường thẳng EF là
Câu hỏi:
Trong không gian Oxyz cho \(E\left( { – 1;0;2} \right)\) và \(F\left( {2;1; – 5} \right).\) Phương trình đường thẳng EF là
A. \(\frac{{x – 1}}{3} = \frac{y}{1} = \frac{{z + 2}}{{ – 7}}.\)
B. \(\frac{{x + 1}}{3} = \frac{y}{1} = \frac{{z – 2}}{{ – 7}}.\)
Đáp án chính xác
C. \(\frac{{x – 1}}{1} = \frac{y}{1} = \frac{{z + 2}}{{ – 3}}.\)
D. \(\frac{{x + 1}}{1} = \frac{y}{1} = \frac{{z – 2}}{3}.\)
Trả lời:
Đáp án B
Đường thẳng EF có véc tơ chỉ phương \(\overrightarrow {EF} = \left( {3;1; – 7} \right) \Rightarrow \left( {EF} \right):\frac{{x + 1}}{3} = \frac{y}{1} = \frac{{z – 2}}{{ – 7}}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ như sau
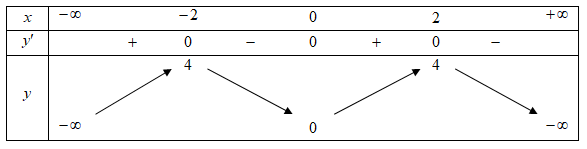
Hàm số đã cho nghịch biến trên khoảng nào dưới đâyA. \(\left( { – 4;0} \right).\)
B. \(\left( {2; + \infty } \right).\)
Đáp án chính xác
C. \(\left( { – 2;2} \right).\)
D. \(\left( {0;4} \right).\)
Trả lời:
Đáp án B
Hàm số đã cho nghịch biến trên từng khoảng \(\left( { – 2;0} \right),\left( {2; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập tất cả các số thực x thỏa mãn \({\left( {\frac{2}{3}} \right)^{4x}} \le {\left( {\frac{3}{2}} \right)^{2 – x}}\) là:
Câu hỏi:
Tập tất cả các số thực x thỏa mãn \({\left( {\frac{2}{3}} \right)^{4x}} \le {\left( {\frac{3}{2}} \right)^{2 – x}}\) là:
A. \(\left[ { – \frac{2}{3}; + \infty } \right).\)
Đáp án chính xác
B. \(\left[ {\frac{2}{5}; + \infty } \right).\)
C. \(\left( { – \infty ;\frac{2}{5}} \right].\)
D. \(\left( { – \infty ;\frac{2}{3}} \right].\)
Trả lời:
Đáp án A
Biến đổi về \({\left( {\frac{3}{2}} \right)^{ – 4x}} \le {\left( {\frac{3}{2}} \right)^{2 – x}} \Rightarrow – 4x \le 2 – x \Rightarrow x \ge – \frac{2}{3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số nhân \(\left( {{u_n}} \right)\), với \({u_1} = – 9,{u_4} = \frac{1}{3}.\) Công bộ của cấp số nhân đã cho bằng
Câu hỏi:
Cho cấp số nhân \(\left( {{u_n}} \right)\), với \({u_1} = – 9,{u_4} = \frac{1}{3}.\) Công bộ của cấp số nhân đã cho bằng
A. \(\frac{1}{3}.\)
B. \( – 3.\)
C. 3.
D. \( – \frac{1}{3}.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \({u_4} = {u_1}.{q^3} \Rightarrow \frac{1}{3} = – 9.{q^3} \Rightarrow {q^3} = – \frac{1}{{27}} \Rightarrow q = – \frac{1}{3}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây
Câu hỏi:
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây
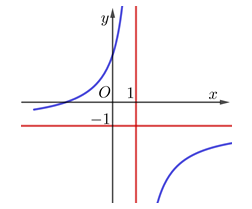
A. \(y = \frac{{ – x + 2}}{{x – 1}}.\)
B. \(y = \frac{{x – 1}}{{x + 1}}.\)
C. \(y = \frac{{ – x – 2}}{{x – 1}}.\)
Đáp án chính xác
D. \(y = \frac{{x – 2}}{{x – 1}}.\)
Trả lời:
Đáp án C
ĐTHS có tiệm cận đứng \(x = 1 \Rightarrow \) Loại B
ĐTHS có tiệm cận ngang \(y = – 1 \Rightarrow \) Loại D
Hàm số đồng biến trên từng khoảng xác định \( \Rightarrow \) Loại A vì có \(y’ = \frac{{ – 1}}{{{{\left( {x – 1} \right)}^2}}}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====