Câu hỏi:
Cho hình lăng trụ đứng \(ABC.A’B’C’\) có đáy ABC là tam giác đều. Cạnh \(AA’ = a\sqrt 6 \) và khoảng cách từ điểm A đến mặt phẳng \(\left( {A’BC} \right)\) là \(a\sqrt 2 \). Tính thể tích V của khối lăng trụ \(ABC.A’B’C’\).
A. \(V = {a^3}\sqrt 2 \).
B. \(V = 2{a^3}\sqrt 2 \).
C. \(V = 3{a^3}\sqrt 2 \).
Đáp án chính xác
D. \(V = 4{a^3}\sqrt 2 \).
Trả lời:
Đáp án C
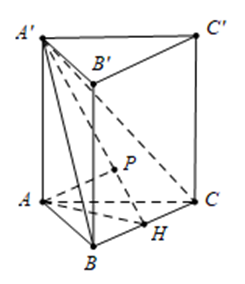
Kẻ \(AH \bot BC,AP \bot A’H \Rightarrow d\left( {A’;\left( {A’BC} \right)} \right) = AP = a\sqrt 2 \).
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{P^2}}} – \frac{1}{{A'{A^2}}} \Rightarrow AH = a\sqrt 3 \).
\(\Delta ABC\) đều \( \Rightarrow AH = \frac{{AB\sqrt 3 }}{2} \Rightarrow AB = 2a\)
\( \Rightarrow V = AA’.{S_{ABC}} = AA’ – \frac{{A{B^2}\sqrt 3 }}{4} = 3{a^3}\sqrt 2 \).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{2} = \frac{{z – 3}}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của \(d\)?
Câu hỏi:
Trong không gian Oxyz, cho đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{2} = \frac{{z – 3}}{3}\). Vectơ nào dưới đây là một vectơ chỉ phương của \(d\)?
A. \(\overrightarrow u = \left( { – 1;2; – 3} \right)\).
B. \(\overrightarrow u = \left( {1;2;3} \right)\).
Đáp án chính xác
C. \(\overrightarrow u = \left( {1;2; – 3} \right)\).
D. \(\overrightarrow u = \left( { – 1;2;3} \right)\).
Trả lời:
Đáp án B
Đường thẳng \(d:\frac{{x – 1}}{1} = \frac{{y – 2}}{2} = \frac{{z – 3}}{3}\) có một VTCP là \(\overrightarrow u = \left( {1;2;3} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Với a là số thực dương tùy ý, \(\ln \left( {8a} \right) – \ln \left( {3a} \right)\) bằng
Câu hỏi:
Với a là số thực dương tùy ý, \(\ln \left( {8a} \right) – \ln \left( {3a} \right)\) bằng
A. \(\ln \frac{8}{3}\).
Đáp án chính xác
B. \(\ln \frac{3}{8}\).
C. \(\frac{{\ln 8}}{{\ln 3}}\).
D. \(\frac{{\ln \left( {8a} \right)}}{{\ln \left( {3a} \right)}}\).
Trả lời:
Đáp án A
Ta có \(\ln \left( {8a} \right) – \ln \left( {3a} \right) = \ln \frac{{8a}}{{3a}} = \ln \frac{8}{3}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
\(x\)
\( – \infty \)
-2
0
\( + \infty \)
\(f'\left( x \right)\)
–
0
+
0
–
\(f\left( x \right)\)
\( + \infty \)
4
0
\( – \infty \)
Hàm số đã cho đạt cực tiểu tại
Câu hỏi:
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
\(x\)
\( – \infty \)
-2
0
\( + \infty \)
\(f’\left( x \right)\)
–
0
+
0
–
\(f\left( x \right)\)
\( + \infty \)
4
0
\( – \infty \)
Hàm số đã cho đạt cực tiểu tại
A. x = -2.
Đáp án chính xác
B. x = 0.
C. x = 1.
D. x = 4.
Trả lời:
Đáp án A
Hàm số \(f\left( x \right)\) đạt cực tiểu tại \(x = – 2\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {1;3;2} \right),{\rm{ }}\overrightarrow b = \left( {1;2;0} \right)\) và \(\overrightarrow c = \left( {0;1;2} \right)\). Tìm tọa độ vectơ \(\overrightarrow w = \overrightarrow a – \overrightarrow b + \overrightarrow c \).
Câu hỏi:
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {1;3;2} \right),{\rm{ }}\overrightarrow b = \left( {1;2;0} \right)\) và \(\overrightarrow c = \left( {0;1;2} \right)\). Tìm tọa độ vectơ \(\overrightarrow w = \overrightarrow a – \overrightarrow b + \overrightarrow c \).
A. \(\overrightarrow w = \left( {2;6;4} \right)\).
B. \(\overrightarrow w = \left( {0;2;4} \right)\).
Đáp án chính xác
C. \(\overrightarrow w = \left( {0;4;6} \right)\).
D. \(\overrightarrow w = \left( {0;2;6} \right)\).
Trả lời:
Đáp án B
Ta có \(\overrightarrow w = \overrightarrow a – \overrightarrow b + \overrightarrow c = \left( {1 – 1 + 0;3 – 2 + 1;2 – 0 + 2} \right) = \left( {0;2;4} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^1 {f\left( x \right)dx} = 5\). Tính phân \(\int\limits_0^1 {\left[ {2 + f\left( x \right)} \right]dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 5\). Tính phân \(\int\limits_0^1 {\left[ {2 + f\left( x \right)} \right]dx} \) bằng
A. 4.
B. 3.
C. 7.
D. 6.
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(I = \int\limits_0^1 {\left[ {2x + f\left( x \right)} \right]dx} = \int\limits_0^1 {2xdx} + \int\limits_0^1 {f\left( x \right)dx} = \left. {{x^2}} \right|_0^1 + 5 = 6\).====== **** mời các bạn xem câu tiếp bên dưới **** =====