Bài tập chuyên đề hình học không gian lớp 12 – có đáp án

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập chuyên đề hình học không gian lớp 12 – có đáp án

Bài tập thể tích khóa hình học không gian lớp 12

Các bài tập nhận biết

Bài 1: Cho tứ diện OABC. OA, OB, OC đôi một vuông góc, OA = a, OB = 2a, OC = 3a. Tính V_OABC.

A. \[\frac{{{a^3}}}{2}\]

B. a³

C. 2a³

D. 3a³

Lời giải

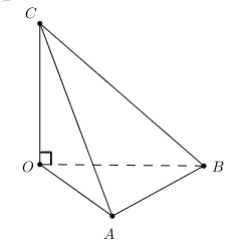
Chọn B.

Bài 2: Cho tất cả các cạnh hình lập phương tăng lên 2 lần thì thể tích hình lập phương tăng:

A. 4 lần

B. 6 lần

C. 8 lần

D. 16 lần

Lời giải: Cạnh tăng 2 lần thì V tăng 2³ = 8 lần. Chọn C

Bài 3: Chóp S.ABC, SA ABC ABC ⊥ D ( ), đều, AB = a, \[\widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = {60^0}\]. Tính V_S.ABC

A. \[\frac{{\sqrt 3 {a^3}}}{8}\]

B. \[\frac{{{a^3}}}{8}\]

C. \[\frac{{\sqrt 3 {a^3}}}{2}\]

D. \[\frac{{{a^3}}}{3}\]

Lời giải:

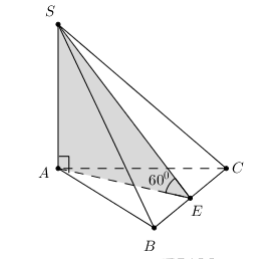
+ Vẽ \[AE \bot BC \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {SEA} = {60^0}\]

+  Xét tam giác vuông SAE: \[\tan {60^0} = \frac{{SA}}{{\frac{{a\sqrt 3 }}{2}}} \Rightarrow SA = \frac{{3a}}{2}\]

+ V_S.ABC = \[\frac{1}{3}.SA.\frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{\sqrt 3 {a^3}}}{8}\]

Chọn A

Bài 4: Chóp S.ABCD, SA ⊥ (ABCD) SA = 3a , ABCD là hình vuông cạnh a, tâm O. Tính V_SOBC.

A. a³

B. \[\frac{{{a^3}}}{2}\]

C. \[\frac{{{a^3}}}{3}\]

D. \[\frac{{{a^3}}}{4}\]

Lời giải:

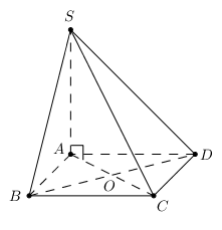
S_ABOC = \[\frac{1}{4}{S_{ABCD}} = \frac{{{a^2}}}{4}\]

V_SOBC =$\frac{1}{3}SA.S_{△BOC}=\frac{1}{3}.3a.\frac{a^2}{4}=\frac{a^3}{4}$

Chọn D.

Bài 5: Chóp đều S.ABCD, AB = a, \[\widehat {\left( {SA;\left( {ABCD} \right)} \right)} = {60^0}\]. Tính V_S.ABCD.

A. \[\frac{{\sqrt 6 {a^3}}}{6}\]

B. \[\frac{{{a^3}}}{6}\]

C. \[\frac{{{a^3}}}{2}\]

D. \[\frac{{{a^3}}}{3}\]

Lời giải:

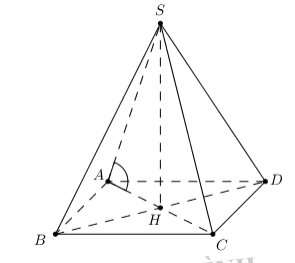
\[\widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {SAH} = {60^0}\]

Xét tam giác vuông SAH:

\[\tan {60^0} = \frac{{SH}}{{AH}} \Rightarrow SH = \sqrt 3 .\frac{{a\sqrt 2 }}{2} = \frac{{a\sqrt 6 }}{2}\]

V_S.ABCD = \[\frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 6 }}{2}.{a^2} = \frac{{\sqrt 6 {a^3}}}{6}\].

Chọn A.

Các bài tập vận dụng

Bài 6: Chóp S.ABCD, ABCD là hình thoi, AB = a, đáy, AC Ç BD = O,

\[\widehat {\left( {SO;\left( {SAB} \right)} \right)} = {30^0}\]. Tính V_S.ABCD.

A. \[\frac{{\sqrt 3 {a^3}}}{{12}}\]

B. \[\frac{{{a^3}\sqrt 5 }}{{12}}\]

C. \[\frac{{\sqrt 6 {a^3}}}{{12}}\]

D. \[\frac{{{a^3}\sqrt 7 }}{{12}}\]

Lời giải:

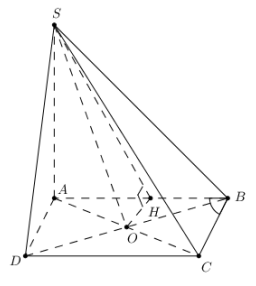
đều

\[ \Rightarrow OA = \frac{a}{2};OB = \frac{{a\sqrt 3 }}{2}\]

Vẽ OH ⊥ AB Þ OH ⊥ (SAB)

\[ \Rightarrow \widehat {\left( {SO;\left( {SAB} \right)} \right)} = \widehat {\left( {SO;SH} \right)} = \widehat {OSH} = {30^0}\]

Xét tam giác vuông AOB:

\[\frac{1}{{O{H^2}}} = \frac{4}{{{a^2}}} + \frac{4}{{3{a^2}}} \Rightarrow OH = \frac{{a\sqrt 3 }}{4}\]

Xét tam giác vuông SHO:

\[\sin {30^0} = \frac{{OH}}{{SO}} \Rightarrow SO = \frac{{\frac{{a\sqrt 3 }}{4}}}{{\frac{1}{2}}} = \frac{{a\sqrt 3 }}{2}\]

Xét tam giác vuông SAO:

 \[SA = \sqrt {S{O^2} – A{O^2}}  = \sqrt {\frac{{3{a^2}}}{4} – \frac{{{a^2}}}{4}}  = \frac{{a\sqrt 2 }}{2}\]

V_S.ABCD = \[\frac{1}{3}.\frac{{a\sqrt 2 }}{2}.2.\frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 6 }}{{12}}\]

Chọn C.

Bài 7: Chóp đều S.ABCD, H là tâm đáy, AB = a, d (AD;SB) = \[\frac{{2a}}{{\sqrt 5 }}\]. Tính V_S.ABCD.

A. \[\frac{{{a^3}}}{2}\]

B. \[\frac{{{a^3}}}{3}\]

C. \[\frac{{{a^3}}}{4}\]

D. \[\frac{{{a^3}}}{5}\]

Lời giải:

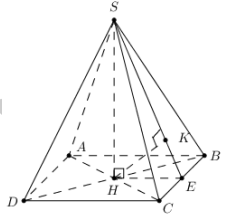
Ta có (SBC) chứa SB và song song với AD

\[\begin{array}{l} \Rightarrow d(AD;SB) = d(D;(SBC)) = 2d(H;(SBC))\\ = 2HK = \frac{{2a}}{{\sqrt 5 }} \Rightarrow HK = \frac{a}{{\sqrt 5 }}.\end{array}\]

Xét tam giác vuông SHE có : \[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{E^2}}}\]

\[ \Rightarrow \frac{1}{{S{H^2}}} = \frac{1}{{H{K^2}}} – \frac{1}{{H{E^2}}} = \frac{5}{{{a^2}}} – \frac{4}{{{a^2}}} = \frac{1}{{{a^2}}} \Rightarrow SH = a\]

\[ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}.SH.{S_d} = \frac{{{a^3}}}{3}.\]

Chọn B.

Bài 8: Hình chóp S.ABC, DABC đều, AB = a, M là trung điểm của AB, H là trung điểm của MC. \[SH \bot (ABC),\widehat {\left( {SB;\left( {ACB} \right)} \right)} = {60^0}\]. Tính V_S.ABC

A. \[\frac{{\sqrt 7 {a^3}}}{{13}}\]

B. \[\frac{{{a^3}\sqrt 7 }}{{14}}\]

C. \[\frac{{\sqrt 7 {a^3}}}{{15}}\]

D. \[\frac{{{a^3}\sqrt 7 }}{{16}}\]

Lời giải

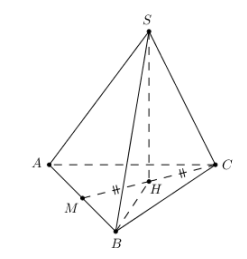
\[\widehat {\left( {SB;\left( {ACB} \right)} \right)} = \widehat {(SB;BH)} = \widehat {SHB} = {60^0}\]

Xét $△ABC:CM=\frac{a\sqrt{3}}{2}\Rightarrow HM=\frac{a\sqrt{3}}{4}$

Xét tam giác vuông BMH:

\[BH = \sqrt {H{M^2} + B{M^2}}  = \sqrt {\frac{{3{a^2}}}{{16}} + \frac{{{a^2}}}{4}}  = \frac{{a\sqrt 7 }}{4}\]

Xét tam giác vuông SHB:

\[\begin{array}{l}SH = BH.\tan {60^0} = \frac{{a\sqrt 7 }}{4}.\sqrt 3  = \frac{{a\sqrt {21} }}{4}\\V = \frac{1}{3}SH.{S_{\Delta ABC}} = \frac{1}{3}.\frac{{a\sqrt {21} }}{4}.\frac{1}{2}.a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 7 }}{{16}}\end{array}\]

Chọn D.

Bài 9: : Chóp SABC có SA = SB = SC = a. \[\widehat {ASB} = \widehat {ASC} = {60^0},\widehat {BSC} = {90^0}\]. Tính thể tích hình chóp SABC.

A. \[\frac{{\sqrt 2 {a^3}}}{{12}}\]

B. \[\frac{{{a^3}\sqrt 2 }}{7}\]

C. \[\frac{{\sqrt 2 {a^3}}}{6}\]

D. \[\frac{{{a^3}\sqrt 2 }}{5}\]

Lời giải

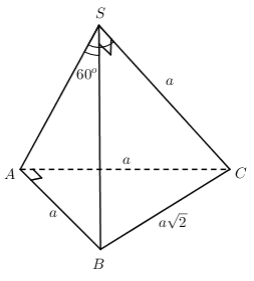
\[\begin{array}{l}\widehat {ASB} = \widehat {ASC} = {60^0} \Rightarrow AB = AC = a\\\widehat {BSC} = {90^0} \Rightarrow BC = a\sqrt 2 \end{array}\]

Nhận xét: Tam giác ABC có

AB² + AC² = 2a² = BC² Þ D ABC vuông ở A

R_d = \[\frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}\]

\[\begin{array}{l}h = \sqrt {S{A^2} – {R_d}^2}  = \sqrt {{a^2} – \frac{{2{a^2}}}{4}}  = \frac{{a\sqrt 2 }}{2}\\{S_d} = \frac{1}{2}AB.AC = \frac{{{a^2}}}{2}\\{V_{SABC}} = \frac{1}{3}.h.{S_d} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.\frac{{{a^2}}}{2} = \frac{{\sqrt 2 {a^3}}}{{12}}\end{array}\]

Chọn đáp án A.

Bài 10: Cho hình chóp SABC có các mặt bên cùng tạo với đáy góc \[{60^0}\]. Tam giác ABC cân tại A, AB = a, \[\widehat {BAC} = {120^0}\]. Tính thể tích chóp SABC.

Lời giải:

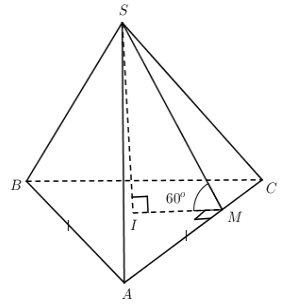
Vẽ SI ⊥ (ABC) Þ  I là tâm đường tròn nội tiếp D ABC.

Vẽ IM ⊥ AC Þ \[\widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat M = {60^0}\]

Ta có

\[\begin{array}{l}B{C^2} = A{B^2} + A{C^2} – 2AB.AC.cos{120^0}\\ \Rightarrow B{C^2} = 3{a^2} \Rightarrow BC = a\sqrt 3 \end{array}\]

Nửa chu vi tam giác ABC:

\[p = \frac{{a + a + a\sqrt 3 }}{2} = \frac{{a\left( {\sqrt 3  + 2} \right)}}{2}\]

\[\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}.a.a.\sin {120^0} = \frac{1}{2}.{a^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 {a^2}}}{4}\\r = IM = \frac{{{S_{\Delta ABC}}}}{p} = \frac{{\frac{{\sqrt 3 {a^2}}}{4}}}{{\frac{{a(\sqrt 3  + 2)}}{2}}} = \frac{{\sqrt 3 a}}{{2(\sqrt 3  + 2)}}\\h = SI = IM.\tan {60^0}\\ = r.\tan {60^0} = \frac{{\sqrt 3 a}}{{2(\sqrt 3  + 2)}}.\sqrt 3  = \frac{{3a}}{{2(\sqrt 3  + 2)}}\\{V_{SABC}} = \frac{1}{3}.h.{S_{\Delta ABC}} = \frac{1}{3}.\frac{{3a}}{{2(\sqrt 3  + 2)}}.\frac{{\sqrt 3 {a^2}}}{4} = \frac{{\sqrt 3 {a^3}}}{{8(\sqrt 3  + 2)}}.\end{array}\]

Xem thêm