Giải Toán 12 Bài 4: Phương trình bậc hai với hệ số thực

Giải bài tập Toán lớp 12 Bài 4: Phương trình bậc hai với hệ số thực

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 139 SGK Giải tích 12: Thế nào là căn bậc hai của số thực dương $a$?

Lời giải:

Căn bậc hai của một số thực dương $a$ là một số thực $b$ sao cho $b^2=a$

Câu hỏi và bài tập (trang 140 SGK Giải tích 12)
Bài 1 trang 140 SGK Giải tích 12: Tìm các căn bậc hai phức của các số sau: $-7;-8;-12;-20;-121$
Phương pháp giải:

Ta viết $-a=(-1).a=i^2.a={\left(\pm i.\sqrt{a}\right)}^2(a>0)$

Lời giải:

Căn bậc hai của $-7$ là $\pm i\sqrt{7}$;

Căn bậc hai của $-8$ là $\pm 2\sqrt{2}i$;

Căn bậc hai của $-12$ là $\pm 2\sqrt{3}i$;

Căn bậc hai của $-20$ là $\pm 2\sqrt{5}i$;

Căn bậc hai của $-121$ là $\pm 11i$

Bài 2 trang 140 SGK Giải tích 12: Giải các phương trình sau trên tập hợp số phức:

a) $-3z^2+2z-1=0$;

b) $7z^2+3z+2=0$;   

c) $5z^2-7z+11=0$ 

Phương pháp giải:

Phương trình bậc hai: $a{z}^2+bz+c=0$ $\left(a\ne 0\right)$

Bước 1: Tính: $\mathrm{\Delta }=b^2-4ac$ (hoặc ${\mathrm{\Delta }}^{\prime }=b{}^{\prime 2}-ac$).

Bước 2: 

Nếu $\mathrm{\Delta }=0$, phương trình có nghiệm kép $x=-\frac{b}{2a}$.

Nếu $\mathrm{\Delta }>0$, phương trình có hai nghiệm thực phân biệt $x=\frac{-b\pm \sqrt{\mathrm{\Delta }}}{2a}.$

Nếu $\mathrm{\Delta }<0$, gọi $\delta$ là một căn bậc hai của $\mathrm{\Delta }$. 

Phương trình có hai nghiệm phức $x_{1,2}=\frac{-b\pm \delta }{2a}$

(Với $\delta =\pm i.\sqrt{-\mathrm{\Delta }}$)

Lời giải:

a)

Ta có ${∆}^{\prime }=1^2-(-3).(-1)=1-3=-2<0.$

Ta viết: ${∆}^{\prime }=-2=2.i^2$ (Vì $i^2=-1$).

$\Rightarrow \delta =\sqrt{{\mathrm{\Delta }}^{\prime }}=\sqrt{2i^2}=\pm i\sqrt{2}$

Vậy nghiệm của phương trình là $z=\frac{1\pm i\sqrt{2}}{3}$

b)

Ta có $∆=3^2-\mathrm{4.7.2}=9-56=-47$.

Ta viết: $∆=-47=47.i^2$ (Vì $i^2=-1$).

$\Rightarrow \delta =\sqrt{\mathrm{\Delta }}=\sqrt{47i^2}=\pm i\sqrt{4}7$

Vậy nghiệm của phương trình là $z=\frac{-3\pm i\sqrt{47}}{14}$;

c)

Ta có $∆=49-\mathrm{4.5.11}=-171$.

Ta viết: $∆=-171=171.i^2$ (Vì $i^2=-1$).

$\Rightarrow \delta =\sqrt{\mathrm{\Delta }}=\sqrt{171.i^2}=\pm i\sqrt{1}71$

Vậy nghiệm của phương trình là $z=\frac{7\pm i\sqrt{171}}{10}$

Bài 3 trang 140 SGK Giải tích 12: Giải các phương trình sau trên tập hợp số phức:

a) $z^4+z^2-6=0$;

b) $z^4+7z^2+10=0$ 

Phương pháp giải:

Phương pháp giải phương trình $a{z}^4+b{z}^2+c=0\left(a\ne 0\right)$.

Bước 1: Đặt $z^2=t$, đưa về phương trình bậc hai ẩn t.

Bước 2: Giải phương trình bậc hai ẩn t: $a{t}^2+bt+c=0$.

Bước 3: Từ nghiệm t, ta giải tìm nghiệm x bằng cách tìm căn bậc hai của t.

Lời giải:

a)

Đặt $t=z^2$ , ta được phương trình $t^2+t-6=0\iff [\begin{array}{l}t=2\\ t=-3\end{array}$

Khi $t=2\Rightarrow z^2=2\Rightarrow z_{1,2}=\pm \sqrt{2}$

Khi $t=-3\Rightarrow z^2=-3\Rightarrow z_{3,4}=\pm i\sqrt{3}$

Vậy phương trình có bốn nghiệm là: $\pm \sqrt{2}$ và $\pm i\sqrt{3}$.

b)

Đặt $t=z^2$ , ta được phương trình $t^2+7t+10=0\iff [\begin{array}{l}t=-2\\ t=-5\end{array}$

Khi $t=-2\Rightarrow z^2=-2\Rightarrow z_{1,2}=\pm i\sqrt{2}$

Khi $t=-5\Rightarrow z^2=-5\Rightarrow z_{3,4}=\pm i\sqrt{5}$

Vậy phương trình có bốn nghiệm là: $\pm i\sqrt{2}$ và $\pm i\sqrt{5}$.

Bài 4 trang 140 SGK Giải tích 12: Cho $a,b,c\in \mathbb{R}$, $a\ne 0$, $z_1$ và $z_2$ là hai nghiệm của phương trình $a{z}^2+bz+c=0$

Hãy tính $z_1+z_2$ và $z_1{z}_2$ theo các hệ số $a,b,c$. 

Phương pháp giải:

+) Tính biệt thức $\mathrm{\Delta }=b^2-4ac$.

+) Chia các trường hợp của $\mathrm{\Delta }$:

TH1: $\mathrm{\Delta }\ge 0$, sử dụng kết quả của định lí Vi-et đã biết.

TH2: $\mathrm{\Delta }<0$, gọi $\delta$ là một căn bậc hai của $\mathrm{\Delta }$, suy ra các nghiệm phức của phương trình bậc hai và tính tổng, tích các nghiệm phức đó.

Lời giải:

Yêu cầu của bài toán này là kiểm chứng định lí Vi-ét đối với phương trình bậc hai trên tập số phức.

+) Trường hợp $∆\ge 0$, theo định lí vi-ét ta có: $\{\begin{array}{l}{z}_1+z_2=-\frac{b}{a}\\ z_1{z}_2=\frac{c}{a}\end{array}$

+) Trường hợp $∆<0$,  gọi $\delta$ là một căn bậc hai của $\mathrm{\Delta }$, khi đó các nghiệm của phương trình là: 

$\begin{array}{l}{z}_1=\frac{-b+\delta }{2a};z_2=\frac{-b-\delta }{2a}\\ \Rightarrow z_1+z_2=\frac{-b+\delta -b-\delta }{2a}=\frac{-b}{a}\\ z_1{z}_2=\frac{\left(-b+\delta \right)\left(-b-\delta \right)}{4a^2}=\frac{b^2-{\delta }^2}{4a^2}\\ =\frac{b^2-\left(b^2-4ac\right)}{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\end{array}$

Vậy kết quả của định lí Vi-et vẫn đúng trong trường hợp $∆<0$.

Bài 5 trang 140 SGK Giải tích 12: Cho $z=a+bi$ là một số phức. Hãy tìm một phương trình bậc hai với hệ số thực nhận $z$ và $\overline{z}$ làm nghiệm

Phương pháp giải:

Cách 1:

$z,\overline{z}$ là nghiệm của phương trình $\left(x-z\right)\left(x-\overline{z}\right)=0$.

Thay $z,\overline{z}$ và phương trình trên, đưa về đúng dạng phương trình bậc hai.

Cách 2:

Tính $S=z+\overline{z},P=z.\overline{z}$, khi đó $z,\overline{z}$ là nghiệm của phương trình $x^2-Sx+P=0$

Lời giải:

Cách 1:

Một phương trình bậc hai nhận $z$ và $\overline{z}$ làm nghiệm là

$\begin{array}{l}\left(x-z\right)\left(x-\overline{z}\right)=0\\ \iff x^2-x.\overline{z}-x.z+z.\overline{z}=0\\ \iff x^2-\left(z+\overline{z}\right)x+z.\overline{z}=0\\ \iff x^2-\left(a+bi+a-bi\right)+\left(a+bi\right)\left(a-bi\right)=0\\ \iff x^2-2ax+a^2+b^2=0\end{array}$

Vậy một phương trình bậc hai cần tìm là $x^2-2ax+a^2+b^2=0$

Cách 2:

Ta có:

$\begin{array}{l}z+\overline{z}=a+bi+a-bi=2a\\ z.\overline{z}=\left(a+bi\right)\left(a-bi\right)=a^2+b^2\end{array}$

$\Rightarrow z,\overline{z}$ là nghiệm của phương trình $x^2-2ax+a^2+b^2=0$.

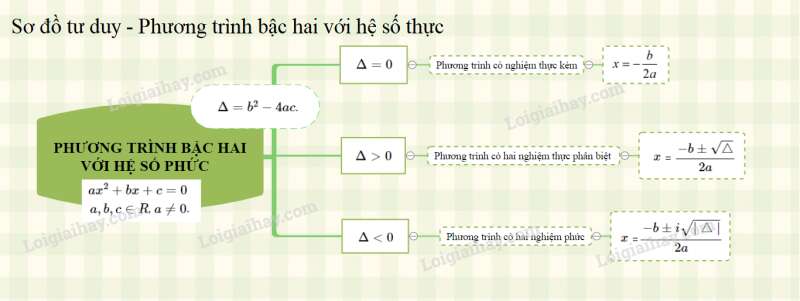
Lý thuyết Bài 4: Phương trình bậc hai với hệ số thực

Kiến thức cơ bản

– Các căn bậc hai của số thực $a<0$ là $\pm i\sqrt{|a|}$

– Xét phương trình bậc hai $a{x}^2+bx+c=0$ với $a,b,c\in R$, $a\ne 0$.

Đặt  $\mathrm{\Delta }=b^2-4ac$.

– Nếu $∆=0$ thì phương trình có một nghiệm kép (thực) $x=-\frac{b}{2a}$.

– Nếu $∆>0$ thì phương trình có hai nghiệm thực $x_{1,2}$= $\frac{-b\pm \sqrt{△}}{2a}$

– Nếu $∆<0$ thì phương trình có hai nghiệm phức $x_{1,2}$ = $\frac{-b\pm i\sqrt{|△|}}{2a}$

Nhận xét. Trên $\mathbb{C}$, mọi phương trình bậc hai đều có hai nghiệm (không nhất thiết phân biệt). Tổng quát, mọi phương trình bậc $n$, $n\in {\mathbb{N}}^{\ast }$ đều có $n$ nghiệm phức (các nghiệm không nhất thiết phải phân biệt).

Sơ đồ tư duy về phương trình bậc hai với hệ số thực