Phương pháp giải về Ứng dụng tích phân 2023 (lý thuyết và bài tập)

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

A. LÝ THUYẾT ỨNG DỤNG CỦA TÍCH PHÂN

1. Diện tích hình phẳng

Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a ; b], trục hoành và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x)|dx\)

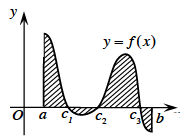
\((H)\left\{ {\begin{array}{*{20}{l}}{y = f(x)}\\{y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)

\(S = \int_a^b | f(x)|dx\)

Diện tích hình phẳng giới hạn bới đồ thị hàm số y=f(x), y=g(x) liên tục trên đoạn [a ; b] và hai đường thẳng x=a, x=b được xác định: \(S = \int_a^b | f(x) – g(x)|dx\)

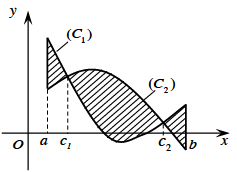
\((H)\left\{ {\begin{array}{*{20}{l}}{\left( {{C_1}} \right):y = {f_1}(x)}\\{\left( {{C_2}} \right):y = {f_2}(x)}\\{x = a}\\{x = b}\end{array}} \right.\)

\(S = \int_a^b {\left| {{f_1}(x) – {f_2}(x)} \right|} dx\)

Chú ý:

– Nếu trên đoạn [a ; b], hàm số f(x) không đổi dấu thì: \(\int_a^b | f(x)|dx = \left| {\int_a^b f (x)dx} \right|\)

– Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

– Diện tích của hình phẳng giới hạn bởi các đường x=g(y), x=h(y) và hai đường thẳng y=c, y=d được xác định: \(S = \int_c^d | g(y) – h(y)|dy\)

2. Thể tích vật thể và thể tích khối tròn xoay

a) Thể tích vật thể:

Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x \((a \le x \le b)\). Giả sử S(x) là hàm số liên tục trên đoạn [a ; b]

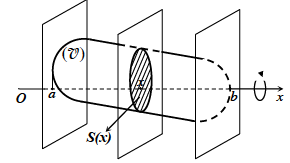
Khi đó, thể tích của vật thể B được xác định: \(V = \int_a^b S (x)dx\)

b) Thể tích khối tròn xoay:

Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), trục hoành và hai đường thẳng x=a, x=b quanh trục Ox:

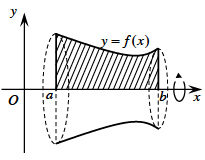
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = f(x)}\\{(Ox):y = 0}\\{x = a}\\{x = b}\end{array}} \right.\)

\({V_x} = \pi \int\limits_a^b {{{\left[ {f(x)} \right]}^2}d{\rm{x}}} \)

Chú ý:

– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường x=g(y), trục hoành và hai đường thẳng y=c, y=d quanh trục Oy:

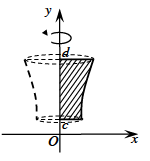
\(\left\{ {\begin{array}{*{20}{l}}{(C):y = g(y)}\\{(Oy):x = 0}\\{y = c}\\{y = d}\end{array}} \right.\)

\({V_y} = \pi \int\limits_c^d {{{\left[ {g(y)} \right]}^2}dy} \)

– Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y=f(x), y=g(x) và hai đường thẳng x=a, x=b quanh trục O x :

\(V = \pi \int_a^b {\left| {{f^2}(x) – {g^2}(x)} \right|} dx\)

3. Bài toán chuyển động của vật thể

Với bài toán chuyển động giả sử vận tốc tức thời của vật là $v\left(t\right)$ thì $v\left(t\right)=s^{\prime }\left(t\right)$

Gia tốc tức thời của vật: $a\left(t\right)=v^{\prime }\left(t\right)=s^{″}\left(t\right)$

Do đó quãng đường vật đi được từ thời điểm $t_1$ đến $t_2$ là $S=\underset{t_1}{\overset{t_2}{\int }}v\left(t\right)dt.$

Vận tốc tức thời của vật: $v\left(t\right)=\int a\left(t\right)dt$

B. BÀI TẬP VỀ ỨNG DỤNG CỦA TÍCH PHÂN

Câu 1. Viết công thức tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b) là:

A. $S=\underset{a}{\overset{b}{\int }}f\left(x\right)\text{d}x.$

B. $S=\underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|\text{d}x.$

C. $S=\underset{a}{\overset{b}{\int }}{f}^2\left(x\right)\text{d}x.$

D. $S=\pi \underset{a}{\overset{b}{\int }}\left|f\left(x\right)\right|\text{d}x.$

Câu 2. Cho đồ thị hàm số y = f(x). Diện tích S của hình phẳng (phần tô đậm trong hình dưới) là:

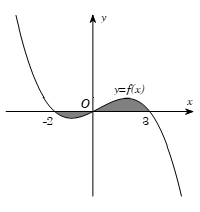
A. $S=\underset{-2}{\overset{3}{\int }}f\left(x\right)\text{d}x$

B. $S=\underset{-2}{\overset{0}{\int }}f\left(x\right)\text{d}x+\underset{0}{\overset{3}{\int }}f\left(x\right)\text{d}x$

C. $S=\underset{0}{\overset{-2}{\int }}f\left(x\right)\text{d}x+\underset{0}{\overset{3}{\int }}f\left(x\right)\text{d}x$

D. $S=\underset{-2}{\overset{0}{\int }}f\left(x\right)\text{d}x+\underset{3}{\overset{0}{\int }}f\left(x\right)\text{d}x$

Câu 3. Diện tích của hình phẳng giới hạn bởi đồ thị hai hàm số $y=x^2+2$ và $y=3x$ là:

A. $S=2$

B. $S=3$

C. $S=\frac{1}{2}$

D. $S=\frac{1}{6}$.

Câu 4. Cho (H) là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{x}^2$ và nửa đường tròn có phương trình $\text{y=}\sqrt{{\text{4-x}}^{\text{2}}}$ với -2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng?

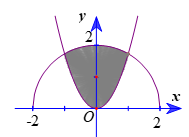
A. $\frac{2\pi +5\sqrt{3}}{3}.$

B. $\frac{4\pi +5\sqrt{3}}{3}.$

C. $\frac{4\pi +\sqrt{3}}{3}.$

D. $\frac{2\pi +\sqrt{3}}{3}.$

Câu 5: Cho hình phẳng giới hạn bởi các đường y = 3x; y = x; x = 0; x = 1 quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

Câu 6: Cho hình phẳng giới hạn bởi các đường y = x√lnx; y = 0; x = e quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

Câu 7: Cho hình phẳng giới hạn bởi các đường y = 2x²; y² = 4x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

Câu 8: Cho hình phẳng giới hạn bởi các đường  quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:

Câu 9. Gọi h(t) (cm) là mức nước trong bồn chứa sau khi bơm được t giây. Biết rằng  và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 6 giây (chính xác đến 0,01 cm)

A. 2,67 cm    

B. 2,66 cm    

C. 2,65 cm    

D. 2,68cm

Câu 10. Một hạt proton di chuyển trong điện trường có biểu thức gia tốc ( theo cm²/s) là  (với t tính bằng giây).Tìm hàm vận tốc v theo t,biết rằng khi t=0 thì v=30 (cm/s)

 

Câu 11. Một ô tô đang chạy đều với vận tốc 15 m/s thì phía trước xuất hiện chướng ngại vật nên người lái đạp phanh gấp. Kể từ thời điểm đó, ô tô chuyển động chậm dần đều với gia tốc -a m/s². Biết ô tô chuyển động thêm được 20 m thì dừng hẳn. Hỏi a thuộc khoảng nào dưới đây:

A. (3;4)

B. (4;5)

C. (5;6)

D. (6;7)

Câu 12. Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $$$v_1\left(t\right)=7t\left(\text{m/s}\right)$. Đi được 5 s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc $a=-70\left({\text{m/s}}^{\text{2}}\right)$. Tính quãng đường S (m) đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.

A. $S=87,50\left(\text{m}\right)$

B. $S=94,00\left(\text{m}\right)$

C. $S=95,70\left(\text{m}\right)$

D. $S=96,25\left(\text{m}\right)$ 

Xem thêm