Sách bài tập Toán 12 Bài 3 (Chân trời sáng tạo): Biểu thức toạ độ của các phép toán vectơ

Giải SBT Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ

Bài 1 trang 76 SBT Toán 12 Tập 1: Tìm tọa độ ba vectơ $\vec{a}, \vec{b}, \vec{c}$ thỏa mãn $\vec{a} = 2 \vec{i} + 3 \vec{j} - 5 \vec{k}$ , $\vec{b} = - 3 \vec{j} + 4 \vec{k}$ , $\vec{c} = - \vec{i} - 2 \vec{j}$ .

Lời giải:

Ta có: $\vec{a} = 2 \vec{i} + 3 \vec{j} - 5 \vec{k}$ suy ra $\vec{a}$ = (2; 3; −5).

$\vec{b} = - 3 \vec{j} + 4 \vec{k}$ suy ra $\vec{b}$ = (0; −3; 4).

$\vec{c} = - \vec{i} - 2 \vec{j}$ suy ra $\vec{c}$ = (−1; −2; 0).

Bài 2 trang 76 SBT Toán 12 Tập 1: Cho hình bình hành OABD có $\vec{O A}$ = (−1; 1; 0) và $\vec{O B}$ = (1; 1; 0) với O là gốc tọa độ. Tìm tọa độ của điểm D.

Lời giải:

Do OABD là hình bình hành với O là gốc tọa độ, nên

$\vec{O D} = \vec{A B} = \vec{O B} - \vec{O A} = (\vec{i} + \vec{j}) - (- \vec{i} + \vec{j}) = 2 \vec{i}$

Suy ra $\vec{O D}$ = (2; 0; 0) hay D(2; 0; 0).

Bài 3 trang 76 SBT Toán 12 Tập 1: Cho hình tứ diện OABC có G(3; −3; 6) là trọng tâm. Tìm tọa độ điểm A thỏa mãn $\vec{A B}$ = (1; 2; 3) và $\vec{A C}$ = (−1; 4; −2).

Lời giải:

Gọi A(a; b; c).

Có G là trọng tâm nên $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G O} = \vec{0}$

⇔ $\vec{G A} + (\vec{G A} + \vec{A B}) + (\vec{G A} + \vec{A C}) + (\vec{G A} + \vec{A O}) = \vec{0}$

⇔ $\vec{A B} + \vec{A C} + \vec{A O} = 4 \vec{A G}$

Ta có: $\vec{A B}$ = (1; 2; 3), $\vec{A C}$ = (−1; 4; −2), $\vec{A O}$ = (−a; −b; −c),

⇒ $\vec{A B} + \vec{A C} + \vec{A O}$ = (−a; 6 – b; 1 – c).

$\vec{A G}$ = (3 – a; −3 – b; 6 – c) ⇒ $4 \vec{A G}$ = (12 – 4a; −12 – 4b; 24 – 4c).

Do đó, $\{\begin{cases} - a = 12 - 4 a \\ 6 - b = - 12 - 4 a \\ 1 - c = 24 - 4 c \end{cases} \Rightarrow \{\begin{cases} a = 4 \\ b = - 6 \\ c = \frac{23}{3} \end{cases}$ ⇒ A $(4; - 6; \frac{23}{3})$

Bài 4 trang 76 SBT Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ có A(2; 4; 0), B(4; 0; 0), C(−1; 4; −7) và D'(6; 8; 10). Tìm tọa độ của điểm B’.

Lời giải:

Do ABCD.A’B’C’D’ là hình hộp nên ta có $\vec{A B} = \vec{D C} = (2; - 4; 0)$ .

Gọi D(x; y; z) suy ra $\{\begin{cases} - 1 - x = 2 \\ 4 - y = - 4 \\ - 7 - z = 0 \end{cases} \Rightarrow \{\begin{cases} x = - 3 \\ y = 8 \\ z = - 7 \end{cases}$ ⇒ D(−3; 8; −7).

Ta có: $\vec{B B^{‘}} = \vec{D D^{‘}} = (9; 0; 17)$

Gọi B'(a; b; c) suy ra $\{\begin{cases} a - 4 = 9 \\ b - 0 = 0 \\ c - 0 = 17 \end{cases} \Rightarrow \{\begin{cases} a = 13 \\ b = 0 \\ c = 17 \end{cases}$ ⇒ B'(13; 0; 17).

Bài 5 trang 76 SBT Toán 12 Tập 1: Cho điểm A(2; 2; 1). Tính độ dài đoạn thẳng OA.

Lời giải:

Ta có: A(2; 2; 1), suy ra OA = $|\vec{O A}|$ = $\sqrt{2^{2} + 2^{2} + 1^{2}}$ = 3.

Vậy OA = 3.

Bài 6 trang 76 SBT Toán 12 Tập 1: Cho điểm A(1; 2; 3). Tính khoảng cách từ A đến trục Oy.

Lời giải:

Hình chiếu của A(1; 2; 3) trên trục Oy là A'(0; 2; 0).

Khoảng cách từ A trên trục Oy là AA’ = $\sqrt{{(1 - 0)}^{2} + {(2 - 2)}^{2} + {(3 - 0)}^{2}}$ = $\sqrt{10}$

Bài 7 trang 76 SBT Toán 12 Tập 1: Cho điểm M(3; −1; 2). Tìm:

a) Tọa độ điểm M’ là điểm đối xứng của điểm M qua gốc tọa độ O.

b) Tọa độ điểm O’ là điểm đối xứng của điểm O qua điểm M.

c) Khoảng cách từ M đến gốc tọa độ.

d) Khoảng cách từ M đến mặt phẳng (Oxz).

Lời giải:

a) Tọa độ điểm M’ là điểm đối xứng của điểm M qua gốc tọa độ O là M'(−3; 1; −2).

b) O’ là điểm đối xứng của điểm O qua điểm M suy ra M là trung điểm của OO’.

Gọi O'(x; y; z) nên

$\{\begin{cases} \frac{x + 0}{2} = 3 \\ \frac{y + 0}{2} = - 1 \\ \frac{z + 0}{2} = 2 \end{cases}$ ⇒ O'(6; −2; 4).

c) Khoảng cách từ M đến gốc tọa độ là MO = $\sqrt{{(3 - 0)}^{2} + {(- 1 - 0)}^{2} + {(2 - 0)}^{2}}$ = $\sqrt{14}$ .

d) Mặt phẳng (Oxz) là y = 0.

Khoảng cách từ M đến mặt phẳng (Oxz) là d(M, (Oxz)) = $\frac{|3.0 + 1. (- 1) + 2.0|}{\sqrt{0^{2} + 1^{2} + 0^{2}}}$ = 1.

Bài 8 trang 76 SBT Toán 12 Tập 1: Cho ba điểm A(0; 2; −1), B(−5; 4; 2), C(−1; 0; 5). Tìm tọa độ trọng tâm G của tam giác ABC.

Lời giải:

Gọi G(x; y; z) là trọng tâm tam giác ABC.

Ta có:

$\{\begin{cases} x = \frac{0 + (- 5) + (- 1)}{3} = - 2 \\ y = \frac{2 + 4 + 0}{3} = 2 \\ z = \frac{- 1 + 2 + 5}{3} = 2 \end{cases}$ ⇒ G(−2; 2; 2).

Vậy G(−2; 2; 2).

Bài 9 trang 76 SBT Toán 12 Tập 1: Cho điểm M(a; b; c). Gọi A, B, C theo thứ tự là điểm đối xứng của điểm M qua các mặt phẳng (Oxy), (Oyz), (Oxz). Tìm tọa độ trọng tâm tam giác ABC.

Lời giải:

Ta có A đối xứng với M qua mặt phẳng (Oxy) nên A(a; b; −c).

B đối xứng với M qua mặt phẳng (Oyz) nên B(−a; b; c).

C đối xứng với M qua mặt phẳng (Oxz) nên C(a; −b; c).

Gọi G(x; y; z) là trọng tâm tam giác ABC.

Do đó,

$\{\begin{cases} x = \frac{a + (- a) + a}{3} = \frac{a}{3} \\ y = \frac{b + b + (- b)}{3} = \frac{b}{3} \\ z = \frac{- c + c + c}{3} = \frac{c}{3} \end{cases}$ ⇒ G $(\frac{a}{3}; \frac{b}{3}; \frac{c}{3})$ .

Bài 10 trang 76 SBT Toán 12 Tập 1: Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian Oxyz được minh họa như Hình 3. Cho biết OABC.DEFH là hình hộp chữ nhật và EMF.DNH là hình lăng trụ đứng.

Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà

a) Tìm tọa độ các điểm B, F, H.

b) Tìm tọa độ các vectơ $\vec{M E}, \vec{M F}$ .

c) Tính số đo $\hat{E M F}$ .

Lời giải:

a) Ta có OABC là hình chữ nhật nên $\vec{O A} = \vec{C B} = (6; 0; 0)$ ⇒ B(6; 4; 0).

AEFB là hình chứ nhật nên $\vec{A E} = \vec{B F} = (0; 0; 4)$ ⇒ F(6; 4; 4).

DEFH là hình chữ nhật nên $\vec{E D} = \vec{F H} = (6; 0; 0)$ ⇒ H(12; 4; 4).

b) Ta có: $\vec{M E}$ = (0; −2; −2); $\vec{M F}$ = (0; 2; −2).

c) Ta có: cos $\hat{E M F}$ = $\frac{\vec{M E} . \vec{M F}}{|\vec{M E}| . |\vec{M F}|} = \frac{0.0 + (- 2) .2 + (- 2) . (- 2)}{\sqrt{0^{2} + {(- 2)}^{2} + {(- 2)}^{2}} . \sqrt{0^{2} + 2^{2} + {(- 2)}^{2}}} = 0$ .

⇒ $\hat{E M F}$ = 90°.

Lý thuyết Biểu thức toạ độ của các phép toán vectơ

1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

Trong không gian Oxyz, cho hai vecto $\vec{a} = (x; y; z)$ và $\vec{b} = (x^{'}; y^{'}; z^{'})$ . Ta có:

$\vec{a} + \vec{b} = (x + x^{'}; y + y^{'}; z + z^{'})$
$\vec{a} - \vec{b} = (x - x^{'}; y - y^{'}; z - z^{'})$
$k \vec{a} = (k x; k y; k z)$ với k là một số thực

2. Biểu thức tọa độ của tích vô hướng

Trong không gian Oxyz, tích vô hướng của hai vecto $\vec{a} = (x; y; z)$ và $\vec{b} = (x^{'}; y^{'}; z^{'})$ được xác định bởi công thức $\vec{a} \cdot \vec{b} = x x^{'} + y y^{'} + z z^{'}$

3. Vận dụng

a) Xác định tọa độ của vecto khi biết tọa độ điểm đầu và điểm cuối

Trong không gian Oxyz, cho hai điểm $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B})$ . Ta có:

$\vec{A B} = (x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})$

b) Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác

Trong không gian Oxyz, cho ba điểm không thẳng hàng $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B}), C (x_{C}; y_{C}; z_{C})$ . Khi đó:

Tọa độ trung điểm của đoạn thẳng AB là $(\frac{x_{A} + x_{B}}{2}; \frac{y_{A} + y_{B}}{2}; \frac{z_{A} + z_{B}}{2})$
Tọa độ trọng tâm tam giác ABC là $(\frac{x_{A} + x_{B} + x_{C}}{2}; \frac{y_{A} + y_{B} + y_{C}}{2}; \frac{z_{A} + z_{B} + z_{C}}{2})$

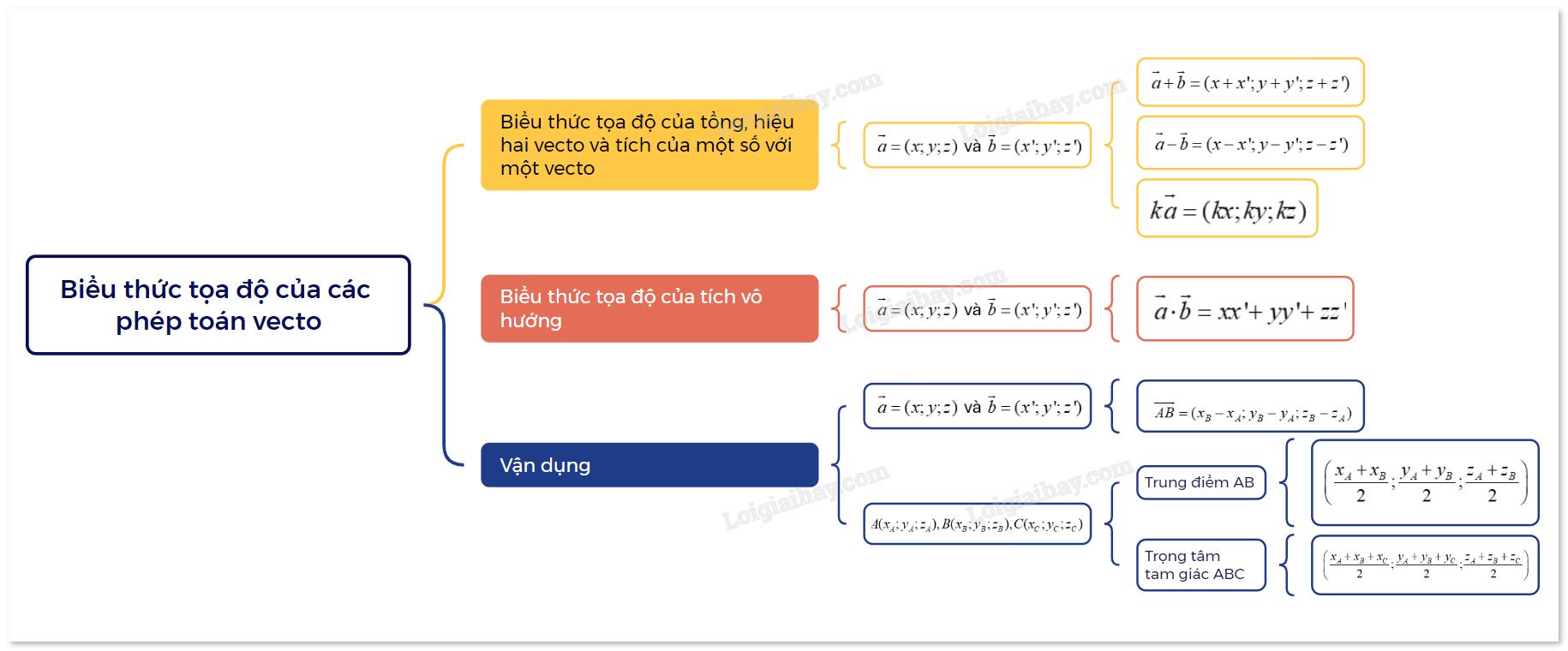
Sơ đồ tư duy Biểu thức toạ độ của các phép toán vectơ

Xem thêm các bài giải SBT Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Toạ độ của vectơ trong không gian

Bài 3: Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài tập cuối chương 3

Bài liên quan:

Leave a Comment Hủy