Giải SBT Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số
Bài 1 trang 21 SBT Toán 12 Tập 1: Tìm các đường tiệm cận của đồ thị hàm số sau:
Lời giải:
a) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận ngang y = −1.
b) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận ngang y = 1 và tiệm cận đứng x = 2.
c) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có đường tiệm cận đứng x = 1 và tiệm cận xiên là đường thẳng y = ax + b đi qua hai điểm (0; 2) và (2; 0).
Giải hệ phương trình .
Vậy đường tiệm cận xiên của đồ thị hàm số là y = −x + 2.
d) Quan sát đồ thị hàm số, ta thấy đồ thị hàm số có hai đường tiệm cận xiên.
Đường tiệm cận xiên thứ nhất y = a1x + b1 đi qua hai điểm có tọa độ (0; −3) và (4; 0).
Giải hệ phương trình, ta được: .
Do đó, đường tiệm cận xiên thứ nhất là y =
Đường tiệm cận xiên thứ hai y = a2x + b2 đi qua hai điểm có tọa độ (0; 3) và (4; 0).
Giải hệ phương trình, ta được: .
Do đó, đường tiệm cận xiên thứ hai là: y =
Bài 2 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
Lời giải:
a) Ta có: ; .
Do đó, đường thẳng x = là tiệm cận đứng của đồ thị hàm số.
; .
Do đó, đường thẳng y = là tiệm ngang của đồ thị hàm số.
b) Ta có: ; .
Do đó, đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
; .
Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
c) Ta có: ; .
Do đó, đường thẳng x = là đường tiệm cận đứng của đồ thị hàm số.
; .
Do đó, đường thẳng y = 0 là đường tiệm cận ngang của đồ thị hàm số.
Bài 3 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
Lời giải:
a)
Ta có: ; .
Do đó, đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng y = 2x + 1laf tiệm cận xiên của đồ thị hàm số.
b) Ta có: = −3x + 1 + .
; .
Do đó, đường thẳng x = 5 là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng y = −3x + 1 là tiệm cận xiên của đồ thị hàm số.
c) Ta có: = −2x + 3 –
; .
Do đó, đường thẳng x = là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng y = −2x + 3 là tiệm cận xiên của đồ thị hàm số.
Bài 4 trang 22 SBT Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
a) ;
b) y = .
Lời giải:
a) Ta có: ; .
Do đó, đường thẳng x = 1 là đường tiệm cận đứng của đồ thị hàm số.
; .
Do đó, đường thẳng x = −3 là tiệm cận đứng của đồ thị hàm số.
.
Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
b) Ta có: .
Do đó, đường thẳng y = −x là đường tiệm cận xiên của đồ thị hàm số.
.
Do đó, đường thẳng y = x là đường tiệm cận xiên của đồ thị hàm số.
Bài 5 trang 22 SBT Toán 12 Tập 1: Chi phí để làm sạch p% lượng dầu loang từ một sự cố trên biển có thể được xấp xỉ bởi công thức
C(p) = (tỉ đồng).
a) Tính chi phí để làm sạch 95%, 96%, 97%, 98% và 99% lượng dầu loang.
b) Tìm các tiệm cận của đồ thị hàm số C(p).
Lời giải:
a) Ta có: C(95) = tỉ đồng.
C(96) = tỉ đồng.
C(97) = tỉ đồng.
C(98) = tỉ đồng.
C(99) = tỉ đồng.
b) Ta có: C(p) =
; .
Do đó, đồ thị hàm số có đường tiệm cận đứng p = 100.
Bài 6 trang 22 SBT Toán 12 Tập 1: Hằng tháng, một công ty chuyên sản xuất mặt hàng A phải trả chi phí cố định là 50 triệu đồng (để thuê mặt bằng và lương nhân viên) và chi phí cho nguyên liệu là 10 000x (đồng) với x là số lượng sản phẩm A được nhập về.
a) Viết công thức tính chi phí trung bình mà công ty cần chi phí để sản xuất một sản phẩm.
b) Tìm các tiệm cận của đồ thị hàm số
Lời giải:
a) Ta có: .
b) Ta có:
; .
Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số.
;
Do đó, đường thẳng y = 10 000 là tiệm cận ngang của đồ thị hàm số.
Lý thuyết Đường tiệm cận của đồ thị hàm số
1. Đường tiệm cận đứng
| Đường thẳng gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:. |
Ví dụ: Tìm TCĐ của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số có TCĐ là x = -2.
2. Đường tiệm cận ngang
| Đường thẳng gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu hoặc . |
Ví dụ: Tìm TCN của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số f(x) có TCN là y = 3.
3. Đường tiệm cận xiên
|
Đường thẳng gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu hoặc . |
Ví dụ: Tìm TCX của đồ thị hàm số
Ta có:
Vậy đồ thị hàm số có TCX là y = x.
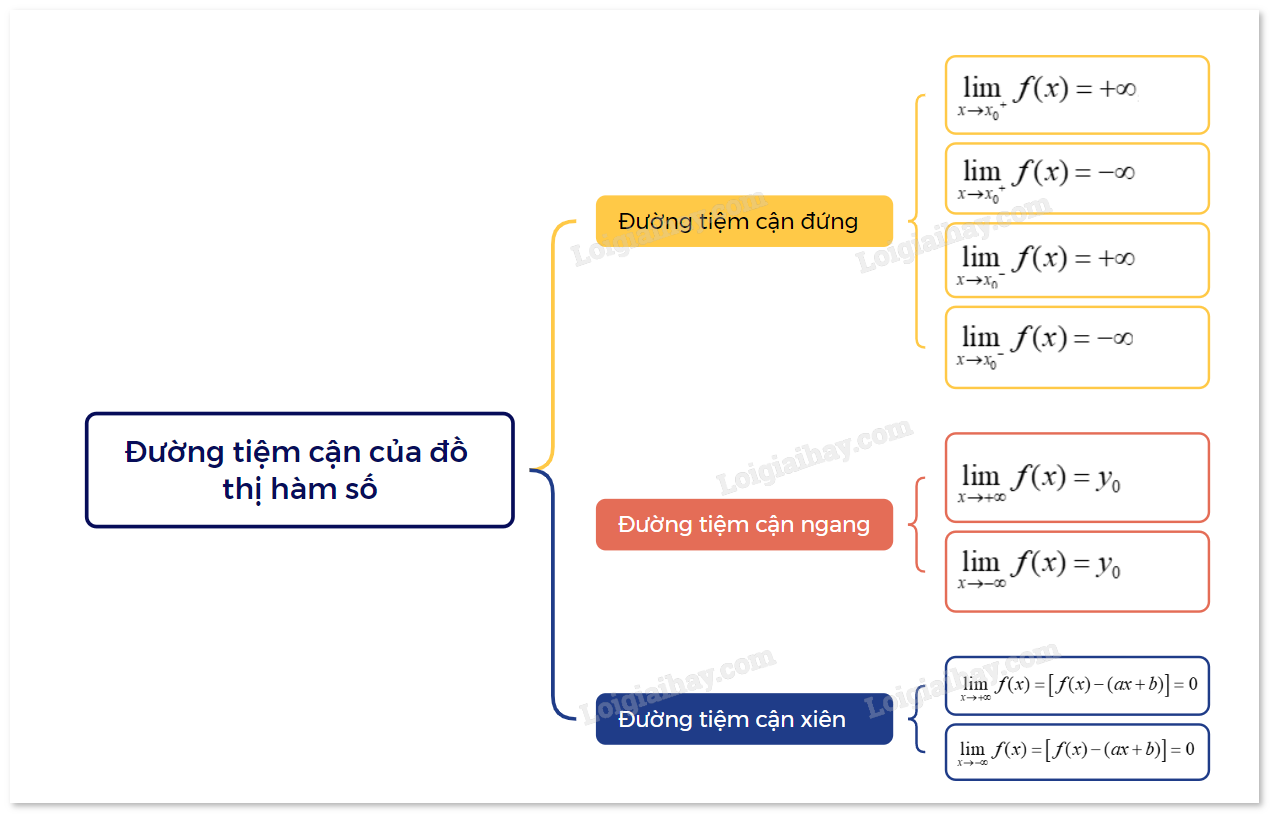
Sơ đồ tư duy Đường tiệm cận của đồ thị hàm số
Xem thêm các bài giải SBT Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài 3: Đường tiệm cận của đồ thị hàm số
Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản
Bài tập cuối chương 1
Bài 1: Vectơ và các phép toán trong không gian
Bài 2: Toạ độ của vectơ trong không gian