Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 6 Chân trời sáng tạo bản word có lời giải chi tiết:
B1: –
B2: – nhấn vào đây để thông báo và nhận giáo án.
Xem thử tài liệu tại đây: Link tài liệu
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 1
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 1)
PHẦN I. TRẮC NGHIỆM
Câu 1. Tìm số a biết: \(\frac{{ – 7}}{a} = \frac{{ – 28}}{{32}}\).
A. 4;
B. –4;
C. 8;
D. –8.
Câu 2. Cho các số thập phân –3,124; –3,105; –3,142; –3,015. Số thập phân nhỏ nhất là:
A. –3,142;
B. –3,105;
C. –3,124;
D. –3,015.
Câu 3. Quốc kỳ của nước Việt Nam là hình chữ nhật, có dài bằng \(\frac{3}{2}\) chiều rộng, nền đỏ, ở giữa có ngôi sao vàng năm cánh. Lá cờ trên cột cờ Lũng Cú – Hà Giang có chiều rộng 6 mét thì diện tích của lá cờ là:
A. 24 m2;
B. 54 m2;
C. 48 m2;
D. 30 m2.
Câu 4. Chỉ số khối của cơ thể (Body Mass Index) viết tắt là BMI thường được sử dụng để xác định tình trạng cơ thể ở mức bình thường, suy dinh dưỡng hay béo phì. Chỉ số này tính dựa trên chiều cao và cân nặng cơ thể, giúp chúng ta có cái nhìn khách quan nhất về tình trạng cân nặng bản thân. Chỉ số BMI được tính theo công thức \(BMI = \frac{m}{{{h^2}}}\) (trong đó m là khối lượng cơ thể tính theo kg, h là chiều cao cơ thể tính theo mét). Thể trạng của học sinh lớp 6 theo chỉ số BMI như sau:
BMI < 15: Gầy;
18 ≤ BMI < 23: Bình thường;
23 ≤ BMI < 30: Béo phì nhẹ;
30 ≤ BMI < 40: Béo phì trung bình;
40 ≤ BMI: Béo phì nặng.
Một bạn học sinh lớp 6 cao 150 cm, nặng 50 kg, theo em tình trạng cơ thể bạn ở mức nào?
A. Bình thường;
B. Béo phì trung bình;
C. Béo phì nhẹ; .
D. Béo phì nặng.
Câu 5. Trong đợt thực hiện kế hoạch nhỏ của trường THCS A, khối 6 của trường đã thu được 1035 kg giấy vụn. Trong đó lớp 6A thu được 105 kg. Tỉ số phần trăm số giấy vụn mà lớp 6A đã thu được so với khối 6 của trường (làm tròn đến chữ số thập phân thứ nhất) là:
A. 10,1%;
B. 10,2%;
C. 10,4%;
D. 10%.
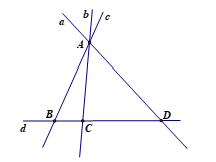
Câu 6. Cho hình vẽ sau. Các đoạn thẳng có độ dài bằng nhau là:
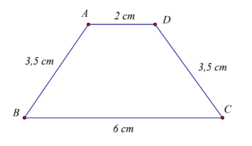
A. AD và AB;
B. AD và BC;
C. AD và DC;
D. DC và AB.
Câu 7. Số đo của góc mAn ở hình vẽ dưới đây là:
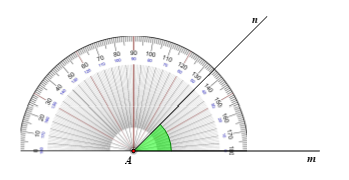
A. 40°;
B. 45°;
C. 130°;
D. 135°.
Câu 8. Trong các hình đồng hồ sau, hình nào có góc tạo bởi hai kim đồng hồ nào là góc nhọn?
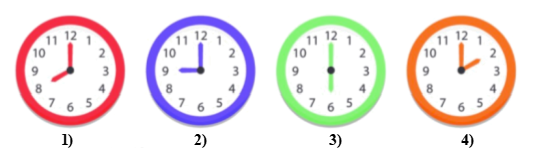
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 9. Hình nào sau đây có trục đối xứng đồng thời có tâm đối xứng?
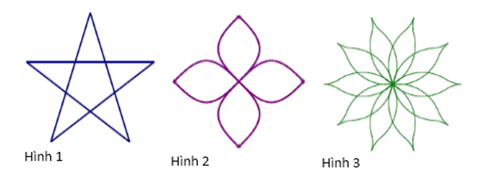
A. Hình 1 và Hình 2;
B. Hình 1 và Hình 3;
C. Hình 2 và Hình 3;
D. Hình 1, Hình 2, Hình 3.
Câu 10. Số hình không có trục đối xứng trong số 6 hình dưới đây là:

A. 1;
B. 2;
C. 3;
D. 4.
Câu 11. Trong hộp có bốn viên bi, trong đó có một viên bi màu vàng, một viên bi màu trắng, một viên bi màu đỏ và một viên bi màu tím. Lấy ngẫu nhiên một viên bi trong hộp. Hỏi có bao nhiêu kết quả xảy ra đối với màu của viên bi được lấy ra?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 12. Một xạ thủ bắn 30 mũi tên vào một tấm bia thì được 23 lần trúng. Xác suất xạ thủ bắn trúng tấm bia là:
A. \(\frac{{23}}{{30}}\);
B. \(\frac{{23}}{{53}};\)
C. \(\frac{{30}}{{23}};\)
D. \(\frac{{30}}{{53}}.\)
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(2\frac{3}{4} – \left( {\frac{1}{7} + 1\frac{3}{4}} \right)\)
b) \(\frac{7}{{ – 25}} + \frac{{ – 18}}{{25}} + \frac{4}{{23}} + \frac{5}{7} + \frac{{19}}{{23}}\)
c) \[\frac{{ – 1}}{4}.\left( {12\frac{3}{4} – 7,75} \right) – 25\% .3\frac{1}{2}\]
Bài 2. Tìm x biết
a) \(\frac{{ – 4}}{5}x = \frac{4}{7}\)
b) \( – \frac{2}{3}x + \frac{1}{5} = \frac{1}{{10}}\)
c) \(\left[ {22,5 – \left( {\frac{2}{3} + \frac{4}{5}} \right)x} \right]:\frac{2}{3} – 75\% = 0\)
Bài 3. Một lớp có 45 học sinh. Số học sinh trung bình bằng \(\frac{7}{{15}}\) số học sinh cả lớp. Số học sinh khá bằng \(\frac{5}{8}\) số học sinh còn lại. Tính số học sinh giỏi?
Bài 4. Kiểm tra thị lực của học sinh một trường THCS thu được kết quả theo bảng sau:
|
Khối |
Số học sinh được kiểm tra |
Số học sinh bị tật khúc xa (cận thị, viễn thị, loạn thị) |
|
6 |
180 |
19 |
|
7 |
190 |
28 |
|
8 |
210 |
36 |
|
9 |
200 |
42 |
a) Tính số học sinh được kiểm tra thị lực và số học sinh bị tật khúc xạ của từng khối trường đó.
b) Tính xác suất thực nghiệm của sự kiện “học sinh bị tật khúc xạ” của khối lớp 6.
Bài 5. Cho C là trung điểm của đoạn thẳng AB, O là trung điểm của đoạn thẳng BC. Tính độ dài đoạn thẳng AC, BC và OB biết rằng AB = 8 cm.
Bài 6. Tìm số nguyên n sao cho \(\left( {3n + 24} \right) \vdots \left( {n – 4} \right)\).
……………………………………..
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 2
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 2)
PHẦN I. TRẮC NGHIỆM
Câu 1. Phân số nhỏ nhất trong các phân số \(\frac{3}{{ – 8}};\frac{{ – 5}}{8};\frac{{ – 1}}{8};\frac{7}{{ – 8}}\) là:
A. \(\frac{3}{{ – 8}};\)
B. \(\frac{{ – 5}}{8};\)
C. \(\frac{{ – 1}}{8};\)
D. \(\frac{7}{{ – 8}}.\)
Câu 2. Kết quả của phép tính (–14,3) : (–2,5) là:
A. –57,2;
B. –5,72;
C. 5,72 .
D. 57,2 .
Câu 3. Viết hỗn số \(2\frac{8}{7}\) dưới dạng số thập phân (làm tròn đến chữ số thập phân thứ nhất).
A. 3,1;
B. 3,14;
C. 3,15;
D. 3,2.
Câu 4. Tại một cửa hàng, một chú gấu bông có giá 300 000 đồng. Nhân ngày Quốc tế Thiếu nhi, cửa hàng thực hiện giảm giá 45% các mặt hàng. Hỏi giá bán của chú gấu bông sau khi đã giảm là bao nhiêu?
A. 135 000 đồng;
B. 235 000 đồng;
C. 155 000 đồng;
D. 165 000 đồng.
Câu 5. Bạn An có 120 viên bi trong đó có 30 viên bi đỏ, 25 viên bi xanh, 40 viên bi vàng, còn lại là bi trắng. Hỏi số bi trắng chiếm bao nhiêu phần tổng số bi?
A. \(\frac{5}{{12}}\);
B. \(\frac{5}{{24}}\);
C. \(\frac{5}{6}\);
D. \(\frac{1}{4}\).
Câu 6. Trong các hình sau, điểm O là tâm đối xứng của hình nào?
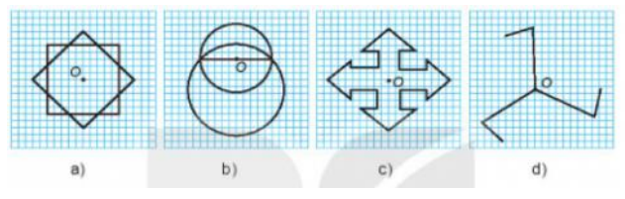
A. Hình a, b;
B. Hình c, d;
C. Hình a, c;
D. Hình a, b và c.
Câu 7. Biết khi hai kim đồng hồ chỉ vào hai số liên tiếp nhau thì góc giữa hai kim đồng hồ là 30°. Góc tạo bởi kim phút và kim giờ tại thời điểm 5 giờ là:
A. 30°;
B. 70°;
C. 150°;
D. 180°.
Câu 8. Cho hình vẽ dưới đây. Có bao nhiêu cặp đường thẳng song song?
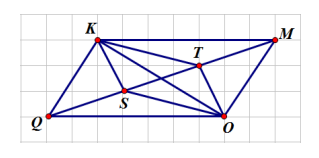
A. 3;
B. 4;
C. 5;
D. 6.
Câu 9. Trong các hình sau, hình nào không có trục đối xứng?

A. Hình Quốc huy Việt Nam;
B. Hình Huy hiệu Đội TNTP HCM;
C. Hình Huy hiệu Đoàn TNCS HCM;
D. Hình lá cờ Tổ quốc Việt Nam.
Câu 10. Số đo của góc mAn ở hình vẽ dưới đây là:
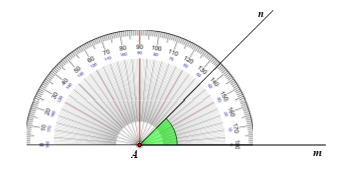
A. 40°;
B. 45°;
C. 130°;
D. 135°.
Câu 11. Chọn phát biểu đúng trong các phát biểu sau:
A. Một sự kiện có thể xảy ra hoặc không thể xảy ra tùy thuộc vào kết quả của phép thử nghiệm đó.
B. Một sự kiện có thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
C. Một sự kiện đồng thời có thể xảy ra hoặc không thể xảy ra trong phép thử nghiệm đó.
D. Một sự kiện có thể xảy ra hoặc không thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
Câu 12. Tung đồng xu 50 lần thì thấy mặt S xuất hiện 19 lần. Số lần xuất hiện mặt N là:
A. 19;
B. 50;
C. 31;
D. 69.
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) (–4,44 + 60 – 5,56) : (1,2 – 0,8);
b) \(\frac{2}{{11}} – \frac{3}{8} + \frac{4}{{11}} – \frac{6}{{11}} – \frac{5}{8}\);
c) \(\frac{5}{{39}}\,\, \cdot \,\left( {\,7\frac{4}{5}\,\, \cdot \,1\frac{2}{3}\,\, + \,\,8\frac{1}{3}\, \cdot \,7\frac{4}{5}\,} \right)\);
Bài 2. Tìm x biết:
a) \(2\frac{2}{3}:x = 2\frac{1}{{12}}:( – 0,06)\);
b) \(\frac{3}{4} – \left( {4\frac{1}{2} + 3x} \right) = – 1\);
c) \(\left( {4,5 – 2x} \right).\frac{{11}}{7} = \frac{{11}}{{14}}\)
Bài 3. Bạn An làm một số bài toán trong ba ngày, ngày đầu bạn làm được \(\frac{2}{3}\) tổng số bài, ngày thứ hai bạn làm được 20% tổng số bài, ngày thứ ba bạn làm nốt 2 bài. Hỏi trong ba ngày bạn An làm được bao nhiêu bài toán?
Bài 4. Trong một hộp kín có một số quả bóng màu xanh, màu đỏ, màu tím, vàng. Trong một trò chơi, người chơi được lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. Minh thực hiện 100 lần và được kết quả sau:
|
Màu |
Số lần |
|
Xanh |
25 |
|
Đỏ |
23 |
|
Tím |
30 |
|
Vàng |
22 |
Hãy tìm xác suất của thực nghiệm của các sự kiện sau:
a) Minh lấy được quả bóng màu xanh;
b) Quả bóng được lấy ra không là màu đỏ.
Bài 5. a) Vẽ góc xOy có số đo bằng 105°. Góc xOy là góc nhọn, góc vuông hay góc tù?
b) Trên Ox lấy hai điểm A, B sao cho OA = 4 cm, OB = 6 cm. Gọi \(M\) là trung điểm của đoạn thẳng AB. Tính AM.
Bài 6. Tìm số nguyên n sao cho \(\left( {3n + 24} \right) \vdots \left( {n – 4} \right)\).
……………………………………..
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 3
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 3)
PHẦN I. TRẮC NGHIỆM
Câu 1. Năm 2020 do dịch COVID-19 nên nhiều nhà máy gặp khó khăn, một nhà máy may mặc trong tháng 2/2020 có ghi số dư là –2,3 tỉ đồng. Sang tháng 3/2020 do chuyển hướng sản xuất sang khẩu trang xuất khẩu nên số dư là 0,35 tỉ đồng. Số tiền mà nhà máy tăng được trong tháng 3/2020 là:
A. 1,95 tỉ đồng;
B. – 2,65 tỉ đồng;
C, 2,65 tỉ đồng;
D. – 1,95 tỉ đồng.
Câu 2. Trong các phân số \(\frac{{ – 7}}{{42}};\frac{{12}}{{18}};\frac{3}{{ – 18}};\frac{{ – 9}}{{54}};\frac{{ – 10}}{{ – 15}};\frac{{14}}{{20}}\) thì có bao nhiêu cặp phân số bằng nhau?
A. 2;
B. 3;
C. 4;
D. 5.
Câu 3. Bác Hoa gửi tiết kiệm 15 000 000 đồng với lãi suất 0,6% một tháng thì sau một tháng bác thu được số tiền lãi là:
A. 9 000 đồng;
B. 15 090 000 đồng;
C. 90 000 đồng;
D. 900 000 đồng.
Câu 4. Bạn An có 120 viên bi trong đó có 30 viên bi đỏ, 25 viên bi xanh, 40 viên bi vàng, còn lại là bi trắng. Hỏi số bi đỏ chiếm bao nhiêu phần tổng số bi?
A. \(\frac{5}{{12}}\);
B. \(\frac{5}{{24}}\);
C. \(\frac{5}{6}\);
D. \(\frac{1}{4}\).
Câu 5. Biết \[\frac{2}{5}\] quả sầu riêng nặng 0,45 kg. Quả sầu riêng đó nặng là:
A. 1,8 kg;
B. 1,125 kg;
C. 2,25 kg;
D. 0,9 kg.
Câu 6. Cho hình vẽ biết CD = DE = 3 cm.
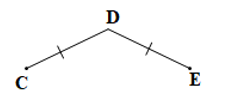
Khi đó:
A. CE = 3 cm;
B. D là trung điểm của EC;
C. D nằm giữa hai điểm C và E.
D. D không là trung điểm của EC.
Câu 7. Có bao nhiêu biển báo giao thông dưới đây có tâm đối xứng?
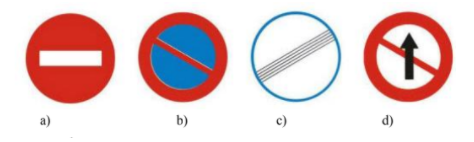
A. 1 biển báo;
B. 2 biển báo;
C. 3 biển báo;
D. 4 biển báo.
Câu 8. Cho các hình sau:
(I) Hình thoi; (II) Hình thang cân; (III) Hình vuông; (IV) Hình tròn; (V) Hình ngôi sao 5 cánh.
Trong các hình trên, hình nào không có tâm đối xứng?
A. (I) và (V);
B. (II) và (V);
C. (II) và (III);
D. (II), (III) và (V).
Câu 9. Trong các hình đồng hồ sau, hình nào có góc tạo bởi hai kim đồng hồ nào là góc vuông?
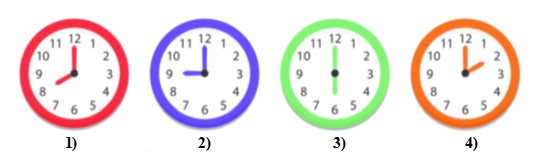
A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 10. Góc xOt dưới đây có số đo là bao nhiêu độ và là góc nhọn hay góc tù?
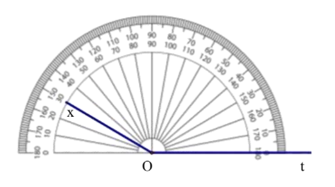
A. 150° và là góc nhọn;
B. 30° và là góc nhọn;
C. 150° và là góc tù;
D. 30° và là góc tù.
Câu 11. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm dưới 5 là:
A. 1;
B. 2;
C. 3;
D. 11.
Câu 12. Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng vàng; các quả bóng có kích thước và khối luợng như nhau. Mỗi lần bạn Mai lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Nếu bạn Mai lấy 15 lần lấy bóng liên tiếp, có 3 lần xuất hiện màu đỏ thì xác suất thực nghiệm xuất hiện màu đỏ là:
A. \(\frac{1}{{15}}\);
B. \(\frac{3}{{15}}\);
C. \(\frac{1}{3}\);
D. \(\frac{4}{{15}}\).
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{3}{4} – \frac{{16}}{{32}} + \frac{4}{{ – 3}}\)
b) \(\left( {\frac{1}{9} – \frac{9}{{23}}} \right) + \left( { – \frac{{14}}{{23}} – \frac{1}{2}} \right) + \frac{8}{9}\)
c) \(\left( {0,125 + 40\% – \frac{3}{{40}}} \right):\left[ {11\frac{3}{7} + 8\frac{1}{2} – \left( {\frac{{13}}{{12}} – 5\frac{4}{7}} \right)} \right]\)
Bài 2. Tìm x biết:
a) 31,5 – x = (18,6 – 12,3) : 3
b) \[4.\left( {\frac{{ – 5}}{6}} \right) – x = \frac{7}{{12}} + \frac{{ – 1}}{3}\]
c) \(\frac{1}{2} – \frac{1}{2}x = \frac{2}{3}\)
Bài 3. Một lớp có 40 học sinh gồm ba loại: giỏi, khá, trung bình. Số học sinh giỏi chiếm \(\frac{1}{5}\) số học sinh cả lớp. Số học sinh trung bình bằng \(\frac{3}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại.
b) Tính tỉ số % học sinh mỗi loại.
Bài 4. Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Khi gieo xúc xắc có 6 mặt thì có những kết quả nào có thể xảy ra?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện gieo được mặt có 3 chấm;
Bài 5. Cho bốn điểm A, B, C, D cùng nằm trên một đường thẳng sao cho B nằm giữa hai điểm A và C, C nằm giữa hai điểm B và D. Biết rằng AC = 5 cm, BC = 3 cm và AD = 7cm.
a) Chứng tỏ rằng AB = CD.
b) Vẽ tia Ax sao cho góc xAD có số đo bằng 110°. Góc xAD là loại góc gì?
Bài 6. Tính nhanh: \[A = \frac{{10}}{{3.7}} – \frac{5}{{7.12}} – \frac{7}{{12.19}} – \frac{5}{{19.24}}\].
……………………………………..
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 4
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 4)
PHẦN I. TRẮC NGHIỆM
Câu 1. Cho \(\frac{{12}}{x} = \frac{{ – 2}}{3}\). Số x thích hợp là:
A. –18;
B. –4;
C. 4;
D. 18.
Câu 2. Số –1,023 là:
A. Số thập phân;
B. Phân số;
C. Số tự nhiên;
D. Cả A, B, C đều sai.
Câu 3. Tỷ số % của \(\frac{3}{{15}}\) và \(\frac{4}{{20}}\) là:
A. 100% ;
B. 12% ;
C. 30% ;
D. 15%.
Câu 4. Diện tích đất trồng trọt của một xã là khoảng 81,5 ha. Vụ hè thu năm nay, xã này dự định dùng \(\frac{5}{7}\) diện tích này để trồng lúa. Tính diện tích trồng lúa vụ thu hè của xã (làm tròn kết quả chữ số thập phân thứ ba):
A. 58,214 ha;
B. 58,210 ha;
C. 58,215 ha;
D. 58,220 ha.
Câu 5. So sánh \(a = \frac{{2525}}{{2626}}\) với \(b = \frac{{20212021}}{{20222022}}\)
A. a < b;
B. a = b;
C. a > b;
D. a ≥ b.
Câu 6. Trong các phát biểu sau, phát biểu nào sai?
A. Đường tròn có tâm là tâm đối xứng;
B. Tam giác đều có một tâm đối xứng;
C. Chữ cái in hoa I có một tâm đối xứng;
D. Hình bình hành nhận giao điểm của hai đường chéo làm tâm đối xứng.
Câu 7. Hình vẽ dưới đây có bao nhiêu đoạn thẳng?
A. 3;
B. 4;
C. 5;
D. 6.
Câu 8. Khẳng định đúng là
A. Góc có số đo 80° là góc tù;
B. Góc có số đo 100° là góc nhọn;
C. Góc có số đo 120° là góc vuông;
D. Góc có số đo 140° là góc tù.
Câu 9. Số hình không có trục đối xứng trong số 6 hình dưới đây là:

A. 4;
B. 3;
C. 2;
D. 1.
Câu 10. Trong các hình đồng hồ sau, hình nào có góc tạo bởi hai kim đồng hồ nào là góc tù?
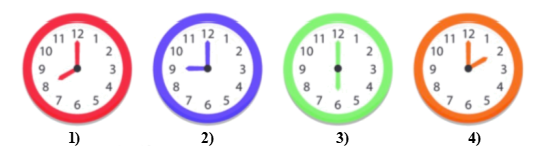
A. Hình 3;
B. Hình 1;
C. Hình 4;
D. Hình 2.
Câu 11. Cuối tuần, Tuấn được bố mẹ cho phép đến nhà Khang chơi nhưng con đường Tuấn thường đi đang sửa chữa nên Tuấn phải đi đường khác. Giữa đường có 4 ngã rẽ, nhưng chỉ có một ngã dẫn đến nhà Khang, Tuấn không nhớ cần rẽ ngã nào. Có mấy kết quả có thể khi Tuấn chọn ngã rẽ? Liệt kê.
A. 2 kết quả: đến được nhà Khang, không đến được nhà Khang.
B. 3 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang.
C. 4 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang, bị lạc đường.
D. Tất cả đều sai.
Câu 12. Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng vàng; các quả bóng có kích thước và khối luợng như nhau. Mỗi lần bạn Yến lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Nếu bạn Yến lấy 15 lần lấy bóng liên tiếp, có 5 lần xuất hiện màu xanh thì xác suất thực nghiệm xuất hiện màu xanh là:
A. \(\frac{1}{{15}}\);
B. \(\frac{3}{{15}}\);
C. \(\frac{1}{3}\);
D. \(\frac{4}{{15}}\).
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
b) \(\frac{{ – 5}}{7} \cdot \frac{2}{{11}} + \frac{{ – 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
c) \(1\frac{{13}}{{15}}.0,75 – \left( {\frac{8}{{15}} + 25\% } \right)\)
Bài 2. Tìm x biết:
a) \(\frac{2}{3}.x + \frac{1}{2} = \frac{1}{{10}}\)
b) x : 2,2 = (28,7 – 13,5).2;
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
Bài 3. Hoa làm một số bài toán trong ba ngày. Ngày đầu bạn làm được \(\frac{1}{3}\) số bài. Ngày thứ hai bạn làm được \(\frac{3}{7}\) số bài còn lại . Ngày thứ ba bạn làm nốt 8 bài. Trong ba ngày bạn Hoa làm được bao nhiêu bài?
Bài 4. Cho bảng thống kê phỏng vấn thể loại phim yêu thích của các bạn học sinh sau.
|
Thể loại phim |
Hành động |
Khoa học viễn tưởng |
Hoạt Hình |
Hài |
|
Số lượng bạn yêu thích |
7 |
8 |
15 |
9 |
a) Cho biết có bao nhiêu bạn tham gia phỏng vấn?
b) Cho biết thể loại phim nào được yêu thích nhất?
c) Tính xác suất của sự kiện chọn ra một bạn học sinh ngẫu nhiên thích phim khoa học viễn tưởng.
Bài 5. Cho hình vẽ sau:
a) Có bao nhiêu đường thẳng đi qua điểm A? Kể tên.
b) Điểm C nằm trong góc nào?
c) Trên hình vẽ biết điểm C nằm giữa hai điểm B và D. Cho BC = 1 cm, CD = 3 cm. Hỏi điểm C có phải là trung điểm của BD không? Tính BD.
Bài 6. Chứng minh \(\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{36}} + \frac{1}{{64}} + \frac{1}{{100}} + \frac{1}{{144}} + \frac{1}{{196}} < \frac{1}{2}\).
……………………………………..
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 5
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 5)
PHẦN I. TRẮC NGHIỆM
Câu 1. Hỗn số \(5\frac{3}{4}\) được viết dưới dạng phân số:
A. \(\frac{{15}}{4}\);
B. \(\frac{2}{{23}}\);
C. \(\frac{{19}}{4}\);
D. \(\frac{{23}}{4}\).
Câu 2. Biết tỉ số phần trăm của nước trong dưa chuột là 92,8%. Lượng nước trong 10 kg dưa chuột là:
A. 12,88 kg;
B. 9,28 kg;
C. 10,76 kg;
D. 3,8 kg.
Câu 3. Sau một thời gian gửi tiết kiệm, người gửi đi rút tiền và nhận được 320 000 đồng tiền lãi. Biết rằng số lãi bằng \(\frac{1}{{25}}\) số tiền gửi tiết kiệm. Tổng số tiền người đó nhận được là:
A. 8 000 000 đồng;
B. 8 320 000 đồng;
C. 7 680 000 đồng;
D. 2 400 000 đồng.
Câu 4. So sánh \(a = \frac{5}{{ – 7}}\) vả \(b = – \frac{7}{{11}}\).
A. a > b;
B. a ≥ b;
C. a < b;
D. a = b.
Câu 5. Trong chương trình khuyến mại giảm giá 20%, hộp sữa bột có giá là 840 000 đồng. Như vậy khi mua một hộp sữa với giá niêm yết người mua cần phải trả số tiền là:
A. 168 000 đồng;
B. 672 000 đồng;
C. 4 200 000 đồng;\(\quad \)
D. 1 050 000 đồng.
Câu 6. Trong các hình sau có bao nhiêu hình có trục đối xứng đồng thời có tâm đối xứng?

A. 1;
B. 2;
C. 3;
D. 4.
Câu 7. Trong các hình sau đây, hình nào không có trục đối xứng (mỗi hình là một từ)?

A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 8. Đường thẳng a chứa những điểm nào?
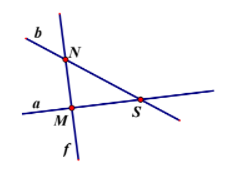
A. M và N;
B. M và S;
C. N và S;
D. M, N và S.
Câu 9. Khẳng định sai là
A. Góc có số đo 90° là góc vuông;
B. Góc có số đo 130° là góc tù;
C. Góc có số đo 100° là góc nhọn;
D. Góc có số đo 170° là góc tù.
Câu 10. Trong hình vẽ dưới đây có bao nhiêu bộ ba điểm thẳng hàng?
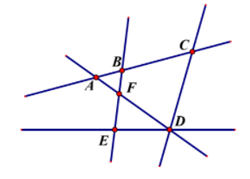
A. 5 bộ;
B. 4 bộ;
C. 3 bộ;
D. 1 bộ.
Câu 11. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm 8, điểm 9 là:
A. 11;
B. 6;
C. 7;
D. 12.
Câu 12. Bạn Hùng tung đồng xu cân đối một số lần được kết quả sau:
|
Sự kiện |
Hai đồng ngửa |
Một đồng ngửa, một đồng sấp |
Hai đồng sấp |
|
Số lần |
32 |
48 |
20 |
Xác suất thực nghiệm của sự kiện có hai đồng xu sấp là:
A. \(\frac{{32}}{{100}};\)
B. \(\frac{1}{5}\);
C. \(\frac{{12}}{{25}};\)
D. \(\frac{{13}}{{25}};\)
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \[\frac{3}{{13}}.\frac{6}{{11}} + \frac{9}{{13}}.\frac{3}{{11}} – \frac{3}{{13}}.\frac{4}{{11}}\]
b) 5,34 . 26,15 + 5,34 .(–126,15).
c) \(1,4.\frac{{15}}{{49}} – \left( {\frac{4}{5} + \frac{2}{3}} \right):2\frac{1}{5};\)
Bài 2. Tìm x biết:
a) \[x – \frac{1}{5} = \frac{7}{{11}}.\frac{3}{{21}};\]
b) \(\frac{x}{5} = \frac{2}{3};\)
c) \(\frac{{ – 2}}{3} – \frac{1}{3}\left( {2x – 5} \right) = \frac{3}{2}\)
Bài 3. Ba lớp 6 trường THPT có 240 học sinh. Số học sinh lớp 6A chiếm 35% so với học sinh của khối. Số học sinh lớp 6B bằng \(\frac{{20}}{{21}}\) số học sinh lớp 6A. Còn lại là học sinh lớp 6C. Tính số học sinh của mỗi lớp?
Bài 4. Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Khi gieo xúc xắc có 6 mặt thì có những kết quả nào có thể xảy ra?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện gieo được mặt có 2 chấm;
Bài 5. Cho đoạn thẳng AB = 5 cm và M là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng AM và MB.
2. Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây:
a) Vẽ \(\widehat {mOn}\) không phải là góc bẹt.
b)Vẽ \(\widehat {xOy}\) là góc nhọn có điểm A nằm trong góc đó.
Bài 6. Tính nhanh \(A = \frac{1}{{15}} + \frac{1}{{35}} + … + \frac{1}{{2499}}\).
……………………………………..
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 6
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 6)
PHẦN I. TRẮC NGHIỆM
Câu 1. Số –1,023 là:
A. Số thập phân;
B. Phân số;
C. Số tự nhiên;
D. Cả A, B, C đều sai.
Câu 2. Phân số lớn nhất trong các phân số \(\frac{4}{{ – 9}};\frac{{ – 2}}{9};\frac{{ – 7}}{9};\frac{5}{{ – 9}}\) là:
A. \(\frac{4}{{ – 9}};\)
B. \(\frac{{ – 2}}{9};\)
C. \(\frac{{ – 7}}{9};\)
D. \(\frac{5}{{ – 9}}\).
Câu 3. Một khu vườn hình chữ nhật có chiều dài 5,5m. Chiều rộng bằng \(\frac{2}{5}\) chiều dài. Diện tích khu vườn là:
A. 7,7 m2;
B. 12,1 m2;
C. 15,4 m2;
D. 2,2 m2.
Câu 4. Biết rằng trong chuối chín cứ 100 gam chuối có chứa 0,3% chất béo; 0,42% kali. Hỏi một quả chuối nặng 120 gam thì tổng khối lượng chất béo và kali có trong đó là:
A. 0,846 g;
B. 0,864 g;
C. 86,4 g;
D. 8,64 g.
Câu 5. Sáng chủ nhật mẹ nhờ Lan đi siêu thị mua 1 kg cà chua và 2 kg khoai tây. Biết rằng 1 kg cà chua giá 25 000 đồng và 1 kg khoai tây giá 18 000 đồng. Khi thanh toán Lan phải trả số tiền thuế gia tăng VAT (được tính bằng 10% tổng số tiền hàng). Vậy em hãy ước lượng số tiền Lan phải trả là:
A. 43 000 đồng;
B. 81 000 đồng;
C. 70 000 đồng;
D. 50 000 đồng.
Câu 6. Hình vẽ dưới đây có bao nhiêu đoạn thẳng?
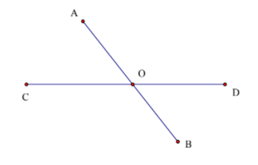
A. 3;
B. 4;
C. 5;
D. 6.
Câu 7. Góc xOt dưới đây có số đo là bao nhiêu độ và là góc nhọn hay góc tù?
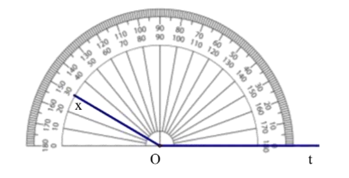
A. 150° và là góc nhọn;
B. 30° và là góc nhọn;
C. 150° và là góc tù;
D. 30° và là góc tù.
Câu 8. Trong các chữ cái F, G, I, L chữ nào có trục đối xứng?
A. F;
B. G;
C. I;
D. L.
Câu 9. Trong các hình sau có bao nhiêu hình có trục đối xứng đồng thời có tâm đối xứng?

A. 1;
B. 2;
C. 3;
D. 4.
Câu 10. Cho các hình sau:
(I) Hình thoi; (II) Hình thang cân; (III) Hình vuông; (IV) Hình tròn; (V) Hình ngôi sao 5 cánh.
Trong các hình trên, hình nào không có tâm đối xứng?
A. (I) và (V);
B. (II) và (V);
C. (II) và (III);
D. (II), (III) và (V).
Câu 11. Gieo một con xúc xắc, sự kiện “số chấm xuất hiện là số lẻ” có bao nhiêu kết quả xảy ra?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 12. Một hộp có 1 quả bóng xanh, 1 quả bóng đỏ và 1 quả bóng vàng; các quả bóng có kích thước và khối luợng như nhau. Mỗi lần bạn Yến lấy ngẫu nhiên một quả bóng trong hộp, ghi lại màu của quả bóng lấy ra và bỏ lại quả bóng đó vào hộp. Nếu bạn Yến lấy 15 lần lấy bóng liên tiếp, có 5 lần xuất hiện màu xanh thì xác suất thực nghiệm xuất hiện màu xanh là:
A. \(\frac{1}{{15}}\);
B. \(\frac{3}{{15}}\);
C. \(\frac{1}{3}\);
D. \(\frac{4}{{15}}\).
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{3}{4} – \frac{{16}}{{32}} + \frac{4}{{ – 3}}\)
b) \(\frac{{ – 2}}{{17}} + \frac{{15}}{{19}} + \frac{{ – 15}}{{17}} + \frac{{15}}{{23}} + \frac{4}{{19}}\)
c) \(\left( { – 2,4 + \frac{1}{3}} \right):3\frac{1}{{10}} + 75\% :1\frac{1}{2}\)
Bài 2. Tìm x biết
a) \(x:\frac{2}{3} – \frac{1}{2} = 1\frac{3}{4}\)
b) \(\frac{{33}}{4} – \frac{1}{2}:2x = 8\)
c) \(\left( {1\frac{2}{3} – 2x} \right).75\% – 2 = \frac{{13}}{{16}}\)
Bài 3. Một lớp có 40 học sinh gồm ba loại : giỏi, khá, trung bình. Số học sinh giỏi chiếm \(\frac{1}{5}\) số học sinh cả lớp. Số học sinh trung bình bằng \(\frac{3}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại.
b) Tính tỉ số % học sinh mỗi loại.
Bài 4. Kết quả về thực nghiệm điều tra loại trái cây yêu thích của các bạn học sinh lớp 6A được bảng sau:
|
Trái cây yêu thích |
Số học sinh chọn |
|
Cam |
8 |
|
Xoài |
10 |
|
Táo |
8 |
|
Ổi |
6 |
|
Quýt |
5 |
a) Loại trái cây nào có nhiều bạn yêu thích nhất?
b) Tính xác suất thực nghiệm của sự kiện một bạn học sinh được chọn ra một cách ngẫu nhiên loại trái cây yêu thích nhất là táo?
Bài 5. Cho đoạn thẳng MN = 6 cm, điểm P là trung điểm của đoạn thẳng MN, Q là trung điểm của đoạn thẳng MP. Tính độ dài đoạn thẳng MP, MQ.
Bài 6. Tìm số nguyên x, y biết \(\frac{3}{x} + \frac{y}{3} = \frac{5}{6}\).
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 7
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 7)
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
b) \(8\frac{2}{7} – \left( {3\frac{4}{9} + 4\frac{2}{7}} \right)\);
c) \(\frac{5}{{13}} + \frac{{ – 5}}{7} + \frac{{ – 20}}{{41}} + \frac{8}{{13}} + \frac{{ – 21}}{{41}}\)
d) \(1\frac{{13}}{{15}}.0,75 – \left( {\frac{8}{{15}} + 25\% } \right)\)
Bài 2. Tìm x biết:
a) \(\frac{3}{5}x – \frac{1}{2} = \frac{1}{7}\)
b) \(\left( {4,5 – 2x} \right).\frac{{11}}{7} = \frac{{11}}{{14}}\)
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
d) \(\frac{3}{4} – \left( {4\frac{1}{2} + 3x} \right) = – 1\)
Bài 3. Bạn An làm một số bài toán trong ba ngày, ngày đầu bạn làm được \(\frac{2}{3}\) tổng số bài, ngày thứ hai bạn làm được \(20\% \) tổng số bài, ngày thứ ba bạn làm nốt \(2\) bài. Hỏi trong ba ngày bạn An làm được bao nhiêu bài toán?
Bài 4. Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Trong 100 lần gieo xúc xắc thì mặt nào xuất hiện nhiều nhất? Mặt nào xuất hiện ít nhất?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn?
Bài 5.
1. Hình nào trong các hình sau có trục đối xứng đồng thời có tâm đối xứng?

2.
a) Vẽ góc xOy có số đo bằng 55°. Góc xOy là góc nhọn, góc vuông hay góc tù?
b) Trên Ox lấy hai điểm A, B sao cho OA = 2 cm, OB = 6 cm. Gọi \(M\) là trung điểm của đoạn thẳng AB. Tính AM.
Bài 6. Tìm số tự nhiên n để phân số \(B = \frac{{10n – 3}}{{4n – 10}}\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất.
Đáp án Đề số 7
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
b) \(8\frac{2}{7} – \left( {3\frac{4}{9} + 4\frac{2}{7}} \right)\);
c) \(\frac{5}{{13}} + \frac{{ – 5}}{7} + \frac{{ – 20}}{{41}} + \frac{8}{{13}} + \frac{{ – 21}}{{41}}\)
d) \(1\frac{{13}}{{15}}.0,75 – \left( {\frac{8}{{15}} + 25\% } \right)\)
Hướng dẫn giải:
a) (34,72 + 32,28) : 5 – (57,25 – 36,05) : 2;
= 67 : 5 + 21,2 : 2
= 13,4 – 10,6
= 2,8
b) \(8\frac{2}{7} – \left( {3\frac{4}{9} + 4\frac{2}{7}} \right)\);
\( = 8\frac{2}{7} – 3\frac{4}{9} – 4\frac{2}{7}\)
\( = \left( {8\frac{2}{7} – 4\frac{2}{7}} \right) – 3\frac{4}{9}\)
\( = \left[ {\left( {8 + \frac{2}{7}} \right) – \left( {4 + \frac{2}{7}} \right)} \right] – \left( {3 + \frac{4}{9}} \right)\)
\( = \left[ {\left( {8 – 4} \right) + \left( {\frac{2}{7} – \frac{2}{7}} \right)} \right] – \left( {3 + \frac{4}{9}} \right)\)
\( = 4 – 3 – \frac{4}{9}\)
\( = 1 – \frac{4}{9}\)
\( = \frac{9}{9} – \frac{4}{9}\)
\( = \frac{5}{9}\)
c) \(\frac{5}{{13}} + \frac{{ – 5}}{7} + \frac{{ – 20}}{{41}} + \frac{8}{{13}} + \frac{{ – 21}}{{41}}\)
\( = \left( {\frac{5}{{13}} + \frac{8}{{13}}} \right) + \left( {\frac{{ – 20}}{{41}} + \frac{{ – 21}}{{41}}} \right) + \frac{{ – 5}}{7}\)
\( = \frac{{13}}{{13}} + \frac{{ – 41}}{{41}} + \frac{{ – 5}}{7}\)
\( = 1 + \left( { – 1} \right) + \frac{{ – 5}}{7}\)
\( = 0 + \frac{{ – 5}}{7}\)
\( = \frac{{ – 5}}{7}\).
d) \(1\frac{{13}}{{15}}.0,75 – \left( {\frac{8}{{15}} + 25\% } \right)\)
\( = \frac{{28}}{{15}}.\frac{{75}}{{100}} – \left( {\frac{8}{{15}} + \frac{{25}}{{100}}} \right)\)
\[ = \frac{{4.7}}{{3.5}}.\frac{{3.25}}{{4.25}} – \left( {\frac{8}{{15}} + \frac{1}{4}} \right)\]
\( = \frac{7}{5} – \frac{8}{{15}} – \frac{1}{4}\)
\( = \frac{{84}}{{60}} – \frac{{32}}{{60}} – \frac{{15}}{{60}}\)
\( = \frac{{37}}{{60}}\)
Bài 2. Tìm x biết:
a) \(\frac{3}{5}x – \frac{1}{2} = \frac{1}{7}\)
b) \(\left( {4,5 – 2x} \right).\frac{{11}}{7} = \frac{{11}}{{14}}\)
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
d) \(\frac{3}{4} – \left( {4\frac{1}{2} + 3x} \right) = – 1\)
Hướng dẫn giải:
a) \(\frac{3}{5}x – \frac{1}{2} = \frac{1}{7}\)
\(\frac{3}{5}x = \frac{1}{7} + \frac{1}{2}\)
\(\frac{3}{5}x = \frac{2}{{14}} + \frac{7}{{14}}\)
\(\frac{3}{5}x = \frac{9}{{14}}\)
\(x = \frac{9}{{14}}:\frac{3}{5}\)
\(x = \frac{9}{{14}}.\frac{5}{3}\)
\(x = \frac{{15}}{{14}}\)
Vậy \(x = \frac{{15}}{{14}}\).
b) \(\left( {4,5 – 2x} \right).\frac{{11}}{7} = \frac{{11}}{{14}}\)
\[\frac{9}{2} – 2x = \frac{{11}}{{14}}:\frac{{11}}{7}\]
\(\frac{9}{2} – 2x = \frac{{11}}{{14}}.\frac{7}{{11}}\)
\(\frac{9}{2} – 2x = \frac{1}{2}\)
\(2x = \frac{9}{2} – \frac{1}{2}\)
\(2x = \frac{8}{2}\)
2x = 4
x = 2.
Vậy x = 2.
c) \[80\% + \frac{7}{6}:x = \frac{1}{6}\]
\(\frac{{80}}{{100}} + \frac{7}{6} = \frac{1}{6}\)
\[\frac{4}{5} + \frac{7}{6}:x = \frac{1}{6}\]
\[\frac{7}{6}:x = \frac{1}{6} – \frac{4}{5}\]
\[\frac{7}{6}:x = \frac{5}{{30}} – \frac{{24}}{{30}}\]
\[\frac{7}{6}:x = \frac{{ – 19}}{{30}}\]
\[x = \frac{7}{6}:\frac{{ – 19}}{{30}}\]
\(x = \frac{7}{6}.\frac{{30}}{{ – 19}}\)
\[x = \frac{{ – 35}}{{19}}\]
Vậy \[x = \frac{{ – 35}}{{19}}\].
d) \(\frac{3}{4} – \left( {4\frac{1}{2} + 3x} \right) = – 1\)
\(4\frac{1}{2} + 3x = \frac{3}{4} – \left( { – 1} \right)\)
\(\frac{9}{2} + 3x = \frac{3}{4} + 1\)
\(\frac{9}{2} + 3x = \frac{3}{4} + \frac{4}{4}\)
\(\frac{9}{2} + 3x = \frac{7}{4}\)
\(3x = \frac{9}{2} – \frac{7}{4}\)
\(3x = \frac{{18}}{4} – \frac{7}{4}\)
\(3x = \frac{{11}}{4}\)
\(x = \frac{{11}}{4}:3\)
\(x = \frac{{11}}{4}.\frac{1}{3}\)
\(x = \frac{{11}}{{12}}\)
Vậy \(x = \frac{{11}}{{12}}\).\(\)
Bài 3. Bạn An làm một số bài toán trong ba ngày, ngày đầu bạn làm được \(\frac{2}{3}\) tổng số bài, ngày thứ hai bạn làm được \(20\% \) tổng số bài, ngày thứ ba bạn làm nốt \(2\) bài. Hỏi trong ba ngày bạn An làm được bao nhiêu bài toán?
Hướng dẫn giải:
Ngày thứ nhất bạn An làm được \(\frac{2}{3}\) tổng số bài.
Ngày thứ hai bạn An làm được \(20\% \) tổng số bài, hay số bài làm được là \(\frac{{20}}{{100}} = \frac{1}{5}\) tổng số bài.
Vậy sau ngày thứ nhất và ngày thứ hai An làm được: \(\frac{2}{3} + \frac{1}{5} = \frac{{13}}{{15}}\) tổng số bài.
Vậy ngày thứ ba còn \(1 – \frac{{13}}{{15}} = \frac{2}{{15}}\) tổng số bài.
Ngày thứ ba bạn An làm nốt \(2\) bài nên ta có số bài làm trong ba ngày là:
\(2:\frac{2}{{15}} = 15\) bài.
Vậy tổng số bài bạn An làm là 15 bài.
Bài 4. Gieo con xúc xắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Trong 100 lần gieo xúc xắc thì mặt nào xuất hiện nhiều nhất? Mặt nào xuất hiện ít nhất?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn?
Hướng dẫn giải:
a) Trong 100 lần gieo xúc xắc thì mặt 6 chấm xuất hiện nhiều nhất và mặt 4 chấm xuất hiện ít nhất.
b) Các mặt có số chẵn chấm của con xúc xắc là mặt 2 chấm, 4 chấm, 6 chấm.
Tổng số lần xuất hiện mặt chấm chẵn là: 18 + 14 + 20 = 52 (lần).
Xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn là: \(\frac{{52}}{{100}} = 0,52.\)
Vậy xác suất của thực nghiệm của các sự kiện gieo được mặt có chấm chẵn là: 0,52.
Bài 5.
1. Hình nào trong các hình sau có trục đối xứng đồng thời có tâm đối xứng?

2.
a) Vẽ góc xOy có số đo bằng 55°. Góc xOy là góc nhọn, góc vuông hay góc tù?
b) Trên Ox lấy hai điểm A, B sao cho OA = 2 cm, OB = 6 cm. Gọi \(M\) là trung điểm của đoạn thẳng AB. Tính AM.
Hướng dẫn giải
1. Trong các hình trên thì Hình 1 là hình vừa có trục đối xứng vừa có tâm đối xứng.
2.
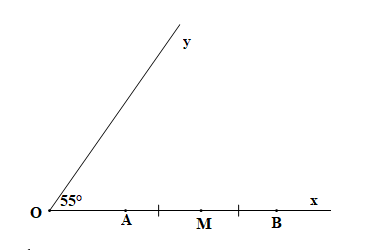
a) Góc xOy có số đo bằng 55° mà 55° < 90°
Do đó góc xOy là góc nhọn.
b) Trên \[{\rm{Ox}}\] lấy hai điểm A, B: OA = 2 cm, OB = 6 cm (OA < OB) nên điểm A nằm giữa hai điểm O và B.
Do đó OA + AB = OB.
Suy ra AB = OB – OA
Hay AB = 6 – 2 = 4 cm.
Vì M là trung điểm của đoạn thẳng OB nên \(AM = MB = \frac{{AB}}{2} = \frac{4}{2} = 2\) cm.
Bài 6. Tìm số tự nhiên n để phân số \(B = \frac{{10n – 3}}{{4n – 10}}\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất.
Hướng dẫn giải:
Ta có: \[B = \frac{{10n – 3}}{{4n – 10}} = \frac{{2,5\left( {4n – 10} \right) + 22}}{{4n – 10}}\]
\[ = \frac{{2,5\left( {4n – 10} \right)}}{{4n – 10}} + \frac{{22}}{{4n – 10}} = 2,5 + \frac{{22}}{{4n – 10}}\]
Vì n là số tự nhiên nên \[B = 2,5 + \frac{{22}}{{4n – 10}}\] đạt giá trị lớn nhất khi \[\frac{{22}}{{4n – 10}}\] đạt đạt giá trị lớn nhất.
Mà \[\frac{{22}}{{4n – 10}}\] đạt đạt giá trị lớn nhất khi 4n – 10 là số nguyên dương nhỏ nhất.
+) Nếu 4n – 10 = 1 thì 4n = 11 hay \(n = \frac{{11}}{4}\) (loại)
+) Nếu 4n – 10 = 2 thì 4n = 12 hay n = 3 (chọn)
Khi đó \(B = 2,5 + \frac{{22}}{2} = 13,5\)
Vậy B đạt giá trị lớn nhất là 13,5 khi n = 3.
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 8
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 8)
Câu 1. Các cặp phân số bằng nhau là:
A. \(\frac{{ – 6}}{7}\) và \(\frac{{ – 7}}{6}\);
B. \(\frac{{ – 3}}{5}\) và \(\frac{9}{{45}}\);
C. \(\frac{2}{3}\) và \(\frac{{ – 12}}{{18}}\);
D. \(\frac{{ – 1}}{4}\) và \(\frac{{ – 11}}{{44}}\).
Câu 2. Phân số nào là phân số thập phân:
A. \(\frac{7}{{100}};\)
B. \(\frac{{100}}{7};\)
C. \[\frac{{ – 15}}{{10,5}};\]
D. \(\frac{3}{2}.\)
Câu 3. Phân số nhỏ nhất trong các phân số \(\frac{3}{{ – 8}};\frac{{ – 5}}{8};\frac{{ – 1}}{8};\frac{7}{{ – 8}}\) là:
A. \(\frac{3}{{ – 8}};\)
B. \(\frac{{ – 5}}{8};\)
C. \(\frac{{ – 1}}{8};\)
D. \(\frac{7}{{ – 8}}.\)
Câu 4. Cho \(\frac{{12}}{x} = \frac{{ – 2}}{3}\). Số x thích hợp là:
A. 18;
B. – 18;
C. 4;
D. – 4.
Câu 5. Giá trị của x trong phép tính 3.x + 25%.x = 0,75 là:
A. \(\frac{3}{{13}};\)
B. \(\frac{7}{{13}};\)
C. 3;
D. 7.\(\)
Câu 6. Lớp 6A có 36 học sinh. Trong đó có 25% số học sinh đạt danh hiệu học sinh giỏi. Số học sinh giỏi là:
A. 9;
B. 4;
C. 6;
D. 11.
Câu 7. Tại một cửa hàng, một chú gấu bông có giá 300 000 đồng. Nhân ngày Quốc tế Thiếu nhi, cửa hàng thực hiện giảm giá 45% các mặt hàng. Hỏi giá bán của chú gấu bông sau khi đã giảm là bao nhiêu?
A. 135 000 đồng;
B. 235 000 đồng;
C. 155 000 đồng;
D. 165 000 đồng.
Câu 8. Viết hỗn số \(2\frac{8}{7}\) dưới dạng số thập phân (làm tròn đến chữ số thập phân thứ nhất).
A. 3,1;
B. 3,14;
C. 3,15;
D. 3,2.
Câu 9. Diện tích đất trồng trọt của một xã là khoảng 81,5 ha. Vụ hè thu năm nay, xã này dự định dùng \(\frac{5}{7}\) diện tích này để trồng lúa. Tính diện tích trồng lúa vụ thu hè của xã (làm tròn kết quả chữ số thập phân thứ ba):
A. 58,214 ha;
B. 58,210 ha;
C. 58,215 ha;
D. 58,220 ha.
Câu 10: Sau một thời gian gửi tiết kiệm, người gửi đi rút tiền và nhận được 320 000 đồng tiền lãi. Biết rằng số lãi bằng \(\frac{1}{{25}}\) số tiền gửi tiết kiệm. Tổng số tiền người đó nhận được là:
A. 8 000 000 đồng;
B. 8 320 000 đồng;
C. 7 680 000 đồng;
D. 2 400 000 đồng.
Câu 11. Trong chương trình khuyến mại giảm giá 20%, hộp sữa bột có giá là 840 000 đồng. Như vậy khi mua một hộp sữa với giá niêm yết người mua cần phải trả số tiền là:
A. 168 000 đồng;
B. 672 000 đồng;
C. 4 200 000 đồng;\(\quad \)
D. 1 050 000 đồng.
Câu 12. Tỉ số phần trăm của 0,3 tạ và 50 kg là:
A. 60%;
B. 600%;
C. 6%;
D. 0,6%.
Câu 13. Kết quả của phép tính (–14,3) : (–2,5) là:
A. –57,2;
B. –5,72;
C. 5,72 .
D. 57,2 .
Câu 14. Giá trị của x thoả mãn \(2\frac{2}{3}:x = 2\frac{1}{{12}}:( – 0,06)\) là :
A. 0,0786;
B. 0,786;
C. –0,768;
D. –0,0768.
Câu 15. Kết quả của phép tính (–4,44 + 60 – 5,56) : (1,2 – 0,8) là:
A. –152;
B. –125;
C. 152;
D. 125.
Câu 16. Tính hợp lí biểu thức \(\frac{2}{{11}} – \frac{3}{8} + \frac{4}{{11}} – \frac{6}{{11}} – \frac{5}{8}\) được kết quả là:
A. \(\frac{2}{{11}}\);
B. \(\frac{{ – 9}}{{11}}\);
C. – 1;
D. 1.
Câu 17. Kết quả của phép tính \(\frac{{ – 5}}{7} \cdot \frac{2}{{11}} + \frac{{ – 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\) là:
A. 1;
B. 2;
C. 0;
D. 4.
Câu 18. So sánh \(a = \frac{{2525}}{{2626}}\) với \(b = \frac{{20212021}}{{20222022}}\)
A. a > b;
B. a ≥ b;
C. a < b;
D. a = b.
Câu 19. Biết tỉ số phần trăm của nước trong dưa chuột là 92,8%. Lượng nước trong 10 kg dưa chuột là:
A. 12,88 kg;
B. 9,28 kg;
C. 10,76 kg;
D. 3,8 kg.
Câu 20. Trong các hình sau đây, hình nào không có trục đối xứng (mỗi hình là một từ)?

A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Câu 21. Trong các hình sau, điểm O là tâm đối xứng của hình nào?
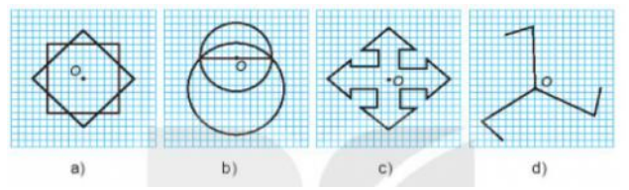
A. Hình a, b, c;
B. Hình a, b;
C. Hình c, d;
D. Hình a, c.
Câu 22. Trong các phát biểu sau, phát biểu nào sai?
A. Chữ cái in hoa I có một tâm đối xứng;
B. Tam giác đều có một tâm đối xứng;
C. Đường tròn có tâm là tâm đối xứng;
D. Hình bình hành nhận giao điểm của hai đường chéo làm tâm đối xứng.
Câu 23. Cho hình vẽ dưới đây. Có bao nhiêu cặp đường thẳng song song?
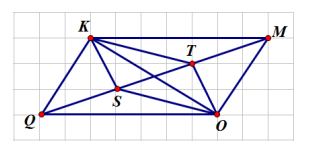
A. 3;
B. 4;
C. 5;
D. 6.
Câu 24. Hình vẽ dưới đây có bao nhiêu đoạn thẳng?
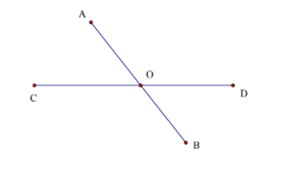
A. 3;
B. 4;
C. 5;
D. 6.
Câu 25. Cho AB = 2 cm và D là trung điểm. Vẽ điểm E sao cho B là trung điểm của đoạn thẳng ED. Khi đó độ dài của đoạn thẳng ED là:
A. 1 cm;
B. 2 cm;
C. 3 cm;
D. 4 cm.
Câu 26. Cho tam giác BDN, trên cạnh BN lấy điểm M khác hai điểm B và N. Các góc nhận tia DB làm cạnh là:
A. \(\widehat {BMD};\widehat {BDN}\);
B. \(\widehat {BDM};\widehat {BDN}\);
C. \(\widehat {DBM};\widehat {BDN}\);
D. \(\widehat {BDM};\widehat {DBN}\).
Câu 27. Biết khi hai kim đồng hồ chỉ vào hai số liên tiếp nhau thì góc giữa hai kim đồng hồ là 30°. Góc tạo bởi kim phút và kim giờ tại thời điểm 7 giờ là:
A. 30°;
B. 70°;
C. 150°;
D. 180°.
Câu 28. Trong các hình sau, hình nào không có trục đối xứng?

A. Hình Quốc huy Việt Nam;
B. Hình Huy hiệu Đội TNTP HCM;
C. Hình Huy hiệu Đoàn TNCS HCM;
D. Hình lá cờ Tổ quốc Việt Nam.
Câu 29. Đường thẳng a chứa những điểm nào?
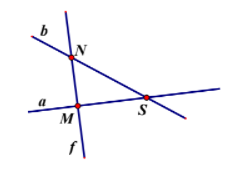
A. M và N;
B. M và S;
C. N và S;
D. M, N và S.
Câu 30. Khẳng định đúng là
A. Góc có số đo 120° là góc vuông;
B. Góc có số đo 80° là góc tù;
C. Góc có số đo 100° là góc nhọn;
D. Góc có số đo 140° là góc tù.
Câu 31. Có bao nhiêu biển báo giao thông dưới đây có tâm đối xứng?
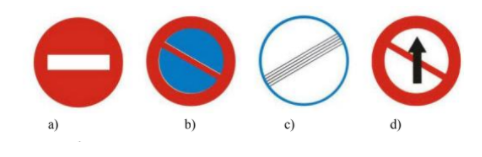
A. 1 biển báo;
B. 2 biển báo;
C. 3 biển báo;
D. 4 biển báo.
Câu 32. Chọn phát biểu đúng trong các phát biểu sau:
A. Một sự kiện có thể xảy ra hoặc không thể xảy ra tùy thuộc vào kết quả của phép thử nghiệm đó.
B. Một sự kiện có thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
C. Một sự kiện đồng thời có thể xảy ra hoặc không thể xảy ra trong phép thử nghiệm đó.
D. Một sự kiện có thể xảy ra hoặc không thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
Câu 33. Cuối tuần, Tuấn được bố mẹ cho phép đến nhà Khang chơi nhưng con đường Tuấn thường đi đang sửa chữa nên Tuấn phải đi đường khác. Giữa đường có 4 ngã rẽ, nhưng chỉ có một ngã dẫn đến nhà Khang, Tuấn không nhớ cần rẽ ngã nào. Có mấy kết quả có thể khi Tuấn chọn ngã rẽ? Liệt kê.
A. 2 kết quả: đến được nhà Khang, không đến được nhà Khang.
B. 3 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang.
C. 4 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang, bị lạc đường.
D. Tất cả đều sai.
Câu 34. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm 8, điểm 9 và điểm 10 là:
A. 1;
B. 6;
C. 7;
D. 12.
Câu 35. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm dưới 5 là:
A. 1;
B. 2;
C. 3;
D. 11.
Câu 36. Gieo một con xúc xắc, sự kiện “số chấm xuất hiện là số nguyên tố” xảy ra khi số chấm trên con xúc xắc là bao nhiêu? Chọn câu sai:
A. 2;
B. 2; 5;
C. 1; 4; 6;
D. 2; 3; 5.
Câu 37. Để nói về khả năng xảy ra của một sự kiện, ta dùng một con số có giá trị từ:
A. 0 đến 1;
B. 1 đến 10;
C. 0 đến 10;
D. 0 đến 100.
Câu 38. Bạn Nam gieo một con xúc xắc 20 lần liên tiếp thì thấy mặt 6 chấm xuất hiện 3 lần. Xác suất thực nghiệm xuất hiện mặt 6 chấm là:
A. \(\frac{3}{{10}}\);
B. \(\frac{3}{{20}}\);
C. \(\frac{6}{{20}}\);
D. \(\frac{6}{{23}}\).
Câu 39. Một xạ thủ bắn 20 mũi tên vào một tấm bia. Điểm số ở các lần bắn được cho bởi bảng sau:
|
7 |
8 |
9 |
9 |
8 |
10 |
10 |
9 |
8 |
10 |
|
8 |
8 |
9 |
10 |
10 |
7 |
6 |
6 |
9 |
9 |
Xác suất thực nghiệm để xạ thủ bắn được 10 điểm là:
A. \(\frac{1}{4}\);
B. \(\frac{1}{2}\);
C. \(\frac{{10}}{{20}}\);
D. \(\frac{7}{{20}}\).
Câu 40. Gieo một con xúc xắc 6 mặt 80 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
12 |
15 |
14 |
18 |
10 |
11 |
Xác suất thực nghiệm của sự kiện gieo được mặt chấm là số lẻ là:
A. \(\frac{{11}}{{80}}\);
B. \(\frac{9}{{40}}\);
C. \(\frac{{11}}{{20}}\);
D. \(\frac{9}{{20}}\).
Đáp án Đề số 8
Câu 1. Các cặp phân số bằng nhau là:
A. \(\frac{{ – 6}}{7}\) và \(\frac{{ – 7}}{6}\);
B. \(\frac{{ – 3}}{5}\) và \(\frac{9}{{45}}\);
C. \(\frac{2}{3}\) và \(\frac{{ – 12}}{{18}}\);
D. \(\frac{{ – 1}}{4}\) và \(\frac{{ – 11}}{{44}}\).
Hướng dẫn giải:
Đáp án đúng là: D
Ta có \(\frac{{ – 11}}{{44}} = \frac{{\left( { – 11} \right):11}}{{44:11}} = \frac{{ – 1}}{4}\).
Câu 2. Phân số nào là phân số thập phân:
A. \(\frac{7}{{100}};\)
B. \(\frac{{100}}{7};\)
C. \[\frac{{ – 15}}{{10,5}};\]
D. \(\frac{3}{2}.\)
Hướng dẫn giải:
Đáp án đúng là: A
Phân số thập phân là \(\frac{7}{{100}}.\)
Câu 3. Phân số nhỏ nhất trong các phân số \(\frac{3}{{ – 8}};\frac{{ – 5}}{8};\frac{{ – 1}}{8};\frac{7}{{ – 8}}\) là:
A. \(\frac{3}{{ – 8}};\)
B. \(\frac{{ – 5}}{8};\)
C. \(\frac{{ – 1}}{8};\)
D. \(\frac{7}{{ – 8}}.\)
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(\frac{3}{{ – 8}} = \frac{{ – 3}}{8};\frac{7}{{ – 8}} = \frac{{ – 7}}{8}\).
Do đó \(\frac{{ – 7}}{8} < \frac{{ – 5}}{8} < \frac{{ – 3}}{8} < \frac{{ – 1}}{8}.\)
Vậy phân số nhỏ nhất là \(\frac{7}{{ – 8}}.\)
Câu 4. Cho \(\frac{{12}}{x} = \frac{{ – 2}}{3}\). Số x thích hợp là:
A. 18;
B. – 18;
C. 4;
D. – 4.
Hướng dẫn giải:
Đáp án đúng là: B
Có \(\frac{{12}}{x} = \frac{{ – 2}}{3}\) nên (– 2).x = 12.3
Suy ra \(x = \frac{{12.3}}{{ – 2}}\)
x = – 18.
Vậy x = – 18.
Câu 5. Giá trị của x trong phép tính 3.x + 25%.x = 0,75 là:
A. \(\frac{3}{{13}};\)
B. \(\frac{7}{{13}};\)
C. 3;
D. 7.\(\)
Hướng dẫn giải:
Đáp án đúng là: A
Vì: 3.x + 25%.x = 0,75
\(3x + \frac{{25}}{{100}}x = \frac{{75}}{{100}}\)
\(x.\left( {3 + \frac{{25}}{{100}}} \right) = \frac{3}{4}\)
\(x.\left( {3 + \frac{1}{4}} \right) = \frac{3}{4}\)
\(x\left( {\frac{{12}}{4} + \frac{1}{4}} \right) = \frac{3}{4}\)
\(x.\frac{{13}}{4} = \frac{3}{4}\)
\(x = \frac{3}{4}:\frac{{13}}{4}\)
\(x = \frac{3}{4}.\frac{4}{{13}}\)
\(x = \frac{3}{{13}}\)
Vậy \(x = \frac{3}{{13}}.\)
Câu 6. Lớp 6A có 36 học sinh. Trong đó có 25% số học sinh đạt danh hiệu học sinh giỏi. Số học sinh giỏi là:
A. 9;
B. 4;
C. 6;
D. 11.
Hướng dẫn giải:
Đáp án đúng là: A
Số học sinh giỏi của lớp 6A là: \(36.25\% = 36.\frac{1}{4} = 9\) (học sinh).
Câu 7. Tại một cửa hàng, một chú gấu bông có giá 300 000 đồng. Nhân ngày Quốc tế Thiếu nhi, cửa hàng thực hiện giảm giá 45% các mặt hàng. Hỏi giá bán của chú gấu bông sau khi đã giảm là bao nhiêu?
A. 135 000 đồng;
B. 235 000 đồng;
C. 155 000 đồng;
D. 165 000 đồng.
Hướng dẫn giải:
Đáp án đúng là: D
Số tiền được giảm khi mua chú gấu bông là: 300 000 . 45% = 135 000 (đồng).
Số tiền phải trả khi mua chú gấu bông là: 300 000 – 135 000 = 165 000 (đồng).
Câu 8. Viết hỗn số \(2\frac{8}{7}\) dưới dạng số thập phân (làm tròn đến chữ số thập phân thứ nhất).
A. 3,1;
B. 3,14;
C. 3,15;
D. 3,2.
Hướng dẫn giải:
Đáp án đúng là: A
Ta có \(2\frac{8}{7} = \frac{{2.7 + 8}}{7} = \frac{{22}}{7} = 3,1428…\)
Vì số 3,1428…có chữ số thập phân thứ hai là 4 < 5 nên khi làm tròn đến chữ số thập phân thứ nhất ta được 3,1.
Câu 9. Diện tích đất trồng trọt của một xã là khoảng 81,5 ha. Vụ hè thu năm nay, xã này dự định dùng \(\frac{5}{7}\) diện tích này để trồng lúa. Tính diện tích trồng lúa vụ thu hè của xã (làm tròn kết quả chữ số thập phân thứ ba):
A. 58,214 ha;
B. 58,210 ha;
C. 58,215 ha;
D. 58,220 ha.
Hướng dẫn giải:
Đáp án đúng là: A
Diện tích trồng lúa vụ thu hè của xã là: \(81,5 \cdot \frac{5}{7} = 58,2142\) (ha)
Làm tròn kết quả đến chữ số thập phân thứ ba ta được kết quả là 58,214 (ha).
Câu 10: Sau một thời gian gửi tiết kiệm, người gửi đi rút tiền và nhận được 320 000 đồng tiền lãi. Biết rằng số lãi bằng \(\frac{1}{{25}}\) số tiền gửi tiết kiệm. Tổng số tiền người đó nhận được là:
A. 8 000 000 đồng;
B. 8 320 000 đồng;
C. 7 680 000 đồng;
D. 2 400 000 đồng.
Hướng dẫn giải:
Đáp án đúng là: B
Vì số tiền lãi bằng \(\frac{1}{{25}}\) số tiền gửi tiết kiệm nên số tiền tiết kiệm là:
\(320\;000:\frac{1}{{25}} = 8\;000\;000\)(đồng)
Tổng số tiền người đó nhận được là:
8 000 000 + 320 000 = 8 320 000 (đồng)
Câu 11. Trong chương trình khuyến mại giảm giá 20%, hộp sữa bột có giá là 840 000 đồng. Như vậy khi mua một hộp sữa với giá niêm yết người mua cần phải trả số tiền là:
A. 168 000 đồng;
B. 672 000 đồng;
C. 4 200 000 đồng;\(\quad \)
D. 1 050 000 đồng.
Hướng dẫn giải:
Đáp án đúng là: D
Khi giảm 20% thì giá của hộp sữa là 840 000 đồng nên người mua đã phải trả 80% giá niêm yết của hộp sữa.
Vậy giá niêm yết của hộp sữa là: 840 000 : 80% = 1 050 000 (đồng).
Vậy giá niêm yết của hộp sữa là: 1 050 000 (đồng).
Câu 12. Tỉ số phần trăm của 0,3 tạ và 50 kg là:
A. 60%;
B. 600%;
C. 6%;
D. 0,6%.
Hướng dẫn giải:
Đáp án đúng là: A
Vì 0,3 tạ = 30 kg nên tỉ số phần trăm của 0,3 tạ và 50 kg là: \(\frac{{30}}{{50}}.100\% = 60\% \).
Vậy tỉ số phần trăm của 0,3 tạ và 50 kg là 60%.
Câu 13. Kết quả của phép tính (–14,3) : (–2,5) là:
A. –57,2;
B. –5,72;
C. 5,72 .
D. 57,2 .
Hướng dẫn giải:
Đáp án đúng là: C
(–14,3) : (–2,5) = 5,72.
Câu 14. Giá trị của x thoả mãn \(2\frac{2}{3}:x = 2\frac{1}{{12}}:( – 0,06)\) là :
A. 0,0786;
B. 0,786;
C. –0,768;
D. –0,0768.
Huớng dẫn giải:
Đáp án đúng là: D
\(2\frac{2}{3}:x = 2\frac{1}{{12}}:( – 0,06)\)
\(\frac{8}{3}:x = \frac{{25}}{{12}}:\frac{{ – 6}}{{100}}\)
\[\frac{8}{3}:x = \frac{{25}}{{12}}.\frac{{100}}{{ – 6}}\]
\[\frac{8}{3}:x = \frac{{25.4.25}}{{3.4.\left( { – 6} \right)}}\]
\(\frac{8}{3}:x = \frac{{625}}{{ – 18}}\)
\(x = \frac{8}{3}:\frac{{625}}{{ – 18}}\)
\(x = \frac{8}{3}.\frac{{ – 18}}{{625}}\)
\(x = \frac{8}{3}.\frac{{ – 3.6}}{{625}}\)
\(x = \frac{{ – 48}}{{625}}\)
x = –0,0768.
Vậy x = –0,0768.
Câu 15. Kết quả của phép tính (–4,44 + 60 – 5,56) : (1,2 – 0,8) là:
A. –152;
B. –125;
C. 152;
D. 125.
Hướng dẫn giải:
Đáp án đúng là: D
(–4,44 + 60 – 5,56) : (1,2 – 0,8)
= [60 + (– 4,44 – 5,56)] : 0,4
= [60 + (–10)] : 0,4
= 50 : 0,4
= 125.
Câu 16. Tính hợp lí biểu thức \(\frac{2}{{11}} – \frac{3}{8} + \frac{4}{{11}} – \frac{6}{{11}} – \frac{5}{8}\) được kết quả là:
A. \(\frac{2}{{11}}\);
B. \(\frac{{ – 9}}{{11}}\);
C. – 1;
D. 1.
Hướng dẫn giải:
Đáp án đúng là: C
Ta có: \(\frac{2}{{11}} – \frac{3}{8} + \frac{4}{{11}} – \frac{6}{{11}} – \frac{5}{8}\)
\( = \left( {\frac{2}{{11}} + \frac{4}{{11}} – \frac{6}{{11}}} \right) + \left( { – \frac{3}{8} – \frac{5}{8}} \right)\)
\( = \frac{0}{{11}} + \frac{{ – 8}}{8}\)
= – 1.
Câu 17. Kết quả của phép tính \(\frac{{ – 5}}{7} \cdot \frac{2}{{11}} + \frac{{ – 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\) là:
A. 1;
B. 2;
C. 0;
D. 4.
Hướng dẫn giải:
Đáp án đúng là: C
Ta thấy:
\(\frac{{ – 5}}{7} \cdot \frac{2}{{11}} + \frac{{ – 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7} = \frac{{ – 5}}{7}\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{5}{7} = \frac{{ – 5}}{7}.\frac{{11}}{{11}} + \frac{5}{7} = \frac{{ – 5}}{7} \cdot 1 + \frac{5}{7} = \frac{{ – 5}}{7} + \frac{5}{7} = 0\)
Câu 18. So sánh \(a = \frac{{2525}}{{2626}}\) với \(b = \frac{{20212021}}{{20222022}}\)
A. a > b;
B. a ≥ b;
C. a < b;
D. a = b.
Hướng dẫn giải:
Đáp án đúng là: C
+) Ta có: \(a = \frac{{2525}}{{2626}} = \frac{{25.101}}{{26.101}} = \frac{{25}}{{26}}\)
Suy ra \(1 – a = 1 – \frac{{25}}{{26}} = \frac{1}{{26}}\);
Ta có: \[b = \frac{{20212021}}{{20222022}} = \frac{{2021.10001}}{{2022.10001}} = \frac{{2021}}{{2022}}\]
Suy ra \[1 – b = 1 – \frac{{2021}}{{2022}} = \frac{1}{{2022}}\]
Vì 26 < 2022 nên \(\frac{1}{{26}} > \frac{1}{{2022}}\) hay 1 – a > 1 – b
Do đó a < b.
Câu 19. Biết tỉ số phần trăm của nước trong dưa chuột là 92,8%. Lượng nước trong 10 kg dưa chuột là:
A. 12,88 kg;
B. 9,28 kg;
C. 10,76 kg;
D. 3,8 kg.
Hướng dẫn giải:
Đáp án đúng là: B
Ta có lượng nước có trong 10 kg dưa chuột là:
10. 92,8% = 9,28 kg.
Câu 20. Trong các hình sau đây, hình nào không có trục đối xứng (mỗi hình là một từ)?

A. Hình 1;
B. Hình 2;
C. Hình 3;
D. Hình 4.
Hướng dẫn giải:
Đáp án đúng là: D
Trừ hình 4 ra, các hình còn lại đều có trục đối xứng.
Câu 21. Trong các hình sau, điểm O là tâm đối xứng của hình nào?
A. Hình a, b, c;
B. Hình a, b;
C. Hình c, d;
D. Hình a, c.
Hướng dẫn giải:
Đáp án đúng là: A
Trong các hình trên, Hình a và c có tâm đối xứng là điểm O.
Câu 22. Trong các phát biểu sau, phát biểu nào sai?
A. Chữ cái in hoa I có một tâm đối xứng;
B. Tam giác đều có một tâm đối xứng;
C. Đường tròn có tâm là tâm đối xứng;
D. Hình bình hành nhận giao điểm của hai đường chéo làm tâm đối xứng.
Hướng dẫn giải:
Đáp án đúng là: B
Tam giác đều không có tâm đối xứng.
Câu 23. Cho hình vẽ dưới đây. Có bao nhiêu cặp đường thẳng song song?
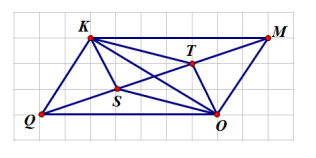
A. 3;
B. 4;
C. 5;
D. 6.
Hướng dẫn giải:
Đáp án đúng là: B
Dựa vào hình vẽ, ta thấy có các cặp đường thẳng song song và KM và QO, KQ và MO; KT và SO; KS và TO.
Vậy có tất cả 4 cặp đường thẳng song song.
Câu 24. Hình vẽ dưới đây có bao nhiêu đoạn thẳng?
A. 3;
B. 4;
C. 5;
D. 6.
Hướng dẫn giải:
Đáp án đúng là: D
Có 6 đoạn thẳng là OA; OB; OC; OD; AB; CD.
Câu 25. Cho AB = 2 cm và D là trung điểm. Vẽ điểm E sao cho B là trung điểm của đoạn thẳng ED. Khi đó độ dài của đoạn thẳng ED là:
A. 1 cm;
B. 2 cm;
C. 3 cm;
D. 4 cm.
Hướng dẫn giải:
Đáp án đúng là: B
Vì D là trung điểm của AB nên \(AD = DB = \frac{1}{2}AB = \frac{1}{2}.2 = 1\) cm.
B là trung điểm của ED nên \(EB = DB = \frac{1}{2}ED\)
Suy ra ED = 2.DB.
Do đó ED = 2.DB = 2.1 = 2 cm.
Câu 26. Cho tam giác BDN, trên cạnh BN lấy điểm M khác hai điểm B và N. Các góc nhận tia DB làm cạnh là:
A. \(\widehat {BMD};\widehat {BDN}\);
B. \(\widehat {BDM};\widehat {BDN}\);
C. \(\widehat {DBM};\widehat {BDN}\);
D. \(\widehat {BDM};\widehat {DBN}\).
Hướng dẫn giải:
Đáp án đúng là: B
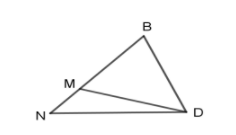
Các góc nhận tia DB làm cạnh là: \(\widehat {BDM};\widehat {BDN}\).
Câu 27. Biết khi hai kim đồng hồ chỉ vào hai số liên tiếp nhau thì góc giữa hai kim đồng hồ là 30°. Góc tạo bởi kim phút và kim giờ tại thời điểm 7 giờ là:
A. 30°;
B. 70°;
C. 150°;
D. 180°.
Hướng dẫn giải:
Đáp án đúng là: C
Tại thời điểm 7 giờ, góc giữa kim phút và kim giờ là (12 – 7).30° = 150°.
Câu 28. Trong các hình sau, hình nào không có trục đối xứng?

A. Hình Quốc huy Việt Nam;
B. Hình Huy hiệu Đội TNTP HCM;
C. Hình Huy hiệu Đoàn TNCS HCM;
D. Hình lá cờ Tổ quốc Việt Nam.
Hướng dẫn giải:
Đáp án đúng là: C
Hình Huy hiệu Đoàn TNCS HCM là hình không có trục đối xứng.
Câu 29. Đường thẳng a chứa những điểm nào?
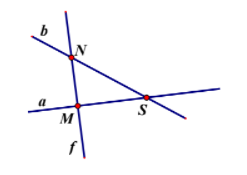
A. M và N;
B. M và S;
C. N và S;
D. M, N và S.
Hướng dẫn giải:
Đáp án đúng là: B
Đường thẳng a chứa các điểm M và S.
Câu 30. Khẳng định đúng là
A. Góc có số đo 120° là góc vuông;
B. Góc có số đo 80° là góc tù;
C. Góc có số đo 100° là góc nhọn;
D. Góc có số đo 140° là góc tù.
Hướng dẫn giải:
Đáp án đúng là: D
Góc có số đo 140° > 90° là góc tù.
Câu 31. Có bao nhiêu biển báo giao thông dưới đây có tâm đối xứng?
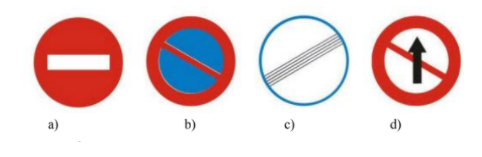
A. 1 biển báo;
B. 2 biển báo;
C. 3 biển báo;
D. 4 biển báo.
Hướng dẫn giải:
Đáp án đúng là: C
Hình d không có tâm đối xứng. Do đó có 3 biển báo có tâm đối xứng.
Câu 32. Chọn phát biểu đúng trong các phát biểu sau:
A. Một sự kiện có thể xảy ra hoặc không thể xảy ra tùy thuộc vào kết quả của phép thử nghiệm đó.
B. Một sự kiện có thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
C. Một sự kiện đồng thời có thể xảy ra hoặc không thể xảy ra trong phép thử nghiệm đó.
D. Một sự kiện có thể xảy ra hoặc không thể xảy ra không tùy thuộc vào kết quả của phép thử nghiệm đó.
Hướng dẫn giải:
Đáp án đúng là: A
Khi thực hiện phép thử nghiệm thì một sự kiện có thể xảy ra hoặc không thể xảy ra tùy thuộc vào kết quả của phép thử nghiệm đó.
Câu 33. Cuối tuần, Tuấn được bố mẹ cho phép đến nhà Khang chơi nhưng con đường Tuấn thường đi đang sửa chữa nên Tuấn phải đi đường khác. Giữa đường có 4 ngã rẽ, nhưng chỉ có một ngã dẫn đến nhà Khang, Tuấn không nhớ cần rẽ ngã nào. Có mấy kết quả có thể khi Tuấn chọn ngã rẽ? Liệt kê.
A. 2 kết quả: đến được nhà Khang, không đến được nhà Khang.
B. 3 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang.
C. 4 kết quả: đến được nhà Khang, không đến được nhà Khang, đi xa hơn để đến nhà Khang, bị lạc đường.
D. Tất cả đều sai.
Hướng dẫn giải:
Đáp án đúng là: A
Vì trong 4 ngã rẽ, chỉ có 1 ngã rẽ dẫn đến nhà Khang, 3 ngã rẽ còn lại đều không đến được nhà Khang nên chỉ có 2 kết quả có thể là: đến được nhà Khang và không đến được nhà Khang.
Câu 34. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm 8, điểm 9 và điểm 10 là:
A. 1;
B. 6;
C. 7;
D. 12.
Hướng dẫn giải:
Đáp án đúng là: D
Số học sinh đạt điểm 8, điểm 9 và điểm 10 là: 5 + 6 +1 = 12 (học sinh).
Câu 35. Kết quả kiểm tra môn Toán của học sinh lớp 6A được cho bởi bảng sau:
|
Điểm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số học sinh |
0 |
0 |
0 |
2 |
1 |
8 |
8 |
9 |
5 |
6 |
1 |
Số học sinh đạt điểm dưới 5 là:
A. 1;
B. 2;
C. 3;
D. 11.
Hướng dẫn giải:
Đáp án đúng là: C
Số học sinh đạt điểm dưới 5 là: 0 + 0 + 0 + 2 + 1 = 3 (học sinh).
Câu 36. Gieo một con xúc xắc, sự kiện “số chấm xuất hiện là số nguyên tố” xảy ra khi số chấm trên con xúc xắc là bao nhiêu? Chọn câu sai:
A. 2;
B. 2; 5;
C. 1; 4; 6;
D. 2; 3; 5.
Hướng dẫn giải:
Đáp án đúng là: D
Sự kiện “số chấm xuất hiện là số nguyên tố” xảy ra tức là xuất hiện một trong các số 2; 3; 5.
Câu 37. Để nói về khả năng xảy ra của một sự kiện, ta dùng một con số có giá trị từ:
A. 0 đến 1;
B. 1 đến 10;
C. 0 đến 10;
D. 0 đến 100.
Hướng dẫn giải:
Đáp án đúng là: A
Khi thực hiện phép thực nghiệm, một sự kiện có thể xảy ra hoặc không xảy ra. Khả năng xảy ra của một sự kiện được thể hiện bằng một con số từ 0 đến 1.
Câu 38. Bạn Nam gieo một con xúc xắc 20 lần liên tiếp thì thấy mặt 6 chấm xuất hiện 3 lần. Xác suất thực nghiệm xuất hiện mặt 6 chấm là:
A. \(\frac{3}{{10}}\);
B. \(\frac{3}{{20}}\);
C. \(\frac{6}{{20}}\);
D. \(\frac{6}{{23}}\).
Hướng dẫn giải:
Đáp án đúng là: B
Tổng số lần thực hiện hoạt động gieo xúc xắc là 20, số lần mặt 6 chấm xuất hiện là 3 lần.
Xác suất thực nghiệm xuất hiện mặt 6 chấm là: \(\frac{3}{{20}}\).
Câu 39. Một xạ thủ bắn 20 mũi tên vào một tấm bia. Điểm số ở các lần bắn được cho bởi bảng sau:
|
7 |
8 |
9 |
9 |
8 |
10 |
10 |
9 |
8 |
10 |
|
8 |
8 |
9 |
10 |
10 |
7 |
6 |
6 |
9 |
9 |
Xác suất thực nghiệm để xạ thủ bắn được 10 điểm là:
A. \(\frac{1}{4}\);
B. \(\frac{1}{2}\);
C. \(\frac{{10}}{{20}}\);
D. \(\frac{7}{{20}}\).
Hướng dẫn giải:
Đáp án đúng là: A
Tổng số lần xạ thủ bắn mũi tên vào bia là 20, số lần xạ thủ bắn được 10 điểm là 5 lần.
Xác suất thực nghiệm để xạ thủ bắn được 10 điểm là: \(\frac{5}{{20}} = \frac{1}{4}\).
Câu 40. Gieo một con xúc xắc 6 mặt 80 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
12 |
15 |
14 |
18 |
10 |
11 |
Xác suất thực nghiệm của sự kiện gieo được mặt chấm là số lẻ là:
A. \(\frac{{11}}{{80}}\);
B. \(\frac{9}{{40}}\);
C. \(\frac{{11}}{{20}}\);
D. \(\frac{9}{{20}}\).
Hướng dẫn giải:
Đáp án đúng là: D
Các mặt có số chấm là số lẻ của con xúc xắc là mặt 1 chấm, mặt 3 chấm và mặt 5 chấm.
Tổng số lần thực hiện gieo con xúc xắc 6 mặt là:
12 + 15 + 14 + 18 + 10 + 11 = 80 (lần)
Số lần xuất hiện mặt 1 chấm, 3 chấm, 5 chấm là: 12 +14 +10 = 36 (lần).
Xác suất thực nghiệm của sự kiện gieo được các mặt chấm là số lẻ là: \(\frac{{36}}{{80}} = \frac{9}{{20}}\)
Vậy xác suất thực nghiệm của sự kiện gieo được các mặt chấm là số lẻ là: \(\frac{{36}}{{80}} = \frac{9}{{20}}\)
Bộ 20 Đề thi Toán lớp 6 Học kì 2 năm 2024 – Chân trời sáng tạo – Đề 9
Phòng Giáo dục và Đào tạo …
Đề thi Học kì 2 – Chân trời sáng tạo
Năm học 2023 – 2024
Bài thi môn: Toán lớp 6
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 9)
Câu 1. Số đối của phân số \(\frac{4}{5}\) là:
A. \(\frac{{ – 4}}{5};\)
B. \(\frac{4}{5};\)
C. \(\frac{5}{4};\)
D. \(\frac{{ – 5}}{4}.\)
Câu 2. Biết \[\frac{1}{3}\] quả dưa hấu nặng \(0,8{\rm{ kg}}\).Quả dưa hấu đó nặng là:
A. 3 kg;
B. 3,2 kg;
C. 2,4 kg;
D. 4,2 kg.
Câu 3. Tổng của hai phân số \(\frac{7}{{15}}\) và \(\frac{{ – 2}}{5}\) bằng:
A. \(\frac{5}{{10}}\) ;
B. \(\frac{5}{{20}}\);
C. \(\frac{1}{{15}}\);
D. \[\frac{{ – 1}}{{15}}.\]
Câu 4. Một xạ thủ bắn 20 mũi tên vào một tấm bia thì được 18 lần trúng. Xác suất xạ thủ bắn trúng tấm bia là:
A. \(\frac{{10}}{{19}}\);
B. \(\frac{{10}}{{19}};\)
C. \(\frac{9}{{10}};\)
D. \(\frac{9}{{19}}.\)
Câu 5. Trong hộp có bốn viên bi, trong đó có một viên bi màu vàng, một viên bi màu trắng, một viên bi màu đỏ và một viên bi màu tím. Lấy ngẫu nhiên một viên bi trong hộp. Hỏi có bao nhiêu kết quả xảy ra đối với màu của viên bi được lấy ra?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 6. Hình nào sau đây có trục đối xứng đồng thời có tâm đối xứng?
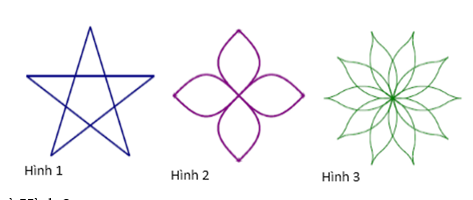
A. Hình 1 và Hình 2;
B. Hình 1 và Hình 3;
C. Hình 2 và Hình 3;
D. Hình 1, Hình 2, Hình 3.
Câu 7. Khẳng định nào sau đây là đúng
A. Góc nhọn là góc có số đo bằng 180°;
B. Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°;
C. Góc nhọn là góc có số đo nhỏ hơn 180°;
D. Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 180°.
Câu 8. Trên hình vẽ, điểm B và D nằm khác phía với mấy điểm?

A. 0;
B. 3;
C. 4;
D. 1.
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \[25\% – 1\frac{1}{4} + 0,2:\frac{6}{5}\];
b) \[\frac{8}{9} + \frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}\];
c) \(\frac{5}{{39}}\,\, \cdot \,\left( {\,7\frac{4}{5}\,\, \cdot \,1\frac{2}{3}\,\, + \,\,8\frac{1}{3}\, \cdot \,7\frac{4}{5}\,} \right)\)
Bài 2. Tìm x biết:
a) \[\frac{{ – 5}}{{12}}:x = \frac{4}{{15}}\];
b) \[\frac{3}{4}x – \frac{2}{3}x = \frac{2}{7}.\frac{1}{6} + \frac{5}{7}.\frac{1}{6}\];
c) 4x – (3 + 5x) = 14.
Bài 3. Lớp \[6A\] có ba loại học sinh: giỏi, khá, trung bình. Trong đó, \[\frac{2}{3}\] số học sinh giỏi là 8 bạn. Số học sinh giỏi bằng 80% số học sinh khá. Số học sinh trung bình bằng \[\frac{7}{9}\] tổng số học sinh khá và học sinh giỏi. Tìm số học sinh của lớp \[6A\]?
Bài 4. Trong một hộp kín có một số quả bóng màu xanh, màu đỏ, màu tím, vàng. Trong một trò chơi, người chơi được lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. Minh thực hiện 100 lần và được kết quả sau:
|
Màu |
Số lần |
|
Xanh |
25 |
|
Đỏ |
23 |
|
Tím |
30 |
|
Vàng |
22 |
Hãy tìm xác suất của thực nghiệm của các sự kiện sau:
a) Minh lấy được quả bóng màu xanh;
b) Quả bóng được lấy ra không là màu đỏ.
Bài 5.
Vẽ đoạn thẳng AB = 8 cm. C là điểm nằm giữa A và B, AC = 3 cm. M là trung điểm của BC. Tính BM.
Bài 6. Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + … + \frac{1}{{{{100}^2}}}\). Chứng minh \(A < \frac{1}{2}\).
Đáp án Đề số 9
Câu 1. Số đối của phân số \(\frac{4}{5}\) là:
A. \(\frac{{ – 4}}{5};\)
B. \(\frac{4}{5};\)
C. \(\frac{5}{4};\)
D. \(\frac{{ – 5}}{4}.\)
Hướng dẫn giải:
Đáp án đúng là: C
Số đối của phân số \(\frac{4}{5}\) là \(\frac{{ – 4}}{5}\) vì \(\frac{{ – 4}}{5} + \frac{4}{5} = 0\).
Câu 2. Biết \[\frac{1}{3}\] quả dưa hấu nặng \(0,8{\rm{ kg}}\).Quả dưa hấu đó nặng là:
A. 3 kg;
B. 3,2 kg;
C. 2,4 kg;
D. 4,2 kg.
Hướng dẫn giải:
Đáp án đúng là: C
Quả dưa hấu đó nặng là \(0,8{\rm{ :}}\frac{{\rm{1}}}{3}{\rm{ = }}\frac{{\rm{4}}}{{\rm{5}}}{\rm{.}}\frac{3}{{\rm{1}}}{\rm{ = }}\frac{{{\rm{12}}}}{{\rm{5}}}{\rm{ = 2,4 kg}}\).
Vậy quả dưa hấu đó nặng 2,4 kg.
Câu 3. Tổng của hai phân số \(\frac{7}{{15}}\) và \(\frac{{ – 2}}{5}\) bằng:
A. \(\frac{5}{{10}}\) ;
B. \(\frac{5}{{20}}\);
C. \(\frac{1}{{15}}\);
D. \[\frac{{ – 1}}{{15}}.\]
Hướng dẫn giải:
Đáp án đúng là: C
Vì: \(\frac{7}{{15}} + \frac{{ – 2}}{5} = \frac{7}{{15}} + \frac{{ – 6}}{{15}} = \frac{{7 + \left( { – 6} \right)}}{{15}} = \frac{1}{{15}}\)
Vậy tổng của hai phân số \(\frac{7}{{15}}\) và \(\frac{{ – 2}}{5}\) bằng \(\frac{1}{{15}}.\)
Câu 4. Một xạ thủ bắn 20 mũi tên vào một tấm bia thì được 18 lần trúng. Xác suất xạ thủ bắn trúng tấm bia là:
A. \(\frac{{10}}{{19}}\);
B. \(\frac{{10}}{{19}};\)
C. \(\frac{9}{{10}};\)
D. \(\frac{9}{{19}}.\)
Hướng dẫn giải:
Đáp án đúng là: C
Tổng số lần thực hiện hoạt động bắn mũi tên vào tấm bia là 20, số lần bắn trúng tấm bia là 18 lần.
Xác suất thực nghiệm bắn trúng bia là: \(\frac{{18}}{{20}} = \frac{9}{{10}}.\)
Câu 5. Trong hộp có bốn viên bi, trong đó có một viên bi màu vàng, một viên bi màu trắng, một viên bi màu đỏ và một viên bi màu tím. Lấy ngẫu nhiên một viên bi trong hộp. Hỏi có bao nhiêu kết quả xảy ra đối với màu của viên bi được lấy ra?
A. 1;
B. 2;
C. 3;
D. 4.
Hướng dẫn giải:
Đáp án đúng là: D
Khi lấy ngẫu nhiên một viên bi, có 4 kết quả có thể xảy ra đối với màu của viên bi được lấy ra, đó là: màu vàng, màu trắng, màu đỏ, màu tím.
Câu 6. Hình nào sau đây có trục đối xứng đồng thời có tâm đối xứng?
A. Hình 1 và Hình 2;
B. Hình 1 và Hình 3;
C. Hình 2 và Hình 3;
D. Hình 1, Hình 2, Hình 3.
Hướng dẫn giải:
Đáp án đúng là: C
Quan sát 3 hình trên a thấy cả ba hình đều có trục đối xứng và tâm đối xứng.
Câu 7. Khẳng định nào sau đây là đúng
A. Góc nhọn là góc có số đo bằng 180°;
B. Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°;
C. Góc nhọn là góc có số đo nhỏ hơn 180°;
D. Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 180°.
Hướng dẫn giải:
Đáp án đúng là: B
Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°.
Câu 8. Trên hình vẽ, điểm B và D nằm khác phía với mấy điểm?

A. 0;
B. 3;
C. 4;
D. 1.
Hướng dẫn giải:
Đáp án đúng là: D
Điểm B và D nằm khác phía so với điểm C.
PHẦN II. TỰ LUẬN
Bài 1. Thực hiện phép tính (tính hợp lí nếu có thể):
a) \[25\% – 1\frac{1}{4} + 0,2:\frac{6}{5}\];
b) \[\frac{8}{9} + \frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}\];
c) \(\frac{5}{{39}}\,\, \cdot \,\left( {\,7\frac{4}{5}\,\, \cdot \,1\frac{2}{3}\,\, + \,\,8\frac{1}{3}\, \cdot \,7\frac{4}{5}\,} \right)\)
Hướng dẫn giải:
a) \[25\% – 1\frac{1}{4} + 0,2:\frac{6}{5}\]
\[ = \frac{{25}}{{100}} – \frac{5}{4} + \frac{1}{5}:\frac{6}{5}\]
\[ = \frac{1}{4} – \frac{5}{4} + \frac{1}{5}.\frac{5}{6}\]
\[ = \left( {\frac{1}{4} – \frac{5}{4}} \right) + \frac{{1.5}}{{5.6}}\]
\[ = \frac{{ – 4}}{4} + \frac{1}{6}\]
\[ = – 1 + \frac{1}{6}\]
\[ = \frac{{ – 6}}{6} + \frac{1}{6}\]
\[ = \frac{{ – 5}}{6}\]
b) \[\frac{8}{9} + \frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}\]
\[ = \frac{8}{9} + \left( {\frac{1}{9}.\frac{2}{9} + \frac{1}{9}.\frac{7}{9}} \right)\]
\[ = \frac{8}{9} + \frac{1}{9}.\left( {\frac{2}{9} + \frac{7}{9}} \right)\]
\[ = \frac{8}{9} + \frac{1}{9}.\frac{9}{9}\]
\[ = \frac{8}{9} + \frac{1}{9}.1\]
\( = \frac{8}{9} + \frac{1}{9}\)
\( = \frac{9}{9}\)
= 1.
a) \(\frac{5}{{39}}{\mkern 1mu} {\mkern 1mu} \, \cdot {\mkern 1mu} \,\left( {{\mkern 1mu} 7\frac{4}{5}\,{\mkern 1mu} {\mkern 1mu} \cdot \,1\frac{2}{3}{\mkern 1mu} {\mkern 1mu} \, + {\mkern 1mu} {\mkern 1mu} \,8\frac{1}{3}\,\, \cdot \,\,7\frac{4}{5}{\mkern 1mu} } \right)\)
\( = \,{\mkern 1mu} \frac{5}{{39}}{\mkern 1mu} {\mkern 1mu} \cdot \,{\mkern 1mu} \left[ {{\mkern 1mu} 7{\mkern 1mu} \frac{4}{5}\,{\mkern 1mu} \cdot \,{\mkern 1mu} \left( {1\frac{2}{3} + {\mkern 1mu} {\mkern 1mu} 8\frac{1}{3}{\mkern 1mu} } \right)} \right]\)
\( = \,{\mkern 1mu} \frac{5}{{39}}{\mkern 1mu} \, \cdot \,\frac{{39}}{5}{\mkern 1mu} \,\left( {1 + \frac{2}{3} + 8 + \frac{1}{3}} \right){\mkern 1mu} \)
\( = \,{\mkern 1mu} {\mkern 1mu} \frac{{5.39}}{{39.5}}{\mkern 1mu} {\mkern 1mu} \cdot\,{\mkern 1mu} \,\left( {9 + \frac{2}{3} + \frac{1}{3}} \right){\mkern 1mu} \)
\( = \,1{\mkern 1mu} \cdot\,\left( {9\, + \frac{3}{3}} \right){\mkern 1mu} \)
= 9 + 1
= 10.
Bài 2. Tìm x biết:
a) \[\frac{{ – 5}}{{12}}:x = \frac{4}{{15}}\];
b) \[\frac{3}{4}x – \frac{2}{3}x = \frac{2}{7}.\frac{1}{6} + \frac{5}{7}.\frac{1}{6}\];
c) 4x – (3 + 5x) = 14.
Hướng dẫn giải
a) \[\frac{{ – 5}}{{12}}:x = \frac{4}{{15}}\]
\[x = \frac{{ – 5}}{{12}}:\frac{4}{{15}}\]
\[x = \frac{{ – 5}}{{12}}.\frac{{15}}{4}\]
\(x = \frac{{ – 5.15}}{{12.4}}\)
\(x = \frac{{ – 5.3.5}}{{3.4.4}}\)
\[x = – \frac{{25}}{{16}}.\]
Vậy \[x = \frac{{ – 25}}{{16}}\].
b) \[\frac{3}{4}x – \frac{2}{3}x = \frac{2}{7}.\frac{1}{6} + \frac{5}{7}.\frac{1}{6}\]
\[\left( {\frac{3}{4} – \frac{2}{3}} \right)x = \frac{1}{6}.\frac{2}{7} + \frac{1}{6}.\frac{5}{7}\]
\[\left( {\frac{9}{{12}} – \frac{8}{{12}}} \right)x = \frac{1}{6}\left( {\frac{2}{7} + \frac{5}{7}} \right)\]
\(\frac{1}{{12}}.x = \frac{1}{6}.\frac{7}{7}\)
\[\frac{1}{{12}}x = \frac{1}{6}\]
\[x = \frac{1}{6}:\frac{1}{{12}}\]
\(x = \frac{1}{6}.\frac{{12}}{1}\)
x = 2.
Vậy x = 2.
c) 4x – (3 + 5x) = 14
4x – 3 – 5x = 14
4x – 5x = 14 + 3
(4 – 5).x = 17
–x = 17
x = –17.
Vậy x = –17.
Bài 3. Lớp \[6A\] có ba loại học sinh: giỏi, khá, trung bình. Trong đó, \[\frac{2}{3}\] số học sinh giỏi là 8 bạn. Số học sinh giỏi bằng 80% số học sinh khá. Số học sinh trung bình bằng \[\frac{7}{9}\] tổng số học sinh khá và học sinh giỏi. Tìm số học sinh của lớp \[6A\]?
Hướng dẫn giải
Số học sinh giỏi của lớp là: \(8:\frac{2}{3} = 12\) (học sinh)
Số học sinh khá của lớp là: 12 : 80% = 15 (học sinh)
Số học sinh trung bình của lớp là: \(\frac{7}{9}.(15 + 12) = 21\) (học sinh)
Số học sinh lớp \[6A\] là: 12 + 15 + 21 = 48 (học sinh).
Bài 4. Trong một hộp kín có một số quả bóng màu xanh, màu đỏ, màu tím, vàng. Trong một trò chơi, người chơi được lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. Minh thực hiện 100 lần và được kết quả sau:
|
Màu |
Số lần |
|
Xanh |
25 |
|
Đỏ |
23 |
|
Tím |
30 |
|
Vàng |
22 |
Hãy tìm xác suất của thực nghiệm của các sự kiện sau:
a) Minh lấy được quả bóng màu xanh;
b) Quả bóng được lấy ra không là màu đỏ.
Hướng dẫn giải:
a) Quan sát bảng ta thấy bóng xanh được lấy 25 lần.
Xác suất của thực nghiệm sự kiện lấy được bóng xanh là: \(\frac{{25}}{{100}} = 0,25\)
b) Quan sát bảng ta thấy bóng đỏ được lấy ra 23 lần.
Do đó số lần Minh không lấy ra bóng đỏ là 100 – 23 = 77 (lần).
Xác suất của thực nghiệm sự kiện lấy ra không là màu đỏ là: \(\frac{{77}}{{100}} = 0,77\)
Bài 5.
Vẽ đoạn thẳng AB = 8 cm. C là điểm nằm giữa A và B, AC = 3 cm. M là trung điểm của BC. Tính BM.
Hướng dẫn giải:

Ta có C là điểm nằm giữa A và B nên AC + BC = AB.
Suy ra BC = AB – AB
Do đó BC = 8 – 3 = 5 cm. \(BC = AB – AC = 7 – 3 = 4cm\).
Vì M là trung điểm BC nên \(BM = \frac{{BC}}{2} = \frac{5}{2} = 2,5\) cm.
Bài 6. Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + … + \frac{1}{{{{100}^2}}}\). Chứng minh \(A < \frac{1}{2}\).
Hướng dẫn giải:
Ta có:
\(A = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + … + \frac{1}{{{{100}^2}}}\)
\( = \frac{1}{{{2^2}}}\left( {1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}}} \right)\).
Mặt khác ta có: \(\frac{1}{{{2^2}}} = \frac{1}{{2.2}} < \frac{1}{{1.2}} = \frac{{2 – 1}}{{1.2}} = \frac{2}{{1.2}} – \frac{1}{{1.2}} = 1 – \frac{1}{2}\)
\(\frac{1}{{{3^2}}} = \frac{1}{{3.3}} < \frac{1}{{2.3}} = \frac{{3 – 2}}{{2.3}} = \frac{3}{{2.3}} – \frac{2}{{2.3}} = \frac{1}{2} – \frac{1}{3}\)
………………..
\(\frac{1}{{{{50}^2}}} = \frac{1}{{50.50}} < \frac{1}{{49.50}} = \frac{{50 – 49}}{{49.50}} = \frac{{50}}{{49.50}} – \frac{{49}}{{49.50}} = \frac{1}{{49}} – \frac{1}{{50}}\)
Do đó \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}} < 1 – \frac{1}{2} + \frac{1}{2} – \frac{1}{3} + … + \frac{1}{{49}} – \frac{1}{{50}}\)
Suy ra \(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}} < 1 – \frac{1}{{50}}\)
\(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}} < \frac{{49}}{{50}} < \frac{{50}}{{50}} = 1\)
\(\frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}} < 1\)
Từ đó ta có: \(1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}} < 1 + 1 = 2\)
\[A = \frac{1}{{{2^2}}}\left( {1 + \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + … + \frac{1}{{{{50}^2}}}} \right) < \frac{1}{4}.2 = \frac{1}{2}\].
Vậy \(A < \frac{1}{2}.\)