Trắc nghiệm Toán lớp 6 Bài 2: Cách ghi số tự nhiên
Phần 1. Trắc nghiệm Cách ghi số tự nhiên
I. Nhận biết
Câu 1. Viết số 27 bằng số La Mã.
A. XXVI.
B. XXVII.
C. XXVIII.
D. XXIV.
Lời giải Chữ số La Mã biểu diễn cho số 27 là XXVII.
Đáp án: B
Câu 2. Trong các số sau: 11 191; 280 901; 12 009 020; 9 126 345. Số nào số 9 ở hàng nghìn.
A. 11 191.
B. 280 901.
C. 12 009 020.
D. 9 126 345.
Lời giải
– Số 11 191, chữ số 9 nằm ở hàng chục.
– Số 280 901, chữ số 9 nằm ở hàng trăm.
– Số 12 009 020, chữ số 9 nằm ở hàng nghìn.
– Số 9 126 345, chữ số 9 nằm ở hàng triệu.
Đáp án: C
Câu 3. Hai mươi chín nghìn sáu trăm linh ba là số nào?
A. 26 903.
B. 29 603.
C. 23 609.
D. 20 603.
Lời giải Hai mươi chin nghìn sáu trăm linh ba là số: 29 603
Đáp án: B
Câu 4. Biểu diễn các chữ số La Mã: XXI, XXII, XIX bằng các số tự nhiên lần lượt là:
A. 21; 22 và 19.
B. 22; 21 và 19.
C. 19; 21 và 22.
D. 21; 19 và 22.
Lời giải
XXI biểu diễn cho số 21;
XXII biểu diễn cho số 22;
XIX biểu diễn cho số 19.
Đáp án: A
Câu 5. Cho số 23 473 872. Số triệu của số này là:
A. 3
B. 23 000 000
C. 20 000 000
D. 2
Lời giải Số triệu của số 23 473 872 là 23 000 000.
Đáp án: B
Câu 6. Trong số 43 256 chữ số 3 nằm ở hàng nào?
A. Hàng chục.
B. Hàng trăm.
C. Hàng nghìn.
D. Hàng chục nghìn.
Lời giải Trong số 43 256 số 3 nằm ở hàng nghìn.
Đáp án: C
Câu 7. Số La Mã IV biểu diễn cho số tự nhiên:
A. 4.
B. 5.
C. 14.
D. 9.
Lời giải Số La Mã IV biểu diễn cho số 4.
Đáp án: A
Câu 8. Nêu cách đọc số 123 875.
A. Một hai ba nghìn tám bảy năm.
B. Một trăm hai ba nghìn tám trăm bảy mươi lăm.
C. Một trăm nghìn hai ba tám trăm bảy năm.
C. Một trăm hai ba nghìn bảy trăm tám mươi lăm.
Lời giải Cách đọc số 123 875 là: Một trăm hai mươi ba nghìn tám trăm bảy mươi lăm.
Đáp án: B
Câu 9. Cho số 8 763. Số chục của số này là:
A. 6.
B. 63.
C. 8 760.
D. Đáp án khác.
Lời giải Trong số 8 763 số chục là 8 760
Đáp án: C
Câu 10. Chữ số 7 trong số 7 110 385 có giá trị là bao nhiêu?
A. 7 000 000.
B. 7 000.
C. 700.
D. 7.
Lời giải Chữ số 7 trong số 7 110 385 nằm ở hàng triệu và có giá trị là 7 x 1000 000 = 7 000 000.
Đáp án: A
II. Thông hiểu
Câu 1. Viết số 43 406 thành tổng giá trị các chữ số của nó.
A. 43 406 = 4 + 3 + 4 + 0 + 6.
B. 43 406 = 4×1 000 + 3×100 + 4×10 + 6.
C. 43 406 = 4×10 000 + 3×1 000 + 4×100 + 0x10 + 6.
D. 43 406 = 43×100 + 406.
Lời giải
Số 43 406 được viết thành tổng giá trị các chữ số của nó là:
43 406 = 4×10 000 + 3×1 000 + 4×100 + 0x10 + 6.
Đáp án: C
Câu 2. Một số tự nhiên có 6 chữ số được viết bởi ba chữ số 0 và ba chữ số 9 nằm xen kẽ nhau. Đó là số nào?
A. 090 909.
B. 909 909.
C. 909 090.
D. 909 009.
Lời giải
Số tự nhiên có sáu chữ số từ ba số 0 và ba số 9.
Nếu số 0 nằm ở chữ số đầu tiên thì ta chỉ có số có 5 chữ số. Do đó số đầu tiên phải là số 9.
Vì 0 và 9 nằm xen kẽ nhau nên số cần viết là 909 090.
Đáp án: C
Câu 3. Một số được viết dưới dạng tộng các chữ số là: 8×10 000 + 9×100 + 2×10. Số đó là số nào?
A. 89 020
B. 89 200
C. 80 902
D. 80 920
Lời giải Ta có 8×10 000 + 9×100 + 2×10 = 80 920.
Đáp án: D
Câu 4. Chỉ dùng bốn chữ số 0; 2; 3. Có tất cả bao nhiêu số tự nhiên có ba chữ số mà mỗi chữ số chỉ viết một lần.
A. 2
B. 4
C. 6
D. 8.
Lời giải
Vì số 0 không thể năm ở hàng trăm nên chữ số hàng trăm chỉ có thể là 2 hoặc 3. Do đó ta có tất cả các số tự nhiên có ba chữ số được lập từ ba chữ số 0; 2 và 3 là
203; 230; 302; 320.
Đáp án: C
III. Vận dụng
Câu 1. Dùng các chữ số 0; 3; 5, viết một số tự nhiên có ba chữ số khác nhau mà chữ số 5 có giá trị 50.
A. 350
B. 305
C. 503
D. 530
Lời giải
Vì chữ số 5 có giá trị 50 nghĩa là chữ số 5 ở hàng chục.
Còn chữ số hàng trăm không thể bằng 0 nên chữ số hàng trăm là chữ số 3.
Còn lại chữ số hàng đơn vị là 0.
Vậy số cần tìm là 350.
Đáp án: A
Câu 2. Trong một cửa hàng bánh kẹo, người ta đóng gói kẹo thành các loại: mỗi gói có 10 cái kẹo; mỗi hộp có 10 gói; mỗi thùng có 10 hộp. Một người mua 9 thùng, 9 hộp và 9 gói kẹo. Hỏi người đó đã mua tất cả bao nhiêu cái kẹo?
A. 9 999
B. 9 090
C. 9 009
D. 9 990
Lời giải
Mỗi thùng có số cái kẹo là: 10x10x10 = 1000.
Mỗi hộp có số kẹo là: 10×10 = 100.
Một người mua 9 thùng, 9 hộp và 9 gói kẹo thì người đó đã mua được:
9×1000 + 9×100 + 9×10 = 9 990 (cái kẹo).
Vậy người đó đã mua được tất cả 9 990 cái kẹo.
Đáp án: D
Câu 3. Bác Hoa đi chợ. Bác chỉ mang ba loại tiền: loại (có mệnh giá) 1 nghìn (1 000) đồng, loại 10 nghìn (10 000) đồng và loại 100 nghìn (100 000) đồng. Tổng số tiền bác phải trả là 492 nghìn đồng. Nếu mỗi loại tiền, bác mang theo không quá 9 tờ thì bác phải trả bao nhiêu tờ tiền mỗi loại, mà người bán không phải trả lại tiền thừa.
A. 5 tờ 100 nghìn đồng, 9 tờ 10 nghìn đồng, 1 tờ 1 nghìn đồng.
B. 5 tờ 100 nghìn đồng, 9 tờ 10 nghìn đồng, 2 tờ 1 nghìn đồng.
C. 4 tờ 100 nghìn đồng, 9 tờ 10 nghìn đồng, 1 tờ 1 nghìn đồng.
D. 4 tờ 100 nghìn đồng, 9 tờ 10 nghìn đồng, 2 tờ 1 nghìn đồng.
Lời giải
Ta có: 492 = 4.100 + 9.10 + 2.
Bác Hoa trả 4 tờ 100 nghìn đồng, 9 tờ 10 nghìn đồng và 2 tờ 1 nghìn thì người bán không phải trả lại tiền thừa.
Đáp án: D
Phần 2. Lý thuyết Cách ghi số tự nhiên
1. Hệ thập phân
+ Cách ghi số tự nhiên trong hệ thập phân
– Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.
– Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …
Chú ý: Khi viết các số tự nhiên ta quy ước:
1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.
2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.
Ví dụ 1. Hãy viết tất cả các số tự nhiên có ba chữ số khác nhau chỉ dùng 3 chữ số 0; 3; 5. Đọc mỗi số đã viết được.
Lời giải
Các số tự nhiên có ba chữ số khác nhau từ ba số 0; 3; 5 là:
305; 350; 503; 530.
Cách đọc:
305: ba trăm linh năm;
350: ba trăm năm mươi;
503: năm trăm linh ba;
530: năm trăm ba mươi.
+ Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó. Chẳng hạn như số có ba chữ số 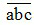 (a, b, c ∈ N) được viết dưới dạng tổng giá trị các chữ số của nó như sau:
(a, b, c ∈ N) được viết dưới dạng tổng giá trị các chữ số của nó như sau: 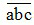 = a x 100 + b x 10 + c
= a x 100 + b x 10 + c
Ví dụ 2.
a) Viết sô 32009 thành tổng các chữ số của chúng.
c) Cho số 1256934, chữ số 5 trong số đã cho nằm ở hàng nào và có giá trị bao nhiêu?
Lời giải
a) 32009 = 3 x 10000 + 2 x 1000 + 0 x 100 + 0 x 10 + 9.
b) Chữ số 5 trong số đã cho nằm ở hàng chục nghìn và có giá trị .
2. Số La Mã
Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).
Ba chữ số đó cộng với hai cụm chữ số là IV và IX là năm thành phần dùng để ghi số La Mã.
Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:
|
Thành phần |
I |
V |
X |
IV |
IX |
|
Giá trị (viết trong hệ thập phân) |
1 |
5 |
10 |
4 |
9 |
+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:
|
XI |
XII |
XIII |
XIV |
XV |
XVI |
XVII |
XVIII |
XIX |
XX |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:
|
XXI |
XXII |
XXIII |
XXIV |
XXV |
XXVI |
XXVII |
XXVIII |
XXIX |
XXX |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Ví dụ 3:
a) Viết các số 17; 23 và 8 bằng số La Mã.
b) Đọc các số La Mã XXIX, XIV, VII.
Lời giải
a) Số La Mã biểu diễn cho số 17 là: XVII;
Số La Mã biểu diễn cho số 23 là: XXIII;
Số La Mã biểu diễn cho số 8 là: VIII.
b) Đọc:
XXIX: Hai mươi chín;
XIV: Mười bốn;
VII: Bảy.
Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:
Trắc nghiệm Bài 1: Tập hợp
Trắc nghiệm Bài 2: Cách ghi số tự nhiên
Trắc nghiệm Bài 3: Thứ tự trong tập hợp các số tự nhiên
Trắc nghiệm Bài 4: Phép cộng và phép trừ số tự nhiên
Trắc nghiệm Bài 5: Phép nhân và phép chia số tự nhiên