Trắc nghiệm Toán lớp 6 Chương 1: Tập hợp các số tự nhiên
Phần 1. Trắc nghiệm Chương 1: Tập hợp các số tự nhiên
I. Nhận biết
Câu 1. Trong phép tính mà chỉ chứa phép nhân và phép chia thì thứ tự thực hiện phép tính như thế nào?
A. Nhân trước, chia sau.
B. Chia trước, nhân sau.
C. Thực hiện lần lượt từ phải sang trái.
D. Thực hiện lần lượt từ trái sang phải.
Lời giải Trong phép tính mà chỉ chứa phép nhân và phép chia thì thực hiện lần lượt từ trái sang phải.
Đáp án: D
Câu 2. Trong số 723 650, chữ số 5 có giá trị bao nhiêu?
A. 5 là chữ số hàng chục.
B. 5 có giá trị 5.10 = 50.
C. 5 có giá trị 723 65.
D. 5 có giá trị 5.
Lời giải Trong số 723 650 chữ số 5 có hàng chục và có giá trị là 5.10 = 50.
Đáp án: B
Câu 3. Trong số nào dưới đây, chữ số 7 nằm ở hàng nghìn.
A. 127 000 000.
B. 870 900.
C. 547.
D. 7 200.
Lời giải
+) Số 127 000 000, chữ số 7 nằm ở hàng triệu.
+) Số 870 900 090, chữ số 7 nằm ở hàng chục nghìn.
+) Số 547, chữ số 7 nằm ở hàng đơn vị.
+) Số 7 200, chữ số 7 nằm ở hàng nghìn.
Đáp án: D
Câu 4. “Chín bình phương” là cách đọc của số nào dưới đây?
A. 93;
B. 92;
C. 9.2;
D. 94.
Lời giải Chín bình phương là cách đọc của số 92.
Đáp án: B
Câu 5. Kết quả của phép nhân 125.8.
A. 10;
B. 100;
C. 1000;
D. 200.
Lời giải 125.8 = 1000.
Đáp án: C
Câu 6: Cho tập hợp N = {2, 4, 6, 8}, có bao nhiêu phần tử trong tập hợp N?
A. 1
B. 2
C. 3
D. 4
Lời giải Tập hợp N có 4 phần tử là: 2; 4; 6; 8.
Đáp án: D
Câu 7: A là tập hợp các số tự nhiên nhỏ hơn hoặc bằng 5. Hãy viết tập hợp A bằng các liệt kê.
A. A = {1; 2; 3; 4; 5}.
B. A = {1; 2; 3; 4}.
C. A = {0; 1; 2; 3; 4; 5}.
D. A = {0; 1; 2; 3; 4}.
Lời giải
Các số tự nhiên nhỏ hơn hoặc bằng 5 bao gồm: 0; 1; 2; 3; 4; 5.
Vậy A = {0; 1; 2; 3; 4; 5}.
Đáp án: C
Câu 8: Điền vào chỗ trống để có được ba số tự nhiên liên tiếp tăng dần : 49, …., ….
A. 50; 51.
B. 51; 53.
C. 48; 47.
D. 59; 69.
Lời giải Ba số tự nhiên liên tiếp tăng dần: 49; 50; 51.
Đáp án: A
Câu 9: Số La Mã biểu diễn số 29 là?
A. XIX;
B. XXIX;
C. XXXI;
D. XXVIV.
Lời giải Số La Mã biểu diễn cho số 29 là: XXIX.
Đáp án: B
Câu 10: B là tập hợp các chữ cái trong từ “TAP HOP”, vậy B =?
A. B = {T; A; P; H; O; P}.
B. B = {T; A; P; H}.
C. B = {T; A; P; H; O}.
D. B = {T; P; H; O}.
Lời giải
Các chữ cái trong từ tập hợp: T; A; P; H; O; P.
Vì trong tập hợp mỗi phần tử chỉ được liệt kê 1 lần nên B = {T; A; P; H; O}.
Đáp án: C
II. Thông hiểu
Câu 1. Đưa kết quả phép tính 122 + 32 về dưới dạng một lũy thừa cơ số 15 với số mũ là:
A. 1;
B. 2;
C. 3;
D. 4.
Lời giải
122 + 32 = 144 + 81 = 225.
225 = 15.15 = 152.
Vậy số mũ là 2.
Đáp án: B
Câu 2. Cho biểu thức 7x3 – (8y)2. Tính giá trị biểu thức tại x = 3 và y =1.
A. 189;
B. 64;
C. 125;
D. 115.
Lời giải
Thay x = 3 và y = 1 vào biểu thức 7x3 – (8y)2, ta được:
7.33 – (8.1)2 = 7.27 – 82 = 189 – 64 = 125.
Đáp án: C
Câu 3. Ghép mỗi phép tính ở cột A với lũy thừa tương ứng của nó ở cột B:
|
Cột A |
Cột B |
|
1. 37.33 |
a. 517 |
|
2. 59:57 |
b. 23 |
|
3. 211:28 |
c. 310 |
|
4. 512.55 |
d.52 |
A. 1 – c; 2 – d; 3 – b; 4 – a.
B. 1 – c; 2 – b; 3 – d; 4 – a.
C. 1 – a; 2 – d; 3 – b; 4 – c.
D. 1 – a; 2 – b; 3 – d; 4 – c.
Lời giải
Ta có: 37.33 = 37+3 = 310
59:57 = 59-7 = 52
211:28 = 211-8 = 23
512.55 = 512+5 = 517
Vậy 1 – c; 2 – d; 3 – b; 4 – a.
Đáp án: A
Câu 4. Theo Tổng cục Thống kê, tháng 10 năm 2020 dân số được làm tròn là 98 000 000 người. Em hãy viết dân số của Việt Nam dưới dạng tích của một số với một lũy thừa của 10.
A. 98.106;
B. 98.105;
C. 98.104;
D. 98.103.
Lời giải
Ta có: 98 000 000 = 98.106 (người).
Vậy dân số Việt Nam năm 2020 là: 98.106 người.
Đáp án: A
Câu 5. Tính một cách hợp lý: 30.40.50.60
A. 3 600;
B. 3 600 000;
C. 36 000;
D. 360 000.
Lời giải
Ta có: 30.40.50.60
= (30.60).(40.50)
= 1 800.2 000
=3 600 000.
Đáp án: B
Câu 6. Viết gọn tích sau dưới dạng một lũy thừa: 2.3.36.
A. 23.33;
B. 63;
C. 62;
D. 22.32.
Lời giải Ta có: 2.3.36 = 2.3.6.6 = 6.6.6 = 63.
Đáp án: B
Câu 7. Thực hiện phép tính: 110 – 72 + 22:2 ?
A. 72;
B. 107;
C. 41 (dư 1);
D. 62.
Lời giải
110 – 72 + 22:2
= 110 – 49 + 11
= 61 + 11
= 72.
Đáp án: A
Câu 8. Giá trị của biểu thức C là: C = 23.3 – (110 + 15) : 42
A. C = 23;
B. C = 24;
C. C = 25;
D. C = 26.
Lời giải
C = 23.3 – (110 + 15) : 42
= 8.3 – (1+15) : 16
= 24 – 16:16
= 24 -1
= 23.
Đáp án: A
Câu 9. Tìm số tự nhiên x, thỏa mãn: (75:3 + 2.92):x = 11.
A. x = 11;
B. x = 17;
C. x = 14;
D. x = 16.
Lời giải
(75:3 + 2.92):x = 11
(25 + 162):x = 11
187:x = 11
x = 187: 11
x = 17.
Đáp án: A
Câu 10. Cho tập hợp M = {x ∈ N* | 2x + 5 = 5}. Số phần tử của tập hợp M là:
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Xét 2x + 5 = 5
2x = 5 – 5
2x = 0
x = 0.
Mà x ∈ N* nên x = 0 (loại).
Vậy tập hợp M không có phần tử nào.
Đáp án: A
III. Vận dụng
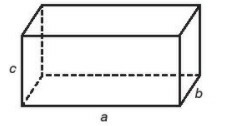
Câu 1. Viết biểu thức tính diện tích toàn phần của hình hộp chữ nhật (hình dưới) theo a, b, c. Tính giá trị của biểu thức đó khi a = 5cm; b = 4cm; c = 3cm.
A. 54 cm2;
B. 94 cm2;
C. 40 cm2;
D. 84 cm2.
Lời giải
Diện tích xung quanh của hình hộp chữ nhật là: 2.c.(a + b)
Diện tích đáy của hình hộp chữ nhật là: a.b
Diện tích toàn phần của hình hộp chữ nhật là: Stp = Sxq + 2Sday = 2.c.(a+b) + 2.a.b
Khi a = 5cm, b = 4cm, c = 3cm thì diện tích toàn phần của hình hộp chữ nhật là:
2.c.(a+b) + 2.a.b = 2. 3. ( 5 + 4) + 2. 5 . 4 = 6.9 + 40 = 54 + 40 = 94 (cm2)
Vậy diện tích của hình hộp chữ nhật là 94 (cm2).
Đáp án: B
Câu 2. Khối 6 có 320 học sinh đi tham quan. Nhà trường cần thuê ít nhất bao nhiêu xe ô tô 45 chỗ ngồi để đủ chỗ cho tất cả học sinh?
Lời giải
Vì 320 : 45 = 7 (dư 5) nên xếp đủ 7 xe thì còn dư 5 học sinh, do đó cần thêm 1 xe để chở hết 5 học sinh đó.
Vậy cần tất cả: 7 + 1 = 8 (xe ô tô)
Câu 3. Một phòng chiếu phim có 18 hàng ghế, mỗi hàng ghế có 18 ghế. Giá một vé xem phim là 50 000 đồng. Tối thứ Sáu, số tiền bán vé thu được là 10 550 000 đồng. Hỏi có bao nhiêu vé không bán được?
A. 324 vé;
B. 112 vé;
C. 113 vé;
D. 115 vé.
Lời giải
Số ghế của phòng chiếu phim là: 18.18 = 324 (ghế)
Như ta thấy, mỗi ghế sẽ tương ứng với 1 vé xem phim nên số vé nhiều nhất có thể bán được là 324 vé.
Số vé bán được trong tối thứ Sáu là: 10 550 000: 50 000 = 211 (vé).
Số vé không bán được trong tối thứ Sáu là: 324 – 211 = 113 (vé).
Đáp án: C
Câu 4. Tính giá trị của biểu thức: .
A. 210;
B. 2 100;
C. 1 890;
D. 1 980.
Lời giải
21.[(1 245 + 987):23 – 15.12] + 21
= 21.[2 232:8 – 180] + 21
= 21.[279 – 180] + 21
= 21.99 + 21
= 21(99 + 1)
= 21.100
= 2 100.
Đáp án: B
Câu 5. Nhóm Lan dự định thực hiện một kế hoạch nhỏ với số tiền cần có là 200 000 đồng. Hiện tại các bạn đang có 80 000 đồng. Các bạn cần thực hiện gây quỹ thêm bằng cách thu lượm và bán giấy vụn, mỗi tháng được 20 000 đồng. Số tiền còn thiếu cần phải thực hiện gây quỹ trong mấy tháng?
A. 4 tháng;
B. 5 tháng;
C. 6 tháng;
D. 7 tháng.
Lời giải
a) Số tiền hiện tại các bạn còn thiếu là 200000 – 80000 = 120000 đồng.
Vậy số tiền hiện tại các bạn còn thiếu là 120 000 đồng.
b) Số tiền còn thiếu cần phải thực hiện gây quỹ trong số tháng là: 120000 : 20000 = 6 tháng.
Vậy cần phải thực hiện gây quỹ trong 6 tháng.
Đáp án: C
Phần 2. Lý thuyết Chương 1: Tập hợp các số tự nhiên
I. Tập hợp
1. Tập hợp và phần tử của tập hợp
Tập hợp là một khái niệm cơ bản của toán học (không định nghĩa).
Tập hợp được kí hiệu là các chữ cái in hoa: A, B, C, D, …
2. Mô tả một tập hợp
2.1. Liệt kê các phần tử của tập hợp
Viết tất cả các phần tử của tập hợp trong dấu {} theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
2.1. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
Gọi x là phần tử của tập hợp, tìm các tính chất đặc trưng của các phần tử.
II. Cách ghi số tự nhiên
1. Hệ thập phân
Cách ghi số tự nhiên trong hệ thập phân
– Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.
– Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …
Chú ý: Khi viết các số tự nhiên ta quy ước:
1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.
2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.
Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó.
2. Số La Mã
Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).
Ba chữ số đó cộng với hai cụm chữ số là IV và Ĩ là năm thành phần dùng để ghi số La Mã.
Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:
|
Thành phần |
I |
V |
X |
IV |
IX |
|
Giá trị (viết trong hệ thập phân) |
1 |
5 |
10 |
4 |
9 |
+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:
|
XI |
XII |
XIII |
XIV |
XV |
XVI |
XVII |
XVIII |
XIX |
XX |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:
|
XXI |
XXII |
XXIII |
XXIV |
XXV |
XXVI |
XXVII |
XXVIII |
XXIX |
XXX |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
III. Thứ tự trong tập hợp các số tự nhiên
Ta đã biết tập các số tự nhiên được kí hiệu là N, nghĩa là N = . Mỗi phần tử 0; 1; 2; 3; … được biểu diễn bởi một điểm trên tia số gốc 0 như hình vẽ:
Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì trên tia số nằm ngang điểm a nằm bên trái điểm b. Khi đó, ta viết a < b hoặc b > a. Ta còn nói: điểm a nằm trước điểm b, hoặc điểm b nằm sau điểm a.
Mỗi số tự nhiên có đúng một số liền sau, chẳng hạn 9 là số liền sau của 8 (còn 8 là số liền trước của 9). Hai số 8 và 9 là hai số tự nhiên liên tiếp.
Nếu a < b và b < c thì a < c (tính chất bắc cầu). Chẳng hạn a < 5 và 5 < 7 suy ra a < 7.
Kí hiệu ≤ và ≥
Ta còn dùng kí hiệu a ≤ b (đọc là “a nhỏ hơn hoặc bằng b”) để nói “a < b hoặc a = b”.
Ta còn dùng kí hiệu a ≥ b (đọc là “a lớn hơn hoặc bằng b”) để nói “a > b hoặc a = b”.
Tính chất bắc cầu còn có thể viết: nếu a ≤ b và b ≤ c thì a ≤ c .
IV. Phép cộng và phép trừ số tự nhiên
1. Phép cộng số tự nhiên
Phép cộng hai số tự nhiên a và b cho ta một số tự nhiên gọi là tổng của chúng, kí hiệu là a + b.
Có thể minh họa phép cộng nhờ tia số, chẳng hạn phép cộng 3 + 4 = 7
Phép cộng số tự nhiên có các tính chất:
Giáo hoán: a + b = b + a.
Kết hợp: (a + b) + c = a + (b + c).
Chú ý: a + 0 = 0 + a = a.
Tổng (a + b) + c hay a + (b + c) gọi là tổng của ba số a, b, c và viết gọn là: a + b + c.
2. Phép trừ số tự nhiên
Với hai số tự nhiên a, b đã cho, nếu có số tự nhiên c sao cho a + b = c thì ta có phép trừ
a – b = c.
Trong đó, a là số bị trừ, b là số trừ và c là hiệu.
V. Phép nhân và phép chia số tự nhiên
Phép nhân hai số tự nhiên a và b cho ta một số tự nhiên c được gọi là tích. Kí hiệu: a.b = c (hoặc a x b = c)
Trong đó: a và b là hai thừa số, c là tích.
Chú ý nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không nhân giữa các thừa số. Chẳng hạn: x.y = xy; 5.m = 5m; …
VI. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an =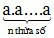 
(n ∈ N*)
an đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.
Chú ý: Ta có a1 = a.
a2 cũng được gọi là a bình phương (hay bình phương của a);
a3 cũng được gọi là a lập phương (hay lập phương của a).
VII. Thứ tự thực hiện các phép tính
Đối với các biểu thức không có dấu ngoặc:
– Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.
– Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
Đối với các biểu thức có dấu ngoặc:
– Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.
– Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.
Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:
Chương 1: Tập hợp các số tự nhiên
Chương 2: Tính chia hết trong tập hợp các số tự nhiên
Chương 3: Số nguyên
Chương 4: Một số hình phẳng trong thực tiễn
Chương 5: Tính đối xứng của hình phẳng trong tự nhiên