Chuyên đề Các phép toán với phân số lớp 5 hay, chọn lọc

Chuyên đề Các phép toán với phân số lớp 5

I/ Lý thuyết

– Các phép toán liên quan đến phân số đó là các phép toán: Cộng, trừ, nhân, chia, phân số.

II/ Các dạng bài tập

II.1/ Dạng 1: Phép cộng phân số

1. Phương pháp giải

Phép cộng phân số được chia ra làm 2 dạng nhỏ:

– Cộng phân số cùng mẫu số: Ta cộng tử số với nhau và giữ nguyên mẫu số.

– Cộng phân số khác mẫu số: Ta quy đồng mẫu số các phân số, rồi cộng các phân số đó lại với nhau.

2. Ví dụ minh họa

Bài 1: Tính: $\frac{5}{6}+\frac{9}{6}$

Ta thấy hai phân số này cùng mẫu số là 6 nên ta cộng 2 tử số với nhau và giữ nguyên mẫu số.

Ta có thể trình bày như sau:

$\frac{5}{6}+\frac{9}{6}=\frac{5+9}{6}=\frac{14}{6}$

Bài 2: Tính: $\frac{9}{4}+\frac{4}{5}$

Ta thấy hai phân số này khác mẫu số, do đó ta cần quy đồng mẫu số rồi cộng 2 phân số đó với nhau.

Ta có thể trình bày như sau:

$\frac{9}{4}+\frac{4}{5}=\frac{45}{20}+\frac{16}{20}=\frac{61}{20}$

Bài 3: Tính: $3+\frac{2}{5}$

Phép tính này thuộc dạng 1 số tự nhiên cộng phân số. Ta chuyển số tự nhiên dưới dạng phân số có mẫu số bằng 1. Rồi tiến hành quy đồng và cộng 2 phân số như bình thường: $3+\frac{2}{5}=\frac{3}{1}+\frac{2}{5}=\frac{15}{5}+\frac{2}{5}=\frac{17}{5}$

Khi đã làm thành thạo các bước, chúng ta có thể rút gọn lại như sau: $3+\frac{2}{5}=\frac{15}{5}+\frac{2}{5}=\frac{17}{5}$ 

II.2/ Dạng 2: Phép trừ phân số

1. Phương pháp giải

Phép trừ phân số được chia ra làm 2 dạng nhỏ:

– Trừ phân số cùng mẫu số: Ta trừ tử số với nhau và giữ nguyên mẫu số.

– Trừ phân số khác mẫu số: Ta quy đồng mẫu số các phân số, rồi trừ các phân số đó lại với nhau.

2. Ví dụ minh họa

Bài 1: Tính: $\frac{15}{6}-\frac{7}{6}$

Ta thấy 2 phân số này cùng mẫu số, nên ta trừ 2 tử số cho nhau và giữ nguyên mẫu số.

Ta có thể trình bày như sau: $\frac{15}{6}-\frac{7}{6}=\frac{15-7}{6}=\frac{8}{6}$ 

Bài 2: Tính: $\frac{5}{9}-\frac{3}{10}$ 

Ta thấy, 2 phân số này khác mẫu số, nên ta quy đồng mẫu số 2 phân số rồi trừ 2 phân số đó với nhau.

Ta có thể trình bày như sau:

$\frac{5}{9}-\frac{3}{10}=\frac{50}{90}-\frac{27}{90}=\frac{23}{90}$

Bài 3: Tính: $5-\frac{2}{3}$ 

Phép tính này thuộc dạng 1 số tự nhiên trừ phân số. Ta chuyển số tự nhiên dưới dạng phân số có mẫu số bằng 1. Rồi tiến hành quy đồng và trừ 2 phân số như bình thường.

$5-\frac{2}{3}=\frac{5}{1}-\frac{2}{3}=\frac{15}{3}-\frac{2}{3}=\frac{13}{3}$

Khi đã làm thành thạo thì chúng ta có thể làm ngắn gọn như sau: $5-\frac{2}{3}=\frac{15}{3}-\frac{2}{3}=\frac{13}{3}$

II.3/ Dạng 3: Phép nhân phân số

1. Phương pháp giải

-Muốn nhân các phân số với nhau, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

2. Ví dụ minh họa

Bài 1: Tính: $\frac{2}{5}\times \frac{7}{8}$  

Áp dụng đúng quy tắc nhân phân số để làm:

$\frac{2}{5}\times \frac{7}{8}=\frac{2\times 7}{5\times 8}=\frac{14}{40}$ 

Bài 2: Tính: $\frac{8}{12}\times 3$  

Phép tính này thuộc dạng 1 số tự nhiên nhân phân số. Ta chuyển số tự nhiên dưới dạng phân số có mẫu số bằng 1. Rồi nhân 2 phân số như bình thường.

$\frac{8}{12}\times 3=\frac{8}{12}\times \frac{3}{1}=\frac{8\times 3}{12\times 1}=\frac{24}{12}$

Khi đã làm thành thạo chúng ta có thể làm rút gọn như sau: $\frac{8}{12}\times 3=\frac{8\times 3}{12}=\frac{24}{12}$ 

II.4/ Dạng 4: Phép chia phân số

1. Phương pháp giải

– Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

– Phân số đảo ngược là phân số đảo ngược tử số thành mẫu số, mẫu số thành tử số.

Ví dụ: Phân số đảo ngược của $\frac{2}{3}\mathrm{là}\frac{3}{2}$

2. Ví dụ minh họa

Bài 1: Tính: $\frac{5}{7}:\frac{3}{4}$  

Ta áp dụng đúng quy tắc để làm bài:

$\frac{5}{7}:\frac{3}{4}=\frac{5}{7}\times \frac{4}{3}=\frac{20}{21}$  

Bài 2: Tính: a) $3:\frac{2}{5}$              b) $\frac{3}{7}:2$  

a) Phép tính này dưới dạng số tự nhiên chia cho phân số. Ta giữ nguyên số thứ nhất rồi nhân với đảo ngược của phân số thứ 2. $3:\frac{2}{5}=3\times \frac{5}{2}=\frac{3\times 5}{2}=\frac{15}{2}$ 

b) Phép tính này dưới dạng phân số chia cho số tự nhiên. Ta có thể chuyển số tự nhiên dưới dạng phân số có mẫu số bằng 1. Sau đó thực hiện chia phân số như bình thường: $\frac{3}{7}:2=\frac{3}{7}:\frac{2}{1}=\frac{3}{7}\times \frac{1}{2}=\frac{3}{14}$

Khi đã làm thành thạo, ta có thể rút gọn như sau:

 $\frac{3}{7}:2=\frac{3}{7\times 2}=\frac{3}{14}$

III/ Bài tập vận dụng

Bài 1: Tính:

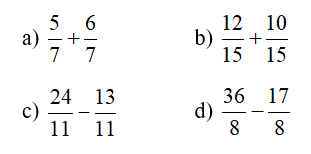
Bài 2: Tính:

 

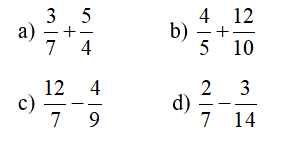
Bài 3: Tính:

 

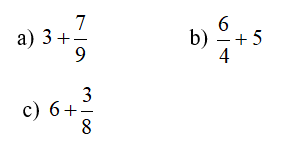
Bài 4: Tính:

 

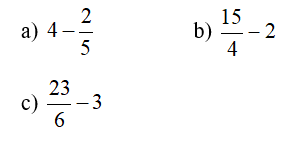
Bài 5: Tính:

a) $\frac{2}{9}\times \frac{7}{12}$                 b) $\frac{3}{11}\times \frac{12}{5}$ 

c) $3\times \frac{7}{9}$                     d) $\frac{4}{15}\times 6$  

Bài 6: Tính:

a) $\frac{4}{5}:\frac{3}{7}$                     b) $\frac{2}{9}:\frac{7}{11}$

c) $\frac{5}{13}:\frac{4}{9}$ 

Bài 7: Tính:

a) $\frac{5}{2}:3$                     b) $5:\frac{6}{7}$   

c) $\frac{8}{12}:7$  

Bài 8: Rút gọn rồi tính:

a) $\frac{5}{15}+\frac{48}{16}$                  b) $\frac{6}{9}:\frac{12}{36}$ 

c) $\frac{4}{12}\times \frac{56}{14}$  

Bài 9: Tính rồi rút gọn:

a) $\frac{2}{7}:\frac{4}{5}$                         b) $\frac{8}{21}:\frac{4}{7}$ 

c) $\frac{3}{8}\times \frac{4}{9}$  

Bài 10: Tính:

 a) $\frac{5}{2}\times \frac{1}{3}+\frac{1}{4}$       

b) $\frac{6}{5}+\frac{3}{5}:2$  

Bài 11: Tính rồi rút gọn :

Bài 12: Tính:

Bài 13: Tính:

Bài 14: Tính:

Bài 15: Tính tổng:

Bài 16: Rút gọn rồi tính:

Bài 17: Tính tổng:

Bài 18: Tính tổng:

Bài 19: Tính bằng cách thuận tiện nhất:

Bài 20: Tìm phân số viết vào chỗ chấm để có:

Bài 21: Một ô tô ngày đầu đi được 1/4 quãng đường , ngày hôm sau đi được 1/2 quãng đường đó. Hỏi cả ngày ô tô đi được tất cả mấy phần quãng đường đó?

Bài 22: Mỗi tiết học kéo dài 2/3 giờ. Giữa hai tiết học, học sinh được nghỉ 1/6 giờ. Hỏi thời gian một tiết học và giờ nghỉ kéo dài trong bao lâu?

Bài 23: Hộp thứ nhất đựng 1/4 kg kẹo. Hộp thứ hai đựng nhiều hơn hộp thứ nhất 1/5 kg kẹo. Hỏi cả hai hộp đựng bao nhiêu ki-lô-gam kẹo?

Bài 24: Một tấm kính hình chữ chữ nhật có chiều dài 4/5 m, chiều rộng 1/2 m. Tính diện tích tấm kính đó.

Bài 25: Người ta hòa 1/2 l si-rô nho vào 7/4 l nước lọc để pha nước nho. Rót đều nước nho đó vào các cốc, mỗi cốc chứa 1/4 l . Hỏi rót được mấy cốc nước nho?

Bài 26: a, Tính diện tích của hình chữ nhật biết chiều rộng bằng m và chu vi của hình chữ nhật bằng m

b, Diện tích của hình chữ nhật bằng m2, chiều rộng là m. Tính chu vi của hình chữ nhật đó

Bài 27: So sánh hai phân số

và 

Bài 28: Kết quả của phép tính  là:

A. 

B. 

C. 

D. 

Bài 29:  Kết quả của phép tính  là:

A. 4

B. 3

C.  2

D. 1

Bài 30: Tìm X, biết :

A. 

B. 

C. 

D.