Bài tập Toán 5 Chương 1 Bài 2: Ôn tập Tính chất cơ bản của phân số
A. Bài tập Tính chất cơ bản của phân số
I. Bài tập trắc nghiệm
Câu 1: Khoanh vào chữ cái đặt trước kết quả đúng:
Phân số chỉ phần được tô màu trong hình vẽ là:
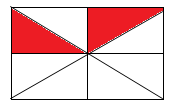
A.
B.
C.
D.
Câu 2: Số thích hợp được điền vào chỗ chấm là:
A. 389
B. 983
C. 938
D. 398
Câu 3: Phân số được đọc là:
A. Mười tám phần hai mươi năm
B. Hai mươi lăm phần mười tám
C. Hai lăm phần mười tám
D. Mười tám phần hai mươi lăm
Câu 4: Phép tính nào đúng tương ứng với phân số
A.
B.
C.
D.
Câu 5: Phân số biểu diễn số tự nhiên 2018 là:
A.
B.
C.
D.
Câu 6: Trong các đáp án sau, đáp án nào viết sai?
A.
B.
C.
D.
Câu 7: Chọn đáp án đúng trong các đáp án sau:
A.
B.
C.
D.
Câu 8: Phân số “Hai mươi chín phần bốn mươi hai” được viết là:
A.
B.
C.
D.
II. Bài tập tự luận
Câu 1:
a) Đọc các phân số sau :
: ………………………………………………………………………
: ………………………………………………………………………
: ………………………………………………………………………
b) Viết các phân số sau :
Bốn phần năm : …………………………………………………………
Ba mươi lăm phần bốn mươi tám : ……………………………………..
Bảy mươi tám phần hai trăm linh ba : ………………………………….
Câu 2: Viết số thích hợp vào chỗ chấm :
a)
b)
Câu 3: Quy đồng mẫu số các phân số sau:
a) và
b) và
c) và
d) và
Câu 4:
a) Viết các phân số sau theo thứ tự từ bé đến lớn : ; ;
b) Viết các phân số sau theo thứ tự từ lớn đến bé: ; ;
Câu 5: Chỉ ra các cặp phân số bằng nhau trong các phân số sau:
; ; ; ; ; ; ;
III. Bài tập vận dụng
Câu 1: Nêu tính chất cơ bản của phân số
Câu 2: Rút gọn các phân số sau:
Câu 3: Quy đồng mẫu số các phân số dưới đây:
Câu 4: Tìm các phân số bằng nhau trong các phân số dưới đây:
B. Lý thuyết Tính chất cơ bản của phân số
1. Tính chất cơ bản của phân số
– Nếu chia hết cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Ví dụ:
3. Ứng dụng tính chất cơ bản của phân số
Dạng 1: Rút gọn phân số
Bước 1: Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào lớn hơn 1
Bước 2: Chia cả tử số và mẫu số của phân số đó cho số vừa tìm được
Bước 3: Cứ làm thế cho đến khi tìm được phân số tối giản
Chú ý:
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số nào lớn hơn 1
Ví dụ:
Dạng 2: Quy đồng mẫu số các phân số
a) Trường hợp mẫu số chung bằng tích của hai mẫu số của hai phân số đã cho
Bước 1: Lấy cả tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai
Bước 2: Lấy cả tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất
Ví dụ: Quy đồng hai phân số và
MSC: 12
b) Mẫu số của một trong các phân số chia hết cho mẫu số của các phân số còn lại
Bước 1: Lấy mẫu số chung là mẫu số mà chia hết cho mẫu số của các phân số còn lại
Bước 2: Tìm thừa số phụ
Bước 3: Nhân cả tử số và mẫu số của các phân số còn lại với thừa số phụ tương ứng
Bước 4: Giữ nguyên phân số có mẫu số chia hết cho mẫu số của các phân số còn lại
Ví dụ: Quy đồng mẫu số hai phân số và .
MSC = 16