Câu hỏi:
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M. Đường thẳng vuông góc với OA tại O cắt MB tại C. Chứng minh CM = CO
Trả lời:
Sử dụng tính chất giao hai tiếp tuyến và OC//AM => => ΔOCM cân tại O
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Giải SGK Toán 7 Bài 3 (Cánh diều): Hai đường thẳng song song
Giải bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song
Giải Toán 7 trang 100 Tập 1
Câu hỏi khởi động trang 100 Toán lớp 7: Hình 33 minh họa góc quan sát của người phi công và góc quan sát của người hoa tiêu khi hướng dẫn máy bay bay vào vị trí ở sân bay
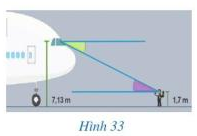
Theo em dự đoán, hai góc đó có bằng nhau hay không?
Phương pháp giải:
Ước lượng số đo 2 góc
Lời giải:
Dự đoán: góc quan sát của người phi công và góc quan sát của người hoa tiêu khi hướng dẫn máy bay vào vị trí sân bay bằng nhau.
I. Hai góc đồng vị. Hai góc so le trong
II. Dấu hiệu nhận biết hai đường thẳng song song
Giải Toán 7 trang 101 Tập 1
Hoạt động 2 trang 101 Toán lớp 7: Quan sát các Hình 38a, 38b, 38c và đoán xem các đường thẳng nào song song với nhau.
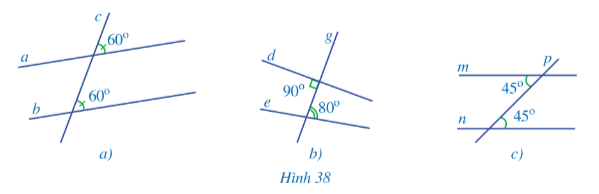
Lời giải:
– Hình 38a: Gọi giao điểm của đường thẳng a, b với đường thẳng c lần lượt là hai điểm A và B (như hình vẽ).
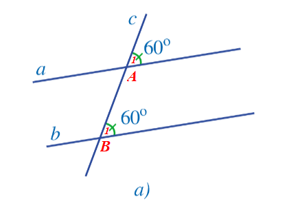
Nhận thấy: và và ở vị trí đồng vị.
Dự đoán: Đường thẳng a song song với đường thẳng b.
– Hình 38b: Gọi giao điểm của đường thẳng d, e với đường thẳng g lần lượt là hai điểm D và E (như hình vẽ).
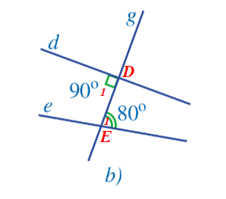
Nhận thấy: nên và và ở vị trí so le trong.
Dự đoán: Đường thẳng d không song song với đường thẳng e.
– Hình 38c: Gọi giao điểm của đường thẳng m, n với đường thẳng p lần lượt là hai điểm M và N (như hình vẽ).
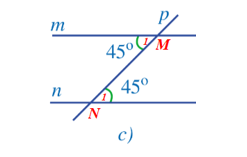
Nhận thấy: và và ở vị trí so le trong.
Dự đoán: Đường thẳng m song song với đường thẳng n.
Giải Toán 7 trang 102 Tập 1
Hoạt động 3 trang 102 Toán lớp 7: a) Thực hành vẽ đường thẳng b đi qua điểm M và song song với đường thẳng a ( M a) bằng ê ke theo các bước sau:
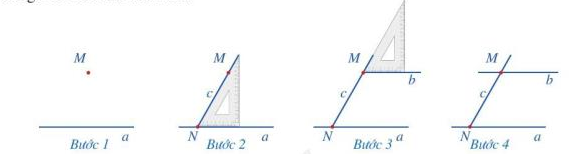
b) Giải thích vì sao đường thẳng b song song với đường thẳng a
Phương pháp giải:
Sử dụng dấu hiệu nhận biết 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
Lời giải:
a) Thực hiện vẽ hình theo các bước đã nêu ở đề bài.
b) Đường thẳng b song song với đường thẳng a vì đường thẳng c cắt 2 đường thẳng a và b tạo ra một cặp góc đồng vị bằng nhau
III. Tiên đề Euclid về đường thẳng song song
IV. Tính chất của hai đường thẳng song song
Giải Toán 7 trang 103 Tập 1
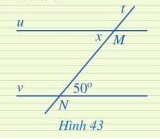
Luyện tập vận dụng trang 103 Toán lớp 7: Tìm số đo x trong Hình 43, biết u // v
Phương pháp giải:
Sử dụng tính chất: Đường thẳng c cắt 2 đường thẳng song song, tạo thành 1 cặp góc so le trong bằng nhau.
Lời giải:
Vì u // v nên x = 50 ( 2 góc so le trong)
Giải Toán 7 trang 104 Tập 1
Bài 1 trang 104 Toán lớp 7: Quan sát hình 44, biết a // b.
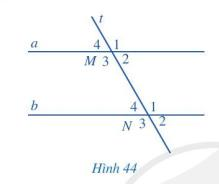
a) So sánh và ; và ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)
b) Tính: và ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
Phương pháp giải:
+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.
+ 2 góc đối đỉnh thì bằng nhau.
+ 2 góc kề bù có tổng số đo bằng 180
Lời giải:
a) Vì a // b nên ; ( 2 góc đồng vị) mà ; ( 2 góc đối đỉnh) nên =; =
b) Vì a // b nên ( 2 góc đồng vị), mà ( 2 góc kề bù) nên = 180; = 180
Chú ý:
Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau
+ Hai góc trong cùng phía có tổng số đo bằng 180
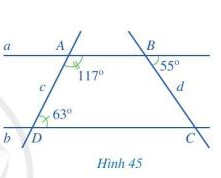
Bài 2 trang 104 Toán lớp 7: Quan sát Hình 45.
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tính số đo góc BCD.
Phương pháp giải:
+ Sử dụng tính chất: Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng tạo ra một cặp góc so le trong bằng nhau hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song
+ Sử dụng tính chất: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
Lời giải:
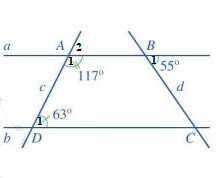
a) Vì ( 2 góc kề bù) nên
Vì ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
a // b ( đpcm)
b) Vì a // b nên ( 2 góc so le trong), mà
Bài 3 trang 104 Toán lớp 7: Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
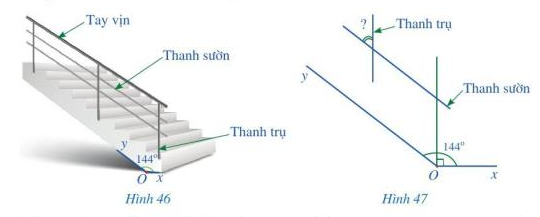
Trong Hình 46, góc xOy bằng 144. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?
Phương pháp giải:
Sử dụng tính chất: + Hai góc kề bù có tổng số đo bằng 180 độ
+ Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
Lời giải:
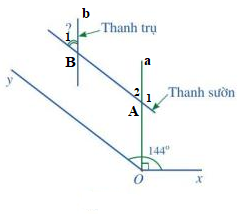
Vì AB // Oy nên ( 2 góc đồng vị), mà
Vì ( 2 góc kề bù) nên
Vì a // b nên ( 2 góc đồng vị), mà .
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 1: Góc ở vị trí đặc biệt
Bài 2: Tia phân giác của một góc
Bài 4: Định lí
Bài tập cuối chương 4
- 20 Bài tập Hai đường thẳng song song có đáp án – Toán 7
Bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song
A. Bài tập Hai đường thẳng song song
A.1 Bài tập tự luận
Bài 1. Cho hình vẽ sau:
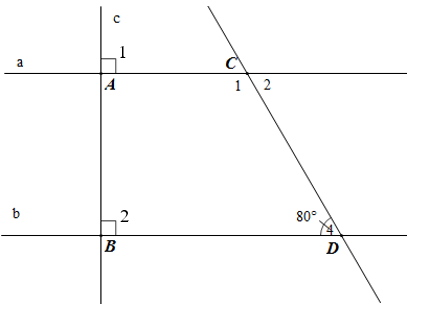 a) Vì sao a // b?
a) Vì sao a // b?b) Tính số đo các góc C1, C2 trong hình vẽ.
Hướng dẫn giải
a) Ta có góc A1 và góc B2 là hai góc ở vị trí đồng vị, mà .
Vậy nên a // b (dấu hiệu nhận biết hai đường thẳng song song).
b) Ta có góc C1 và D4 là hai góc trong cùng phía.
Mà a // b nên
Suy ra .
Góc C2 và góc D4 ở vị trí so le trong nên .
Vậy ; .
Bài 2. Cho hình vẽ
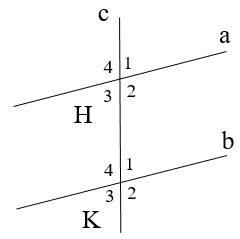
Biết Tính .
Hướng dẫn giải
Xét hai đường thẳng a và b cùng cắt đường thẳng c có: .
Mà hai góc này ở vị trí so le trong nên a // b
Suy ra (hai góc ở vị trí trong cùng phía)
Vậy .
A.2 Bài tập trắc nghiệm
Câu 1. Cho hình vẽ dưới đây:
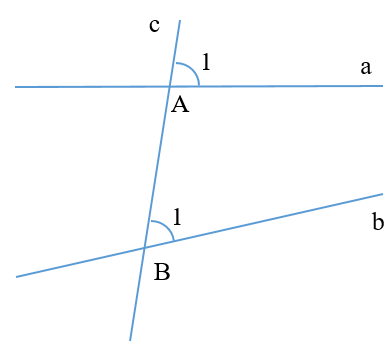
và là hai góc:
A. so le trong;
B. kề bù;
C. đồng vị;
D. kề nhau.
Hướng dẫn giải
Đáp án đúng là: C
và là hai góc đồng vị.
Câu 2. Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
A. Một cặp;
B. Hai căp;
C. không có cặp nào;
D. Vô số cặp.
Hướng dẫn giải
Đáp án đúng là: D
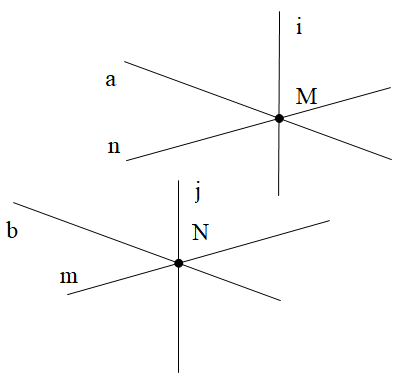 Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N và song song với đường thẳng đó (theo Tiên đề Euclid). Chẳng hạn, trên hình vẽ ta có b // a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Câu 3. Cho hình vẽ
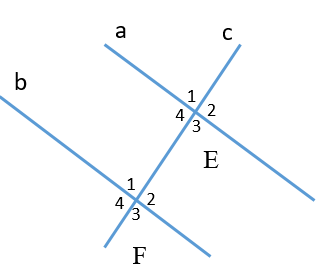
Biết a // b, . Số đo là:
A. 51°;
B. 129°;
C. 138°;
D. 48°.
Hướng dẫn giải
Đáp án đúng là: A
Ta có: và là hai góc đồng vị và a // b nên .
Mà ta lại có và là hai góc đối đỉnh nên .
Vậy
B. Lý thuyết Hai đường thẳng song song
1. Hai góc đồng vị. Hai góc so le trong

Đường thẳng c cắt hai đường thẳng a, b lần lượt tại điểm A, B.
Khi đó, ta thấy:
+ Góc A1 và góc B1 ở “cùng một phía” của đường thẳng c.
+ Góc A1 ở “phía trên” đường thẳng a. Góc B1 cũng ở “phía trên” đường thẳng b.
Hai góc A1 và B1 ở vị trí như thế được gọi là hai góc đồng vị.
 + Góc A3 và góc B1 ở “hai phía” của đường thẳng c.
+ Góc A3 và góc B1 ở “hai phía” của đường thẳng c.+ Góc A3 ở “phía dưới” của đường thẳng a. Góc B1 lại ở “phía trên” của đường thẳng b.
Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
Ví dụ: Kể tên các cặp góc so le trong và đồng vị trong hình sau:
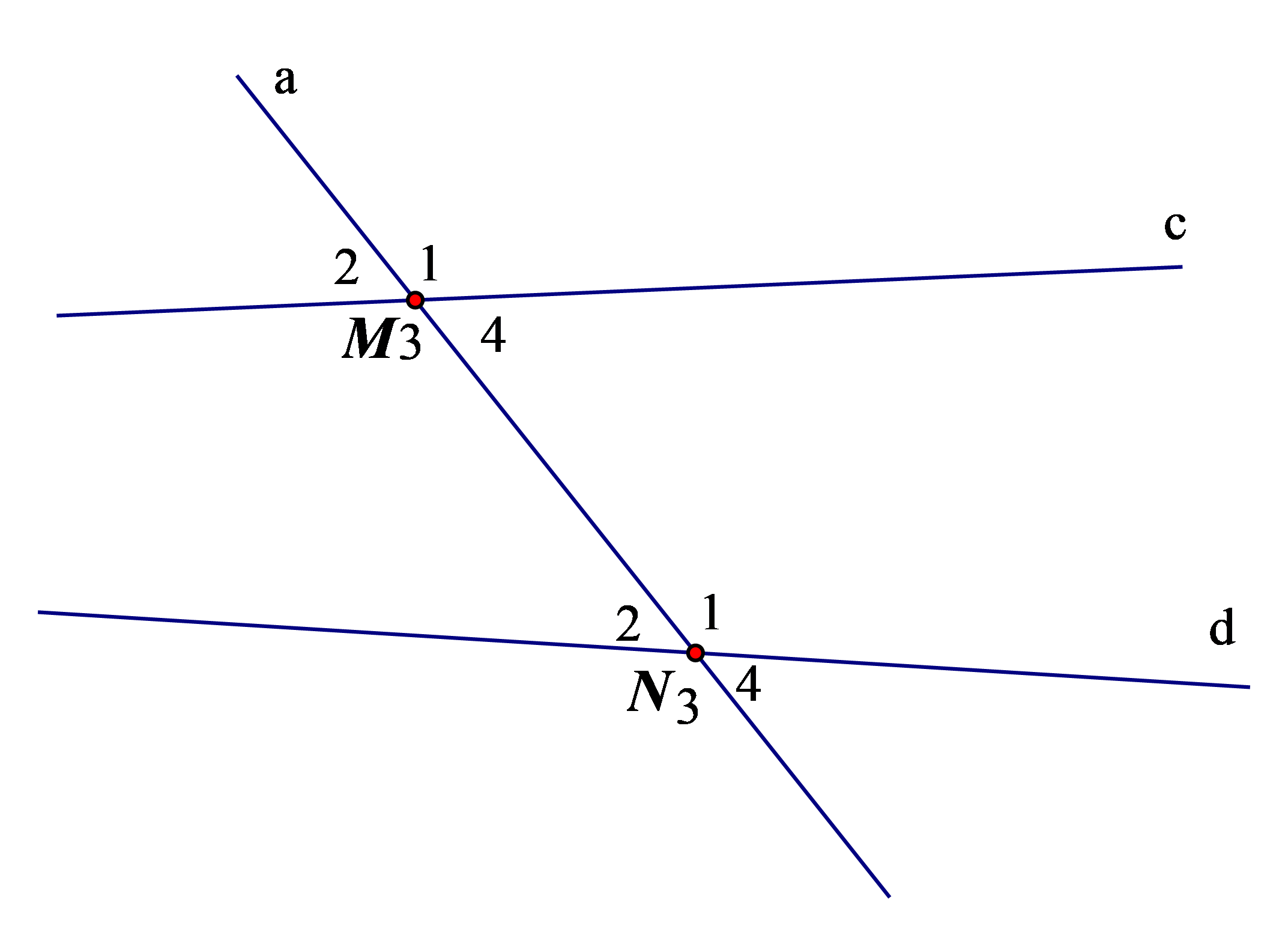 Hướng dẫn giải
Hướng dẫn giảiCác cặp góc so le trong là: M3 và N1; M4 và N2.
Các cặp góc đồng vị là: M1 và N1; M2 và N2; M3 và N3; M4 và N4.
2. Dấu hiệu nhận biết hai đường thẳng song song
– Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì a và b song song với nhau.
– Nếu đường thẳng c cắt hai đường thẳng a và b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì a và b song song với nhau.
Ví dụ:
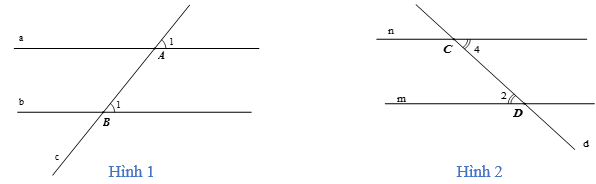
– Ở hình 1: Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau nên a // b.
– Ở hình 2: Đường thẳng d cắt hai đường thẳng m, n và trong các góc tạo thành có một cặp góc so le trong bằng nhau nên m // n.
Ví dụ: Vẽ một đường thẳng b đi qua điểm M và song song với đường thẳng a (M ∉ a) bằng êke.
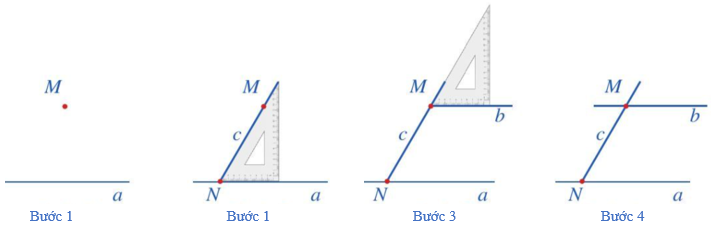 Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.
Bước 1: Vẽ đường thẳng a và điểm M không thuộc a.Bước 2: Đặt ê ke sao cho cạnh ngắn của góc vuông nằm trên đường thẳng a và cạnh huyền đi qua điểm M, vẽ theo cạnh huyền một phần đường thẳng c đi qua M (đường thẳng c cắt đường thẳng a tại điểm N).
Bước 3: Dịch chuyển ê ke sao cho cạnh huyền của ê ke vẫn nằm trên đường thẳng c còn cạnh ngắn của góc vuông đi qua điểm M, vẽ theo cạnh ngắn của góc vuông một phần đường thẳng b đi qua điểm M.
Bước 4: Vẽ hoàn thiện đường thẳng b.
Nhận xét: Qua một điểm ở ngoài một đường thẳng luôn có một đường thẳng song song với đường thẳng đó.
3. Tiên đề Euclid về đường thẳng song song
Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Nhận xét: Nếu hai đường thẳng cùng đi qua điểm M và cùng song song song với đường thẳng a (M ∉ a) thì hai đường thẳng đó trùng nhau.
Ví dụ:
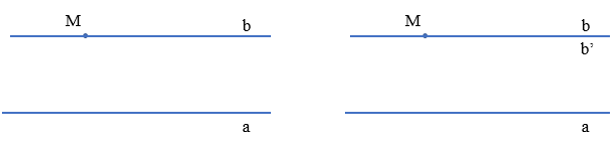 Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.
Qua điểm M nằm ngoài đường thẳng a ta vẽ được một đường thẳng b song song với a.Và vẽ được đường thẳng b’ cũng đi qua M và b’ song song với a.
Khi đó theo Tiên đề Euclid thì b và b’ trùng nhau.
4. Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
– Hai góc đồng vị bằng nhau.
– Hai góc so le trong bằng nhau.
Ví dụ: Tính số đo các góc A1 và góc D2 trong hai hình vẽ sau, biết a // b và m // n.
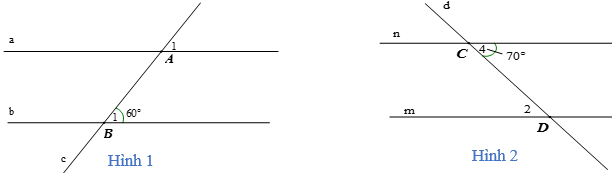
Hướng dẫn giải
– Hình 1: Do a // b nên ta có: (hai góc đồng vị), mà nên .
Vậy .
– Hình 2: Do m // n nên: (hai góc so le trong), mà nên .
Vậy .
Chú ý: Nếu đường thẳng c cắt hai đường thẳng song song a và b thì:
+ Hai góc so le ngoài bằng nhau.
+ Hai góc trong cùng phía có tổng số đo bằng 180°.
Ví dụ:
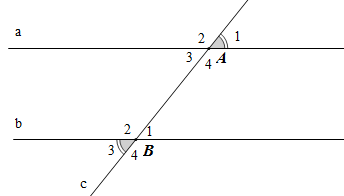
– Các cặp góc so le ngoài A1 và B3; A2 và B4; Khi đó: và .
– Hai góc trong cùng phía: góc A3 và góc B2; góc A4 và góc B1.
Khi đó: ; .
- Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai đường thẳng song song
Giải SBT Toán lớp 7 Bài 3: Hai đường thẳng song song
Giải trang 110 Tập 1
Bài 16 trang 110 Tập 1: Quan sát Hình 28, biết a // b,
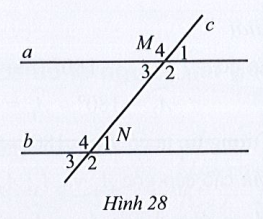
a) Nêu những cặp góc so le trong, những cặp góc đồng vị.
b) Tìm số đo mỗi góc còn lại của đỉnh M và N.
Lời giải:
a) Những cặp góc so le trong là: và và
Những cặp góc đồng vị là: và và và và
b)
– Tại đỉnh M:
• Vì và là hai góc đối đỉnh nên:
• Vì và là hai góc kề bù nên:
Suy ra
Vì và là hai góc đối đỉnh nên:
– Tại đỉnh N:
Vì a // b nên
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy
Bài 17 trang 110 Tập 1: Quan sát Hình 29, biết a // b, Tìm số đo mỗi góc của đỉnh A và B.
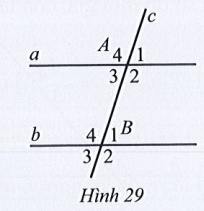
Lời giải:
– Tại đỉnh A:
• Ta có (hai góc kề bù).
Mà hay
Nên
Do đó
Suy ra
Khi đó
• (hai góc đối đỉnh).
• (hai góc đối đỉnh).
– Tại đỉnh B: Vì a // b nên ta có:
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy
Bài 18 trang 110 Tập 1: Tìm số đo mỗi góc B1, B2, B3, B4 trong Hình 30, biết m // n.
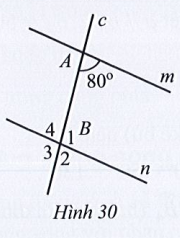
Lời giải:
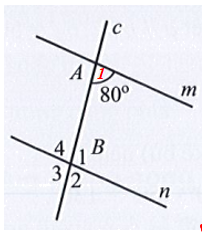
Giả sử như hình vẽ.
Vì m // n nên ta có:
• (hai góc so le trong);
• (hai góc đồng vị).
• (hai góc trong cùng phía)
Suy ra
Do đó (hai góc đối đỉnh).
Vậy
Bài 19 trang 110 Tập 1: Quan sát Hình 31, biết Tìm số đo mỗi góc còn lại của đỉnh M và N.
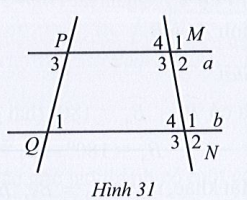
Lời giải:
+) Ta có: (hai góc đối đỉnh).
Vì và là hai góc kề bù nên ta có:
Suy ra
Do đó (hai góc đối đỉnh).
+) Ta có mà hai góc này ở vị trí so le trong
Nên PM // QN.
Do đó:
• (hai góc so le trong).
• (hai góc đồng vị).
• (hai góc đồng vị).
• (hai góc so le trong).
Vậy và
Bài 20 trang 110 Tập 1: Tìm số đo x, y trong Hình 32.
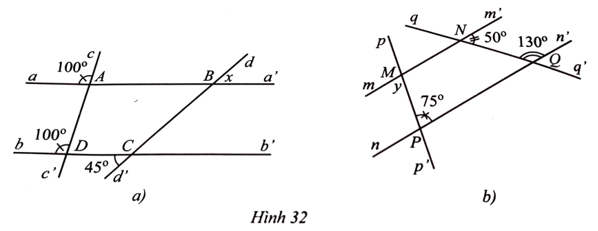
Lời giải:
a) Ta có (cùng bằng 100°).
Mà hai góc này ở vị trí đồng vị.
Do đó aa’ // bb’.
Suy ra (hai góc do le ngoài).
Vậy x = 45°.
b) Vì và là hai góc kề bù nên ta có:
Suy ra
Do đó (cùng bằng 50°).
Mà hai góc này ở vị trí so le trong nên mm’ // nn’.
Suy ra
Vậy y = 75°.
Giải trang 111 Tập 1
Bài 21 trang 111 Tập 1: Tìm số đo góc BCD trong Hình 33.
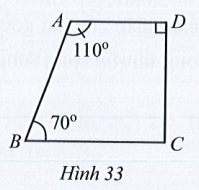
Lời giải:
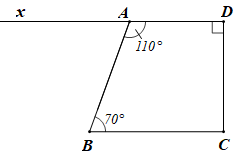
Vẽ tia Ax là tia đối của tia AD.
Khi đó và là hai góc kề bù nên ta có:
Suy ra
Do đó (cùng bằng 70°).
Mà hai góc này ở vị trí so le trong nên Dx // Cy.
Suy ra (hai góc trong cùng phía)
Do đó
Vậy
Bài 22 trang 111 Tập 1: Quan sát Hình 34, biết d1 // d2 và góc tù tạo bởi đường thẳng a và đường thẳng d1 bằng 150°. Tính góc nhọn tạo bởi đường thẳng a và đường thẳng d2.
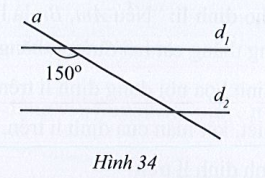
Lời giải:
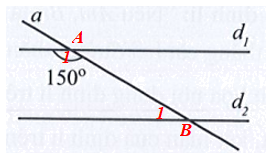
Giả sử là góc tù được tạo bởi đường thẳng a và đường thẳng d1;
là góc nhọn được tạo bởi đường thẳng a và đường thẳng d2.
Vì d1 // d2 nên (hai góc trong cùng phía).
Do đó
Vậy góc nhọn được tạo bởi đường thẳng a và đường thẳng d2 bằng 30°.
Bài 23 trang 111 Tập 1: Quan sát Hình 35, biết xx’ // yy’ // zz’. Chứng tỏ rằng
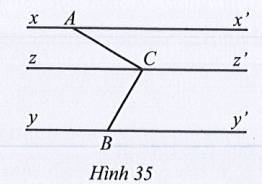
Lời giải:
Vì xx’ // zz’ nên (hai góc so le trong).
Vì yy’ // zz’ nên (hai góc so le trong).
Mặt khác: và là hai góc kề nhau
Nên
Do đó
Vậy
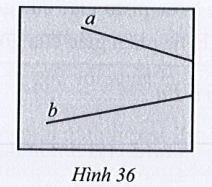
Bài 24* trang 111 Tập 1: Bạn Khôi vẽ hai đường thẳng a và b cắt nhau tại một điểm ở ngoài phạm vi tờ giấy (Hình 36). Em hãy giúp bạn Khôi nêu cách đo góc nhọn tạo bởi hai đường thẳng a và b đã vẽ.
Lời giải:
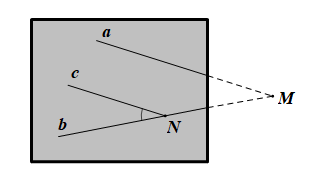
Giả sử đường thẳng a và đường thẳng b cắt nhau tại M nằm ngoài tờ giấy.
Khi đó góc nhọn tạo bởi hai đường thẳng a và b là
Trên đường thẳng b ta lấy điểm N, kẻ Nc // a sao cho là góc nhọn (hình vẽ).
Vì Nc // a nên (hai góc đồng vị).
Do đó ta đo góc bNc sẽ suy ra số đo của góc được tạo bởi hai đường thẳng a và b.
Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 2 : Tia phân giác của một góc
Bài 3 : Hai đường thẳng song song
Bài 4 : Định lí
Bài tập cuối chương 4
Bài 1 : Thu thập, phân loại và biểu diễn dữ liệu
- 20 câu Trắc nghiệm Hai đường thẳng song song (Cánh diều) có đáp án 2023 – Toán lớp 7
Trắc nghiệm Toán 7 Bài 3: Hai đường thẳng song song
Câu 1. Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
A. hai đường thẳng x, y song song với nhau;
B. hai đường thẳng x, y cắt nhau;
C. hai đường thẳng x, y trùng nhau;
D. hai đường thẳng x, y vuông góc với nhau.
Hướng dẫn giải
Đáp án đúng là: A
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì x, y song song với nhau.
Câu 2. Cho hình vẽ
Biết một cặp góc đồng vị . Tính số đo của cặp góc đồng vị và .
A. 130°;
B. 50°;
C. 60°;
D.150°.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
=> Chọn phương án D.
Câu 3. Biết một cặp góc so le trong . Tính số đo của cặp góc so le trong còn lại:
A. 144°;
B. 136°;
C. 66°;
D. 64°.
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
(hai góc kề bù)
Mà và ; và là hai cặp góc so le trong.
Do đó,
Vậy số đo của cặp góc so le trong còn lại là .
Câu 4. Cho hình vẽ
Biết Tính
A. 180°;
B. 138°;
C. 120°;
D. 148°.
Hướng dẫn giải
Đáp án đúng là: A
Xét hai đường thẳng a và b cùng cắt đường thẳng c có:
Mà hai góc này ở vị trí so le trong nên a // b
Suy ra (hai góc ở vị trí trong cùng phía)
Vậy
Câu 5. Cho hình vẽ
Biết a // b, . Tính số đo
A. 138°;
B. 142°;
C. 42°;
D. 158°.
Hướng dẫn giải
Đáp án đúng là: C
Vì a // b nên ( do và là hai góc đồng vị).
Suy ra .
Vậy .
Câu 6. Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
A. một đường thẳng;
B. hai đường thẳng;
C. không đường thẳng;
D. vô số đường thẳng.
Hướng dẫn giải
Đáp án đúng là: A
Theo tiên đề Euclid ta có: qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Câu 7. Nếu một đường thẳng cắt hai đường thẳng song song thì:
A. hai góc đồng vị bằng nhau;
B. hai góc kề nhau bằng nhau;
C. hai góc bù nhau bằng nhau;
D. hai góc kề bù bằng nhau.
Hướng dẫn giải
Đáp án đúng là: A
Nếu một đường thẳng cắt hai đường thẳng song song thì:
Hai góc đồng vị bằng nhau;
Hai góc so le trong bằng nhau.
Câu 8. Cho hình vẽ dưới đây:
và là hai góc:
A. so le trong;
B. kề bù;
C. đồng vị;
D. kề nhau.
Hướng dẫn giải
Đáp án đúng là: C
và là hai góc đồng vị.
Câu 9. Chọn phát biểu đúng.
A. và là hai góc so le trong
B. và là hai góc so le ngoài;
C. và là hai góc đồng vị;
D. và là hai góc đồng vị.
Hướng dẫn giải
Đáp án đúng là: D
và là hai góc so le trong là phát biểu sai, vì đó là hai góc đồng vị, loại phương án A;
và là hai góc so le ngoài là phát biểu sai, vì đó là hai góc đồng vị, loại phương án B;
và là hai góc đồng vị là phát biểu sai, vì đó là hai góc so le trong, loại phương án C;
và là hai góc đồng vị là phát biểu đúng, chọn phương án D.
Câu 10. Chọn một cặp góc đồng vị trong hình vẽ sau:
A. và ;
B. và ;
C. và ;
D. và .
Hướng dẫn giải
Đáp án đúng là: B
và là hai góc đồng vị là phát biểu sai, vì và là hai góc kề bù, loại phương án A.
và là hai góc đồng vị là phát biểu đúng, chọn phương án B.
và là hai góc đồng vị là phát biểu sai, vì và là hai góc so le trong, loại phương án C.
và là hai góc đồng vị là phát biểu sai, vì và là hai góc đối đỉnh, loại phương án D.
Câu 11. Chọn hình vẽ. Em hãy chọn câu trả lời đúng.
A. và là hai góc so le trong;
B. và là hai góc so le trong;
C. và là hai góc đồng vị;
D. và là hai góc đồng vị.
Hướng dẫn giải
Đáp án đúng là: B
và là hai góc so le trong là phát biểu sai, vì và là hai góc trong một tam giác loại phương án A.
và là hai góc so le trong là phát biểu đúng, chọn phương án B.
và là hai góc đồng vị là phát biểu sai.
và là hai góc đồng vị là phát biểu sai, vì và có đỉnh chung và có một cạnh chung nên là hai góc kề nhau, do đó loại phương án D.
Câu 12. Cho hình vẽ
Biết a // b, . Số đo là:
A. 51°;
B. 129°;
C. 138°;
D. 48°.
Hướng dẫn giải
Đáp án đúng là: A.
Ta có: và là hai góc đồng vị và a // b =>
Mà ta lại có và là hai góc đối đỉnh nên =>
Vậy
Câu 13. Trong các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
A. 0;
B. 1;
C. 2;
D. 3.
Hướng dẫn giải
Đáp án đúng là: C
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
Hai góc bù nhau là hai góc có tổng số đo bằng 180o
=> Có 2 câu đúng, chọn đáp án C.
Câu 14. Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
A. Một cặp;
B. Hai căp;
C. không có cặp nào;
D. Vô số cặp.
Hướng dẫn giải
Đáp án đúng là: D
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N (theo Tiên đề Euclid) và song song với đường thẳng đó. Trên hình vẽ ta có b //a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Câu 15. Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:
A. Hai đường thẳng đó trùng nhau;
B. Hai đường thẳng cắt nhau tại A;
C. Hai đường thẳng song song;
D. Hai đường thẳng vuông góc.
Hướng dẫn giải
Đáp án đúng là: A
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
Do đó, qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì hai đường thẳng đó phải trùng nhau.
=> Chọn đáp án A.
Xem thêm các bài trắc nghiệm Toán 7 Cánh diều hay, chi tiết khác:
Trắc nghiệm Toán 7 Bài 2: Tia phân giác của một góc
Trắc nghiệm Toán 7 Bài 3: Hai đường thẳng song song
Trắc nghiệm Toán 7 Bài 4: Định lí
Trắc nghiệm Ôn tập chương 4
Trắc nghiệm Toán 7 Bài 1: Thu thập, phân loại và biểu diễn dữ liệu
- Vở bài tập Toán 7 Bài 3: Hai đường thẳng song song – Cánh diều
Giải VBT Toán lớp 7 Bài 3: Hai đường thẳng song song
I. Kiến thức trọng tâm
Câu 1 trang 102 vở bài tập Toán lớp 7 Tập 1:
– Ở Hình 21, góc A1 và góc B1 ở …………………….. của đường thẳng c; góc A1 ở …………….. đường thẳng a, góc B1 cũng ở …………………. đường thẳng b. Hai góc A1 và B1 ở vị trí như thế gọi là……………………………
– Ở Hình 22, góc A3 và góc B1 ở ………………… của đường thẳng c; góc A3 ở ………………….. đường thẳng a, còn góc B1 lại ở …………. đường thẳng b. Hai góc A3 và B1 ở vị trí như thế gọi là …………………
– Nếu đường thẳng …….. cắt hai đường thẳng ………, …….. và trong các góc tạo thành có một cặp góc đồng vị ………………….thì hai đường thẳng ………, ……… song song với nhau.
– Nếu đường thẳng …….. cắt hai đường thẳng ………, ……… và trong các góc tạo thành có một cặp góc so le trong …………….. thì hai đường thẳng ………, ……… song song với nhau.
– Tiên đề Euclid về đường thẳng song song: Qua một điểm ở ngoài một đường thẳng chỉ có ………………………………….. song song với đường thẳng đó.
– Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị ……………………………………………………………………………………
– Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong
……………………………………………………………………………………
Lời giải:
– Ở Hình 21, góc A1 và góc B1 ở cùng một phía của đường thẳng c; góc A1 ở phía trên đường thẳng a, góc B1 cũng ở phía trên đường thẳng b. Hai góc A1 và B1 ở vị trí như thế gọi là hai góc đồng vị.
– Ở Hình 22, góc A3 và góc B1 ở hai phía của đường thẳng c; góc A3 ở phía dưới đường thẳng a, còn góc B1 lại ở phía trên đường thẳng b. Hai góc A3 và B1 ở vị trí như thế gọi là hai góc so le trong.
– Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng a, b song song với nhau.
– Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau.
– Tiên đề Euclid về đường thẳng song song: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
– Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
– Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
II. Luyện tập
Câu 1 trang 103 vở bài tập Toán lớp 7 Tập 1: Quan sát từng hình và viết vào chỗ chấm (…) ở bảng sau cho thích hợp:
Lời giải:
Câu 2 trang 104 vở bài tập Toán lớp 7 Tập 1: Quan sát Hình 25, biết a // b.
a) So sánh và ; và (mỗi cặp và , và gọi là một cặp góc so le ngoài).
b) Tính và (mỗi cặp và , và gọi là một cặp góc trong cùng phía).
Lời giải:
a) Do a // b nên = (hai góc đồng vị).
Mặt khác (hai góc đối đỉnh). Suy ra: = .
Do a // b nên = (hai góc đồng vị).
Mặt khác = (hai góc đối đỉnh). Suy ra: =
b) Ta có: = 180° (hai góc kề bù)
Lại có a // b nên (hai góc đồng vị). Suy ra: = 180°.
Tương tự, ta có: (hai góc kề bù)
Lại có a // b nên (hai góc đồng vị). Suy ra: = 180°.
Câu 3 trang 104 vở bài tập Toán lớp 7 Tập 1: Quan sát Hình 26.
a) Vì sao hai đường thẳng a và b song song với nhau ?
b) Tính số đo góc BCD.
Lời giải:
a) Do = 180° (hai góc kề bù) nên . Do đó, (cùng bằng 63°).
Do và là hai góc đồng vị nên a // b.
b) Từ kết quả câu a suy ra (hai góc so le trong). Từ đó, .
Câu 4 trang 104 vở bài tập Toán lớp 7 Tập 1: Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
Trong Hình 27, góc xOy bằng 144°. Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ ? (Xem hướng dẫn ở Hình 28).
Lời giải:
Ta có góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can bằng góc mAn.
Do An // Bz nên (hai góc đồng vị). Do AB // Oy nên (hai góc đồng vị). Từ đó, ta có: .
Ta có (hai góc kề nhau) và suy ra hay .
III. Bài tập
Câu 1 trang 105 vở bài tập Toán lớp 7 Tập 1: Tìm các số đo x và y trong Hình 29, biết m // n.
Lời giải:
– Do m // n nên x = 47° (hai góc so le trong)
– Mặt khác, ta có x + y = 180° (hai góc kề bù).
Suy ra: y = 180° – x = 180° – 47° = 133°.
Câu 2 trang 105 vở bài tập Toán lớp 7 Tập 1: Bạn Hải cho rằng: Khi điểm M không thuộc đường thẳng c, nếu hai đường thẳng a, b cùng đi qua M và cùng song song với c thì a và b trùng nhau. Bạn Hải nói đúng hay sai, vì sao ?
Lời giải:
Theo tiên đề Euclid thì qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Như thế, qua điểm M không thuộc đường thẳng c chỉ có một đường thẳng song song với đường thẳng c, tức là nếu hai đường thẳng a, b cùng đi qua M và cùng song song với c thì a và b trùng nhau. Vậy bạn Hải nói đúng.
Câu 3 trang 106 vở bài tập Toán lớp 7 Tập 1: Ở Hình 30 có AB // CD, , . Tính số đo các góc:
a) ;
b) .
Lời giải:
a) Do AB // CD nên (hai góc đồng vị).
Mà = 90° suy ra .
b) Do AB // CD nên (hai góc đồng vị)
Mà suy ra .
Lại có (hai góc kề bù). Từ đó, suy ra .