Giải SBT Toán lớp 6 Bài 5: Phép nhân các số nguyên
Bài 40 trang 81 sách bài tập Toán lớp 6 Tập 1: Thực hiện phép tính:
a) (-6).9; b) (-12).(-987);
c) 90.(-108).(-3); d) 29.(-78).(-9).(-11);
e) 6.(-4)2.(-10)2 + 52; f) (-7).(-7).(-7) + 73;
h) (-103).(-102) – 132; i) (-8).(-8).(-8).(-8) – 84 + 105.
Lời giải:
a) (-6).9
= -6.9
= -54.
b) (-12).(-987)
= 12.987
= 11 844.
c) 90.(-108).(-3)
= (-9 720).(-3)
= 29 160.
d) 29.(-78).(-9).(-11)
= (-2 262).(-9).(-11)
= 20 358.(-11)
= – 223 938.
e) 6.(-4)2.(-10)2 + 52
= 6.16.100 + 25
= 9 600 + 25
= 9 625.
f) (-7).(-7).(-7) + 73
= – 73 + 73
= 73 – 73
= 0.
h) (-103).(-102) – 132
= (-1 000).(-100) – 169
= 100 000 – 169
= 99 831.
i) (-8).(-8).(-8).(-8) – 84 + 105
= 84 – 84 + 105
= 0 + 105
= 105.
Bài 41 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn các dấu “+”, “-“ thích hợp cho  :
:
|
a |
b |
Dấu của a.b |
|
+ |
– |
? |
|
– |
+ |
? |
|
– |
– |
? |
|
+ |
+ |
? |
Lời giải:
+) a mang dấu dương, b mang dấu âm suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.
+) a mang dấu âm, b mang dấu dương suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.
+) a mang dấu âm, b mang dấu âm suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.
+) a mang dấu dương, b mang dấu dương suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.
Khi đó ta có bảng sau:
|
a |
b |
Dấu của a.b |
|
+ |
– |
– |
|
– |
+ |
– |
|
– |
– |
+ |
|
+ |
+ |
+ |
Bài 42 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn số thích hợp cho  :
:
|
a |
-23 |
221 |
? |
-25 |
12 |
|
b |
-9 |
-45 |
399 |
? |
? |
|
c |
2 |
? |
0 |
-1 |
-38 |
|
a.b |
? |
? |
1 197 |
-100 |
-156 |
|
c(a + b) |
? |
176 |
? |
? |
? |
Lời giải:
+) Với a = -23, b = -9, c = 2 thì:
a.b = (-23).(-9) = 207;
c(a + b) = 2.[(-23) + (-9)] = 2.(-32) = -64.
+) Với a = 221, b = -45, c(a + b) = 176 thì:
a.b = 221.(-45) = -9 945;
Ta có: c(a + b) = 176
c.[221 + (-45)] = 176
c.176 = 176
c = 1.
+) Với b = 399, c = 0, a.b = 1 197. Khi đó:
Ta có: a.b = 1 197
a.399 = 1 197
a = 1 197:399
a = 3;
c.(a + b) = 0.(399 + 3) = 0.402 = 0.
+) Với a = -25, c = -1 và a.b = -100. Khi đó:
Ta có: a.b = -100
(-25).b = -100
(-25).b = (-25).4
b = 4.
c(a + b) = (-1).[(-25) + 4] = (-1).(-21) = 21.
+) Với a = 12, c = -38, a.b = -156. Khi đó:
Ta có: a.b = -156
12.b = -156
12.b = 12.(-13)
b = -13;
c(a + b) = (-38).[12 + (-13)] = (-38).(-1) = 38.
Từ đó, ta có bảng sau:
|
a |
-23 |
221 |
3 |
-25 |
12 |
|
b |
-9 |
-45 |
399 |
4 |
-13 |
|
c |
2 |
1 |
0 |
-1 |
-38 |
|
a.b |
207 |
-9 945 |
1 197 |
-100 |
-156 |
|
c(a + b) |
-64 |
176 |
0 |
21 |
38 |
Bài 43 trang 82 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) 19x với x = – 7;
b) 28xy với x = -12 và y = -15;
c) 29m – 58n với m = -2 và n = 3;
d) (- 2021)abc + ab với a = -21, b = -11 và c = 0.
Lời giải:
a) Thay x = -7 vào 19x, ta được:
19.(-7) = -133.
Vậy với x = -7 thì giá trị biểu thức là -133.
b) Thay x = -12 và y = -15 vào biểu thức 28xy, ta được:
28.(-12).(-15) = (-336).(-15) = 5 040.
Vậy với x = -12 và y = -15 thì giá trị biểu thức là 5 040.
c) Thay m = -2 và n = 3 vào 29m – 58n, ta được:
29.(-2) – 58.3
= (-58) – 58.3
= (-58) + (-58).3
= (-58).(1 + 3)
= (-58).4
= -232.
Vậy với m = -2 và n = 3 thì giá trị biểu thức là -232.
d) Thay a = -21, b = -11 và c = 0 vào biểu thức (- 2021)abc + ab, ta được:
(- 2021)(-21).(-11).0 + (-21).(-11)
= 0 + 231
= 231.
Vậy với a = -21, b = -11 và c = 0 thì giá trị biểu thức là 231.
Bài 44 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn dấu “<”, “>”, “=” thích hợp cho dấu  :
:
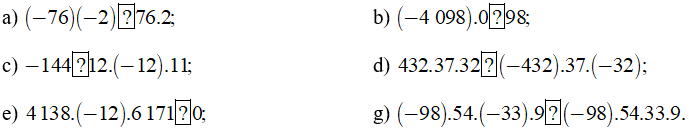
Lời giải:
a) Ta có (-76).(-2) = 76.2. Do đó ta điền: (-76)(-2) 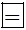 76.2
76.2
b) Ta có (-4 098).0 = 0 < 98. Do đó ta điền: (-4 098) : 0  98
98
c) Ta có 12.(-12).11 = (-144).11 = -1 584 < -144. Do đó ta điền: -144  12.(-12).11
12.(-12).11
d) Ta có: (-432).37.(-32) =-(432.37).(-32) = 432.37.32. Do đó ta điền: 432.37.32 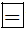 (-432).37.(-32)
(-432).37.(-32)
e) 4 138.(-12).6 171 = -(4 138.12).6 171 = -(4 138.12.6 171) < 0. Do đó ta điền: 4138.(-12).6171  0
0
g) Ta có: (-98).54.(-33).9 = 98.54.33.9, (-98).54.33.9 = -(98.54.33.9).
Vì -(98.54.33.9) < 98.54.33.9 nên (-98).54.33.9 < (-98).54.(-33).9. Do đó ta điền: (-98).54.(-33).9  (-98).54.33.9
(-98).54.33.9
Bài 45 trang 82 sách bài tập Toán lớp 6 Tập 1: Tính một cách hợp lí:
a) (-16).(-9).5;
b) (-15).999;
c) (-25).144.(-4);
d) (-125).2 020.(-8);
e) (-2 021).(-15) + (-15).2 020;
g) 121.(-63) + 63.(-53) – 63.26.
Lời giải:
a) (-16).(-9).5
= [(-16).5].(-9)
= (-80).(-9)
= 720.
b) (-15).999
= (-15)(1 000 – 1)
= (-15).1 000 – (-15).1
= -15 000 + 15
= -(15 000 – 15)
= -14 985.
c) (-25).144.(-4)
= [(-25).(-4)].144
= 100.144
= 14 400.
d) (-125).2 020.(-8)
= [(-125).(-8)].2 020
= 1 000.2 020
= 2 020 000.
e) (-2 021).(-15) + (-15).2 020
= (-15).[(-2 021) + 2 020]
= (-15).(-1)
= 15.
g) 121.(-63) + 63.(-53) – 63.26
= 121.(-63) + (-63).53 + (-63).26
= (-63).(121 + 53 + 26)
= (-63).200
= -12 600.
Bài 46 trang 83 sách bài tập Toán lớp 6 Tập 1: Báo cáo kinh doanh trong 6 tháng đầu năm của công ty Bình An được thống kê như sau:
|
Tháng |
Lợi nhuận (triệu đồng) |
|
Tháng 1 |
50 |
|
Tháng 2 |
-10 |
|
Tháng 3 |
50 |
|
Tháng 4 |
40 |
|
Tháng 5 |
-20 |
|
Tháng 6 |
-10 |
Sau 6 tháng đầu năm, công ty Bình An kinh doanh lãi hay lỗ với số tiền là bao nhiêu?
Lời giải:
Số tiền của công ty Bình An thu được sau 6 tháng đầu năm là:
50 + (-10) + 50 + 40 + (-20) + (-10) = 100 (triệu đồng)
Vậy sau 6 tháng đầu năm, công tu Bình An kinh doanh lãi 100 triệu đồng.
Bài 47 trang 83 sách bài tập Toán lớp 6 Tập 1: So sánh hai biểu thức sau mà không tính cụ thể giá trị của chúng:
a) (- 2021).2 021 và (-2 020).2 022;
b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.
Lời giải:
a) Ta có: (- 2021).2 021
= [(-2 020) + (-1)].2 021
= (-2 020).2 021 + (-1).2 021
= (-2 020).2 021 + (-2 021)
Ta có: (-2 020).2 022 = (-2 020)(2 021 + 1) = (-2 020).2 021 + (-2 020).
Vì -2 021 < -2 020 nên (-2 020).2 021 + (-2 021) < (-2 020).2 021 + (-2 020) hay (- 2021).2 021 < (-2 020).2 022.
b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.
Ta có 8 765 – 5 678 > 0, 5 678 – 9 765 + (-12) < 0.
Do đó (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 0 mà 4 342 > 0.
Vậy (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 4 342.
Bài 48 trang 83 sách bài tập Toán lớp 6 Tập 1: Cho hai số nguyên x, y (x ≠ 0, y ≠ 0, x > y, x ≠ -y)
Gọi m = x2.y2.(x – y).(x + y)4. Hỏi m là số nguyên dương hay nguyên âm?
Lời giải:
Vì x > y nên x – y > 0.
Ta có x2 ≥ 0 với mọi x mà x ≠ 0 nên x2 > 0.
Ta có y2 ≥ 0 với mọi x mà y ≠ 0 nên y2 > 0.
Ta lại có x ≠ – y nên x + y ≠ 0 suy ra (x + y)4 > 0.
Do đó m = x2.y2.(x – y).(x + y)4 > 0.
Vậy m là một số nguyên dương.
Bài 49 trang 83 sách bài tập Toán lớp 6 Tập 1: Tìm các số nguyên x thỏa mãn:
a) 16x2 = 64; b) 25(x2 – 1) – 75 = 9 900;
c) (x – 6).(2x – 6) = 0; d) (5x – 10)(6x + 12) = 0.
Lời giải:
a) 16x2 = 64
x2 = 64:16
x2 = 4
x2 = 22 = (-2)2
x = 2 hoặc x = -2.
Vậy x = 2 hoặc x = -2.
b) 25(x2 – 1) – 75 = 9 900
25(x2 – 1) = 9 900 + 75
25(x2 – 1) = 9 975
x2 – 1 = 9 975:25
x2 – 1 = 9 975:25
x2 – 1 = 399
x2 = 400
x2 = 202 = (-20)2
x = 20 hoặc x = -20.
Vậy x = 20 hoặc x = -20.
c) (x – 6).(2x – 6) = 0
TH1: x – 6 = 0
x = 6.
TH2: 2x – 6 = 0
2x = 6
x = 3.
Vậy x = 6 hoặc x = 3.
d) (5x – 10)(6x + 12) = 0
TH1: 5x – 10 = 0
5x = 10
x = 2.
TH2: 6x + 12 = 0
6x = -12
6x = 6.(-2)
x = -2.
Vậy x = 2 hoặc x = -2.
Bài 50 trang 83 sách bài tập Toán lớp 6 Tập 1: Cho bảng gồm 2 015×2 015 ô vuông nhỏ (Hình 9).
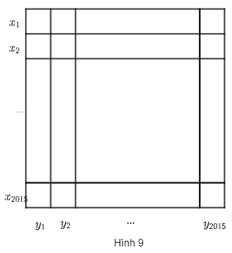
Điền vào mỗi ô của bảng số 1 hoặc số -1.
Bên trái mỗi dòng thứ i ghi tích các số của dòng đó và đặt là xi. Dưới mỗi cột thứ j ghi tích các số của cột đó và đặt là yj. (i = 1; 2; 3; …; 2 015 và j = 1; 2; 3; …; 2 015).
Chứng tỏ rằng tổng của 4 030 số xi,yj nhận được khác 0.
Lời giải:
Giả sử tổng của 4 030 số xi,yj bằng 0.
Ta có x1 + x2 + … + x2015 + y1 + y2 + … + y2015 = 0.
Mà mỗi số xi, yi đều bằng 1 hoặc -1 nên trong 4 030 số xi, yi có 2 015 số bằng -1 và 2 015 số bằng 1.
Do đó tích x1.x2…x2015.y1.y2…y2015 = – 1 (vì số các thừa số bằng -1 là lẻ). (1)
Mặt khác x1.x2…x2015 = y1.y2…y2015 (đều là tích của các số trong bảng).
Suy ra x1.x2…x2015.y1.y2…y2015 = (x1.x2…x2015)2 = 1. (mâu thuẫn với (1)).
Do đó giải sử sai.
Vậy tổng của 4 030 số xi,yj nhận được khác 0.