Giải SBT Toán lớp 6 Bài 3: Hình bình hành
Bài 19 trang 110 sách bài tập Toán lớp 6 Tập 1: Cho hình bình hành ABCD có AB = 12cm, BC = 8cm, AH = 6cm (AH là đường cao ứng với cạnh CD). Tính chu vi và diện tích của hình bình hành ABCD.
Lời giải:
Chu vi hình bình hành ABCD là: 2.(12 + 8) = 2.20 = 40 (cm).
Diện tích hình bình hành ABCD là: 12.6 = 72 (cm2).
Vậy chu vi hình bình hành là 40cm và diện tích hình bình hành là 72cm2.
Bài 20 trang 110 sách bài tập Toán lớp 6 Tập 1: Cho ba hình thoi như nhau, mỗi hình có chu vi 200cm, hai đường chéo có độ dài 60cm và 80cm. Tính chu vi và chiều cao của hình bình hành ghép bởi ba hình thoi đó (Hình 20).
Lời giải:
Cạnh của hình thoi là: 200:4 = 50 (cm).
Độ dài một cạnh của hình bình hành là: 50 + 50 + 50 = 150cm và cạnh còn lại là 50cm.
Khi đó, chu vi hình bình hành là: (150 + 50).2 = 200.2 = 400 (cm).
Diện tích một hình thoi là: (60.80):2 = 2 400 (cm2).
Vì một hình bình hành được ghép bởi ba hình thoi nên diện tích hình bình hành là:
3.2 400 = 7 200 (cm2).
Hình 20 a): Cạnh đáy tương ứng với đường cao AH là CD có độ dài 150 cm.
Đường cao của AH của hình bình hành ABCD là: 7 200:150 = 48 cm.
Hình 20 b): Cạnh đáy tương ứng với đường cao NK là QP có độ dài là 20cm.
Đường cao NK của hình bình hành MNPQ là: 7 200:50 = 144 cm.
Bài 21 trang 110 sách bài tập Toán lớp 6 Tập 1: Hai hình vuông ABCD và BEGC như nhau ghép thành hình chữ nhật AEGD. Nối B với D, E với C ta được hình bình hành BECD (Hình 21). Hãy tính diện tích hình bình hành đó, biết chu vi của hình chữ nhật AEGD là 216cm.
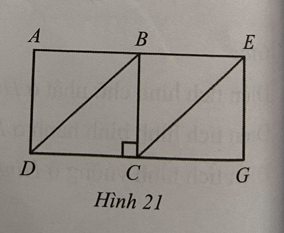
Lời giải:
Vì hình chữ nhật AEGD được ghép từ hai hình vuông ABCD và BEGC theo hình 21 nên chiều dài gấp đôi chiều rộng. Do đó chiều rộng của hình chữ nhật AEGD là:
(216: 2):3 = 36 (cm).
Do đó hình bình hành AEGD có cạnh đáy CD = 36cm và chiều cao BC = 36cm.
Diện tích hình bình hành AEGD là: 36.36 = 1 296 (cm2).
Vậy diện tích hình bình hành AEGD là 1 296 cm2.
Bài 22 trang 111 sách bài tập Toán lớp 6 Tập 1: Quan sát các hình bình hành ABCD, MBCN ở Hình 22. Tính diện tích hình bình hành ABCD, biết rằng diện tích hình bình hành MBCN là 8 cm2 và AB = 3MB.
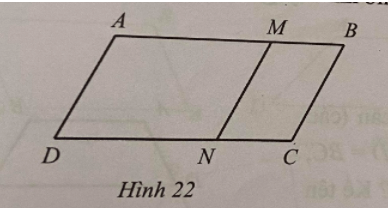
Lời giải:
Hai hình bình hành ABCD và MBCN có cùng chung đường cao ứng với đáy CD và NC.
Mà CD = 3NC ( do AB = 3MB)
Nên diện tích của hình bình hành ABCD gấp 3 lần diện tích hình bình hành MBCN và bằng: 3.8 = 24 (cm2).
Vậy diện tích hình bình hành ABCD là: 24 cm2.
Bài 23 trang 111 sách bài tập Toán lớp 6 Tập 1: Hãy cắt và ghép hình bình hành ở Hình 23 để được một hình chữ nhật.
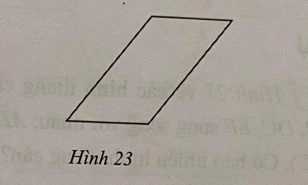
Lời giải:
Học sinh có thể thực hiện theo cách sau:
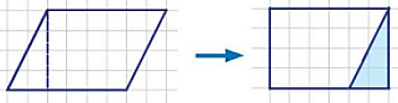
Bài 24 trang 111 sách bài tập Toán lớp 6 Tập 1: Quan sát hình chữ nhật ABCD và hình bình hành ABEG ở Hình 24. Biết hình chữ nhật ABCD có chu vi là 120cm và chiều dài hơn chiều rộng 10cm. Tính diện tích hình bình hành ABEG.
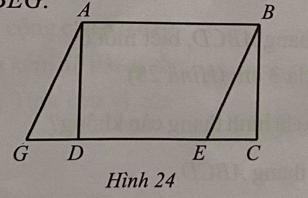
Lời giải:
Chiều rộng của hình chữ nhật là: (120:2 – 10):2 = 25 (cm).
Chiều dài của hình chữ nhật là: 25 + 10 = 35 (cm).
Hình bình hành ABEG có chiều cao bằng chiều rộng của hình chữ nhật ABEG và cạnh ứng với đường cao bằng với chiều dài của hình chữ nhật ABEG. Do đó diện tích hình bình hành ABEG là: 35.25 = 875 (cm2).
Vậy diện tích hình bình hành ABEG là 875 cm2.
Bài 25 trang 111 sách bài tập Toán lớp 6 Tập 1: Bạn An có một mảnh đất dạng hình chữ nhật kích thước 50m x 30m. Bác dự định làm một con đường ngang qua (phần tô đậm) có kích thước như trong Hình 25. Hãy giúp bác An tiết kiệm diện tích con đường và phần đường còn lại của mảnh đất.
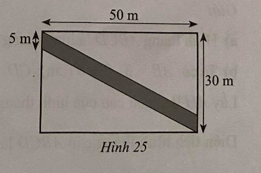
Lời giải:
Diện tích của mảnh đất hình chữ nhật là: 50.30 = 1 500 (m2).
Diện tích của con đường ngang qua mảnh đất là: 5.50 = 250 (m2).
Diện tích phần còn lại của mảnh đấy là: 1500 – 250 = 1 250 (m2).
Diện tích của con đường ngang qua mảnh đất là: 250 m2 và diện tích phần còn lại của mảnh đất là 1 250m2.