Lý thuyết Toán lớp 6 Chương 8: Những hình học cơ bản
Video giải Toán 6 Bài tập ôn cuối chương 8 trang 67 – Kết nối tri thức
I. Lý thuyết Toán lớp 6 Chương 8: Những hình học cơ bản
1. Điểm thuộc, không thuộc đường thẳng
a) Điểm, đường thẳng
– Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm
– Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.
– Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.
b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
– Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.
– Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.
– Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.
c) Đường thẳng đi qua hai điểm phân biệt
– Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt
2. Ba điểm thẳng hàng
– Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.
3. Hai đường thẳng song song, cắt nhau, trùng nhau.
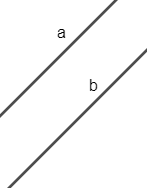
– Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.
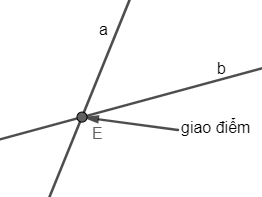
– Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.
– Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.
|
|
|
|
|
a và b song song với nhau kí hiệu: a // b |
a và b cắt nhau tại điểm E |
Đường thẳng AB và đường thẳng BC trùng nhau. |
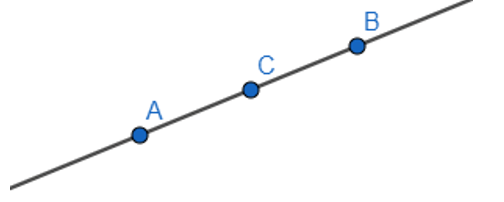
4. Điểm nằm giữa hai điểm

+ Điểm B nằm giữa hai điểm A và C.
+ Hai điểm A và B nằm cùng phía đối với điểm C.
+ Hai điểm A và C nằm khác phía đối với điểm B.
5. Tia
a) Tia
Điểm O trên đường thẳng xy chia đường thẳng xy thành hai phần.
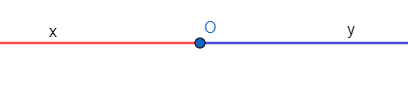
– Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O. Điểm O là gốc của tia.
b) Hai tia đối nhau
– Hai tia đối nhau là hai tia chung gốc và tạo thành một đường thẳng
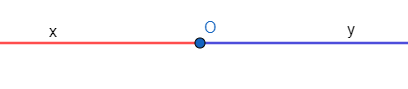
– Hai tia Ox và Oy là gọi là hai tia đối nhau (tia Ox là tia đối của tia Oy và tia Oy là tia đối của tia Ox).
c) Hai tia trùng nhau
– Hai tia trùng nhau là hai tia chung gốc và có thêm ít nhất 1 điểm chung khác điểm gốc
– Khi điểm B thuộc tia Am thì tia Am còn được gọi là tia AB, khi đó tia Am và tia AB được gọi là trùng nhau.

6. Đoạn thẳng
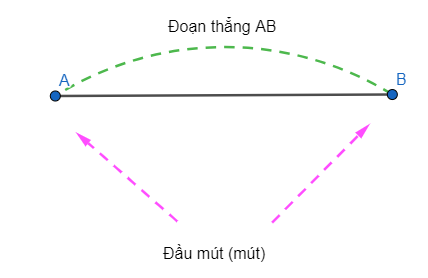
– Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.
– A; B là hai đầu mút (mút) của đoạn thẳng AB.
7. Độ dài đoạn thẳng
a) Độ dài đoạn thẳng
– Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).
– Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).
– Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…
b) So sánh độ dài đoạn thẳng
– Hai đoạn thẳng AB và EG có cùng độ dài. Ta viết AB = EG và nói đoạn thẳng AB bằng đoạn thẳng EG.

– Đoạn thẳng AB có độ dài nhỏ nhơn đoạn thẳng CD. Ta viết AB < CD và nói AB ngắn hơn CD hoặc CD > AB và nói CD dài hơn AB.

c) Đo độ dài đoạn thẳng
Để đo độ dài đoạn thẳng ta làm như sau:
Bước 1: Đặt thước trùng với đường thẳng sao cho vạch 0 của thước trùng với một đầu mút của đoạn thẳng.
Bước 2: Quan sát xem đầu mút còn lại trùng với vạch mấy của thước thì số chỉ ở vạch đó chính là độ dài đoạn thẳng.
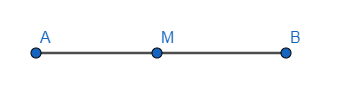
Chú ý: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB
8. Trung điểm của đoạn thẳng
– Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.
Khi đó:
IA = IB = 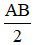 .
.

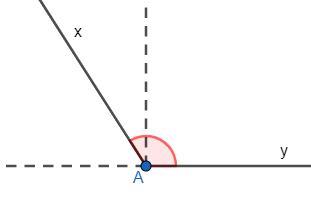
9. Góc
– Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.
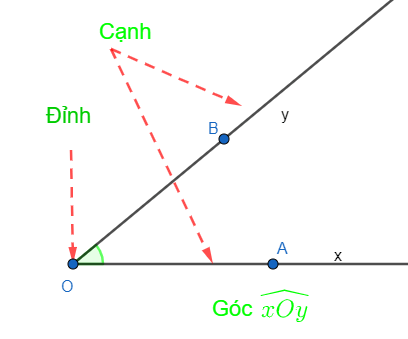
+ Góc xOy, kí hiệu 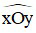 (hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.
(hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.
+ Điểm O là đỉnh của góc xOy. Hai tia Ox; Oy là các cạnh của góc xOy.
+ Góc xOy còn có các cách gọi khác là góc AOB; góc O; góc yOx; góc BOA.
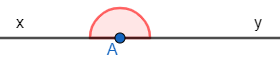
+ Đặt biệt khi Ox và Oy là hai tia đối nhau, ta có góc bẹt xOy.
10. Điểm trong của góc
Quan sát hình vẽ:
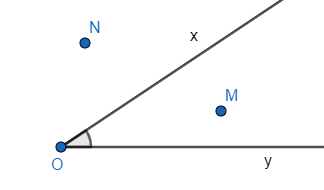
– Ta gọi M là một điểm trong của góc xOy (điểm M nằm trong góc xOy).
– Các điểm nằm trên hai cạnh của góc và các điểm như điểm N không phải là điểm trong góc xOy.
11. Đo góc
– Muốn đo 1 góc xOy, ta đặt thước đo góc sao cho tâm của thước trùng với O, tia Ox đi qua vạch 0. Khi đó tia Oy đi qua vạch chỉ số đo của góc.
12. Các góc đặc biệt
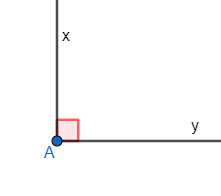
– Góc có số đo bằng 90o là góc vuông.
– Góc bẹt là góc có số đo bằng 180o.
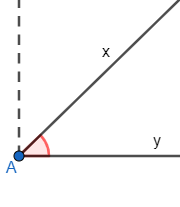
– Góc nhỏ hơn góc vuông là góc nhọn.
– Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù.
|
Góc vuông |
Góc nhọn |
Góc tù |
Góc bẹt |
|
|
|
|
|
|
∠xAy = 90o |
0o < ∠xAy < 90o |
90o < ∠xAy < 180o |
∠xAy = 180o |
II. Bài tập vận dụng
Bài 1: Cho hình vẽ:
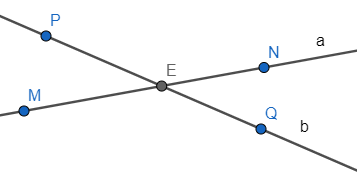
a) Điểm nào thuộc đường thẳng a (trả lời và viết kí hiệu)?
b) Điểm nào thuộc đường thẳng b (trả lời và viết kí hiệu)?
c) Điểm nào thuộc đường thẳng a nhưng không thuộc đường thẳng b (trả lời và viết kí hiệu)?
Lời giải:
a) Điểm thuộc đường thẳng a là điểm M; E; N
Kí hiệu: M ∈ a; N ∈ a; E ∈ a
b) Điểm thuộc đường thẳng b là điểm P; Q; E
Kí hiệu: P ∈ b; Q ∈ b; E ∈ b.
c) Điểm thuộc đường thẳng a nhưng không thuộc đường thẳng b là điểm M và điểm N
Kí hiệu: M ∈ a; N ∈ a và M ∉ b; N ∉ b.
Bài 2: Kể tên các đoạn thẳng có trong hình sau:
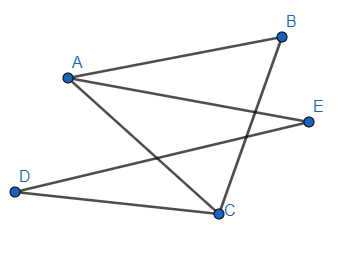
Lời giải:
Các đoạn thẳng có trong hình là: AB; AE; AC; BC; CD; DE.
Bài 3: Kể tên các góc có trong hình:
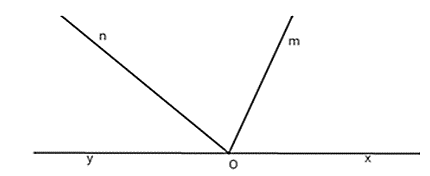
Lời giải:
Các góc có trong hình là: ∠xOm;∠xOn;∠xOy;∠mOn;∠mOy;∠nOy
Bài 4: Cho hai tia đối nhau Ox; Ox’. Trên tia Ox vẽ điểm A sao cho OA = 2cm. Trên tia Ox’ vẽ điểm B sao cho OB = 2cm. Hỏi O có là trung điểm của đoạn thẳng AB không? Vì sao?
Lời giải:

Vì A nằm trên tia Ox và B nằm trên tia Ox’ mà Ox và Ox’ đối nhau nên O nằm giữa A và B.
Mà OA = OB = 2cm nên O là trung điểm của đoạn thẳng AB.
Bài 5: Trên tia Ox vẽ hai điểm A và B sao cho OA = 3cm; OB = 8cm
a) Tính độ dài đoạn thẳng AB.
b) Gọi C là trung điểm của OB. Tính độ dài AC.
Lời giải:
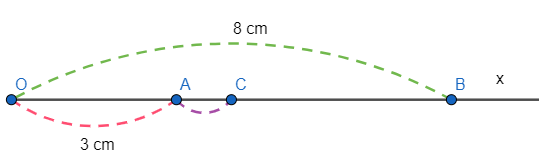
a) A, B thuộc tia Ox mà OA < OB nên A nằm giữa hai điểm O và B, ta có:
OA + AB = OB
Thay số:
3 + AB = 8
AB = 8 – 5
AB = 3cm
b) Vì C là trung điểm của OB nên OC = BC = 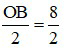 = 4cm.
= 4cm.
Hai điểm A và C cùng nằm trên tia Ox mà OA < OC nên A nằm giữa O và C
Ta có: OA + AC = OC
Thay số :
3 + AC = 4
AC = 4 – 3
AC = 1cm
Bài 6: Vẽ hai đường thẳng xx’ và yy’ cắt nhau tại điểm M sao cho góc xMy có số đo bằng 60o. Trên tia My’ lấy một điểm N khác M rồi vẽ đường thẳng aa’ đi qua N và song song với xx’.
a) Kể tên tất cả 8 góc có đỉnh M hoặc N, không kể các góc bẹt.
b) Dùng thước đo góc để đo 8 góc đã nêu trong câu a rồi sắp xếp chúng thành 2 nhóm, mỗi nhóm gồm các góc bằng nhau.
Lời giải:
* Cách vẽ:
– Vẽ đường thẳng xx’ bất kỳ.
– Lấy điểm M thuộc đường thẳng xx’.
– Vẽ đường thẳng yy’ đi qua M thỏa mãn ∠xMy = 60o.
– Trên tia My’ lấy điểm N (N khác M).
– Qua N kẻ đường thẳng aa’ song song với đường thẳng xx’.
* Ta có hình vẽ:
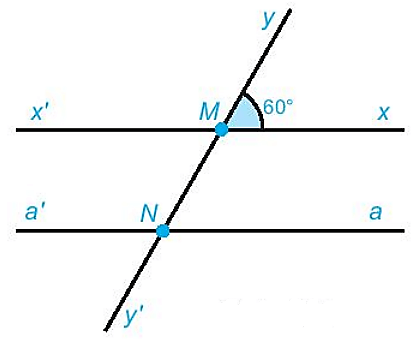
a) Các góc có đỉnh M (không kể góc bẹt) là:
∠xMy;∠x’My;∠xMy’;∠x’My’
Các góc có đỉnh N (không kể góc bẹt) là:
∠aNy;∠aNy’;∠a’Ny;∠a’Ny’
Vậy 8 góc có đỉnh M hoặc N (không kể các góc bẹt) là
∠xMy;∠x’My;∠xMy’;∠x’My’;∠aNy;∠aNy’;∠a’Ny;∠a’Ny’
b) Đo 8 góc đã nêu ở câu a, ta được:
∠xMy = ∠x’My’ = ∠aNy = ∠a’Ny’ = 60o
∠x’My = ∠xMy’ = ∠a’Ny = ∠aNy’ = 120o
Vậy 8 góc đã nêu ở câu a có thể xếp vào hai nhóm các góc bằng nhau như sau:
Nhóm 1: ∠xMy;∠x’My’;∠aNy;∠a’Ny
Nhóm 2: ∠x’My;∠xMy’;∠a’Ny;∠aNy’
Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:
Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên
Lý thuyết Chương 6: Phân số
Lý thuyết Chương 7: Số thập phân
Lý thuyết Chương 8: Những hình học cơ bản
Lý thuyết Chương 9: Dữ liệu và xác suất thực nghiệm