Lý thuyết Toán lớp 6 Chương 5: Phân số
Video giải Toán 6 Chương 5: Phân số – Chân trời sáng tạo
A. Lý thuyết Toán lớp 6 Chương 5: Phân số
1. Khái niệm phân số
Ta gọi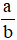 
, trong đó 
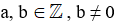là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số 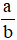đọc là a phần b.
2. Phân số bằng nhau
Hai phân số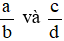 
được gọi là bằng nhau, viết là 
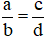, nếu a . d = b . c.
Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số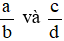
3. Biểu diễn số nguyên ở dạng phân số
Mỗi số nguyên n có thể coi là phân số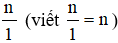 
. Khi đó số nguyên n được biểu diễn ở dạng phân số 
.
4. Tính chất cơ bản của phân số
– Tính chất 1: Nếu nhân cả tử số và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.
– Áp dụng tính chất 1, ta có thể quy đồng mẫu số hai phân số bằng cách nhân tử và mẫu mỗi phân số với số nguyên thích hợp.
2. Tính chất 2
– Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.
Áp dụng tính chất 2, ta có thể rút gọn phân số bằng cách chia cả tử và mẫu cho cùng ước chung khác 1 và −1.
5. So sánh hai phân số có cùng mẫu
Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
6. So sánh hai phân số khác mẫu
Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.
7. Áp dụng quy tắc so sánh phân số
Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.
Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là:
Nếu có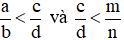 
thì ta có 
.
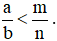Nhận xét:
– Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.
– Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.
8. Phép cộng hai phân số
Quy tắc cộng hai hai phân số cùng mẫu: Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.
Quy tắc cộng hai phân số khác mẫu: Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng
Một số tính chất của phép cộng phân số: Phép cộng phân số có các tính chất giao hoán và kết hợp, cộng một phân số với 0 ta được chính nó.
9. Số đối
Hai phân số là đối nhau nếu tổng của chúng bằng 0.
Kí hiệu số đối của phân số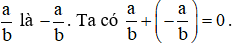 
.
Mà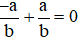 
nên ta có: 
.
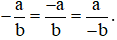10. Phép trừ hai phân số
Muốn trừ một phân số cho một phân số, ta lấy phân số thứ nhất cộng với số đối của phân số thứ hai.
Quy tắc dấu ngoặc:
– Khi bỏ ngoặc có dấu cộng (+) đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.
– Khi bỏ ngoặc có dấu trừ (−) đằng trước, ta phải đổi dấu tất cả các số hạng trong ngoặc.
Chú ý: Ta thực hiện được phép cộng và phép trừ phân số với số nguyên bằng cách viết số nguyên ở dạng phân số.
11. Nhân hai phân số
Quy tắc: Muốn nhân hai phân số, ta nhân tử số với nhau và nhân hai mẫu số với nhau.
– Một số tính chất của phép nhân phân số: Phép nhân phân số có các tính chất: giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng.
Chú ý: Khi nhân một phân số với 1 ta được chính nó.
12. Chia phân số
Quy tắc chia phân số: Muốn chia một phân số cho một phân số khác 0 ta nhân phân số thứ nhất với phân số có tử số là mẫu số của phân số thứ hai và mẫu số là tử số của phân số thứ nhất.
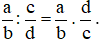
Chú ý: Ta thực hiện được phép nhân và phép chia phân số với số nguyên bằng cách viết số nguyên dưới dạng phân số.
13. Tính giá trị phân số của một số
Quy tắc 1: Muốn tính giá trị phân số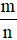 
của số a, ta tính 
.
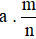14. Tìm một số khi biết giá trị phân số của số đó
Quy tắc 2: Muốn tìm một số khi biết giá trị phân số 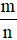của nó là b, ta tính 
.
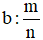15. Hỗn số
Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết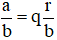 
và gọi 
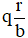là hỗn số.
Chú ý: Với hỗn số 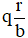người ta gọi q là phần số nguyên và 
là phần phân số của hỗn số.
16. Đổi hỗn số ra phân số
Ta biết viết phân số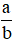 
với a > b > 0 thành hỗn số .
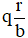Ngược lại, ta đổi được hỗn số 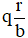thành phân số, theo quy tắc sau:
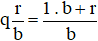
B. Bài tập tự luyện
Bài 1. Đọc các phân số sau:
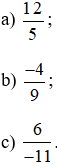
Lời giải:
a) Phân số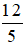 
có tử số là 12, mẫu số là 5.
Đọc là: Mười hai phần năm;
b) Phân số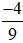 
có tử số là −4, mẫu số là 9.
Đọc là: Âm bốn phần chín;
c) Phân số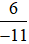 
có tử số là 6, mẫu số là −11.
Đọc là: Sáu phần âm mười một.
Bài 2. Vẽ lại hình bên và tô màu để phân số biểu thị phần tô màu bằng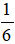 
.
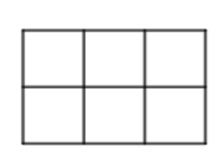
Lời giải:
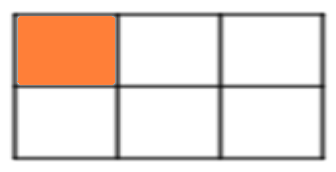
Phân số 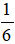có tử số là 1, mẫu số là 6.
Phân số biểu thị phần tô màu bằng 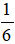tức là hình đó được chia thành 6 phần bằng nhau và tô màu 1 phần.
Ta có hình vẽ biểu thị phần tô màu bằng 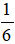như sau:
Bài 3. Tìm cặp phân số bằng nhau trong các cặp phân số sau:
Lời giải:
a)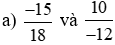 
So sánh hai tích: (−15) . (−12) và 18 . 10;
Ta có: (−15) . (−12) = 15 . 12 = 180 và 18 . 10 = 180.
Nên (−15) . (−12) = 18 . 10.
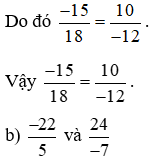
So sánh hai tích: (−22) . (−7) và 5 . 24;
Ta có: (−22) . (−7) = 22 . 7 = 154 và 5 . 24 = 120.
Nên (−22) . (−7) ≠ 5 . 24.
Do đó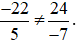 
.
Vậy hai phân số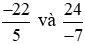 
không bằng nhau.
Bài 4. Một bể bơi có máy bơm A để bơm nước vào bể. Nếu bể không có nước máy bơm sẽ bơm đầy bể trong 11 giờ. Cũng bể bơi đó, có máy bơm B dùng để tháo nước ra khỏi bể khi vệ sinh bể bơi. Nếu bể đầy nước, máy bơm B sẽ bơm hết nước trong bể chỉ trong 7 giờ.
Điền phân số với tử và mẫu là số nguyên thích hợp vào bảng sau đây:
Lời giải:
– Máy bơm A sẽ bơm từ khi chưa có nước đến khi đầy bể mất 11 giờ nên phân số ở mỗi ô có mẫu số là 11, tử số là số giờ bơm tương ứng.
– Máy bơm B sẽ tháo nước từ khi đầy bể đến khi hết sạch nước trong bể là 7 giờ nên phân số ở mỗi ô có mẫu số là 7, tử số là số âm của giờ bơm tương ứng.
Ta có bảng sau:
Bài 5. Áp dụng tính chất 1 và tính chất 2 để tìm một phân số bằng mỗi phân số sau:
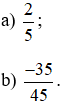
Lời giải:
a) Ta có thể nhân cả tử và mẫu của phân số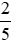 
với một số nguyên khác 0 bất kỳ để được phân số mới bằng phân số đã cho (theo tính chất 1).
Chẳng hạn: Nhân cả tử và mẫu của phân số 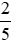với 4, ta được:
(theo tính chất 1).
Vậy một phân số bằng phân số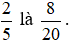 
.
b) Ta có thể chia cả tử và mẫu của một phân số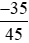 
cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho (theo tính chất 2).
Chẳng hạn: Chia cả tử và mẫu của phân số 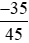cho 5, ta được:
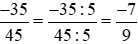(theo tính chất 2).
Vậy một phân số bằng phân số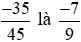 
.
Bài 6. Rút gọn các phân số sau:
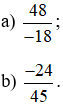
Lời giải:
a) Chia cả tử và mẫu của phân số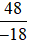 
cho 6, ta được:
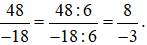
b) Chia cả tử và mẫu của phân số 
cho 3, ta được:
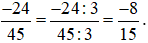
Bài 7. Đưa mỗi phân số sau về phân số có mẫu số dương rồi quy đồng các phân số sau:
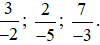
Lời giải:
Đưa các phân số trên về phân số có mẫu số dương như sau:
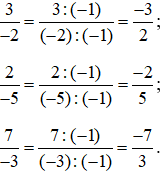
Quy đồng các phân số trên ta được:
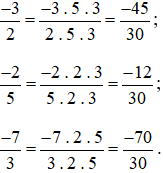
Bài 8. Dùng phân số có mẫu số dương nhỏ nhất để biểu thị xem số phút sau đây chiếm bao nhiêu phần của một giờ?
a) 36 phút;
b) 25 phút;
Lời giải:
Đổi: 1 giờ = 60 phút.
Để tìm phân số biểu thị số phút chiếm bao nhiêu phần của một giờ, ta lấy số phút chia cho 60.
a) Phân số biểu thị 36 phút chiếm số phần của một giờ là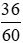 
.
Rút gọn phân số, ta được: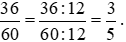 
.
Vậy phân số có mẫu số dương nhỏ nhất để biểu thị 36 phút là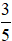 
giờ.
b) Phân số biểu thị 25 phút chiếm số phần của một giờ là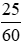 
.
Rút gọn phân số, ta được: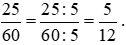 
.
Vậy phân số có mẫu số dương nhỏ nhất để biểu thị 25 phút là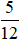 
giờ.
Bài 9. So sánh hai phân số.
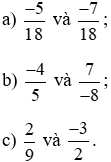
Lời giải:
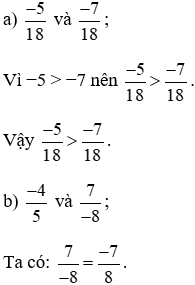
Quy đồng hai phân số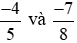 
ta thực hiện:
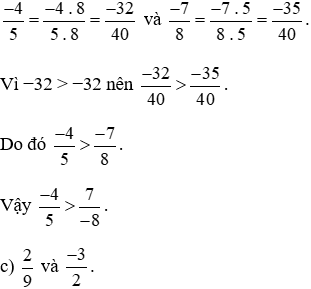
Ta có 
(vì phân số này là phân số dương).
Và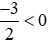 
(vì phân số này là phân số âm).
Theo tính chất bắc cầu, phân số dương lớn hơn phân số âm nên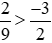 
.
Vậy .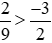
Bài 10. So sánh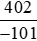 
và −4.
Lời giải:
Cách 1: Đưa số nguyên và phân số về dạng phân số có cùng mẫu số dương, rồi so sánh tử số của hai phân số.
Ta có:
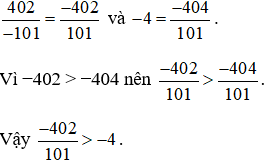
Cách 2: Đưa số nguyên về dạng phân số có mẫu số là 1, tử số là số nguyên đó, sau đó quy đồng mẫu số hai phân số đó (đưa hai phân số về cùng mẫu số dương).
Ta có: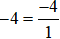 
.
Quy đồng mẫu số hai phân số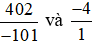 
, ta được:
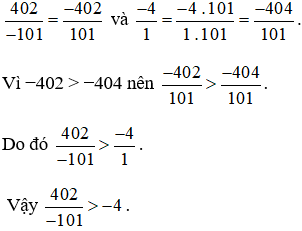
Bài 11. Sắp xếp các số theo thứ tự tăng dần: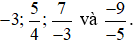 
.
Lời giải:
Để sắp xếp các phân số theo thứ tự tăng dần, ta làm như sau:
Bước 1: Đưa các phân số vào hai nhóm: nhóm các phân số dương và nhóm các phân số âm.
– Phân số dương là phân số có tử số và mẫu số là các số nguyên cùng dấu.
– Phân số âm là phân số có tử số và mẫu số là các số nguyên trái dấu.
Bước 2: So sánh các phân số dương với nhau, các phân số âm với nhau (bằng cách đưa về cùng mẫu số dương rồi so sánh tử số).
Bước 3: Sắp xếp các phân số trên theo thứ tự từ tăng dần (phân số âm luôn bé hơn phân số dương).
Ta có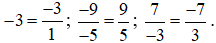 
.
+ Các phân số dương: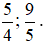 
.
+ Các phân số âm: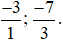 
.
Ta so sánh các phân số dương với nhau, các phân số âm với nhau:
+ So sánh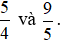 
.
Mẫu số chung: 20.
Ta thực hiện: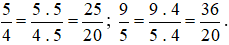 
.
Vì 25 < 36 nên 
.
+ So sánh 
Mẫu số chung: 3.
Ta thực hiện: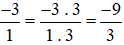 
và giữ nguyên phân số 
.
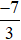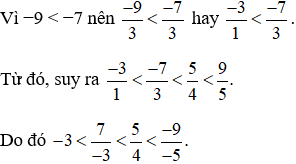
Vậy ta sắp xếp được theo thứ tự tăng dần như sau: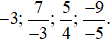 
Bài 12. Bình đọc hết một quyển sách trong 3 ngày. Ngày thứ nhất đọc được 
quyển sách, ngày thứ hai đọc được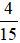 
quyển sách, ngày thứ ba đọc được 
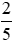quyển sách. Hỏi trong ba ngày đó thì ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất?
Lời giải:
Bài toán đưa về sắp xếp các phân số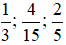 
theo thứ tự tăng dần hoặc giảm dần. Sau đó kiểm tra xem ngày nào Bình đọc được nhiều nhất, ngày nào đọc được ít nhất.
Quy đồng mẫu số các phân số 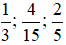, ta được:
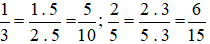giữ nguyên phân số .
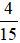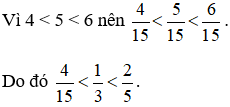
Vậy ngày thứ hai Bình đọc được nhiều nhất tương ứng với 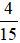quyển sách, ngày thứ ba Bình đọc được ít nhất tương ứng với 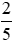quyển sách.
Bài 13. Tính giá trị biểu thức sau theo hai cách (có một cách dùng tính chất phép cộng phân số):
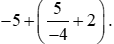
Lời giải:
Cách 1: Thực hiện đúng theo thứ tự phép tính (thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau).
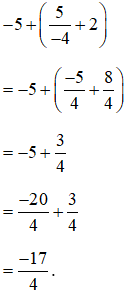
Cách 14: Dùng tính chất bỏ ngoặc. Sau đó sử dụng tính chất giao hoán và kết hợp của phép cộng.
Bài 2. Tìm số đối của:
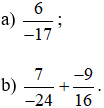
Lời giải:
a) Thêm dấu trừ trước phân số và rút gọn.
Số đối của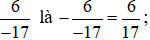 
b) Tính giá trị biểu thức rồi tìm số đối của kết quả tìm được hoặc đặt dấu trừ trước ngoặc chưa biểu thức.
Ta có: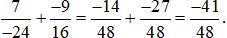 
.
Số đối của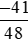 
là phân số 
.
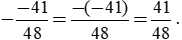Vậy số đối của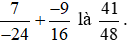 
.
Bài 15. Người ta mở hai vòi nước cùng chảy vào một bể. Vòi thứ nhất mỗi giờ chảy được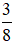 
bể, vòi thứ hai mỗi giờ chảy được 
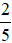bể. Nếu mở đồng thời cả hai vòi, mỗi giờ được mấy phần bể?
Lời giải:
Lượng nước hai vòi chảy được sau mỗi giờ bằng tổng lượng nước mỗi vòi chảy được mỗi giờ.
Nếu mở đồng thời cả hai vòi, mỗi giờ được:
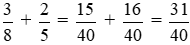(phần bể).
Vậy nếu mở đồng thời cả hai vòi, mỗi giờ được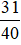 
phần bể.
Bài 16. Tìm x biết:
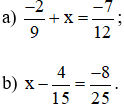
Lời giải:
Chuyển x sang một vế, bài toán đưa về tính tổng (hiệu) hai phân số.
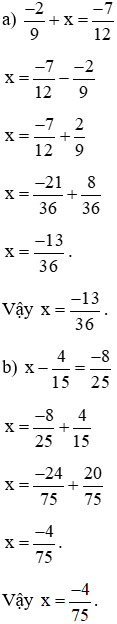
Bài 17. Tính giá trị biểu thức (tính hợp lí nếu có thể).
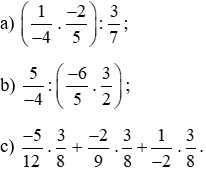
Lời giải:
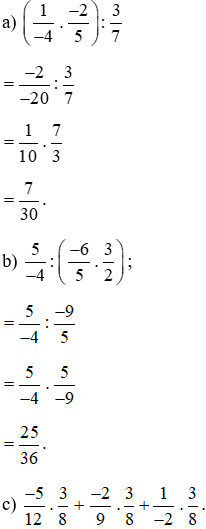
Bài 18. Tìm x, biết:
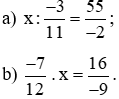
Lời giải:
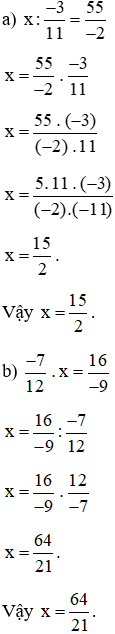
Bài 19. Một hình chữ nhật có chiều rộng là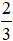 
m, diện tích là 
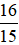m2. Tính chiều dài của hình chữ nhật.
Lời giải:
Chiều dài của hình chữ nhật là:
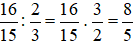(m)
Vậy chiều dài của hình chữ nhật là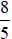 
m.
Bài 20. Tính:
a)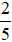 
của 25 m là bao nhiêu mét?
b)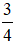 
của 20 giờ là bao nhiêu giờ?
Lời giải:
a) Giá trị 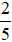của 25 m là:
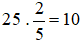(m).
Vậy giá trị 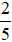của 25 m là 10 m.
b) Giá trị 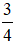của 20 giờ là:
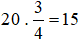(giờ).
Vậy giá trị 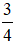của 20 giờ là 15 giờ.
Bài 21. Tìm một số, biết:
a)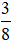 
của số đó là 162;
b) −114 là 
.
Lời giải:
a) 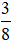của số đó là 162 thì số cần tìm là:
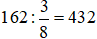
Vậy số cần tìm là 432.
b) −114 là của số đó thì số cần tìm là:
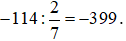
Vậy số cần tìm là −399.
Bài 22. Một bác nông dân thu hoạch và mang cam ra chợ bán. Bác đã thu hoạch được 30 kg, ứng với 
số cam. Hỏi bác nông dân đã mang bao nhiêu kilôgam cam ra chợ bán?
Lời giải:
Số cam bác nông dân mang ra chợ bán là:
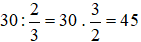(kg)
Vậy bác nông dân đã mang 45 kg cam ra chợ bán.
Bài 23. Viết các hỗn số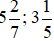 
dưới dạng phân số.
Lời giải:
Các hỗn số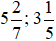 
chuyển sang phân số như sau:
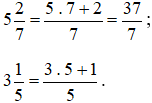
Bài 24. Tính giá trị biểu thức: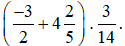 
.
Lời giải:
Bài 25. Sắp xếp các độ dài sau theo thứ tự từ nhỏ đến lớn:
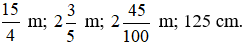
Lời giải:
Đổi: 1 m = 100 cm.
Khi đổi từ m sang cm, ta chia số đó cho 100 (viết dưới dạng phân số).
Khi đó,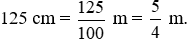 
.
Ta có: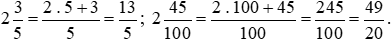 
.
Quy đồng các phân số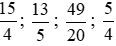 
, ta thực hiện:
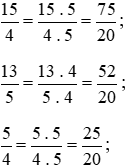
Giữ nguyên phân số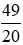 
.
Vì 25 < 49 < 52 < 75 nên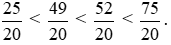 
.
Do đó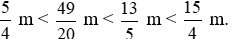 
.
Vậy các độ dài theo thứ tự từ nhỏ đến lớn là:
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Chương 4: Một số yếu tố thống kê
Lý thuyết Chương 5: Phân số
Lý thuyết Chương 6: Số thập phân
Lý thuyết Chương 7: Hình học trực quan
Lý thuyết Chương 8: Hình học phẳng và các hình học cơ bản