Bộ 20 Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – 2024 – Cánh diều

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 6 Cánh diều bản word có lời giải chi tiết:

B1:   –

B2:   – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

 

Bộ 20 Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Cánh diều – Đề 1

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

A. Đề bài

I. Phần trắc nghiệm (4 điểm)

Câu 1: Tập hợp nào dưới đây có 5 phần tử?

A. A = {x \( \in {\mathbb{N}^*}\)| x > 3}

B. B = {x \( \in \mathbb{N}\)| x < 6}

C. C = {x \( \in \mathbb{N}\)| x ≤ 4}

D. D = {x \( \in {\mathbb{N}^*}\)| 4 < x ≤ 8}

Câu 2: Cho tập hợp M các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3. Phần tử nào dưới đây không thuộc tập hợp M?

A. 13                    B. 23

C. 33                    D. 43

Câu 3: Số 1 080 chia hết cho bao nhiêu số trong các số sau đây: 2, 3, 4, 5, 6, 8, 9, 12, 24, 25?

A. 10 số                B. 9 số

C. 8 số                  D. 7 số

Câu 4: Hằng gấp được 97 ngôi sao và xếp vào các hộp, mỗi hộp 8 ngôi sao. Số ngôi sao còn thừa không xếp vào hộp là:

A. 5 ngôi sao

B. 1 ngôi sao

C. 6 ngôi sao

D. 2 ngôi sao

Câu 5: Phân tích số 154 ra thừa số nguyên tố được:

A. 154 = 2 . 7 . 11

B. 154 = 1 . 5 . 4

C. 154 = 2² . 3 . 5

D. 154 = 2 . 7 . 13

Câu 6: Hình nào dưới đây là hình vẽ chỉ tam giác đều?

A.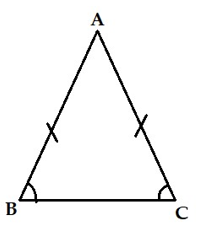 

B.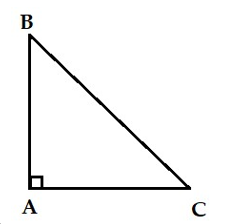  

C.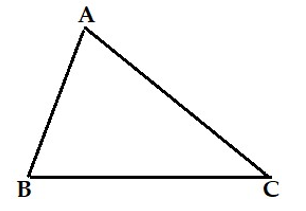 

D.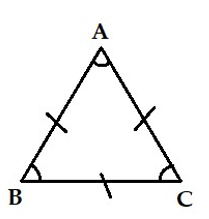 

Câu 7: Hai đường chéo hình thoi có độ dài lần lượt bằng 16 cm và 12 cm. Diện tích của hình thoi là:

A. 90 cm²              B. 96 cm²  

C. 108 cm²            D. 120 cm²

Câu 8: Chọn câu sai trong các câu dưới đây?

Cho hình vẽ

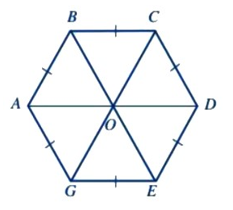
Lục giác đều ABCDEG là hình có:

A. Các góc ở các đỉnh A, B, C, D, E, G, O bằng nhau.

B. Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.

C. Ba đường chéo chính cắt nhau tại điểm O.

D. Ba đường chéo chính bằng nhau: AD = BE = CG.

II. Phần tự luận (6 điểm)

Bài 1 (2 điểm):

1) Thực hiện các phép tính:

a) 30 . 75 + 25 . 30 – 150;

b) 160 – (4 . 5² – 3 . 2³);

c) [36 . 4 – 4 . (82 – 7 . 11)²] : 4 – 2022⁰.

2) Tìm BCNN của các số 28, 54.

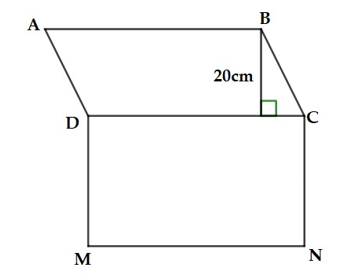
Bài 2 (1,5 điểm): Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.

Bài 3 (2 điểm): Một đội y tế gồm 48 bác sĩ và 108 y tá. Hỏi có thể chia đội y tế thành nhiều nhất bao nhiêu tổ để số bác sĩ và y tá được chia đều vào các tổ?

Bài 4 (0,5 điểm): Chứng tỏ A chia hết cho 6 với A = 2 + 2² + 2³ + 2⁴ + … + 2¹⁰⁰.

—

B. Đáp án và hướng dẫn giải

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: C	Câu 2: A	Câu 3: B	Câu 4: B
Câu 5: A	Câu 6: D	Câu 7: B	Câu 8: A

 

Hướng dẫn chi tiết

Câu 1:

Viết các tập hợp đã cho dưới dạng liệt kê các phần tử ta được

A = {4; 5; 6; … }   (tập hợp A các số tự nhiên lớn hơn 3)

B = {0; 1; 2; 3; 4; 5} (tập hợp B các số tự nhiên nhỏ hơn 6)

C = {0; 1; 2; 3; 4}  (tập hợp C các số tự nhiên nhỏ hơn hoặc bằng 4)

D = {5; 6; 7; 8}  (tập hợp D các số tự nhiên lớn hơn 4 và nhỏ hơn hoặc bằng 8)

Vậy ta thấy tập hợp C có 5 phần tử.

Chọn đáp án C.

Câu 2:

Tập hợp M gồm các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3.

Ta thấy các số 13, 23, 33, 43 đều có chứa chữ số 3, nhưng 13 < 14 nên 13 không thuộc tập hợp M.

Chọn đáp án A.

Câu 3:

Số 1 080 có chữ số tận cùng là 0 nên nó chia hết cho cả 2 và 5.

Số 1 080 có tổng các chữ số là 1 + 0 + 8 + 0 = 9 chia hết cho 3 và 9 nên nó chia hết cho cả 3 và 9.

Ngoài ra: 1 080 : 4 = 270; 1 080 : 6 = 180; 1 080 : 8 = 135; 1 080 : 12 = 90; 1 080 : 24 = 45; 1 080 : 25 = 43 (dư 5).

Vậy số 1 080 chia hết cho các số: 2, 3, 4, 5, 6, 8, 9, 12, 24.

Do đó nó chia hết cho 9 số trong các số đã cho.

Chọn đáp án B.

Câu 4:

Mỗi hộp có 8 ngôi sao nên ta thực hiện phép chia:

97 : 8 = 12 (dư 1)

Vậy còn thừa 1 ngôi sao không xếp vào hộp.

Chọn đáp án B.

Câu 5:

Ta phân tích 154 ra thừa số nguyên tố:

 

Vậy 154 = 2 . 7 . 11.

Chọn đáp án A.

Câu 6:

Tam giác đều là hình tam giác có 3 cạnh bằng nhau và 3 góc bằng nhau, vậy trong các hình đã cho, hình vẽ D chỉ tam giác đều.

Chọn đáp án D.

Câu 7:

Diện tích hình thoi bằng \(\frac{1}{2}\) tích độ dài hai đường chéo.

Vậy diện tích của hình thoi có độ dài hai đường chéo lần lượt là 16 cm và 12 cm là:

\(S = \frac{1}{2}.16.12 = 96\) (cm²).

Chọn đáp án B.

Câu 8:

Lục giác đều ABCDEG có các tính chất:

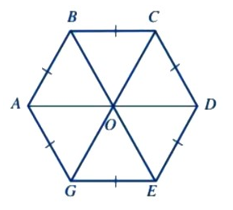
+ Các góc ở các đỉnh A, B, C, D, E, G bằng nhau.

+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.

+ Ba đường chéo chính AD, BE, CG cắt nhau tại điểm O.

+ Ba đường chéo chính bằng nhau: AD = BE = CG.

Vậy đáp án A sai (vì góc ở đỉnh O không bằng các góc ở đỉnh của lục giác).

Chọn đáp án A.

II. Phần tự luận

Bài 1:

1)

a) 30 . 75 + 25 . 30 – 150

= 30 . (75 + 25) – 150

= 30 . 100 – 150

= 3 000 – 150 = 2 850

b) 160 – (4 . 5² – 3 . 2³)

= 160 – (4 . 25 – 3 . 8)

= 160 – (100 – 24)

= 160 – 76 = 84

c) [36 . 4 – 4 . (82 – 7 . 11)²] : 4 – 2022⁰ 

= [36 . 4 – 4 . (82 – 77)²] : 4 – 1

= [36 . 4 – 4 . 5²] : 4 – 1

= [36 . 4 – 4 . 25] : 4 – 1

= [4 . (36 – 25)] : 4 – 1

= 4 . 11 : 4 – 1 = 11 – 1 = 10

2)

Đề tìm BCNN của 28 và 54, ta phân tích các số đó ra thừa số nguyên tố.

Ta có: 28 = 4 . 7 = 2² . 7

54 = 6 . 9 = 2 . 3 . 3² = 2 . 3³

Vậy BCNN(28, 54) = 2² . 3³ . 7 = 4 . 27 . 7 = 756.

Bài 2:

Nửa chu vi hình chữ nhật DCNM là: 180 : 2 = 90 (cm)

Khi đó: MN + CN  = 90 (cm)

Chiều dài MN gấp 4 lần chiều rộng CN

Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)

Chiều dài MN (hay CD) của hình chữ nhật DCNM là: 90 : 5 . 4 = 72 (cm)

Chiều rộng CN (hay DM) của hình chữ nhật DCNM là: 90 – 72 = 18 (cm)

Diện tích hình chữ nhật DCMN là: 18 . 72 = 1 296 (cm²)

Diện tích hình bình hành ABCD là: 72 . 20 = 1 440 (cm²)

Diện tích hình H là: 1 296 + 1 440 = 2 736 (cm²).

Bài 3:

Gọi x là số tổ nhiều nhất được chia (x là số tự nhiên khác 0).

Vì số bác sĩ được chia đều vào mỗi tổ nên 48 ⁝ x

Số y tá được chia đều vào mỗi tổ nên 108 ⁝ x

Do đó x là ước chung của 48 và 108, mà x là nhiều nhất nên x là ƯCLN của 48 và 108.

Ta có: 48 = 2⁴ . 3

108 = 2² . 3³

Suy ra ƯCLN(48, 108) = 2² . 3 = 12 hay x = 12 (thỏa mãn).

Vậy có thể chia được nhiều nhất 12 tổ.

Bài 4:

A = 2 + 2² + 2³ + 2⁴ + … + 2¹⁰⁰

A = (2 + 2²) + (2³ + 2⁴) + … + (2⁹⁹ + 2¹⁰⁰)

A = 6 + 2² . (2 + 2²) + … + 2⁹⁸ . (2 + 2²)

A = 6 + 2² . 6 + … + 2⁹⁸ . 6

A = 6 . (1 + 2² + … + 2⁹⁸)

Vậy A chia hết cho 6 (theo tính chất chia hết của một tích).

Bộ 20 Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Cánh diều – Đề 2

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

A. Đề bài

I. Phần trắc nghiệm (4 điểm)

Câu 1: Tập hợp A các số tự nhiên nhỏ hơn 7 được viết là:

A. A = {x \( \in {\mathbb{N}^*}\)| x < 7}

B. A = {x \( \in \mathbb{N}\)| x < 7}

C. A = {x \( \in {\mathbb{N}^*}\)| x ≤ 7}

D. A = {x \( \in \mathbb{N}\)| x > 7}

Câu 2: Cho tập hợp B = {1; 8; 12; 21}. Phần tử nào dưới đây không thuộc tập hợp B?

A. 1                      B. 12

C. 21                    D. 18

Câu 3: Trong các số tự nhiên dưới đây, số nào là số nguyên tố?

A. 101                   B. 114

C. 305                   D. 303

Câu 4: Số nào dưới đây chia hết cho 5 nhưng không chia hết cho 3?

A. 120                   B. 195

C. 215                   D. 300

Câu 5: Diện tích của hình vuông có độ dài cạnh a = 4 . 5 + 2² . (8 – 3) (cm) là:

A. 160 cm²            B. 400 cm² 

C. 40 cm²              D. 1 600 cm²

Câu 6: Hình bình hành không có tính chất nào dưới đây?

A. Hai cạnh đối bằng nhau

B. Hai cạnh đối song song với nhau

C. Hai góc đối bằng nhau

D. Bốn cạnh bằng nhau

Câu 7: Cho 24 ⁝ (x + 6) và 3 ≤ x < 8, với x là số tự nhiên. Vậy x có giá trị bằng:

A. 5                      B. 6

C. 7                      D. 8

Câu 8: Cho hình thoi có độ dài hai đường chéo bằng 8 cm và 10 cm. Diện tích của hình thoi là:

A. 40 cm²              B. 60 cm²

C. 80 cm²              D. 100 cm²

II. Phần tự luận (6 điểm)

Bài 1 (2 điểm): Thực hiện phép tính:

a) 162 + 475 + 173 + 227 + 525 + 438;

b) 25 . 6 + 5 . 5 . 29 – 45 . 5;

c) 2 . [(7 – 3³ : 3²) : 2² + 99] – 100;

d) (5²⁰²² + 5²⁰²¹) : 5²⁰²¹.

Bài 2 (1 điểm): Một mảnh vườn hình chữ nhật có chiều dài bằng 40 m và chu vi bằng 140 m. Tính diện tích của mảnh vườn hình chữ nhật đó.

Bài 3 (2 điểm): Lớp 6A có 42 học sinh, lớp 6B có 54 học sinh và lớp 6C có 48 học sinh. Cô phụ trách đã xếp đều số học sinh của 3 lớp thành một số hàng như nhau. Tính số hàng nhiều nhất có thể xếp được.

Bài 4 (1 điểm): Chứng tỏ rằng: (10²⁸ + 8) ⁝ 9.

—

B. Đáp án và hướng dẫn giải

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: B	Câu 2: D	Câu 3: A	Câu 4: C
Câu 5: D	Câu 6: D	Câu 7: B	Câu 8: A

 

Hướng dẫn chi tiết

Câu 1:

Gọi x là số tự nhiên thuộc tập hợp A.

Ta có x là số tự nhiên nên x \( \in \mathbb{N}\)

Mà các số tự nhiên thuộc tập hợp A nhỏ hơn 7 nên x < 7.

Vậy ta viết tập hợp A như sau: A = {x \( \in \mathbb{N}\)| x < 7}.

Chọn đáp án B.

Câu 2:

Ta có: B = {1; 8; 12; 21}

Nhận thấy số 18 không phải là phần tử của tập hợp B nên 18 không thuộc tập hợp B.

Chọn đáp án D.

Câu 3:

Lý thuyết: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước. Một số là hợp số thì không thể là số nguyên tố.

Trong các số đã cho, ta thấy:

+) 114 có chữ số tận cùng là 4 nên nó chia hết cho 2, do đó 114 là hợp số vì ngoài hai ước là 1 và 114 thì nó còn có thêm ít nhất một ước nữa là 2.

+) 305 có chữ số tận cùng là 5 nên nó chia hết cho 5, do đó 305 là hợp số vì ngoài hai ước là 1 và 305 thì nó còn có thêm ít nhất một ước nữa là 5.

+) 303 có tổng các chữ số là 3 + 0 + 3 = 6 chia hết cho 3 nên nó chia hết cho 3, do đó 303 là hợp số vì ngoài hai ước là 1 và 303 thì nó còn có thêm ít nhất một ước nữa là 3.

+) Số 101 lớn hơn 1, chỉ có hai ước là 1 và 101 nên nó là số nguyên tố.

Chọn đáp án A.

Câu 4:

Các số 120, 195, 215, 300 đều chia hết cho 5 (vì có tận cùng là 0 hoặc 5).

Số 215 có tổng các chữ số là 2 + 1 + 5 = 8 không chia hết cho 3 nên 215 không chia hết cho 3.

Vậy số 215 chia hết cho 5 nhưng không chia hết cho 3.

Chọn đáp án C.

Câu 5:

Ta có: a = 4 . 5 + 2² . (8 – 3) = 20 + 4 . 5 = 20 + 20 = 40 (cm)

Diện tích hình vuông có cạnh a là:

S = a . a = 40 . 40 = 1 600 (cm²).

Chọn đáp án D.

Câu 6:

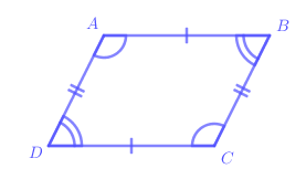
Hình bình hành ABCD có các tính chất:

+ Hai cạnh đối AB và CD, AD và BC song song với nhau.

+ Hai cạnh đối AB và CD, AD và BC bằng nhau.

+ Hai góc ở đỉnh A và C bằng nhau, hai góc ở đỉnh B và D bằng nhau (hai góc đối bằng nhau)

Do đó hình bình hành không có tính chất: Bốn cạnh bằng nhau.

Chọn đáp án D.

Câu 7:

Ta có: x là số tự nhiên thỏa mãn 3 ≤ x < 8

Khi đó: x \( \in \){3; 4; 5; 6; 7}

Lại có: 24 ⁝ (x + 6) (*)

Ta thử thay lần lượt các giá trị của x vào (*), ta thấy x = 6 thỏa mãn vì x + 6 = 6 + 6 = 12, 24 chia hết cho 12.

Vậy x có giá trị là 6.

Chọn đáp án B.

Câu 8:

Diện tích hình thoi bằng \(\frac{1}{2}\)lần tích độ dài hai đường chéo.

Do đó diện tích hình thoi có độ dài hai đường chép bằng 8 cm và 10 cm là:

S = \(\frac{1}{2}.8.10\) = 40 (cm²)

Chọn đáp án A.

II. Phần tự luận

Bài 1:

a) 162 + 475 + 173 + 227 + 525 + 438

= (162 + 438) + (475 + 525) + (173 + 227)

= 600 + 1 000 + 400

= (600 + 400) + 1 000

= 1 000 + 1 000

= 2 000

b) 25 . 6 + 5 . 5 . 29 – 45 . 5

= 25 . 6 + 25 . 29 – 9 . 5 . 5  

= 25 . 6 + 25 . 29 – 25 . 9

= 25 . (6 + 29 – 9)

= 25 . 26 = 650

c) 2 . [(7 – 3³ : 3²) : 2² + 99] – 100

= 2 . [(7 – 3) : 4 + 99] – 100

= 2 . [4 : 4 + 99] – 100

= 2 . (1 + 99) – 100

= 2 . 100 – 100 = 100

d) (5^{2 022} + 5^{2 021}) : 5^{2 021}

= 5^{2 022} : 5^{2 021} + 5^{2 021} : 5^{2 021} 

= 5^{2 022 – 2 021}  + 5^{2 021 – 2 021}  

= 5¹ + 5⁰

= 5 + 1 = 6

Bài 2:

Nửa chu vi của hình chữ nhật là: 140 : 2 = 70 (m)

Chiều rộng mảnh vườn hình chữ nhật là: 70 – 40 = 30 (m)

Diện tích mảnh vườn hình chữ nhật là: 40 . 30 = 1 200 (m²).

Bài 3:

Gọi số hàng có thể xếp là x (x \( \in {\mathbb{N}^*}\); hàng)

Theo đề bài có: 42 ⁝ x; 54 ⁝ x; 48 ⁝ x và x lớn nhất nên x là ƯCLN của 42, 54 và 48.

Ta tìm ƯCLN này bằng cách phân tích các số 42, 54, 48 ra thừa số nguyên tố.

Ta có: 42 = 2 . 3 . 7

54 = 2 . 3³

48 = 2⁴ . 3

Suy ra ƯCLN(42, 54, 48) =  2 . 3 = 6 hay x = 6 (thỏa mãn).

Vậy có thể xếp được nhiều nhất là 6 hàng để thỏa mãn yêu cầu bài toán.

Bài 4:

Có 10²⁸ có dạng 10….000 (28 chữ số 0) nên 10²⁸ + 8 có dạng 10….008 (27 chữ số 0) nên số 10²⁸ + 8 sẽ chia hết cho 9 (tổng các chữ số bằng 9).

 

Bộ 20 Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Cánh diều – Đề 3

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

A. Đề bài

I. Phần trắc nghiệm (4 điểm)

Câu 1: Tập hợp A các số tự nhiên x thỏa mãn 4 < x ≤ 9 là:

A. A = {4; 5; 6; 7; 8; 9}

B. A = {x \( \in \mathbb{N}\)| 4 < x ≤ 9}

C. A = {5; 6; 7; 8}

D. A = {x \( \in \mathbb{N}\)| 4 ≤ x ≤ 9}

Câu 2: Có bao nhiêu số nguyên tố nhỏ hơn 25?

A. 9 số                  B. 10 số

C. 11 số                D. 12 số

Câu 3: Quan sát hình vẽ dưới đây và chọn câu trả lời đúng:

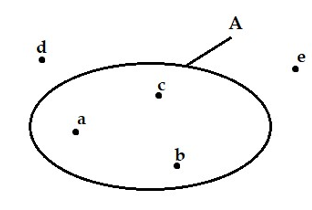
A. \(a \in A\)                   B. \(d \in A\)

C. \(b \notin A\)             D. \(c \notin A\)

Câu 4: Viết tập hợp A các ước của số 16 là:

A. A = {1; 2; 3; 5}

B. A = {1; 2; 4; 8; 16}

C. A = {1; 2; 3; 4; 16}

D. A = {1; 2; 3; 4; 5; 6; 10; 16}

Câu 5: Đặc điểm nào dưới đây không phải là tính chất của hình vuông ABCD?

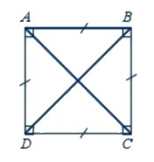
A. AB = BC = CD = DA

B. AB và CD song song với nhau

C. AD và CD song song với nhau

D. Hai đường chéo bằng nhau

Câu 6: Bác Hà uốn một sợi dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng 25 cm. Hỏi bác Hà cần bao nhiên mét dây thép?

A. 1 cm                 B. 100 cm

C. 1 m                   D. 100 m

Câu 7: Công thức tính diện tích hình bình hành là:

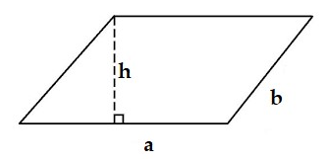
A. S = a . b            B. S = a . h  

C. S = b . h            D. S = a . b . h

Câu 8: Một đoàn khách du lịch gồm 52 người muốn qua sông nhưng mỗi thuyền chỉ chở được 6 người (kể cả người lái thuyền). Hỏi cần ít nhất bao nhiêu thuyền để chở hết số khách?

A. 9 thuyền           B. 10 thuyền

C. 11 thuyền         D. 12 thuyền

II. Phần tự luận (6 điểm)

Bài 1 (2 điểm):

1) Thực hiện các phép tính:

a) 25 . 8 – 15 . 5 + 160 : 16 – 10;

b) 2 . 5² – 3 : 71⁰ + 54 : 3³.

2) Phân tích các số 84, 120, 210 ra thừa số nguyên tố.

Bài 2 (1,5 điểm): Tính diện tích của phần được tô màu dưới đây biết: độ dài cạnh AB = 12 cm, BC = 4 cm và DG = 9 cm.

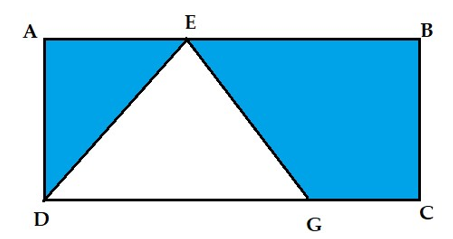
Bài 3 (2 điểm): Bạn Nguyên có 30 chiếc bánh dẻo và 40 chiếc bánh nướng. Bạn Nguyên muốn chia số bánh vào các hộp sao cho số bánh mỗi loại trong các hộp là như nhau. Hỏi số hộp bánh nhiều nhất bạn Nguyên chia được là bao nhiêu hộp?

Bài 4 (0,5 điểm): Tìm số tự nhiên n để 3n + 4 chia hết cho n – 1.

—

B. Đáp án và hướng dẫn giải

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: B	Câu 2: A	Câu 3: A	Câu 4: B
Câu 5: C	Câu 6: C	Câu 7: B	Câu 8: C

Hướng dẫn chi tiết

Câu 1:

Các số tự nhiên x thỏa mãn 4 < x ≤ 9 hay x lớn hơn 4 và nhỏ hơn hoặc bằng 9 là: 5, 6, 7, 8, 9.

Ta viết tập hợp A bằng cách liệt kê các phần tử ta được: A = {5; 6; 7; 8; 9}.

Ta viết tập hợp A bằng cách nêu dấu hiệu đặc trưng: A = {x \( \in \mathbb{N}\)| 4 < x ≤ 9}.

Chọn đáp án B.

Câu 2:

Sử dụng sàng Eratosthenes ta đã biết các số nguyên tố nhỏ hơn 25 là: 2, 3, 5, 7, 11, 13, 17, 19, 23.

Vậy có 9 số nguyên tố nhỏ hơn 25.

Chọn đáp án A.

Câu 3:

Quan sát hình vẽ: (đây là sơ đồ Ven)

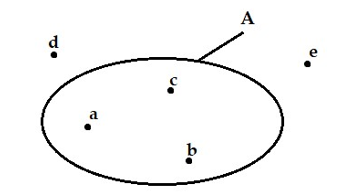
Ta thấy

+ Các phần tử a, b, c nằm trong vòng kín biểu diễn tập hợp A, nên các phần tử a, b, c đều thuộc tập hợp A, ta viết \(a \in A,b \in A,c \in A\).

+ Các phần tử d, e nằm ngoài vòng kín biểu diễn tập hợp A nên các phần tử này không thuộc tập hợp A, ta viết \(d \notin A,e \notin A.\)

Vậy đáp án A đúng.

Chọn đáp án A.

Câu 4:

Để tìm các ước của 16, ta lấy 16 lần lượt chia cho các số tự nhiên từ 1 đến 16, các phép chia hết là: 16 : 1 = 16, 16 : 2 = 8, 16 : 4 = 4, 16 : 8 = 2, 16 : 16 = 1.

Vậy các ước của 16 là: 1, 2, 4, 8, 16.

Ta viết tập hợp A các ước của 16 là A = {1; 2; 4; 8; 16}.

Chọn đáp án B.

Câu 5:

Hình vuông ABCD có các tính chất:

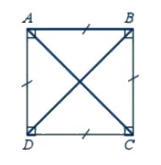
+ Bốn cạnh bằng nhau: AB = BC = CD = DA

+ Hai cạnh đối AB và CD, BC và AD song song với nhau

+ Hai đường chéo bằng nhau: AC = BD

+ Bốn góc ở các đỉnh A, B, C, D là góc vuông.

Vậy hình vuông đã cho không có tính chất AD và CD song song với nhau.

Chọn đáp án C.

Câu 6:

Số mét dây cần uốn chính là chu vi của hình thoi có độ dài cạnh bằng 25 cm và là:

P = 4 . 25 = 100 cm = 1 m

Vậy bác Hà cần 1 m dây thép để uốn.

Chọn đáp án C.

Câu 7:

Cho hình bình hành

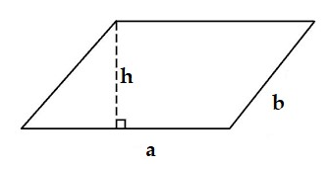
Diện tích của hình bình hành là S = a . h.

Chọn đáp án B.

Câu 8:

Vì mỗi thuyền chỉ chở được 6 người cả người lái đò nên mỗi thuyền chở được 5 người khách (trừ người lái đò).

Có tất cả 52 người khách. Ta thực hiện phép chia: 52 : 5 = 10 (dư 2)

Do đó dùng 10 thuyền để chở được 50 người khách và dư 2 người nên cần thêm một thuyền nữa để chở 2 người đó.

Vậy cần ít nhất 10 + 1 = 11 thuyền để chở hết số khách.

Chọn đáp án C.

II. Phần tự luận

Bài 1:

1)

a) 25 . 8 – 15 . 5 + 160 : 16 – 10

= 25 . 8 – 3 . 5 . 5 + 10 – 10

= 25 . 8 – 25 . 3 + (10 – 10)

= 25 . (8 – 3) + 0 = 25 . 5 = 125

b) 2 . 5² – 3 : 71⁰ + 54 : 3³ 

= 2 . 25 – 3 : 1 + 54 : 27

= 50 – 3 + 2

= 47 + 2 = 49

2)

Ta phân tích các số ra thừa số nguyên tố bằng cách viết theo cột dọc hoặc rẽ nhánh.

Vậy:

84 = 2 . 2 . 3 . 7 = 2² . 3 . 7

120 = 2 . 2 . 2 . 3 . 5 = 2³ . 3 . 5

210 = 2 . 3 . 5 . 7

Bài 2:

Diện tích hình chữ nhật ABCD là: AB . BC = 12 . 4 = 48 (cm²)

Diện tích hình tam giác DEG là: DG . BC : 2 = 9 . 4 : 2 = 18 (cm²) (đường cao xuất phát từ E của tam giác DEG có độ dài bằng BC)

Diện tích phần tô màu là: 48 – 18 = 30 (cm²)

                                      Đáp số: 30 cm².

Bài 3:

Gọi số hộp chia được là x (x là số tự nhiên khác 0)

Vì số bánh nướng trong mỗi hộp bằng nhau nên 40 ⁝ x.

Vì số bánh dẻo trong mỗi hộp bằng nhau nên 30 ⁝ x.

Vì x là số hộp bánh lớn nhất chia được nên x = ƯCLN(30, 40)

Ta có 30 = 2 . 3 . 5 và 40 = 2³ . 5 nên ƯCLN(30, 40) = 2 . 5 = 10

Hay x = 10 (thỏa mãn)

Vậy số hộp bánh chia được nhiều nhất là 10 hộp.

Bài 4:

Vì 3n + 4 = 3n + 7 – 3 = 3n – 3 + 7 = 3(n – 1) + 7

Do 3(n – 1) chia hết cho n – 1  (tính chất chia hết của một tích)

Nên để 3n + 4 chia hết cho n – 1 thì 7 phải chia hết cho n – 1 (tính chất chia hết của một tổng)

Hay (n – 1) thuộc Ư(7) = {1; 7}

Với n – 1 = 1 thì n = 2

Với n – 1 = 7 thì n = 8

Vậy với n = 2 hoặc n = 8 thì 3n + 4 chia hết cho n – 1.