65 câu Trắc nghiệm So sánh phân số. Hỗn số dương (Kết nối tri thức) có đáp án 2023 – Toán 6

Trắc nghiệm Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương

Phần 1. Trắc nghiệm So sánh phân số. Hỗn số dương

Dạng 1. So sánh phân số

Câu 1. Chọn câu đúng

A.$\frac{6}{7}<\frac{8}{7}<\frac{7}{7}$

B.$\frac{9}{22}<\frac{13}{22}<\frac{18}{22}$

C.$\frac{7}{15}<\frac{8}{15}<\frac{4}{15}$

D.$\frac{5}{11}>\frac{7}{11}>\frac{4}{11}$

Trả lời:

6 < 7 < 8 nên$\frac{6}{7}<\frac{7}{7}<\frac{8}{7}$

9 < 13 < 18 nên$\frac{9}{22}<\frac{13}{22}<\frac{18}{22}$

4 < 7 < 8 nên$\frac{4}{15}<\frac{7}{15}<\frac{8}{15}$

4 < 5 < 7 nên$\frac{4}{11}<\frac{5}{11}<\frac{7}{11}$

Đáp án cần chọn là: B

Câu 2. Chọn số thích hợp điền vào chỗ trống sau:$\frac{7}{23}<\frac{\mathrm{\dots }}{23}$

A. 9

B. 7

C. 5

D. 4

Trả lời:

7 < 9 nên$\frac{7}{23}<\frac{9}{23}$

Đáp án cần chọn là: A

Câu 3. Em hãy sắp xếp các phân số sau theo thứ tự giảm dần:$\frac{1}{4};\frac{2}{3};\frac{1}{2};\frac{4}{3};\frac{5}{2}$

A.$\frac{4}{3}>\frac{5}{2}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4};$

B.$\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4};$

C.$\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{4}>\frac{1}{2};$

D.$\frac{4}{3}>\frac{5}{2}>\frac{2}{3}>\frac{1}{4}>\frac{1}{2};$

Trả lời:

Ta có: các phân số có tử số nhỏ hơn mẫu số là các phân số nhỏ hơn1là:$\frac{1}{4};\frac{2}{3};\frac{1}{2}$

Quy đồng chung mẫu số các phân số này, ta được:$\frac{1}{4}=\frac{3}{12};\frac{2}{3}=\frac{8}{12};\frac{1}{2}=\frac{6}{12}$

Nhận thấy: $\frac{3}{12}<\frac{6}{12}<\frac{8}{12}$ suy ra$\frac{1}{4}<\frac{1}{2}<\frac{2}{3}$

Các phân số lớn hơn , nhỏ hơn là:

Phân số lớn hơn1nhỏ hơn2là:$\frac{4}{3}$

Phân số lớn hơn2là:$\frac{5}{2}$

Như vậy, sắp xếp các phân số theo thứ tự giảm dần là:$\frac{5}{2}>\frac{4}{3}>\frac{2}{3}>\frac{1}{2}>\frac{1}{4};$

Đáp án cần chọn là: B

Câu 4. Lớp 6A có$\frac{9}{35}$số học sinh thích bóng bàn,$\frac{3}{7}$số học sinh thích bóng chuyền,$\frac{4}{7}$số học sinh thích bóng đá. Môn bóng nào được các bạn học sinh lớp 6A yêu thích nhất?

A. Môn bóng bàn.

B. Môn bóng chuyền.

C. Môn bóng đá.

D. Cả 3 môn bóng được các bạn yêu thích như nhau.

Trả lời:

Ta có:

$\frac{3}{7}=\frac{15}{35};\frac{4}{7}=\frac{20}{35} \frac{9}{35}<\frac{15}{35}<\frac{20}{35}\frac{9}{35}<\frac{3}{7}<\frac{4}{7}$

Vậy môn bóng đá được các bạn lớp 6A yêu thích nhất.

Đáp án cần chọn là:C

Câu 5. Phân số$\frac{a}{b}$là phân số tối giản khi ƯC(a; b)bằng

A. {1; −1}

B. {2}

C. {1; 2}

D. {1; 2; 3}

Trả lời:

Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà cả tử và mẫu chỉ có ước chung là1 và−1.

Đáp án cần chọn là:A

Câu 6. Phân số nào dưới đây là phân số tối giản:

A.$\frac{-2}{4}$

B.$\frac{-15}{-96}$

C.$\frac{13}{27}$

D.$\frac{-29}{58}$

Trả lời:

Đáp án A:ƯCLN(2;4) = 2 ≠ 1 nên loại.

Đáp án B:ƯCLN(15;96) = 3 ≠ 1nên loại.

Đáp án C:ƯCLN(13;27) = 1 nên C đúng.

Đáp án D:ƯCLN(29;58) = 29 ≠ 1nên D sai.

Đáp án cần chọn là:C

Câu 7. Rút gọn phân số$\frac{\left(-2\right).3+6.5}{9.6}$về dạng phân số tối giản ta được phân số có tử số là

A.$\frac{4}{9}$

B. 31

C. −1

D. 4

Trả lời:

Ta có:$\frac{\left(-2\right).3+6.5}{9.6}=\frac{-6+30}{54}=\frac{24}{54}=\frac{24:6}{54:6}=\frac{4}{9}$

Vậy tử số của phân số cần tìm là4

Đáp án cần chọn là:D

Câu 8. Rút gọn phân số $\frac{4.8}{64.\left(-7\right)}$ta được phân số tối giản là:

A.$\frac{-1}{7}$

B.$\frac{-1}{14}$

C.$\frac{4}{-56}$

D.$\frac{-1}{70}$

Trả lời:

Ta có:$\frac{4.8}{64.\left(-7\right)}=\frac{4.8}{\mathrm{2.4.8.}\left(-7\right)}=\frac{1}{2.\left(-7\right)}=\frac{-1}{14}$

Đáp án cần chọn là: B

Câu 9. Phân số nào sau đây là kết quả của biểu thức $\frac{\mathrm{2.9.52}}{22.\left(-72\right)}$sau khi rút gọn đến tối giản?

A.$\frac{-13}{22}$

B.$\frac{13}{22}$

C.$\frac{13}{18}$

D.$\frac{-117}{198}$

Trả lời:

$\frac{\mathrm{2.9.52}}{22.\left(-72\right)}=\frac{{2.3}^2{.2}^2.13}{\mathrm{2.11.}\left(-2^3{.3}^2\right)}=\frac{2^3{.3}^2.13}{-2^4{.3}^{2}11}=\frac{13}{-2.11}=\frac{-13}{22}$

Đáp án cần chọn là: A

Câu 10. Điền dấu thích hợp vào chỗ chấm:$\frac{-5}{13}\mathrm{\dots }\frac{-7}{13}$

A. >

B. <

C. =

D. Tất cả các đáp án trên đều sai

Trả lời:

Vì -5 > – 7 nên$\frac{-5}{13}>\frac{-7}{13}$

Đáp án cần chọn là: A

Câu 11. Điền dấu thích hợp vào chỗ chấm:$\frac{-12}{23}\mathrm{\dots }\frac{-8}{23}$

A. >

B. <

C. =

D. Tất cả các đáp án trên đều sai

Trả lời:

Vì – 12 < – 8 nên$\frac{-12}{23}<\frac{-8}{23}$

Đáp án cần chọn là: B

Câu 12. Quy đồng mẫu số hai phân số $\frac{2}{7};\frac{5}{-8}$được hai phân số lần lượt là:

A.$\frac{16}{56};\frac{-35}{56}$

B.$\frac{16}{56};\frac{35}{56}$

C.$\frac{16}{56};\frac{35}{-56}$

D.$\frac{-16}{56};\frac{-35}{56}$

Trả lời:

Ta quy đồng$\frac{2}{7}$ và$\frac{-5}{8}$ (MSC: 56)

Đáp án cần chọn là: A

Câu 13. Quy đồng mẫu số các phân số $\frac{11}{12};\frac{15}{16};\frac{23}{20}$ta được các phân số lần lượt là:

A.$\frac{220}{240};\frac{225}{240};\frac{276}{240}$

B.$\frac{225}{240};\frac{220}{240};\frac{276}{240}$

C.$\frac{225}{240};\frac{276}{240};\frac{220}{240}$

D.$\frac{220}{240};\frac{276}{240};\frac{225}{240}$

Trả lời:

Ta có:$12=2^2.3;16=2^4;20=2^2.5$

Do đó$MSC=2^4\mathrm{.3.5}=240$

$\frac{11}{12}=\frac{11.20}{12.20}=\frac{220}{240}$

$\frac{15}{16}=\frac{15.15}{16.15}=\frac{225}{240}\frac{23}{20}=\frac{23.12}{20.12}=\frac{276}{240}$

Vậy các phân số sau khi đồng quy lần lượt là:$\frac{220}{240};\frac{225}{240};\frac{276}{240}$

Đáp án cần chọn là: A

Câu 14. Quy đồng mẫu số các phân số $\frac{7}{30};\frac{13}{60};\frac{-9}{40}$ta được các phân số lần lượt là:

A.$\frac{26}{120};\frac{27}{120};\frac{13}{120}$

B.$\frac{28}{120};\frac{26}{120};\frac{-27}{120}$

C.$\frac{28}{120};\frac{-27}{120};\frac{26}{120}$

D.$\frac{-28}{120};\frac{-13}{120};\frac{27}{120}$

Trả lời:

Ta có:

MSC = 120

$\frac{7}{30}=\frac{7.4}{30.4}=\frac{28}{120};$$\frac{13}{60}=\frac{13.2}{60.2}=\frac{26}{120};\frac{-9}{40}=\frac{-9.3}{40.3}=\frac{-27}{120}$

Vậy các phân số sau khi quy đồng lần lượt là:$\frac{28}{120};\frac{26}{120};\frac{-27}{120}$

Đáp án cần chọn là: B

Câu 15. Chọn câu đúng

A.$\frac{1123}{1125}>1$

B.$\frac{-154}{-156}<1$

C.$\frac{-123}{345}>0$

D.$\frac{-657}{-324}<0$

Trả lời:

Đáp án A: Vì 1123 < 1125 nên$\frac{1123}{1125}<1$

→ A sai.

Đáp án B: Vì 154 < 156 nên$\frac{-154}{-156}<1$

→ B đúng

Đáp án C: Vì$\frac{-123}{345}<0$ do nó là phân số âm

→ C sai.

Đáp án D:$\frac{-657}{-324}>0$ vì nó là phân số dương

→ D sai.

Đáp án cần chọn là: B

Câu 16. Sắp xếp các phân số $\frac{29}{40};\frac{28}{41};\frac{29}{41}$theo thứ tự tăng dần ta được

A.$\frac{29}{41};\frac{28}{41};\frac{29}{40}$

B.$\frac{29}{40};\frac{29}{41};\frac{28}{41}$

C.$\frac{28}{41};\frac{29}{41};\frac{29}{40}$

D.$\frac{28}{41};\frac{29}{40};\frac{29}{41}$

Trả lời:

Ta có:

+ 28 < 29 nên$\frac{28}{41}<\frac{29}{41}$

+ 41 > 40 nên$\frac{29}{41}<\frac{29}{40}$

Do đó:

Đáp án cần chọn là: C

Câu 17. Chọn câu đúng:

A.$\frac{11}{12}<\frac{-22}{12}$

B.$\frac{8}{3}<\frac{-9}{3}$

C.$\frac{7}{8}<\frac{9}{8}$

D.$\frac{6}{5}<\frac{4}{5}$

Trả lời:

11 > (-22) nên$\frac{11}{12}>\frac{-22}{12}$

8 > (-9) nên$\frac{8}{3}<\frac{-9}{3}$

7 < 9 nên$\frac{7}{8}<\frac{9}{8}$

6 > 4 nên$\frac{6}{5}>\frac{4}{5}$

Đáp án cần chọn là: C

Dạng 2. Các dạng toán về so sánh phân số

Câu 1. So sánh $A=\frac{2^5.7+2^5}{2^5{.5}^2-2^5.3}$và $\frac{3^4.5-3^6}{3^4.13+3^4}$với 1

A. A < 1 < B

B. A = B = 1

C. A > 1 > B

D. 1 > A > B

Trả lời:

$\frac{2^5.7+2^5}{2^5{.5}^2-2^5.3}=\frac{2^5.\left(7+1\right)}{2^5.\left(5^2-3\right)}=\frac{2^5.\left(7+1\right)}{2^5.\left(25-3\right)}=\frac{2^5.8}{2^5.22}=\frac{8}{22}=\frac{4}{11}$

$\frac{3^4.5-3^6}{3^4.13+3^4}=\frac{3^4.\left(5-3^2\right)}{3^4.\left(13+1\right)}=\frac{3^4.\left(5-9\right)}{3^4.\left(13+1\right)}=\frac{3^4.\left(-4\right)}{3^4.14}=\frac{-4}{14}=\frac{-2}{7}$

MSC = 77

$\frac{4}{11}=\frac{4.7}{11.7}=\frac{28}{77};\frac{-2}{7}=\frac{-2.11}{7.11}=\frac{-22}{77}$

Do đó: $\frac{-22}{77}<\frac{28}{77}<1$hay B < A < 1

Đáp án cần chọn là: D

Câu 2. Quy đồng mẫu hai phân số $\frac{3}{4}$ và$\frac{4}{5}$ ta được kết quả là:

A. $\frac{5}{20}$ và$\frac{25}{20}$

B. $\frac{15}{20}$ và$\frac{16}{20}$

C. $\frac{5}{4}$ và$\frac{2}{3}$

D. $\frac{1}{2}$ và$\frac{3}{2}$

Trả lời:

Để quy đồng mẫu hai phân số$\frac{3}{4}$và $\frac{4}{5}$, ta làm như sau:

– Tìm mẫu chung: BCNN(4, 5) = 20;

– Tìm thừa số phụ: 20 : 4 = 5 và 20 : 5 = 4;

– Ta có:$\frac{3}{4}=\frac{3.5}{4.5}=\frac{15}{20}$ và$\frac{4}{5}=\frac{4.4}{5.4}=\frac{16}{20}$

Đáp án cần chọn là:B

Câu 3. Chọn câu đúng:

A.$\frac{10}{11}>\frac{14}{5}$

B.$\frac{8}{13}>\frac{5}{2}$

C.$\frac{7}{5}>\frac{7}{8}$

D.$\frac{1}{5}>\frac{2}{3}$

Trả lời:

Ta có:

$\frac{10}{11}=\frac{50}{55};\frac{14}{5}=\frac{154}{55}$Vì$\frac{50}{55}<\frac{154}{55}\Rightarrow \frac{10}{11}<\frac{14}{5}$

$\frac{8}{13}=\frac{16}{26};\frac{5}{2}=\frac{65}{26}$ Vì$\frac{16}{26}<\frac{65}{26}\Rightarrow \frac{8}{13}<\frac{5}{2}$

$\frac{7}{5}=\frac{56}{40};\frac{7}{8}=\frac{35}{40}$ Vì$\frac{56}{40}>\frac{35}{40}\Rightarrow \frac{7}{5}>\frac{7}{8}$

$\frac{1}{5}=\frac{3}{15};\frac{2}{3}=\frac{10}{15}$ Vì$\frac{3}{15}<\frac{10}{15}\Rightarrow \frac{1}{5}<\frac{2}{3}$

Đáp án cần chọn là: C

Câu 4. Chọn số thích hợp điền vào chỗ trống sau:$\frac{7}{23}<\frac{\mathrm{\dots }}{23}$

A. 9

B. 7

C. 5

D. 4

Trả lời:

7 < 9 nên$\frac{7}{23}<\frac{9}{23}$

Đáp án cần chọn là: A

Câu 5. Chọn số thích hợp điền vào chỗ trống sau:$\frac{17}{19}<\frac{\mathrm{\dots }}{19}<1$

A. 16

B. 17

C. 18

D. 19

Trả lời:

Ta có:$1=\frac{19}{19}$

17 < 18 < 19 nên $\frac{17}{19}<\frac{18}{19}<\frac{19}{19}$ hay$\frac{17}{19}<\frac{18}{19}<1$

Đáp án cần chọn là: C

Câu 6. Khi quy đồng mẫu số, em hãy so sánh $\frac{34}{111}$và$\frac{198}{54}$

A.$\frac{34}{111}<\frac{198}{54}$

B.$\frac{34}{111}>\frac{198}{54}$

C.$\frac{34}{111}\ge \frac{198}{54}$

D.$\frac{34}{111}=\frac{198}{54}$

Trả lời:

Ta có:$\frac{34}{111}<1;\frac{198}{54}>1$

Do vậy:$\frac{34}{111}<\frac{198}{54}$

Đáp án cần chọn là: A

Câu 7. Lớp 6B gồm 35 học sinh có tổng chiều cao là 525 dm. Lớp 6B gồm 30 học sinh có tổng chiều cao là 456 dm. Nhận xét nào sau đây là đúng khi nói về chiều cao trung bình của các học sinh ở 2 lớp?

A. Chiều cao trung bình của các học sinh ở lớp 6A lớn hơn lớp 6B.

B. Chiều cao trung bình của các học sinh lớp 6B lớn hơn lớp 6A.

C. Chiều cao trung bình của các học sinh ở hai lớp bằng nhau.

D. Chưa đủ dữ liệu để so sánh chiều cao trung bình của học sinh ở hai lớp.

Trả lời:

Chiều cao trung bình của các học sinh ở lớp 6A là:$\frac{525}{35}$

Chiều cao trung bình của các học sinh ở lớp 6B là:$\frac{456}{30}$

Ta có:

Vì$\frac{75}{5}<\frac{76}{5}$ nên$\frac{525}{35}<\frac{456}{30}$

Vậy chiều cao trung bình của các học sinh lớp 6B lớn hơn lớp 6A.

Đáp án cần chọn là:B

Câu 8. Phân số nào dưới đây là kết quả của biểu thức $\frac{\mathrm{2.9.52}}{22.\left(-72\right)}$sau khi rút gọn đến tối giản?

A.$\frac{-13}{22}$

B.$\frac{13}{22}$

C.$\frac{-13}{18}$

D.$\frac{-117}{198}$

Trả lời:

$\frac{\mathrm{2.9.52}}{22.\left(-72\right)}=\frac{{2.3}^2{.2}^2.13}{\mathrm{2.11.}\left(-2^3{.3}^2\right)}=\frac{2^3{.3}^2.13}{-2^4{.3}^2.11}=\frac{13}{-2.11}=\frac{-13}{22}$

Đáp án cần chọn là: A

Câu 9. Biểu thức $\frac{5^{12}{.3}^9-5^{10}{.3}^{11}}{5^{10}{.3}^{10}}$sau khi đã rút gọn đến tối giản có mẫu số dương là:

A. 16

B. 3

C.$\frac{16}{5}$

D.$\frac{16}{3}$

Trả lời:

$\frac{5^{12}{.3}^9-5^{10}{.3}^{11}}{5^{10}{.3}^{10}}=\frac{5^{10}{.3}^9.\left(5^2-3^2\right)}{5^{10}{.3}^{10}}=\frac{5^{10}{.3}^9.16}{5^{10}{.3}^{10}}=\frac{16}{3}$

Vậy mẫu số của phân số đó là3

Đáp án cần chọn là:B

Câu 10. Sau khi rút gọn biểu thức $\frac{5^{11}{.7}^{12}+5^{11}{.7}^{11}}{5^{12}{.7}^{12}+{9.5}^{11}{.7}^{11}}$ta được phân số $\frac{a}{b}$.

Tính tổng a + b

A. 26

B. 13

C. 52

D. 8

Trả lời:

$\frac{5^{11}{.7}^{12}+5^{11}{.7}^{11}}{5^{12}{.7}^{12}+{9.5}^{11}{.7}^{11}}=\frac{5^{11}{.7}^{11}\left(7+1\right)}{5^{11}{.7}^{11}\left(5.7+9\right)}=\frac{8}{44}=\frac{2}{11}$

Do đó a = 2, b = 11 nên a + b = 13

Đáp án cần chọn là: B

Câu 11. Rút gọn phân số $\frac{9^{14}{.25}^5{.8}^7}{{18}^{12}{.625}^3{.24}^3}$ta được

A.$\frac{9}{5}$

B.$\frac{9}{25}$

C.$\frac{3}{25}$

D.$\frac{3}{5}$

Trả lời:

$\frac{9^{14}{.25}^5{.8}^7}{{18}^{12}{.625}^3{.24}^3}=\frac{{\left(3^2\right)}^{14}.{\left(5^2\right)}^5.{\left(2^3\right)}^7}{{\left({2.3}^2\right)}^{12}.{\left(5^4\right)}^3.{\left(2^3.3\right)}^3}=\frac{3^{28}{.5}^{10}{.2}^{21}}{2^{12}{.3}^{24}{.5}^{12}{.2}^9{.3}^3}$

$\frac{2^{21}{.3}^{28}{.5}^{10}}{2^{21}{.3}^{27}{.5}^{12}}=\frac{3}{5^2}=\frac{3}{25}$

Đáp án cần chọn là: C

Câu 12. Tìm phân số tối giản $\frac{a}{b}$ biết rằng lấy tử số cộng với 6, lấy mẫu số cộng với 14 thì ta được phân số bằng$\frac{3}{7}$

A.$\frac{4}{5}$

B $\frac{7}{3}$

C.$\frac{3}{7}$

D.$\frac{-3}{7}$

Trả lời:

Ta có:

$\frac{a+6}{b+14}=\frac{3}{7}$

7.(a + 6) = 3.(b + 14)

7a + 42 = 3b + 42

7a = 3b

$\frac{a}{b}=\frac{3}{7}$

Đáp án cần chọn là: C

Câu 13. Rút gọn phân số $\frac{-12a}{24},a\in Z$ta được:

A.$\frac{a}{2}$

B.$\frac{1}{2}$

C.$\frac{-1}{2}$

D.$\frac{-a}{2}$

Trả lời:

Ta có:$\frac{-12a}{24}=\frac{\left(-1\right)\mathrm{.12.}a}{12.2}=\frac{\left(-1\right).a}{2}=\frac{-a}{2}$

Đáp án cần chọn là: D

Câu 14. Rút gọn phân số $\frac{4.8}{64.\left(-7\right)}$ta được phân số tối giản là:

A.$\frac{-1}{7}$

B.$\frac{-1}{14}$

C.$\frac{4}{-56}$

D.$\frac{-1}{70}$

Trả lời:

Ta có:$\frac{4.8}{64.\left(-7\right)}=\frac{4.8}{\mathrm{2.4.8.}\left(-7\right)}=\frac{1}{2.\left(-7\right)}=\frac{-1}{14}$

Đáp án cần chọn là: B

Câu 15. Điền dấu thích hợp vào chỗ chấm:$\frac{-12}{25}\mathrm{\dots }\frac{17}{-25}$

A. >

B. <

C. =

D. Tất cả các đáp án trên đều sai

Trả lời:

$\frac{17}{-25}=\frac{-17}{25}$

Vì – 12 > – 17 nên $\frac{-12}{25}>\frac{-17}{25}$ hay$\frac{-12}{25}>\frac{17}{-25}$

Đáp án cần chọn là: A

Câu 16. Mẫu số chung của các phân số$\frac{2}{5};\frac{23}{18};\frac{5}{75}$ là

A. 180

B. 500

C. 750

D. 450

Trả lời:

Ta có:

5 = 5.1$3^2{.7}^2\mathrm{.11.19}$

18 = 2.3²

75 = 3.5²

⇒BCNN(5; 18; 75) = 2.3².5² = 450

Vậy ta có thể chọn một mẫu chung là450

Đáp án cần chọn là:D

Câu 17. Mẫu chung nguyên dương nhỏ nhất của các phân số$\frac{19}{3^2\mathrm{.7.11}};\frac{23}{3^3{.7}^2.19}$

A.$3^3{.7}^2$

B.$3^3{.7}^3\mathrm{.11.19}$

C.$3^2{.7}^2\mathrm{.11.19}$

D.$3^3{.7}^2\mathrm{.11.19}$

Trả lời:

BCNNhay mẫu chung nguyên dương nhỏ nhất của hai mẫu đã cho là$3^3{.7}^2\mathrm{.11.19}$

Đáp án cần chọn là:D

Câu 18. Chọn câu sai

A.$\frac{2}{-3}>\frac{-7}{8}$

B.$\frac{-22}{33}=\frac{200}{-300}$

C.$-\frac{2}{5}<\frac{196}{294}$

D.$\frac{-3}{5}<\frac{39}{-65}$

Trả lời:

Đáp án A: Ta có:

$\frac{2}{-3}=\frac{-2}{3}=\frac{-2.8}{3.8}=\frac{-16}{24}\frac{-7}{8}=\frac{-7.3}{8.3}=\frac{-21}{24}$

Vì $\frac{-16}{24}>\frac{-21}{24}$nên suy ra $\frac{2}{-3}>\frac{-7}{8}$nên A đúng

Đáp án B: Ta có:

$\frac{-22}{33}=\frac{-22:11}{33:11}=\frac{-2}{3}\frac{200}{-300}=\frac{-200}{300}=\frac{-200:100}{300:100}=\frac{-2}{3}$

Vì $\frac{-2}{3}=\frac{-2}{3}$nên suy ra $\frac{-22}{33}=\frac{200}{-300}$nên B đúng

Đáp án C: Ta có:

$-\frac{2}{5}<0;\frac{196}{294}>0\Rightarrow -\frac{2}{5}<0<\frac{196}{294}$

$\Rightarrow -\frac{2}{5}<\frac{196}{294}$nên C đúng

Đáp án D: Ta có:$\frac{39}{-65}=\frac{39:\left(-13\right)}{\left(-65\right):\left(-13\right)}=\frac{-3}{5}$

Vì $\frac{-3}{5}=\frac{-3}{5}\Rightarrow \frac{-3}{5}=\frac{39}{-65}$nên D sai

Đáp án cần chọn là: D

Câu 19. Sắp xếp các phân số $\frac{-3}{4};\frac{1}{12};\frac{-156}{149}$theo thứ tự giảm dần ta được:

A.$\frac{-156}{149};\frac{-3}{4};\frac{1}{12}$

B.$\frac{1}{12};\frac{-156}{149};\frac{-3}{4}$

C.$\frac{-3}{4};\frac{-156}{149};\frac{1}{12}$

D.$\frac{1}{12}\frac{-3}{4};\frac{-156}{149}$

Trả lời:

Dễ thấy:$\frac{-3}{4}<\frac{1}{12};\frac{-156}{149}<\frac{1}{12}$

So sánh: $\frac{-3}{4};$ và$\frac{-156}{149};$

Ta có:$\frac{-3}{4}=\frac{3}{-4}=\frac{3.52}{-4.52}=\frac{156}{-208};\frac{-156}{149}=\frac{156}{-149}$

Vì – 208 < – 149 nên $\frac{156}{-208}>\frac{156}{-149}$ hay$\frac{-3}{4}>\frac{-156}{149}$

Vậy$\frac{1}{12}>\frac{-3}{4}>\frac{-156}{149}$

Đáp án cần chọn là: D

Câu 20. Rút gọn rồi quy đồng mẫu số các phân số $\frac{3.4-3.7}{6.5+9}$và $\frac{6.9-2.17}{63.3-119}$ta được

A.$\frac{-21}{91};\frac{26}{91}$

B.$\frac{-3}{13};\frac{2}{7}$

C.$\frac{21}{91};\frac{26}{91}$

D.$\frac{-21}{91};\frac{36}{91}$

Trả lời:

$\frac{3.4-3.7}{6.5+9}=\frac{12-21}{30+9}=\frac{-9}{39}=\frac{-3}{13}\frac{6.9-2.17}{63.3-119}=\frac{54-34}{189-119}=\frac{20}{70}=\frac{2}{7}$

MSC = 91

$\frac{-3}{13}=\frac{-3.7}{13.7}=\frac{-21}{91};\frac{2}{7}=\frac{2.13}{7.13}=\frac{26}{91}$

Vậy sau khi quy đồng ta được hai phân số$\frac{-21}{91};\frac{26}{91}$

Đáp án cần chọn là: A

Câu 21. Cho $A=\frac{25.9-25.17}{-8.80-8.10}$ và$B=\frac{48.12-48.15}{-3.270-3.30}$ . Chọn câu đúng

A. A < B

B. A = B

C. A > 1; B < 0

D. A > B

Trả lời:

$A=\frac{25.9-25.17}{-8.80-8.10}=\frac{25.\left(9-17\right)}{-8.\left(80+10\right)}=\frac{25.\left(-8\right)}{\left(-8\right).90}=\frac{25}{90}=\frac{5}{18}B=\frac{48.12-48.15}{-3.270-3.30}=\frac{48.\left(12-15\right)}{\left(-3\right).\left(270+30\right)}=\frac{48.\left(-3\right)}{\left(-3\right).300}=\frac{48}{300}=\frac{4}{25}$

Vì A < 1 nên loại đáp án C

So sánh A và B:

MSC = 450

$\frac{5}{18}=\frac{5.25}{18.25}=\frac{125}{450};\frac{4}{25}=\frac{4.18}{25.18}=\frac{72}{450}$

Vì 125 > 72 nên $\frac{125}{450}>\frac{72}{450}$ hay$\frac{5}{18}>\frac{4}{25}$

Vậy A > B

Đáp án cần chọn là: D

Câu 22. Số các cặp số nguyên (x; y) thỏa mãn $\frac{1}{18}<\frac{x}{12}<\frac{y}{9}<\frac{1}{4}$là:

A. 2

B. 3

C. 1

D. 4

Trả lời:

MSC: 36

Khi đó:$\frac{1}{18}<\frac{x}{12}<\frac{y}{9}<\frac{1}{4}\Rightarrow \frac{2}{36}<\frac{x.3}{36}<\frac{y.4}{36}<\frac{9}{36}$

Mà $\left(x.3\right)⋮3;\left(y.4\right)⋮4$ nên$x.3\in \left\{3;6\right\};y.4\in \left\{4;8\right\}$

Màx.3 < y.4 nên:

+ Nếux.3 = 3 thìy.4 = 4hoặcy.4 = 8

Hay nếux = 1thìy = 1hoặcy = 2

+ Nếux.3 = 6thìy.4 = 8

Hay nếux = 2thìy = 2

Vậy các cặp số nguyên(x; y)là(1; 1), (1; 2), (2; 2)

Đáp án cần chọn là:B

Câu 23. Có bao nhiêu phân số lớn hơn$\frac{1}{6}$ nhưng nhỏ hơn$\frac{1}{4}$ mà có tử số là5.

A. 9

B. 10

C. 11

D. 12

Trả lời:

Gọi phân số cần tìm là$\frac{1}{x}\left(x\in N*\right)$

Ta có:$\frac{1}{6}<\frac{5}{x}<\frac{1}{4}$$\Rightarrow \frac{5}{30}<\frac{5}{x}<\frac{5}{20}\Rightarrow 30>x>20$

hay$x\in \left\{21;22;\mathrm{\dots };29\right\}$

Số giá trị củaxlà:(29−21):1+1=9

Vậy có tất cả9phân số thỏa mãn bài toán.

Đáp án cần chọn là:A

Câu 24. Tìm một phân số có mẫu là13, biết rằng giá trị của nó không thay đổi khi ta cộng tử với−20và nhân mẫu với5.

A.$\frac{10}{13}$

B.$\frac{7}{13}$

C.$\frac{-5}{13}$

D.$\frac{-10}{13}$

Trả lời:

Gọi phân số cần tìm là:$\frac{a}{13}\left(a\in Z\right)$

Theo yêu cầu bài toán:

$\frac{a}{13}=\frac{a+\left(-20\right)}{13.5}\frac{a.5}{13.5}=\frac{a+\left(-20\right)}{13.5}$

a.5 = a + (−20)

a.5 – a = −20

a.4 = −20

a = (−20):4

a = −5

Vậy phân số cần tìm là$\frac{-5}{13}$

Đáp án cần chọn là:C

Câu 25. So sánh các phân số$A=\frac{3535.232323}{353535.2323};B=\frac{3535}{3534};C=\frac{2323}{2322}$

A. A < B < C

B. A = B < C

C. A > B > C

D. A = B = C

Trả lời:

$A=\frac{3535.232323}{353535.2323}=\frac{\left(35.101\right).\left(23.10101\right)}{\left(35.10101\right).\left(23.101\right)}=1;B=\frac{3535}{3534}=\frac{3534+1}{3534}=\frac{3534}{3534}+\frac{1}{3534}=1+\frac{1}{3534};C=\frac{2323}{2322}=\frac{2322+1}{2322}=\frac{2322}{2322}+\frac{1}{2322}=1+\frac{1}{2322};$

Vì $\frac{1}{3534}<\frac{1}{2322}$nên B < C

Mà B > 1 nên B > A

Vậy A < B< C

Đáp án cần chọn là: A

Câu 26. So sánh$A=\frac{{2018}^{2018}+1}{{2018}^{2019}+1}$ và$B=\frac{{2018}^{2017}+1}{{2018}^{2018}+1}$

A. A < B

B. A = B

C. A > B

D. Không kết luận được

Trả lời:

Dễ thấy A < 1 nên:

$A=\frac{{2018}^{2018}+1}{{2018}^{2019}+1}<\frac{\left({2018}^{2018}+1\right)+2017}{\left({2018}^{2019}+1\right)+2017}$$=\frac{{2018}^{2018}+2018}{{2018}^{2019}+2018}=\frac{2018.\left({2018}^{2017}+1\right)}{2018.\left({2018}^{2018}+1\right)}$

$=\frac{{2018}^{2017}+1}{{2018}^{2018}+1}=B$

Vậy A < B

Đáp án cần chọn là: A

Dạng 3. Hỗn số dương

Câu 1. Viết các phân số và hỗn số sau dưới dạng số thập phân:
$\frac{-9}{1000}=\mathrm{\dots };\frac{-5}{8}=\mathrm{\dots };3\frac{2}{25}=\mathrm{\dots }$

A. −0,09; −0,625; 3,08

B. −0,009; −0,625; 3,08

C. −0,9; −0,625; 3,08

D. −0,009; −0,625; 3,008

Trả lời:

$\frac{-9}{1000}=-\mathrm{0,009}$

$\frac{-5}{8}=\frac{-5.125}{8.125}=\frac{-625}{1000}=-\mathrm{0,625}$

$3\frac{2}{25}=3\frac{8}{100}=\mathrm{3,08}$

Đáp án cần chọn là: B

Câu 2. Viết các số thập phân sau dưới dạng phân số tối giản:

– 0,125 = …; – 0,012 = …; – 4,005 = …

A.$\frac{-1}{8};\frac{-3}{250};\frac{-4005}{1000}$

B.$\frac{-1}{8};\frac{-3}{25};\frac{-801}{200}$

C.$\frac{-1}{4};\frac{-3}{250};\frac{-801}{200}$

D.$\frac{-1}{8};\frac{-3}{250};\frac{-801}{200}$

Trả lời:

$-\mathrm{0,125}=\frac{-125}{1000}=\frac{-125:125}{1000:125}=\frac{-1}{8}-\mathrm{0,012}=\frac{-12}{1000}=\frac{-12:4}{1000:4}=\frac{-3}{250}-\mathrm{4,005}=\frac{-4005}{1000}=\frac{-4005:5}{1000:5}=\frac{-801}{200}$

Đáp án cần chọn là: D

Câu 3. Tính giá trị biểu thức $M=60\frac{7}{13}.x+50\frac{8}{13}.x-11\frac{2}{13}.x$ biết$x=-8\frac{7}{10}$

A. – 870

B. – 87

C. 870

D.$92\frac{7}{10}$

Trả lời:

$M=60\frac{7}{13}.x+50\frac{8}{13}.x-11\frac{2}{13}.xM=\left(60\frac{7}{13}+50\frac{8}{13}-11\frac{2}{13}\right).xM=\left[\left(60+50-11\right)+\left(\frac{7}{13}+\frac{8}{13}-\frac{2}{13}\right)\right].xM=\left(99+1\right).x=100x$

Thay $x=-8\frac{7}{10}$vào M ta được:

$M=100.\left(-8\frac{7}{10}\right)=100.\left(-\frac{87}{10}\right)=-870$

Đáp án cần chọn là: A

Câu 4. Tìm số tự nhiên x sao cho:$6\frac{1}{3}:4\frac{2}{9}<x<\left(10\frac{2}{9}+2\frac{2}{5}\right)-6\frac{2}{9}$

A.$x\in \left\{2;3;4;5;6\right\}$

B.$x\in \left\{3;4;5;6\right\}$

C.$x\in \left\{2;3;4;5\right\}$

D.$x\in \left\{3;4;5;6;7\right\}$

Trả lời:

$6\frac{1}{3}:4\frac{2}{9}<x<\left(10\frac{2}{9}+2\frac{2}{5}\right)-6\frac{2}{9}\frac{19}{3}:\frac{38}{9}<x<\frac{92}{9}+\frac{12}{5}-\frac{56}{9}\frac{3}{2}<x<\frac{32}{5}$

Ta có:

$\frac{3}{2}<x<\frac{32}{5}$

1,5 < x < 6,4

Vì x là số tự nhiên nên$x\in \left\{2;3;4;5;6\right\}$

Đáp án cần chọn là: A

Câu 5. Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:

a) 125 dm²; b) 218 cm²; c) 240 dm²; d)34 cm²

A.$1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{1000}{m}^2;\frac{17}{5000}{m}^2$

B.$1\frac{25}{100}{m}^2;2\frac{9}{50}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{5000}{m}^2$

C.$1\frac{25}{100}{m}^2;2\frac{9}{50}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{50}{m}^2$

D.$1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{50}{m}^2$

Trả lời:

a)$125d{m}^2=\frac{125}{100}{m}^2=1\frac{25}{100}{m}^2$

b)$218c{m}^2=\frac{218}{10000}{m}^2=\frac{109}{5000}{m}^2$

c)$240d{m}^2=\frac{240}{100}{m}^2=2\frac{40}{100}{m}^2$

d)$34c{m}^2=\frac{34}{10000}{m}^2=\frac{17}{5000}{m}^2$

Vậy ta được:$1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{1000}{m}^2;\frac{17}{5000}{m}^2$

Đáp án cần chọn là: A

Câu 6. Viết 2 giờ 15 phút dưới dạng hỗn số với đơn vị là giờ:

A.$1\frac{1}{4}$ giờ

B. $2\frac{1}{5}$giờ

C. $2\frac{1}{4}$giờ

D.$15\frac{1}{30}$ giờ

Trả lời:

2 giờ 15 phút = $2+\frac{15}{60}=2+\frac{1}{4}=2\frac{1}{4}$giờ

Đáp án cần chọn là: C

Câu 7. Viết phân số $\frac{4}{3}$dưới dạng hỗn số ta được:

A.$1\frac{2}{3}$

B.$3\frac{1}{3}$

C.$3\frac{1}{4}$

D.$1\frac{1}{3}$

Trả lời:

Ta có: 4 : 3 bằng a (dư 1) nên$\frac{4}{3}=1\frac{1}{3}$

Đáp án cần chọn là: D

Câu 8. Tính$\left(-2\frac{1}{4}\right)+\frac{5}{2}$

A.$-\frac{1}{4}$

B.$\frac{3}{2}$

C. $\frac{1}{4}$

D.$\frac{3}{4}$

Trả lời:

$\left(-2\frac{1}{4}\right)+\frac{5}{2}=-\frac{9}{4}+\frac{5}{2}=-\frac{9}{4}+\frac{10}{4}=\frac{1}{4}$

Đáp án cần chọn là: C

Câu 9. Tìm x biết$2\frac{x}{7}-=\frac{75}{35}$

A. x = 1

B. x = 2

C. x = 3

D. x = 4

Trả lời:

Ta có:

$2\frac{x}{7}=\frac{75}{35}\frac{2.7+x}{7}=\frac{15}{7}$

14 + x = 15

x = 15 – 14

x = 1

Đáp án cần chọn là: A

Câu 10. Chọn câu đúng

A.$\left(-3\frac{3}{4}\right).1\frac{1}{2}=-3\frac{3}{8}$

B.$3\frac{3}{4}:1\frac{1}{5}=3\frac{3}{20}$

C.$\left(-3\right)-\left(-2\frac{2}{5}\right)=\frac{-3}{5}$

D.$5\frac{7}{10}.15=\frac{105}{2}$

Trả lời:

Đáp án A:$\left(-3\frac{3}{4}\right).1\frac{1}{2}=-\frac{15}{4}.\frac{3}{2}=-\frac{45}{8}=-5\frac{5}{8}\ne -3\frac{3}{8}$

Nên A sai.

Đáp án B:$3\frac{3}{4}:1\frac{1}{5}=\frac{15}{4}:\frac{6}{5}=\frac{15}{4}.\frac{5}{6}=\frac{25}{8}=3\frac{1}{8}\ne 3\frac{3}{20}$

Nên B sai

Đáp án C:$\left(-3\right)-\left(-2\frac{2}{5}\right)=\left(-3\right)-\left(-\frac{12}{5}\right)=\left(-3\right)+\frac{12}{5}=\frac{-3}{5}$

Nên C đúng

Đáp án D:$5\frac{7}{10}.15=\frac{57}{10}.15=\frac{171}{2}\ne \frac{105}{2}$

Nên D sai

Đáp án cần chọn là: C

Câu 11. Dùng hỗn số viết thời gian ở đồng hồ trong các hình vẽ, ta được lần luwotj các hỗn số là:

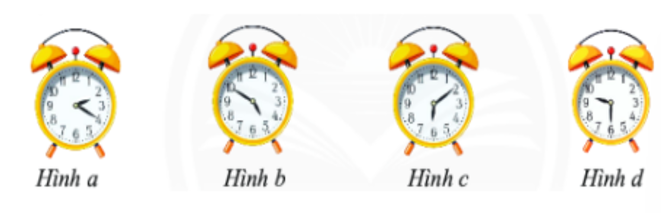
A.$2\frac{1}{3};4\frac{5}{6};6\frac{1}{6};9\frac{1}{2}$

B.$2\frac{1}{4};4\frac{1}{6};6\frac{1}{6};9\frac{1}{2}$

C.$2\frac{1}{3};4\frac{5}{6};6\frac{5}{6};9\frac{1}{2}$

D.$2\frac{1}{3};4\frac{5}{6};6\frac{1}{6};9\frac{1}{6}$

Trả lời:

Hình a:$2\frac{1}{3}$

Hình b:$4\frac{5}{6}$

Hình c:$6\frac{1}{6}$

Hình d:$9\frac{1}{2}$

Vậy ta được các hỗn số:$2\frac{1}{3};4\frac{5}{6};6\frac{1}{6};9\frac{1}{2}$

Đáp án cần chọn là: A

Dạng 4. Các dạng toán về hỗn số dương

Câu 1. Tính hợp lí $A=\left(4\frac{5}{17}-3\frac{4}{5}+8\frac{15}{29}\right)-\left(3\frac{5}{17}-6\frac{14}{29}\right)$ta được

A.$13\frac{4}{5}$

B.$12\frac{1}{5}$

C.$-3\frac{4}{5}$

D.$10\frac{4}{5}$

Trả lời:

$A=\left(4\frac{5}{17}-3\frac{4}{5}+8\frac{15}{29}\right)-\left(3\frac{5}{17}-6\frac{14}{29}\right)$

$A=4\frac{5}{17}-3\frac{4}{5}+8\frac{15}{29}-3\frac{5}{17}+6\frac{14}{29}A=\left(4\frac{5}{17}-3\frac{5}{17}\right)+\left(8\frac{15}{29}+6\frac{14}{29}\right)-3\frac{4}{5}A=\left(4-3\right)+\left(\frac{5}{17}-\frac{5}{17}\right)+\left(8+6\right)+\left(\frac{15}{29}+\frac{14}{29}\right)-3\frac{4}{5}A=1+0+14+1-3\frac{4}{5}A=16-3\frac{4}{5}A=15\frac{5}{5}-3\frac{4}{5}=12\frac{1}{5}$

Đáp án cần chọn là: B

Câu 2. Giá trị của $N=-\frac{1}{7}\left(9\frac{1}{2}-\mathrm{8,75}\right):\frac{2}{7}+\mathrm{0,625}:1\frac{2}{3}$là:

A.$-\frac{5}{6}$

B. 0

C.$-\frac{6}{5}$

D. 1

Trả lời:

$N=-\frac{1}{7}\left(9\frac{1}{2}-\mathrm{8,75}\right):\frac{2}{7}+\mathrm{0,625}:1\frac{2}{3}$

$N=-\frac{1}{7}\left(\frac{19}{2}-\frac{875}{100}\right).\frac{7}{2}+\frac{625}{1000}:\frac{5}{3}N=-\frac{1}{7}\left(\frac{19}{2}-\frac{35}{4}\right).\frac{7}{2}+\frac{5}{8}.\frac{3}{5}N=-\frac{1}{7}.\frac{3}{4}.\frac{7}{2}+\frac{3}{8}N=-\frac{3}{8}+\frac{3}{8}=0$

Đáp án cần chọn là: B

Câu 3. Tìm x biết$\frac{\left(\mathrm{1,16}-x\right)\mathrm{.5,25}}{\left(10\frac{5}{9}-7\frac{1}{4}\right).2\frac{2}{17}}=75\%$

A. 0

B.$\frac{6}{5}$

C.$\frac{4}{25}$

D. 1

Trả lời:

Đáp án cần chọn là: C

Câu 4. Sắp xếp các khối lượng sau theo thứ tự từ lớn đến nhỏ:

$3\frac{3}{4}$tạ; $\frac{377}{100}$tạ; $\frac{7}{2}$tạ; $3\frac{45}{100}$tạ; 365 kg

A. $3\frac{45}{100}$tạ; $\frac{7}{2}$tạ; 365 kg; $3\frac{3}{4}$tạ; $\frac{377}{100}$tạ;

B. $3\frac{3}{4}$tạ; $\frac{377}{100}$tạ; $\frac{7}{2}$tạ; $3\frac{45}{100}$tạ; 365 kg

C. $\frac{377}{100}$tạ; $3\frac{3}{4}$tạ; ; 365 kg; $\frac{7}{2}$tạ; $3\frac{45}{100}$tạ

D. $3\frac{3}{4}$tạ; 365 kg; $\frac{7}{2}$tạ; $3\frac{45}{100}$tạ; $\frac{377}{100}$tạ

Trả lời:

Ta có:

$3\frac{3}{4}$tạ = $\frac{15}{4}$tạ = $\frac{377}{100}$tạ

$\frac{7}{2}$tạ = $\frac{350}{100}$tạ

$3\frac{45}{100}$ tạ =$\frac{365}{100}$tạ

→ Các khối lượng theo thứ tự từ lớn đến nhỏ là:

$\frac{377}{100}$tạ; $3\frac{3}{4}$ tạ ; 365 kg; $\frac{7}{2}$tạ;$3\frac{45}{100}$tạ

Đáp án cần chọn là: C

Câu 5. Dùng phân số hoặc hỗn số (nếu có thể) để viết các đại lượng diện tích dưới đây theo mét vuông, ta được:

a) 125 dm²; b) 218 cm²; c) 240 dm²; d) 34 cm²

A. $1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{5000}{m}^2$

B.$1\frac{25}{100}{m}^2;2\frac{9}{50}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{5000}{m}^2$

C.$1\frac{25}{100}{m}^2;2\frac{9}{50}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{50}{m}^2$

D.$1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{50}{m}^2$

Trả lời:

a)$125d{m}^2=\frac{125}{100}{m}^2=1\frac{25}{100}{m}^2$

b)$218c{m}^2=\frac{218}{10000}{m}^2=\frac{109}{5000}{m}^2$

c)$240d{m}^2=\frac{240}{100}{m}^2=2\frac{40}{100}{m}^2$

d)$34c{m}^2=\frac{34}{10000}{m}^2=\frac{17}{5000}{m}^2$

Vậy ta được:$1\frac{25}{100}{m}^2;\frac{109}{5000}{m}^2;2\frac{40}{100}{m}^2;\frac{17}{5000}{m}^2$

Đáp án cần chọn là: A

Câu 6. Hai xe ô tô cùng đi được quãng đường 100 km, xe taxi chạy trong115115giờ và xe tải chạy trong 70 phút. So sánh vận tốc hai xe.

A. Vận tốc xe tải lớn hơn vận tốc xe taxi

B. Vận tốc xe taxi lớn hơn vận tốc xe tải

C. Vận tốc hai xe bằng nhau

D. Không so sánh được

Trả lời:

Đổi 70 phút = $\frac{7}{6}$giờ

Vận tốc của xe taxi là:$100:1\frac{1}{5}=100:\frac{6}{5}=\frac{250}{3}=83\frac{1}{3}\left(km/h\right)$

Vận tốc của xe tải là:$100:\frac{7}{5}=\frac{600}{7}=85\frac{5}{7}\left(km/h\right)$

Ta có: $85\frac{5}{7}>83\frac{1}{3}$nên vận tốc của xe taxi lớn hơn vận tốc xe tải

Đáp án cần chọn là: B

Câu 7. Hỗn số $-2\frac{3}{4}$được viết dưới dạng phân số là:

A.$-\frac{21}{4}$

B.$-\frac{11}{4}$

C.$-\frac{10}{4}$

D.$-\frac{5}{4}$

Trả lời:

$-2\frac{3}{4}=-\frac{2.4+3}{4}=-\frac{11}{4}$

Đáp án cần chọn là: B

Câu 8. Chọn câu đúng

A.$\frac{19.20}{19+20}=\frac{1}{19}+\frac{1}{20}$

B.$6\frac{23}{11}=\frac{6.23+11}{11}$

C.$a\frac{a}{99}=\frac{100a}{99}\left(a\in N*\right)$

D.$1\frac{15}{23}=\frac{1.23}{15}$

Trả lời:

Đáp án A:

$\frac{1}{19}+\frac{1}{20}=\frac{20}{19.20}+\frac{19}{19.20}=\frac{19+20}{19.20}\ne \frac{19.20}{19+20}$

Nên A sai

Đáp án B: $6\frac{23}{11}=\frac{6.11+23}{11}\ne \frac{6.23+11}{11}$nên B sai.

Đáp án C:$a\frac{a}{99}=\frac{a.99+a}{99}=\frac{a.\left(99+1\right)}{99}=\frac{100a}{99}$ nên C đúng.

Đáp án D: $1\frac{15}{23}=\frac{1.23+15}{15}\ne \frac{1.23}{15}$nên D sai.

Đáp án cần chọn là: C

Câu 9. Sắp xếp theo thứ tự tăng dần 23%;$\frac{12}{100};-1\frac{1}{12};-\frac{31}{24};5\frac{1}{2}$ ta được

A.$-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<5\frac{1}{2}<23\%$

B.$-\frac{31}{24}<-1\frac{1}{12}<23\%<\frac{12}{100}<5\frac{1}{2}$

C.$-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<23\%<5\frac{1}{2}$

D.$-1\frac{1}{12}<-\frac{31}{24}<\frac{12}{100}<23\%<5\frac{1}{2}$

Trả lời:

Ta có:$23\%=\frac{23}{100};-1\frac{1}{12}=-\frac{13}{12};5\frac{1}{2}=\frac{11}{2}$

Ta chia thành hai nhóm phân số là: $\frac{23}{100};\frac{12}{100};\frac{11}{2}$ và$-\frac{13}{12};-\frac{31}{24}$

Nhóm 1:$\frac{23}{100};\frac{12}{100};\frac{11}{2}$

$\frac{12}{100}<\frac{23}{100}<1<\frac{11}{2}$nên$\frac{12}{100}<\frac{23}{100}<\frac{11}{2}$

Nhóm 2:$-\frac{13}{12};-\frac{31}{24}$

$-\frac{13}{12}=-\frac{26}{24}>-\frac{31}{24}$ nên$-\frac{13}{12}>-\frac{31}{24}$

Vậy$-\frac{31}{24}<-\frac{13}{12}<\frac{12}{100}<\frac{23}{100}<\frac{11}{2}$

Hay$-\frac{31}{24}<-1\frac{1}{12}<\frac{12}{100}<23\%<5\frac{1}{2}$

Đáp án cần chọn là: C

Câu 10. Kết quả của phép tính $\left(-1\frac{1}{3}\right)+2\frac{1}{2}$bằng:

A.$\frac{11}{6}$

B.$\frac{7}{6}$

C.$\frac{13}{6}$

D.$-\frac{5}{6}$

Trả lời:

$\left(-1\frac{1}{3}\right)+2\frac{1}{2}=-\frac{4}{3}+\frac{5}{2}=\frac{-8}{6}+\frac{15}{6}=\frac{7}{6}$

Đáp án cần chọn là: B

Câu 11. Giá trị nào dưới đây của x thỏa mãn$x-3\frac{1}{2}x=-\frac{20}{7}$

A.$1\frac{1}{7}$

B.$1\frac{1}{7}$

C.$\frac{6}{7}$

D.$\frac{7}{8}$

Trả lời:

$x-3\frac{1}{2}x=-\frac{20}{7}$

$x-\frac{7}{2}x=-\frac{20}{7}$

$x\left(1-\frac{7}{2}\right)=-\frac{20}{7}$

$x.\left(\frac{-5}{2}\right)=-\frac{20}{7}$

$x=-\frac{20}{7}:\frac{-5}{2}$

$x=\frac{8}{7}$

$x=1\frac{1}{7}$

Đáp án cần chọn là: A

Phần 2. Lý thuyết So sánh phân số. Hỗn số dương

1. Quy đồng mẫu nhiều phân số

Để quy đồng hai hay nhiều phân số ta làm như sau:

Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.

Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Ví dụ 1: Để quy đồng ba phân số 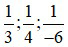 ta làm như sau:

+ Đưa về các phân số có mẫu dương:  .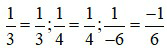

+ Tìm mẫu chung: BCNN (3; 4; 6) = 12

+ Thừa số phụ: 

12 : 3 = 4

12 : 4 = 3

12 : 6 = 2

Ta có: 

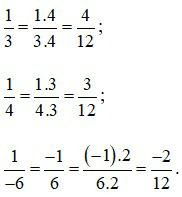
2. So sánh hai phân số

a) So sánh hai phân số cùng mẫu

– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Ví dụ 2: 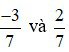  là hai phân số có cùng mẫu số dương.

Vì –3 < 2 nên  .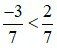

b) So sánh hai phân số không cùng mẫu

– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Ví dụ 3: So sánh hai phân số sau: .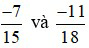

BCNN (15; 18) = 90

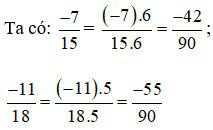
Vì –42 > –55 nên 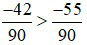 do đó,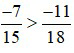 

3. Hỗn số dương

– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi 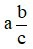 là một hỗn số dương với a là phần nguyên và  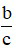là phần phân số.

Ví dụ 4: 

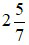 là một hỗn số dương với phần nguyên là 2 và phần phân số là 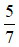. Khi đó ta đọc  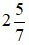là hai năm phần bảy.

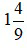 là một hỗn số dương với phần nguyên là 1 và phần phân số là  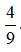. Khi đó ta đọc 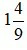 là một bốn phần chín.

– Muốn đổi từ hỗn số sang phân số ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số.

Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.

Ví dụ 5: Đổi hỗn số 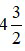 sang phân số:

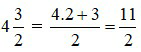
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.

Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.

Ví dụ 6: Đổi phân số 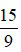 sang hỗn số

Ta có 15 chia 9 được thương là 1 và dư 6 do đó:

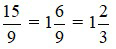
Xem thêm các bài Trắc nghiệm Toán 6 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 23: Mở rộng phân số. Phân số bằng nhau

Trắc nghiệm Bài 24: So sánh phân số. Hỗn số dương

Trắc nghiệm Bài 25: Phép cộng và phép trừ phân số

Trắc nghiệm Bài 26: Phép nhân và phép chia phân số

Trắc nghiệm Bài 27: Hai bài toán về phân số