25 câu Trắc nghiệm Bội chung. Bội chung nhỏ nhất (Chân trời sáng tạo) có đáp án 2023 – Toán 6

Trắc nghiệm Toán lớp 6 Bài 13: Bội chung. Bội chung nhỏ nhất

Phần 1. Trắc nghiệm Bội chung. Bội chung nhỏ nhất

Dạng 1. Bội chung. Bội chung nhỏ nhất

Câu 1. Mẫu số nhỏ nhất khi quy đồng các phân số $\frac{3}{16}$ và $\frac{5}{24}$ là

A. 24

B. 48

C. 96

D. 16

Trả lời:

Ta có: BCNN(16, 24) = 48

Mẫu chung nhỏ nhất khi quy đồng $\frac{3}{16}$ và $\frac{5}{24}$ là 48.

Đáp án cần chọn là: B

Câu 2. Chọn câu trả lời sai.

A. 5∈ ƯC(55;110)

B. 24∈BC(3;4)

C. 10∉ ƯC(55;110)

D. 12⊂BC(3;4)

Trả lời:

+) Ta thấy 55⁝5; 110⁝5 nên 5ϵ ƯC(55;110)

Do đó A đúng.

+) Vì 24⁝3; 24⁝4 nên 24ϵBC(3;4)

Do đó B đúng.

+) Vì 55 không chia hết cho 10 nên 10∉ ƯC(55;110)

Do đó C đúng.

+) Vì 12⁝3;12⁝4 nên 12ϵBC(3;4). Kí hiệu 12⊂BC(3;4) là sai.

Do đó D sai.

Đáp án cần chọn là: D

Câu 3. Choa∈BC(6; 8), vậy số a nhận giá trị nào sau đây:

A. 2

B. 12

C. 24

D. 36

Trả lời:

B(6) ={0,6,12,24…}

B(8) ={0,8,24,…}

BC(6,8) ={0,24,…}

Đáp án cần chọn là: C

Câu 4. Giao của tập của hai tập hợpA={toán, văn, thể dục, ca nhạc} và B={mỹ thuật, toán, văn, giáo dục công dân}

A. C ={toán, văn, thể dục}

B. C ={toán, văn}

C. C ={toán, văn, thể dục, ca nhạc}

D. C ={toán, thể dục, giáo dục công dân}

Trả lời:

Gọi C=A∩B

Vậy C={toán, văn}

Đáp án cần chọn là: B

Câu 5. BCNN(10, 15, 30) là:

A. 10

B. 15

C. 30

D. 60

Trả lời:

Ta có: 30 là bội của 10 và 15

=> BCNN(10, 15, 30) = 30.

Đáp án cần chọn là: C

Câu 6. Số x là bội chung của a; b; c nếu:

A. x⋮a hoặc x⋮b hoặc x⋮c

B. x⋮a và x⋮b

C. x⋮b và x⋮c

D. x⋮a và x⋮b và x⋮c

Trả lời:

Số x là bội chung của 3 số a, b, c nếu x chia hết cho cả a, b, c.

Đáp án cần chọn là: D

Câu 7. Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.

A. 0

B. 6

C. 2

D. 3

Trả lời:

B(2) ={0;2;4;6;8;…}

B(3) ={0;3;6;9;…}

Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.

Đáp án cần chọn là: B

Câu 8. Tìm BCNN(38,76)

A. 2888

B. 37

C. 76

D. 144

Trả lời:

Ta có 76⋮38 nên BCNN(38;76)=76.

Đáp án cần chọn là: C

Câu 9. Tìm bội chung nhỏ nhất của 9 và 15, biết 9 = 3²và 15 = 3. 5.

A. 15

B. 45

C. 90

D. 150

Trả lời:

Thừa số nguyên tố của 9 là 3

Thừa số nguyên tố của 15 là 3 và 5.

Các thừa số chung và riêng của 9 và 15 là 3 và 5.

Số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1.

BCNN(9, 15) = 3².5= 45

Đáp án cần chọn là: B

Câu 10. Quy đồng mẫu hai phân số $\frac{7}{9}$ và $\frac{4}{15}$ với mẫu số nhỏ nhất thì được các phân số lần lượt là:

A. $\frac{12}{45}$ và $\frac{35}{45}$

B. $\frac{35}{45}$ và $\frac{12}{45}$

C. $\frac{70}{90}$ và $\frac{24}{90}$

D. $\frac{45}{35}$ và $\frac{12}{35}$

Trả lời:

Ta có: BCNN (9, 15) – 45 nên:

$\frac{7}{9}=\frac{7.5}{9.5}=\frac{35}{45}\frac{4}{15}=\frac{4.3}{15.3}=\frac{12}{45}$

Đáp án cần chọn là: B

Dạng 2. Các dạng toán về bội chung, bội chung nhỏ nhất

Câu 1. Có bao nhiêu số tự nhiên x khác 0 thỏa mãn x∈BC(12;15;20) và x≤ 100

A. 4

B. 3

C. 2

D. 1

Trả lời:

Ta có B(12)={0;12;24;36;48;60;72;84;96;…}

B(15)={0;15;30;45;60;75;90;105;…}

B(20)={0;20;40;60;80;100;…}

Nên BC(12;15;20)={0;60;120;…} mà x≤100 và x≠0 nên x=60.

Có một số tự nhiên thỏa mãn đề bài.

Đáp án cần chọn là: D

Câu 2. Tìm số tự nhiên x nhỏ nhấtbiết x⁝45;x⁝110 và x⁝75

A. 1650

B. 3750

C. 4950

D. 3300

Trả lời:

Vì x⁝45;x⁝110 và x⁝75nên x ϵ BC(45;75;110) mà x nhỏ nhất nên

x = BCNN(45;75;110)

Ta có 45 = 3².5; 75 = 3.5²; 110 = 2.5.11

Nên BCNN(45;75;110) = 2.3².5².11 = 4950

Đáp án cần chọn là: C

Câu 3. Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác 0 của nó là 256.

A. 16

B. 18

C. 24

D. 32

Trả lời:

x⁝45; x⁝110 và x⁝75Gọi số cần tìm là a (a≠0)
Ước số lớn nhất của alà a
Bội số nhỏ nhất khác 0của alà a
Tích của ước số lớn nhất với bội số nhỏ nhất là:

a.a = 256 = 16²

⇒a = 16

Vậy số cần tìm là 16.

Đáp án cần chọn là: A

Câu 4. Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp 35 hay 40 học sinh lên một ô tô thì đều thấy thiếu mất 5 ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ 800 đến 900 em.

A. 845

B. 840

C. 860

D. 900

Trả lời:

Gọi số học sinh đi thăm quan là x(xϵ N*; 800 ≤ x ≤ 900) (học sinh)

Nếu xếp 35 hay 40 học sinh lên một ô tô thì đều thấy thiếu mất 5 ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có

(x−5)⁝35; (x−5)⁝40 suy ra (x−5) ϵ BC(35;40)

Ta có

35 = 5.7; 40 = 2³.5 nên

BCNN(35;40) = 2³.5.7 = 280.

Suy ra (x−5) ϵ BC(35;40) = B(280)

= {280;560;840;1120;…}

mà 800 ≤ x ≤ 900 nên x – 5 = 840 hay x = 845.

Vậy số học sinh đi thăm quan là 845 học sinh.

Đáp án cần chọn là: A

Câu 5. Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ 200 đến 300 bông.

A. 210

B. 220

C. 230

D. 240

Trả lời:

– Gọi số bông sen chị Hòa có là: x (bông, xN).

– Nếu chị bó thành các bỏ bông gồm 3 bông, 5 bông hay 7 bông thì số bông sen chị Hòa có là bội chung của 3, 5 và 7.

– Theo đề bài ta có xe BC(3, 5, 7) và 200 < x < 300

Vì 3, 5, 7 từng đôi một là số nguyên tố cùng nhau.

=> BCNN(3, 5, 7) = 105

=> BC(3, 5, 7) = B(105) = {0; 105, 210, 315;…}

=> x BC(3, 5, 7) = {0, 105, 210, 315,…. }.

Mà 200 ≤ x ≤ 300 nên x = 210.

Vậy số bông sen chị Hòa có là 210 bông.

Đáp án cần chọn là: A

Câu 6. Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng

BCNN(a,b) = 300.

A. 1

B. 2

C. 3

D. 300

Trả lời:

BCNN(a,b) = 300

BC(a,b) là bội của 300.

=> Tất cả các số có 3 chữ số là bội chung của a và b là: 300, 600, 900

Vậy có tất cả 3 số có ba chữ số là bội của a và b.

Đáp án cần chọn là: C

Câu 7. Tìm bội chung nhỏ nhất của: 7 và 13

A. 182

B. 91

C. 13

D. 1

Trả lời:

Vì 7 và 13 đều là hai số nguyên tố nên ƯCLN(7,13)=1

Hay 7 và 13 là hai số nguyên tố cùng nhau.

=> BCNN(7,13) = 7 . 13 = 91.

Đáp án cần chọn là: B

Câu 8. 54 và 108 có bội chung nhỏ nhất là

A. 54

B. 1

C. 108

D. 216

Trả lời:

54 =2.3³

108 =2².3³

Các thừa số chung của 54 và 108 là 2 và 3.

Số mũ lớn nhất của 2 là 2

Số mũ lớn nhất của 3 là 3.

BCNN(54,108)=2².3³=108

Đáp án cần chọn là: C

Câu 9. Thực hiện các phép tính sau: $\frac{3}{8}+\frac{5}{24}$. Với kết quả là phân số tối giản

A.$\frac{14}{28}$

B.$\frac{7}{12}$

C.$\frac{112}{192}$

D.$\frac{12}{7}$

Trả lời:

Ta có BCNN (8; 24) = 24 nên:

$\frac{3}{8}+\frac{5}{24}=\frac{3.3}{8.3}+\frac{5}{24}=\frac{9}{24}+\frac{5}{24}=\frac{14}{24}=\frac{7}{12}$

Đáp án cần chọn là: B

Câu 10. Cho tập hợp X là ước của 35 và lớn hơn 5. Cho tập Y là bội của 8 và nhỏ hơn 50. Gọi M là giao của 2tập hợp X và Y, tập hợp M có bao nhiêu phần tử?

A. 2

B. 1

C. 0

D. 3

Trả lời:

Ư(35) ={1,5,7,35}; Ư(35) > 5 ⇒ X ={7,35}

B(8) = {0,8,16,24,32,40,48,56,…}

B(8) < 50 ⇒Y={0,8,16,24,32,40,48}

Vì: X ={7,35}; Y ={0,8,16,24,32,40,48}

⇒M = X∩Y=θ⇒M = X∩Y = θnên tập M không có phần tử nào.

Đáp án cần chọn là: C

Câu 11. Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?

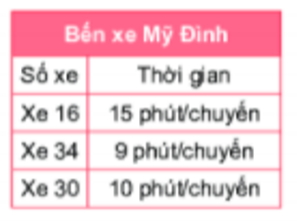
A. 90 phút

B. 45 phút

C. 180 phút

D. 30 phút

Trả lời:

Thời gian các xe cùng xuất bến cách 10h35p các khoảng thời gian là BC(9, 10, 15)

Ta có: 9 = 3², 10 = 2.5,15 = 3.5.

Thừa số chung và riêng là 2, 3 và 5

Số mũ lớn nhất của 2 là 1

Số mũ lớn nhất của 3 là 2

Số mũ lớn nhất của 5 là 1

=> BCNN(9, 10, 15) = 2.3².5 = 90

Vậy cứ 90 phút thì các xe xuất bến cùng một lúc.

Đáp án cần chọn là: A

Câu 12. Tìm số tự nhiên n lớn nhất có 3 chữ số sao cho nchia 8dư 7, chia 31dư 28.

A. 927

B. 183

C. 431

D. 729

Trả lời:

Vì n chia 8 dư 7 nên (n−7)⁝8(n > 7)

⇒n = 8a + 7 với aN

⇒(n+1)⁝8

Vì n chia 31dư 28 nên (n−28)⁝31(n > 28)

⇒ n = 31b + 28 (bN)
⇒ (n+3)⁝31

Vì 64⁝8 nên (n+1+64)⁝8 hay (n+65)⁝8(1)
Vì 62⁝31 ⇒(n+3+62)⁝31

Hay (n+65)⁝31(2)
Từ (1) và (2)

⇒(n+65)⁝BCNN(8;31)
⇒(n+65)⁝248

⇒n = 248k − 65 (kN*)
Với k = 1 ⇒n = 248.1 – 65 = 183
Với k = 2 ⇒ n = 248.2 – 65 = 431

Với k = 3 ⇒ n = 248.3 – 65 = 679

Với k = 4 ⇒ n = 248.4 – 65 = 927

Với k = 5 ⇒ n = 248.5 – 65 = 1175 (loại)
Vì nlà số lớn nhất có 3chữ số nên n = 927.

Đáp án cần chọn là: A

Câu 13. Cho a; b có BCNN(a; b) = 630; ƯCLN(a; b) = 18. Có bao nhiêu cặp số

a; b thỏa mãn?

A. 6

B. 5

C. 2

D. 3

Trả lời:

Vì ƯCLN(a;b) = 18 nên đặt a = 18x; b = 18y

với x; yN; ƯCLN(x; y) = 1; y ≠ 1.

VìƯCLN(a; b).BCNN(a; b) = a.b

Nên 18.630 = 18x.18y

⇒x.y = (18.630):(18.18) hay x.y = 35

mà y ≠ 1. Do đó ta có:

+) Nếu x = 1 thì y = 35 khi đó a = 18.1 = 18; b = 35.18 = 630

+) Nếu x = 5 thì y = 7 khi đó a = 18.5 = 90; b = 7.18 = 126

+) Nếu x = 7 thì y = 5 khi đó a = 18.7 = 126; b = 5.18 = 90

Vậy có ba cặp số a; b thỏa mãn.

Đáp án cần chọn là: D

Câu 14. Tìm hai số tự nhiên a, b(a < b). Biết a + b = 20, BCNN(a, b) = 15.

A. a = 15; b = 25.

B. a = 15; b = 5.

C. a = 15; b = 20.

D. a = 5; b = 15.

Trả lời:

Gọi ƯCLN(a,b) = d ⇒ a = d.m, b = d.n;(m,n) = 1

⇒a+b = d(m+n) ⇒d Ư(a+b) hay dƯ(20)
Vì BCNN(a,b) =15 ⇒15⁝d hay dƯ(15)
⇒d ƯC(15;20)
Mà ƯCLN(15;20) = 5 nên d = 1 hoặc d = 5
+) Nếu d = 1⇒a.b = 1.15 = 15 = 3.5
Khi đó a + b = 3 + 5 = 8 (loại)
Hoặc a + b = 1+15 = 16 (loại)
+) Nếu d = 5 thì a.b = 5.15 = 75 = 1.75
Khi đó a + b = 15 + 5 = 20 (thỏa mãn)
Hoặc a + b = 1 + 75 = 76 (loại)
Vậy hai số cần tìm là a = 5; b = 15.

Đáp án cần chọn là: D

Câu 15. Một số tự nhiên aa khi chia cho 7 dư 4; chia cho 9 dư 6. Tìm số dư khi chia a cho 63.

A. 0

B. 36

C. 3

D. 60

Trả lời:

Vì a chia cho 7 dư 4⇒(a + 3)⁝7

a chia cho 9 dư 6 ⇒(a + 3)⁝9

Do đó (a + 3)BC(7; 9) mà BCNN(7; 9) = 63.

Do đó a(a+3)⁝63⇒a chia cho 63 dư.60.

Đáp án cần chọn là: D

Phần 2. Lý thuyết Bội chung, Bội chung nhỏ nhất

1. Bội chung

Một số được gọi là bội chung của hai hay nhiều số nếu nó là bội của tất cả các số đó.

Ví dụ: Ta có: B(9) = {0; 9; 18; 27; 36; 45; 54; 63; 72; …};

B(12) = {0; 12; 24; 36; 48; 60; 72; …}.

Hai tập hợp này có một số phần tử chung như 0; 36; 72; … Ta nói chúng là các bội chung của 9 và 12.

• Kí hiệu tập hợp các bội chung của a và b là BC(a, b).

• Tương tự, tập hợp các bội chung của a, b, c là BC(a, b, c).

Ví dụ:

– Tập hợp các bội chung của 15 và 55 là BC(15, 55).

– Tập hợp các bội chung của 16; 20; 25 là BC(16, 20, 25).

Cách tìm bội chung của hai số a và b:

– Viết tập hợp B(a) và bội B(b).

– Tìm những phần tử chung của B(a) và B(b).

Ví dụ:

Ta có: B(2) = {0; 2; 4; 6; 8; 10; 12; …}

B(3) = {0; 3; 6; 9; 12; …}

Những phần tử chung của B(2) và B(3) là 0; 6; 12; …

Do đó BC(2, 3) = {0; 6; 12; …}.

2. Bội chung nhỏ nhất

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu bội chung nhỏ nhất của a và b là BCNN(a, b).

Tương tự, bội chung nhỏ nhất của a, b và c là BCNN(a, b, c).

Nhận xét: Tất cả các bội chung của a và b đều là bội của BCN(a, b). Mọi số tự nhiên đều là bội của 1.

Do đó, với mọi số tự nhiên a và b (khác 0) ta có:

BCNN(a, 1) = a;

BCNN(a, b, 1) = BCNN(a, b).

Ví dụ:

• Ta có: BC(6, 8) = {0; 24; 48; 72; …} vì 24 là số nhỏ nhất khác 0 trong số các bội chung của 6 và 8, nên BCNN(6, 8) = 24.

Tất cả các bội chung của 6 và 8 (là 0; 24; 48; 72; …) đều là bội của BCNN(6, 8) là 24.

• BCNN(8, 1) = 1;

• BCNN(6, 8, 1) = BCNN(6, 8) = 24.

3. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

Quy tắc:

Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau:

Bước 1: Phân tích mỗi số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung và riêng.

Bước 3: Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.

Ví dụ: Tìm BCNN của 15 và 20.

Hướng dẫn giải

Ta có: 15 = 3 . 5; 20 = 2² . 5.

Thừa số nguyên tố chung và riêng là 2; 3 và 5.

Số mũ lớn nhất của 2 là 2; của 3 là 1 và của 5 là 1.

Do đó BCNN(15, 20) = 2² . 3 . 5 = 60.

Chú ý:

• Nếu các số đã cho từng đôi một nguyên tố cùng nhau thì BCNN của chúng là tích của các số đó.

Ví dụ: 3 và 8; 8 và 11; 11 và 3 là các cặp đôi một nguyên tố cùng nhau.

Khi đó, BCNN(3, 8, 11) = 3 . 8 . 11 = 264.

• Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.

Ví dụ: Ta có BCNN(6, 12, 36) = 36 vì 36 ⋮ 9; 36 ⋮ 12 và 36 lớn hơn 9 và 12.

4. Ứng dụng trong quy đồng mẫu các phân số

Quy tắc:

Muốn quy đồng mẫu số nhiều phân số ta có thể làm như sau:

Bước 1: Tìm một bội chung của các mẫu số (thường là BCNN) để làm mẫu số chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu số (bằng cách chia mẫu số chung cho từng mẫu số riêng).

Bước 3: Nhân tử số và mẫu số của mỗi phân số với thừa số phụ tương ứng.

Ví dụ: Quy đồng mẫu số hai phân số 7/30 và 5/42.

Hướng dẫn giải

Ta có: 30 = 2 . 3 . 5; 42 = 2 . 3 . 7.

Thừa số nguyên tố chung và riêng là 2; 3; 5 và 7.

Số mũ lớn nhất của 2; 3; 5 và 7 đều là 1.

Khi đó, BCNN(30, 42) = 2 . 3 . 5 . 7 = 210.

Do đó BC(30; 42) = {0; 210; 420; …}

Cách 1: Chọn mẫu chung là 210. Ta được:

 .

Cách 2: Chọn mẫu chung là một bội chung bất kì khác 0 của 30 và 42.

Chẳng hạn: chọn mẫu chung là 420, ta được:

 .

Xem thêm các bài trắc nghiệm Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 11: Ước chung, Ước chung lớn nhất

Trắc nghiệm Bài 12: Bội chung, Bội chung nhỏ nhất

Trắc nghiệm Bài 1: Số nguyên âm và tập hợp các số nguyên

Trắc nghiệm Bài 2: Thứ tự trong tập hợp số nguyên

Trắc nghiệm Bài 3: Phép cộng và phép trừ hai số nguyên