24 câu Trắc nghiệm Toán 6 Chương 5 (Chân trời sáng tạo): Phân số có đáp án 2023

Trắc nghiệm Toán lớp 6 Chương 5: Phân số 

Phần 1. Trắc nghiệm Chương 5: Phân số

Câu 1: Sắp xếp các phân số sau: $\frac{1}{3};\frac{1}{2};\frac{3}{8};\frac{6}{7}$  theo thứ tự từ lớn đến bé.

A.  $\frac{1}{2};\frac{3}{8};\frac{1}{3};\frac{6}{7}$

B.  $\frac{6}{7};\frac{1}{2};\frac{3}{8};\frac{1}{3}$

C.  $\frac{1}{2};\frac{1}{3};\frac{3}{8};\frac{6}{7}$

D.  $\frac{6}{7};\frac{3}{8};\frac{1}{3};\frac{1}{2}$

Trả lời:

Ta có:  $\frac{1}{3}=\frac{6}{18};\frac{1}{2}=\frac{6}{12};\frac{3}{8}=\frac{6}{16}.$

Vì  $\frac{6}{18}<\frac{6}{16}<\frac{6}{12}<\frac{6}{7}\Rightarrow \frac{6}{7}>\frac{1}{2}>\frac{3}{8}>\frac{1}{3}$

Vậy các phân số trên được sắp xếp theo thứ tự từ lớn đến bé là: $\frac{6}{7};\frac{1}{2};\frac{3}{8};\frac{1}{3}.$

Đáp án cần chọn là: B

Câu 2: Rút gọn phân số $\frac{-24}{105}$  đến tối giản ta được:

A.  $\frac{8}{35}$

B.  $\frac{-8}{35}$

C.  $\frac{-12}{35}$

D.  $\frac{12}{35}$

Trả lời:

 $\frac{-24}{105}=\frac{-24:3}{105:3}=\frac{-8}{35}$

Đáp án cần chọn là: B

Câu 3: Tìm một phân số ở giữa hai phân số $\frac{1}{10}$ và  $\frac{2}{10}$.

A.  $\frac{3}{10}$

B.  $\frac{15}{10}$

C.  $\frac{15}{100}$

D. Không có phân số nào thỏa mãn.

Trả lời:

Ta có:  $\frac{1}{10}=\mathrm{0,1};\frac{2}{10}=\mathrm{0,2}$

Vậy số cần tìm phải thỏa mãn: 0,1 < x < 0,2 nên trong các đáp án trên thì x chỉ có thể là  $\mathrm{0,15}=\frac{15}{100}.$

Đáp án cần chọn là: C

Câu 4: Tính $3\frac{3}{5}+1\frac{1}{6}$

A.  $4\frac{23}{30}$

B.  $5\frac{23}{30}$

C. $2\frac{23}{30}$ 

D.  $3\frac{23}{30}$

Trả lời:

 $3\frac{3}{5}+1\frac{1}{6}=\left(3+1\right)+\left(\frac{3}{5}+\frac{1}{6}\right)=4+\frac{23}{30}=4\frac{23}{30}.$

Đáp án cần chọn là: A

Câu 5: Tính $\frac{6}{15}+\frac{12}{-15}$ là:

A.  $\frac{18}{15}$

B.  $\frac{-2}{5}$

C.  $\frac{1}{5}$

D.  $\frac{-1}{5}$

Trả lời:

 $\frac{6}{15}+\frac{12}{-15}=\frac{6}{15}+\left(\frac{-12}{15}\right)=\frac{6+\left(-12\right)}{15}=\frac{-6}{15}=\frac{-2}{5}$

Đáp án cần chọn là: B

Câu 6: Phân số $\frac{2}{5}$ viết dưới dạng số thập phân là:

A.2,5

B.5,2

C.0,4

D.0,04

Trả lời:

$\frac{2}{5}=\frac{4}{10}=\mathrm{0,4.}$

Đáp án cần chọn là: C

Câu 7: Hỗn số $1\frac{2}{5}$  được chuyển thành số thập phân là:

A.1,2

B.1,4

C.1,5

D.1,8

Trả lời:

 $1\frac{2}{5}=\frac{1.5+2}{5}=\frac{7}{5}=\frac{14}{10}=\mathrm{1,4.}$

Đáp án cần chọn là: B

Câu 8: Số thập phân 3,015 được chuyển thành phân số là:

A.  $\frac{3015}{10}$

B.  $\frac{3015}{100}$

C.  $\frac{3015}{1000}$

D.  $\frac{3015}{10000}$

Trả lời:

 $\mathrm{3,015}=\frac{3015}{1000}$

Đáp án cần chọn là: C

Câu 9: Phân số nghịch đảo của phân số:  $\frac{-4}{5}$ là:

A.  $\frac{4}{5}$

B.  $\frac{4}{-5}$

C.  $\frac{5}{4}$

D.$\frac{-5}{4}$

Trả lời:

Phân số nghịch đảo của phân số: $\frac{-4}{5}$ là $\frac{-5}{4}$ .

Đáp án cần chọn là: D

Câu 10: Số tự nhiên x thỏa mãn: 35,67 < x < 36,05 là:

A.35

B.36

C.37

D.34

Trả lời:

Ta có: 35,67 < x < 36,05 và x là số tự nhiên nên x = 36.

Đáp án cần chọn là: B

Câu 11: Cho hai biểu thức $B=\left(\frac{2}{3}-1\frac{1}{2}\right):\frac{4}{3}+\frac{1}{2}$  và $C=\frac{9}{23}.\frac{5}{8}+\frac{9}{23}.\frac{3}{8}-\frac{9}{23}$ . Chọn câu đúng

A. B < 0, C = 0

B. B > 0, C = 0

C. B < 0, C < 0

D. B = 0, C < 0

Trả lời:

 $B=\left(\frac{2}{3}-1\frac{1}{2}\right):\frac{4}{3}+\frac{1}{2}=\left(\frac{2}{3}-\frac{3}{2}\right).\frac{3}{4}+\frac{1}{2}=\frac{-5}{6}.\frac{3}{4}+\frac{1}{2}=\frac{-5}{8}+\frac{1}{2}=\frac{-1}{8}.$

 $\begin{array}{l}C=\frac{9}{23}.\frac{5}{8}+\frac{9}{23}.\frac{3}{8}-\frac{9}{23}\\ =\frac{9}{23}.\left(\frac{5}{8}+\frac{3}{8}-1\right)\\ =\frac{9}{23}.\left(1-1\right)\\ =\frac{9}{23}.0\\ =0.\end{array}$

Vậy C = 0; B < 0

Đáp án cần chọn là: A

Câu 12: Rút gọn phân số $\frac{1978.1979+1980.21+1958}{1980.1979-1978.1979}$ ta được kết quả là:

A. 2000

B. 1000

C. 100

D. 200

Trả lời:

$\frac{1978.1979+1980.21+1958}{1980.1979-1978.1979}=\frac{1978.1979+\left(1979+1\right).21+1958}{1979\left(1980-1978\right)}=\frac{1978.1979+1979.21+21+1958}{1979.2}=\frac{1978.1979+1979.21+1979}{1979.2}=\frac{1979.\left(1978+21+1\right)}{1979.2}=\frac{2000}{2}=1000$

Đáp án cần chọn là: B

Câu 13: Cho x là giá trị thỏa mãn  $\frac{6}{7}x-\frac{1}{2}=1$

A.  $x=\frac{9}{14}$

B.  $x=\frac{7}{4}$

C.  $x=\frac{-7}{4}$

D.  $x=\frac{9}{7}$

Trả lời:

 $\begin{array}{l}\frac{6}{7}x-\frac{1}{2}=1\\ \frac{6}{7}x=1+\frac{1}{2}\\ \frac{6}{7}x=\frac{3}{2}\\ x=\frac{3}{2}:\frac{6}{7}\\ x=\frac{7}{4}.\end{array}$

Đáp án cần chọn là: B

Câu 14: Cho  x₁ là giá trị thỏa mãn  và  $\frac{1}{2}-(\frac{2}{3}x-\frac{1}{3})=\frac{-2}{3}$ là giá trị thỏa mãn $\frac{5}{6}-x=\frac{-1}{12}+\frac{4}{3}$ . Khi đó   bằng

A.  $\frac{8}{3}$

B.  $\frac{-5}{12}$

C.  $\frac{9}{4}$

D.  $\frac{11}{6}$

Trả lời:

 $\begin{array}{l}+)\frac{1}{2}-\left(\frac{2}{3}x-\frac{1}{3}\right)=\frac{-2}{3}\\ \frac{2}{3}x-\frac{1}{3}=\frac{1}{2}-\left(\frac{-2}{3}\right)\\ \frac{2}{3}x-\frac{1}{3}=\frac{7}{6}\\ \frac{2}{3}x=\frac{7}{6}+\frac{1}{3}\\ \frac{2}{3}x=\frac{3}{2}\\ x=\frac{3}{2}:\frac{2}{3}\\ x=\frac{9}{4}.\end{array}$

Nên  $x_1=\frac{9}{4}$

 $\begin{array}{l}+)\frac{5}{6}-x=\frac{-1}{12}+\frac{4}{3}\\ \frac{5}{6}-x=\frac{5}{4}\\ x=\frac{5}{6}-\frac{5}{4}\\ x=\frac{-5}{12}.\end{array}$

Nên  $x_2=-\frac{5}{12}$

Từ đó  $x_1+x_2=\frac{9}{4}+\left(-\frac{5}{12}\right)=\frac{11}{6}$

Đáp án cần chọn là: D

Câu 15: Rút gọn phân số  $A=\frac{7.9+14.27+21.36}{21.27+42.81+63.108}$ đến tối giản ta được kết quả là phân số có mẫu số là

A.9

B.1

C. 

D.2

Trả lời:

Ta có:

$\begin{array}{l}A=\frac{7.9+14.27+21.36}{21.27+42.81+63.108}\\ =\frac{7.9\left(1+2.3+3.4\right)}{21.27\left(1+2.3+3.4\right)}\\ =\frac{7.9}{\mathrm{3.7.9.3}}\\ =\frac{1}{9}\end{array}$

Đáp án cần chọn là: A

Câu 16: Cho $A=\frac{\left(3\frac{2}{15}+\frac{1}{5}\right):2\frac{1}{2}}{\left(5\frac{3}{7}-2\frac{1}{4}\right):4\frac{43}{56}}$ và $B=\frac{\mathrm{1,2}:\left(1\frac{1}{5}.1\frac{1}{4}\right)}{\mathrm{0,32}+\frac{2}{25}}$  . Chọn đáp án đúng.

A. A < -B

B. 2A > B

C. A > B

D. A = B

Trả lời:

Ta có  $A=\frac{\left(3\frac{2}{15}+\frac{1}{5}\right):2\frac{1}{2}}{\left(5\frac{3}{7}-2\frac{1}{4}\right):4\frac{43}{56}}=\frac{\left(\frac{47}{15}+\frac{3}{15}\right):\frac{5}{2}}{\left(\frac{38}{7}-\frac{9}{4}\right):\frac{267}{56}}=\frac{\frac{50}{15}.\frac{2}{5}}{\left(\frac{152}{28}-\frac{63}{28}\right).\frac{56}{267}}=\frac{\frac{4}{3}}{\frac{89}{28}.\frac{56}{267}}=\frac{\frac{4}{3}}{\frac{2}{3}}=2$

Và  $B=\frac{\mathrm{1,2}:\left(1\frac{1}{5}.1\frac{1}{4}\right)}{\mathrm{0,32}+\frac{2}{25}}=\frac{\frac{6}{5}:\left(\frac{6}{5}.\frac{5}{4}\right)}{\frac{8}{25}+\frac{2}{25}}=\frac{\frac{6}{5}:\frac{3}{2}}{\frac{10}{25}}=\frac{\frac{4}{5}}{\frac{2}{5}}=2$

Vậy A = B.

Đáp án cần chọn là: D

Câu 17: Người ta mở vòi cho nước chảy vào đầy bể cần 3 giờ. Hỏi nếu mở vòi nước đó trong 45 phút thì được bao nhiêu phần của bể?

A.  $\frac{1}{3}$

B.  $\frac{1}{4}$

C.  $\frac{2}{3}$

D.  $\frac{1}{2}$

Trả lời:

Đổi: 45phút = $\frac{3}{4}$ giờ

Mỗi giờ vòi nước chảy được số phần bể là: $1:3=\frac{1}{3}$ (bể)

Nếu mở vòi trong 45 phút thì được số phần bể là: $\frac{3}{4}.\frac{1}{3}=\frac{1}{4}$ (bể)

Đáp án cần chọn là: B

Câu 18: Lúc 7 giờ 5 phút, một người đi xe máy đi từ A và đến B lúc 8 giờ 45 phút. Biết quãng đường AB dài 65km. Tính vận tốc của người đi xe máy đó?

A.39 km/h

B.40 km/h

C.42 km/h

D.44 km/h

Trả lời:

Thời gian người đó đi hết quãng đường AB là: 8 giờ 45 phút – 7 giờ 5 phút = 1 giờ 40 phút

Đổi 1 giờ 40 phút = $\frac{5}{3}$ giờ.

Vận tốc của người đi xe máy đó là: $65:\frac{5}{3}=39\left(km/h\right)$    

Đáp án cần chọn là: A

Câu 19: Chọn câu đúng

A.  $\frac{23}{99}<\frac{2323}{9999}<\frac{232323}{999999}<\frac{23232323}{99999999}$

B.  $\frac{23}{99}>\frac{2323}{9999}>\frac{232323}{999999}>\frac{23232323}{99999999}$

C.  $\frac{23}{99}=\frac{2323}{9999}<\frac{232323}{999999}=\frac{23232323}{99999999}$

D.  $\frac{23}{99}=\frac{2323}{9999}=\frac{232323}{999999}=\frac{23232323}{99999999}$

Trả lời:

Ta có:

$\frac{2323}{9999}=\frac{2323:101}{9999:101}=\frac{23}{99}\frac{232323}{999999}=\frac{232323:10101}{999999:10101}=\frac{23}{99}\frac{23232323}{99999999}=\frac{23232323:1010101}{99999999:1010101}=\frac{23}{99}$

Vậy  $\frac{23}{99}=\frac{2323}{9999}=\frac{232323}{999999}=\frac{23232323}{99999999}$

Đáp án cần chọn là: D

Câu 20: Không qui đồng, hãy so sánh hai phân số sau:  $\frac{37}{67}$ và $\frac{377}{677}$ .

A.  $\frac{37}{67}<\frac{377}{677}$

B.  $\frac{37}{67}>\frac{377}{677}$

C.  $\frac{37}{67}=\frac{377}{677}$

D. $\frac{37}{67}\ge \frac{377}{677}$ 

Trả lời:

Ta có :

$1-\frac{37}{67}=\frac{30}{67};1-\frac{377}{677}=\frac{300}{677}.$

Lại có: $\frac{30}{67}=\frac{300}{670}>\frac{300}{677}$ nên $\frac{37}{67}<\frac{377}{677}$.  

Đáp án cần chọn là: A

Câu 21:Tính nhanh  $A=\frac{5}{1.3}+\frac{5}{3.5}+\frac{5}{5.7}+\mathrm{\dots }+\frac{5}{99.101}$

A.  $\frac{205}{110}$

B.  $\frac{250}{110}$

C.  $\frac{205}{101}$

D.  $\frac{250}{101}$

Trả lời:

 $\begin{array}{l}A=\frac{5}{1.3}+\frac{5}{3.5}+\frac{5}{5.7}+\mathrm{\dots }+\frac{5}{99.101}\\ =5.\left(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+\mathrm{\dots }+\frac{1}{99.101}\right)\\ =\frac{5}{2}.\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\mathrm{\dots }+\frac{1}{99}-\frac{1}{101}\right)\\ \begin{array}{l}=\frac{5}{2}.\left(1-\frac{1}{101}\right)\\ =\frac{5}{2}.\frac{100}{101}=\frac{250}{101}.\end{array}\end{array}$

Đáp án cần chọn là: D

Câu 22:Chọn câu đúng

A.  $\frac{31}{2}.\frac{32}{2}.\frac{33}{2}\mathrm{\dots .}\frac{60}{2}=\mathrm{1.2.3.4.5.6.7\dots 60}$

B.  $\frac{31}{2}.\frac{32}{2}.\frac{33}{2}\mathrm{\dots .}\frac{60}{2}=\mathrm{1.3.5.7\dots 59}$

C.  $\frac{31}{2}.\frac{32}{2}.\frac{33}{2}\mathrm{\dots .}\frac{60}{2}=\mathrm{1.3.5.7\dots 60}$

D.  $\frac{31}{2}.\frac{32}{2}.\frac{33}{2}\mathrm{\dots .}\frac{60}{2}=\mathrm{2.4.6.8\dots 60}$

Trả lời:

Ta có  $\frac{31}{2}.\frac{32}{2}.\frac{33}{2}\mathrm{\dots .}\frac{60}{2}=\frac{\mathrm{31.32.33\dots 60}}{\mathrm{2.2.2\dots .2}}=\frac{\left(\mathrm{31.32.33\dots 60}\right)\left(\mathrm{1.2.3\dots 30}\right)}{2^{30}\left(\mathrm{1.2.3\dots 30}\right)}$

$=\frac{\mathrm{1.2.3.4.5\dots 60}}{\left(1.2\right).\left(2.2\right).\left(3.2\right).\left(4.2\right)\mathrm{\dots }\left(30.2\right)}=\frac{\left(\mathrm{2.4.6\dots 60}\right)\left(\mathrm{1.3.5.7\dots 59}\right)}{\mathrm{2.4.6\dots 60}}=\mathrm{1.3.5\dots 59}$

Đáp án cần chọn là: B

Câu 23:Cho phân số $A=\frac{n-5}{n+1}\left(n\in Z;n\ne -1\right)$ dụng

Có bao nhiêu giá trị nguyên của nn để A có giá trị nguyên.

A.10

B.8

C.6

D.4

Trả lời:

Ta có  $A=\frac{n-5}{n+1}=\frac{n+1-6}{n+1}=\frac{n+1}{n+1}-\frac{6}{n+1}=1-\frac{6}{n+1}$

Để A có giá trị nguyên thì 6⋮ (n + 1) ⇒ (n + 1) ∈ Ư(6) = {±1; ±2; ±3; ±6}

Ta có bảng sau

n+1	1	-1	2	-2	3	-3	6	-6
n	0	-2	1	-3	2	-4	5	-7

Vậy có 8 giá trị của n thỏa mãn là 0; −2; 1; −3; 2; −4; 5; −7.

Đáp án cần chọn là: B

Câu 24: Cho phân số $A=\frac{n-5}{n+1}\left(n\in Z;n\ne -1\right)$ dụng

Tìm điều kiện của n để A là phân số tối giản.

A. n ≠ 2k – 1 (k ∈ Z)

B. n ≠ 3k – 1 (k ∈ Z)

C. n ≠ 2k – 1 (k ∈ Z) và n ≠ 3k – 1 (k ∈ Z)

D. n ≠ 2k (k ∈ Z) và n ≠ 3k(k ∈ Z)

Trả lời:

Để A tối giản thì (n-5) và (n+1) là hai số nguyên tố cùng nhau ⇒(n − 5; n + 1) = 1

⇔ (n + 1 – n + 5; n + 1) = 1⇔ (n + 1; 6) = 1

Từ đó (n + 1) không chia hết cho 2 và (n + 1) không chia hết cho 3 

Hay n ≠ 2k – 1 và n ≠ 3k – 1 (k ∈ Z)

Đáp án cần chọn là: C

Phần 2. Lý thuyết Chương 5: Phân số

1. Khái niệm phân số

Ta gọi 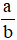, trong đó  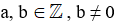là phân số, a là tử số (tử), b là mẫu số (mẫu) của phân số. Phân số  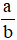đọc là a phần b.

2. Phân số bằng nhau
 Hai phân số 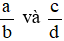 được gọi là bằng nhau, viết là 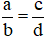, nếu a . d = b . c.

Chú ý: Điều kiện a . d = b . c gọi là điều kiện bằng nhau của hai phân số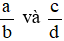  

3. Biểu diễn số nguyên ở dạng phân số 

Mỗi số nguyên n có thể coi là phân số 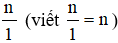. Khi đó số nguyên n được biểu diễn ở dạng phân số .

4. Tính chất cơ bản của phân số

– Tính chất 1: Nếu nhân cả tử số và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho.

– Áp dụng tính chất 1, ta có thể quy đồng mẫu số hai phân số bằng cách nhân tử và mẫu mỗi phân số với số nguyên thích hợp.

2. Tính chất 2

– Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho.

Áp dụng tính chất 2, ta có thể rút gọn phân số bằng cách chia cả tử và mẫu cho cùng ước chung khác 1 và −1.

5. So sánh hai phân số có cùng mẫu

Quy tắc 1. Với hai phân số có cùng một mẫu dương: Phân số nào có tử số nhỏ hơn thì phân số đó nhỏ hơn, phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

6. So sánh hai phân số khác mẫu

Quy tắc 2. Để so sánh hai phân số có mẫu khác nhau, ta viết hai phân số đó ở dạng hai phân số có cùng một mẫu dương rồi so sánh hai phân số mới nhận được.

7. Áp dụng quy tắc so sánh phân số

Nhờ viết số nguyên dưới dạng phân số, ta so sánh được số nguyên với phân số.

Chú ý: Khi so sánh phân số ta có thể áp dụng tính chất bắc cầu. Nghĩa là: 

Nếu có 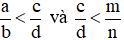 thì ta có .

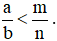Nhận xét: 

– Phân số nhỏ hơn số 0 gọi là phân số âm. Phân số lớn hơn số 0 là phân số dương.

– Theo tính chất bắc cầu, phân số âm nhỏ hơn phân số dương.

8. Phép cộng hai phân số

Quy tắc cộng hai hai phân số cùng mẫu: Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.

Quy tắc cộng hai phân số khác mẫu: Muốn cộng hai phân số khác mẫu, ta quy đồng mẫu số của chúng 

Một số tính chất của phép cộng phân số: Phép cộng phân số có các tính chất giao hoán và kết hợp, cộng một phân số với 0 ta được chính nó.

9. Số đối

Hai phân số là đối nhau nếu tổng của chúng bằng 0.

Kí hiệu số đối của phân số .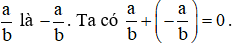

Mà 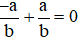 nên ta có: .

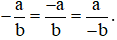10. Phép trừ hai phân số

Muốn trừ một phân số cho một phân số, ta lấy phân số thứ nhất cộng với số đối của phân số thứ hai.

Quy tắc dấu ngoặc:

– Khi bỏ ngoặc có dấu cộng (+) đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

– Khi bỏ ngoặc có dấu trừ (−) đằng trước, ta phải đổi dấu tất cả các số hạng trong ngoặc.

Chú ý: Ta thực hiện được phép cộng và phép trừ phân số với số nguyên bằng cách viết số nguyên ở dạng phân số.

11. Nhân hai phân số

 Quy tắc: Muốn nhân hai phân số, ta nhân tử số với nhau và nhân hai mẫu số với nhau.

– Một số tính chất của phép nhân phân số: Phép nhân phân số có các tính chất: giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng.

Chú ý: Khi nhân một phân số với 1 ta được chính nó.

12. Chia phân số

Quy tắc chia phân số: Muốn chia một phân số cho một phân số khác 0 ta nhân phân số thứ nhất với phân số có tử số là mẫu số của phân số thứ hai và mẫu số là tử số của phân số thứ nhất.

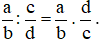
Chú ý: Ta thực hiện được phép nhân và phép chia phân số với số nguyên bằng cách viết số nguyên dưới dạng phân số.

13. Tính giá trị phân số của một số

Quy tắc 1: Muốn tính giá trị phân số 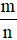 của số a, ta tính .

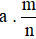14. Tìm một số khi biết giá trị phân số của số đó

Quy tắc 2: Muốn tìm một số khi biết giá trị phân số 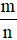 của nó là b, ta tính .

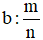15. Hỗn số

Cho a và b là hai số nguyên dương, a > b, a không chia hết cho b. Nếu a chia cho b được thương là q và số dư là r, thì ta viết 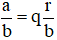 và gọi  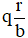là hỗn số.

Chú ý: Với hỗn số 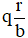 người ta gọi q là phần số nguyên và  là phần phân số của hỗn số.

16. Đổi hỗn số ra phân số

Ta biết viết phân số 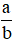 với a > b > 0 thành hỗn số .

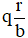Ngược lại, ta đổi được hỗn số 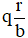 thành phân số, theo quy tắc sau:

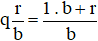
Xem thêm các bài trắc nghiệm Toán lớp 6 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Chương 4: Một số yếu tố thống kê

Trắc nghiệm Chương 5: Phân số

Trắc nghiệm Chương 6: Số thập phân

Trắc nghiệm Chương 7: Hình học trực quan

Trắc nghiệm Chương 8: Hình học phẳng và các hình học cơ bản