Sách bài tập Toán 10 Bài 3 (Chân trời sáng tạo): Phương trình quy về phương trình bậc hai

Giải SBT Toán lớp 10 Bài 3: Phương trình quy về phương trình bậc hai

Giải SBT Toán 10 trang 18 Tập 2

Bài 1 trang 18 SBT Toán 10 Tập 2: Giải các phương trình sau:

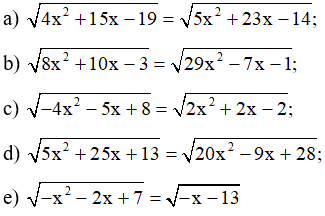
Ý b

Ý c

Ý d

Ý e

Lời giải:

a) $\sqrt{4x^2+15x-19}=\sqrt{5x^2+23x-14}$

Bình phương hai vế của phương trình đã cho, ta được:

4x² + 15x – 19 = 5x² + 23x – 14

⇒ x² + 8x + 5 = 0

⇒ x = –4 + $\sqrt{11}$ hoặc x = –4 – $\sqrt{11}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có –4 – $\sqrt{11}$ thỏa mãn.

Vậy nghiệm của phương trình đã cho là –4 – $\sqrt{11}$.

b) $\sqrt{8x^2+10x-3}=\sqrt{29x^2-7x-1}$

Bình phương hai vế của phương trình đã cho, ta được:

8x² + 10x – 3 = 29x² – 7x – 1

⇒ 21x² – 17x + 2 = 0

⇒ x = $\frac{2}{3}$ hoặc x = $\frac{1}{7}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có $\frac{2}{3}$ thỏa mãn. Vậy nghiệm của phương trình đã cho là  $\frac{2}{3}$.

c) $\sqrt{-4x^2-5x+8}=\sqrt{2x^2+2x-2}$

Bình phương hai vế của phương trình đã cho, ta được:

–4x² – 5x + 8  = 2x² + 2x – 2

⇒ 6x² + 7x – 10 = 0

⇒ x = $\frac{5}{6}$ hoặc x = –2

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{5}{6}$ và x = –2 đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là  x = $\frac{5}{6}$ và x = –2.

d) $\sqrt{5x^2+25x+13}=\sqrt{20x^2-9x+28}$

Bình phương hai vế của phương trình đã cho, ta được:

5x² + 25x + 13 = 20x² – 9x + 28

⇒ 15x² – 34x + 15 = 0

⇒ x = $\frac{5}{3}$ hoặc x = $\frac{3}{5}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{5}{3}$ hoặc x = $\frac{3}{5}$ đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là  x = $\frac{5}{3}$ và x = $\frac{3}{5}$.

e) $\sqrt{-x^2-2x+7}=\sqrt{-x-13}$

⇒ –x² – 2x + 7 =  – x – 13

⇒ x² + x – 20 = 0

⇒ x = 4 hoặc x = –5

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 4 hoặc x = –5 đều không thỏa mãn.

Vậy phương trình vô nghiệm.

Bài 2 trang 18 SBT Toán 10 Tập 2: Giải các phương trình sau:

a) $2\sqrt{x^2+4x-7}=\sqrt{-4x^2+38x-43};$

b) $\sqrt{6x^2+7x-1}-\sqrt{-29x^2-41x+10}=0.$

Lời giải:

a) $2\sqrt{x^2+4x-7}=\sqrt{-4x^2+38x-43};$

Bình phương hai vế của phương trình đã cho, ta được:

4.( x² + 4x – 7 ) = –4x² + 38x – 43

⇒ 8x² – 22x + 15 = 0

⇒ x = $\frac{5}{4}$ hoặc x = $\frac{3}{2}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{3}{2}$ thỏa mãn. Vậy nghiệm của phương trình đã cho là  x = $\frac{3}{2}$.

b) $\sqrt{6x^2+7x-1}-\sqrt{-29x^2-41x+10}=0.$

⇔ $\sqrt{6x^2+7x-1}=\sqrt{-29x^2-41x+10}$

Bình phương hai vế của phương trình đã cho, ta được:

6x² + 7x – 1 = –29x² – 41x + 10

⇒ 35x² + 48x – 11 = 0

⇒ x = $\frac{1}{5}$ hoặc x = $\frac{–11}{7}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{3}{5}$ hoặc x = $\frac{–11}{7}$ đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là  x = $\frac{3}{5}$ và x = $\frac{–11}{7}$.

Bài 3 trang 18 SBT Toán 10 Tập 2: Giải các phương trình sau:

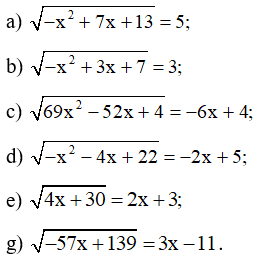
Ý b

Ý c

Ý d

Ý e

Ý g

Lời giải:

a) $\sqrt{-x^2+7x+13}=5$

Bình phương hai vế của phương trình đã cho, ta được:

–x² + 7x + 13 = 25

⇒ –x² + 7x – 12 = 0

⇒ x = 4 hoặc x = 3.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 4 hoặc x = 3 đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 4 và x = 3.

b) $\sqrt{-x^2+3x+7}=3;$

Bình phương hai vế của phương trình đã cho, ta được:

–x² + 3x + 7 = 9

⇒ –x² + 3x – 2 = 0

⇒ x = 2 hoặc x = 1.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 2 hoặc x = 1 đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 2 và x = 1.

c) $\sqrt{69x^2-52x+4}=-6x+4;$

Bình phương hai vế của phương trình đã cho, ta được:

69x² – 52x + 4 = 36x² – 48x + 16

⇒ 33x² – 4x – 12 = 0

⇒ x = $\frac{2}{3}$ hoặc x = $\frac{–6}{11}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{2}{3}$ hoặc x = $\frac{–6}{11}$ đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = $\frac{2}{3}$ và x = $\frac{–6}{11}$.

d) $\sqrt{-x^2-4x+22}=-2x+5$

Bình phương hai vế của phương trình đã cho, ta được:

–x² – 4x + 22 = 4x² – 20x + 25

⇒ 5x² – 16x + 3 = 0

⇒ x = 3 hoặc x = $\frac{1}{5}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{1}{5}$ thỏa mãn. Vậy nghiệm của phương trình đã cho là x = $\frac{1}{5}$.

e) $\sqrt{4x+30}=2x+3$

Bình phương hai vế của phương trình đã cho, ta được:

4x + 30 = 4x² + 12x + 9

⇒ 4x² + 8x – 21 = 0

⇒ x = $\frac{3}{2}$ hoặc x = $\frac{–7}{2}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{3}{2}$ thỏa mãn. Vậy nghiệm của phương trình đã cho là x = $\frac{3}{2}$.

g) $\sqrt{-57x+139}=3x-11$

Bình phương hai vế của phương trình đã cho, ta được:

–57x + 139 = 9x² – 66x + 121

⇒ 9x² – 9x – 18 = 0

⇒ x = 2 hoặc x = –1.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

Bài 4 trang 18 SBT Toán 10 Tập 2: Giải các phương trình sau:

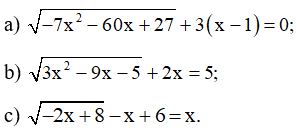
Ý b

Ý c

Lời giải:

a) $\sqrt{-7x^2-60x+27}=-3\left(x-1\right)$

Bình phương hai vế của phương trình đã cho, ta được:

–7x² – 60x + 27 = 9 (x² – 2x + 1)

⇒ 16x² + 42x – 18 = 0

⇒ x = $\frac{3}{8}$ hoặc x = –3.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{3}{8}$ hoặc x = –3 đều thỏa mãn.

Vậy phương trình đã cho có nghiệm x = $\frac{3}{8}$ và x = –3.

b) $\sqrt{3x^2-9x-5}+2x=5$

⇔ $\sqrt{3x^2-9x-5}=5-2x$

Bình phương hai vế của phương trình đã cho, ta được:

3x² – 9x – 5 = 25 – 20x + 4x²

⇒ x² – 11x + 30 = 0

⇒ x = 6 hoặc x = 5.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 6 hoặc x = 5 đều không thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

c) $\sqrt{-2x+8}-x+6=x.$

Suy ra $\sqrt{-2x+8}=2x-6.$

Bình phương hai vế của phương trình đã cho, ta được:

– 2x + 8 = 36 – 24x + 4x²

⇒ 4x² – 22x + 28 = 0

⇒ x = 2 hoặc x = .

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{7}{2}$ thỏa mãn. Vậy nghiệm của phương trình đã cho là x = $\frac{7}{2}$.

Giải SBT Toán 10 trang 19 Tập 2

Bài 5 trang 19 SBT Toán 10 Tập 2: Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc 60° đến vị trí A sau đó đi tiếp 3m đến vị trí B như Hình 1.

a) Biểu diễn khoảng cách AC và BC theo x.

b) Tìm x để $AC=\frac{8}{9}BC$

c) Tìm x để khoảng cách BC = 2AN.

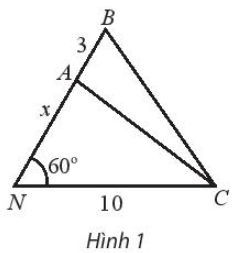
Lưu ý: Đáp số làm tròn đến hàng phần mười.

Lời giải:

a) Vì x là khoảng cách AN nên x > 0

Áp dụng định lí côsin cho tam giác ANC:

AC² = AN² + NC² – 2.AN.NC.cos60°

AC² = x² + 100 – 2.x.10.$\frac{1}{2}$ = x² – 10x + 100

Như vậy AC = $\sqrt{x^2–10x+100}$

Áp dụng định lí côsin cho tam giác BNC:

BC² = BN² + NC² – 2.AN.NC.cos60°

BC² = ( 3 + x )² + 100 – 2.( 3 + x ).10.$\frac{1}{2}$ = x² + 6x + 9 + 100 – 30 – 10x

BC²  = x² – 4x + 79

Như vậy BC = $\sqrt{x^2–4x+79}$.

b) Ta có $AC=\frac{8}{9}BC$ 

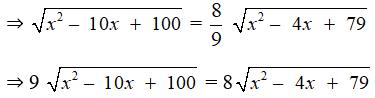
⇒ 81( x² – 10x + 100 ) = 64( x² – 4x + 79 )

⇒ 17x² – 554x + 3044 = 0

⇒ x ≈ 25,6 hoặc x ≈ 7

Vậy x ≈ 25,6 hoặc x ≈ 7.

c) Ta có BC = 2AN

⇒ $\sqrt{x^2–4x+79}$ = 2x

⇒ x² – 4x + 79 = 4x²

⇒ 3x² + 4x – 79 = 0

⇒ x ≈ 4,5 hoặc x ≈ –5,8 mà x > 0 nên x ≈ 4,5.

Vậy x ≈ 4,5 .

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giải bất phương trình bậc hai một ẩn

Bài tập cuối chương 7

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp