20 câu Trắc nghiệm Tập hợp (Kết nối tri thức 2023) có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Bài 2: Tập hợp

I. Nhận biết

Câu 1. Cho các tập hợp:

A = {x ∈ ℤ | -1 < x < 6};

B = {x ∈ ℤ | 0 ≤ x ≤ 1}.

Xác định A\B. Câu nào sau đây đúng?

A. A\B = {2; 3; 4};

B. A\B = {2; 3; 4; 5};

C. A\B = {2; 3};

D. A\B = {3; 4; 5}.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có:

+ Các phần tử của tập hợp A là 0; 1; 2; 3; 4; 5.

⟹ A = {0; 1; 2; 3; 4; 5}.

+ Các phần tử của tập hợp B là 0; 1.

⟹ B = {0; 1}.

Các phần tử thuộc A mà không thuộc B là 2; 3; 4; 5.

⟹ A\B = {2; 3; 4; 5}.

Câu 2. Cho các tập hợp:

A = {x ∈ ℤ | 1 < x < 4};

B = {x ∈ ℤ | 3 < x < 5}.

Xác định tập hợp X = A ∪ B.

A. X = {2; 3; 4};

B. X = {3; 4};

C. X = {2; 3};

D. X = {1; 2; 3}.

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có:

+ Tập hợp A gồm các phần tử là 2; 3.

⟹ A = {2; 3}.

+ Tập hợp B gồm phần tử là 4.

⟹ B = {4}.

Hợp của hai tập hợp trên là các phần tử thuộc tập hợp này hoặc tập hợp kia nên ta có tập hợp A gồm có các phần tử là {2; 3; 4}.

⟹ X = {2; 3; 4}.

Câu 3. Tập hợp X = {x ∈ ℤ | 2 < x < 5} bằng tập hợp nào sau đây?

A. A = {3; 4};

B. B = {2; 3; 4; 5};

C. C = {3; 4; 5};

D. D = {2; 3; 4}.

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có: 2 < x < 5

Mà x ∈ ℤ nên x nhận các giá trị là 3 ; 4.

⟹ X = {3; 4}.

Vậy X = A.

Câu 4. Cho tập hợp B gồm các số tự nhiên bé hơn 20 và chia hết cho 4.

Viết tập hợp trên dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.

A. B = {x ∈ ℤ | x ≤ 20 và x ⋮ 4};

B. B = {x ∈ ℤ | x < 20 và x ⋮ 4};

C. B = {x ∈ ℕ | x ≤ 20 và x ⋮ 4};

D. B = {x ∈ ℕ | x < 20 và x ⋮ 4}.

Hướng dẫn giải

Đáp án: D

Giải thích:

Gọi x là phần tử bất kì thuộc tập hợp B

+ Tập hợp B gồm các số tự nhiên nên x ∈ ℕ.

+ Tập hợp B gồm các số tự nhiên bé hơn 20 và chia hết cho 4 nên x < 20 và x ⋮ 4.

 Do đó tập hợp trên được viết dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó như sau:

B = {x ∈ ℕ | x < 20 và x ⋮ 4}.

Câu 5. Cho tập hợp E = {x ∈ ℕ | x là ước chung của 20 và 40}.

Tập hợp E có bao nhiêu phần tử?

A. 4;

B. 5;

C. 3;

D. 2.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có:

+ Các ước là số tự nhiên của 20 là: 1; 2; 4; 5; 10; 20.

+ Các ước là số tự nhiên của 40 là: 1; 2; 4; 5; 8; 10; 20; 40.

Do đó các ước chung là số tự nhiên của 20 và 30 là 1; 2; 5; 10; 20.

⟹ E = {1; 2; 5; 10; 20}.

Vì vậy tập hợp E gồm có 5 phần tử.

⟹ n(E) = 5.

Câu 6. Cho các tập hợp : D = {1 ; 2 ; 3 ; 6 ; 9 ; 18} và E = {-1 ; 3 ; 5}. Phần tử nào dưới đây thuộc tập hợp E\D.

A. 2;

B. 9;

C. 3;

D. -1.

Hướng dẫn giải

Đáp án: D

Giải thích:

Các phần tử thuộc tập hợp E nhưng không thuộc tập hợp D là : – 1; 5.

⇒ E\D = {– 1; 5}.

Ta thấy chỉ có – 1 ∈ E\D.

Câu 7. Tập hợp B = {0; a; b} có bao nhiêu tập con?

A. 5;

B. 6;

C. 7;

D. 8.

Hướng dẫn giải

Đáp án: D

Giải thích:

Ta có:

+ Các tập con có 0 phần tử: ∅.

+ Các tập con có 1 phần tử: {0}, {a}, {b}.

+ Các tập con có 2 phần tử: {0; a}, {0; b}, {a; b}.

+ Các tập con có 3 phần tử: {0; a; b}.

⟹ Tập hợp A có 8 tập con.

II. Thông hiểu

Câu 8. Trong kì thi học sinh giỏi cấp trường, lớp 11B1 có 15 học sinh giỏi Văn, 22 học sinh giỏi Toán. Tìm số học sinh giỏi cả Văn và Toán biết lớp 11B1 có 40 học sinh, và có 14 học sinh không đạt học sinh giỏi.
A. 4;

B. 7;

C. 11;

D. 20. 

Hướng dẫn giải

Đáp án: C

Giải thích:

 

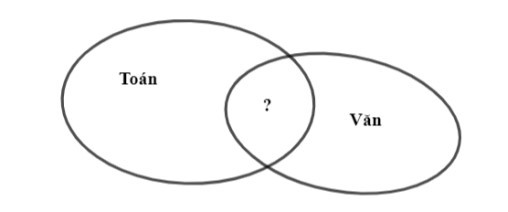
Số học sinh học giỏi ít nhất một trong hai môn Toán và Văn là: 40 – 14 = 26.
Số học sinh chỉ giỏi Toán mà không giỏi Văn (Phần Toán sau khi bỏ đi phần giao)
là: 26 – 15 = 11.
Vậy số học sinh giỏi cả hai môn Toán và Văn (Phần giao nhau) là: 22 – 11 = 11 (học sinh). 

Câu 9. Cho tập hợp A = [4; 7] và B = [2a + 3b – 1; 3a – b + 5] với a, b ∈ ℝ. Khi A = B thì giá trị của biểu thức M = a² + b² bằng?

A. 2;

B. 5;

C. 13;

D. 25.

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có:

A = [4; 7], B = [2a + 3b – 1; 3a – b + 5] với a, b ∈ ℝ.

Khi đó:

A = B ⇔ 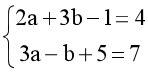⟺ ⟺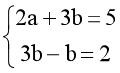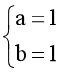⟹ M = a² + b² = 2.

Câu 10. Tập hợp C = {x ∈ ℤ | (x² – 5x + 4)(x² 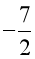x + 3) = 0} có bao nhiêu phần tử?

A. n(C) = 2;

B. n(C) = 3;

C. n(C) = 4;

D. n(C) = 5;

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có:

(x² – 5x + 4)(x² 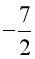x + 3) = 0

⟺  ⟺ .

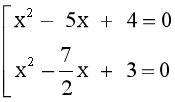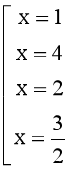Vì x ∈ ℤ nên ta loại nghiệm .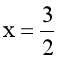

⟹ C = {1; 2; 4}.

⟹ n(C) = 3.

Câu 11. Cho ba tập hợp sau:

A = {m + 1; 2}

B = {1; n – 3}

C = {t; 2}

Hỏi m, n, t nhận giá trị nào sau đây thì A = B = C?

A. m = 1, n = 1, t = 1;

B. m = – 1, n = 5, t = 1;

C. m = 0, n = 5, t = 1;

D. m = 0, n = 5, t = – 1.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta thấy tập hợp A có 2 phần tử là m + 1 và 2.

Mà tập hợp B có 2 phần tử là 1 và n – 3.

Do đó để A = B thì .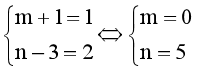

Ta lại có tập hợp C có 2 phần tử là t và 2.

Do đó để B = C thì t = 1.

Vậy để A = B = C thì m = 0, n = 5, t = 1.

Câu 12. Cho tập hợp B = {x ∈ ℕ| 3 < 2x – 1 < m}.

Tìm giá trị của m để B là tập hợp rỗng?

A. m = 7;

B. m = 5;

C. m = 9;

D. m = 8.

Hướng dẫn giải

Đáp án: B

Giải thích:

Xét bất phương trình 3 < 2x – 1 < m (*).

A. Thay m = 7 vào bất phương trình (*) ta có:

3 < 2x – 1 < 7

⟺ 3 + 1 < 2x < 7 + 1

⟺ 4 < 2x < 8

⟺ 2 < x < 4.

Vì x ∈ ℕ nên ta nhận giá trị x = 3.

⟹ m = 7 thì A = {3}.

B. Thay m = 5 vào bất phương trình (*) ta có:

3 < 2x – 1 < 5

⟺ 3 + 1 < 2x < 5 + 1

⟺ 4 < 2x < 6

⟺ 2 < x < 3.

Vì x ∈ ℕ nên không có giá trị của x nào thỏa mãn.

⟹ m = 5 thì B = ∅.

C. Thay m = 9 vào bất phương trình (*) ta có:

3 < 2x – 1 < 9

⟺ 3 + 1 < 2x < 9 + 1

⟺ 4 < 2x < 10

⟺ 2 < x < 5.

Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.

⟹ m = 7 thì A = {3; 4}.

D. Thay m = 8 vào bất phương trình (*) ta có:

3 < 2x – 1 < 8

⟺ 3 + 1 < 2x < 8 + 1

⟺ 4 < 2x < 9

⟺ 2 < x < .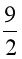

Vì x ∈ ℕ nên ta nhận giá trị x = 3 và x = 4.

⟹ m = 7 thì A = {3; 4}.

Vậy m = 5 thì B là tập hợp rỗng.

Câu 13. Trong các tập hợp sau, tập hợp nào không phải là tập hợp rỗng?

A. A = {x ∈ ℕ | x² + x + 3 = 0};

B. B = {x ∈ ℕ | x² + 6x + 5 = 0};

C. C = {x ∈ ℕ* | x(x² – 5) = 0};

D. D = {x ∈ ℕ* | x² – 9x + 20 = 0}.

Hướng dẫn giải

Đáp án: D

Giải thích:

A. Ta có:

Phương trình x² + x + 3 = 0 vô nghiệm.

⟹ Tập hợp A không có phần tử nào thỏa mãn.

⟹ C = ∅.

B. Ta có:

x² + 6x + 5 = 0 ⟺ .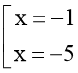

Vì x ∈ ℕ* nên không có phần tử nào thỏa mãn tập hợp trên.

⟹ B = ∅.

C. Ta có:

x(x² – 5) = 0 ⟺  ⟺ .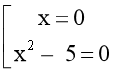

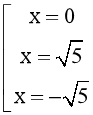Vì x ∈ ℕ nên không có phần tử nào thỏa mãn tập hợp trên.

⟹ C = ∅.

D. Ta có:

x² – 9x + 20 = 0 ⟺ .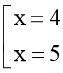

Vì x ∈ ℕ*  nên hai nghiệm x = 4 và x = 5 đều thỏa mãn.

Do đó tập hợp D có hai phần tử.

⟹ D = {4; 5}.

Vậy chỉ có tập hợp D không phải là tập hợp rỗng.

Câu 14. Cho các tập hợp:

A = {x ∈ ℤ | -4 ≤ x ≤ 5};

B = {x ∈ ℤ | -2 ≤ x ≤ 6};

C = {x ∈ ℤ | 0 ≤ x ≤ 1}.

Xác định tập hợp X = (A ∩ B)\C. Câu nào sau đây đúng?

A. X = {-1; 2; 3; 4; 5};

B. X = {2; 3; 4; 5};

C. X = {-2; -1; 2; 3; 4; 5};

D. X = {-2; -1; 2; 3; 4}.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta có:

+ Các phần tử của tập hợp A là -4; -3; -2; -1; 0; 1; 2; 3; 4; 5.

⟹ A = {-4; -3; -2; -1; 0; 1; 2; 3; 4; 5}.

+ Các phần tử của tập hợp B là -2; -1; 0; 1; 2; 3; 4; 5; 6.

⟹ B = {-2; -1; 0; 1; 2; 3; 4; 5; 6}.

+ Các phần tử của tập hợp C là 0; 1.

⟹ C = {0; 1}.

– Giao của hai tập hợp A và B là tập hợp các phần tử thuộc tập hợp A cũng thuộc tập hợp B, do đó các phần tử thuộc tập hợp A ∩ B là -2; -1; 0; 1; 2; 3; 4; 5.

⟹ A ∩ B = {-2; -1; 0; 1; 2; 3; 4; 5}.

– Các phần tử thuộc tập hợp A ∩ B mà không thuộc tập hợp C là -2; -1; 2; 3; 4; 5.

⟹ X = (A ∩ B)\C = {-2; -1; 2; 3; 4; 5}.

Câu 15. Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B1 là: 

A. 9;

B. 10; 

C. 18;

D. 28.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta dùng biểu đồ Ven để giải: 

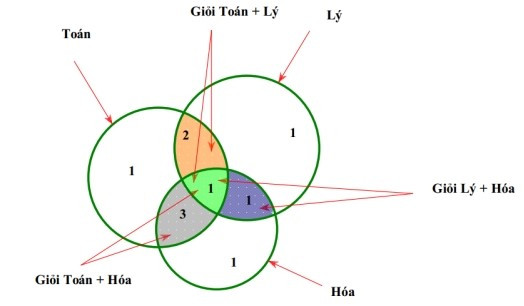
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là: 1+ 2 + 1 + 3 + 1 + 1 + 1 = 10.

III. Vận dụng

Câu 1. Cho A = {x ∈ ℝ | |x – m| ≤ 25}; B = {x ∈ ℝ | |x| ≥ 2020}.

Có bao nhiêu giá trị nguyên m thỏa mãn A ∩ B = ∅.

A. 3987;

B. 3988;

C. 3989;

D. 2020.

Hướng dẫn giải

Đáp án: C

Giải thích:

Ta có:

A = {x ∈ ℝ | |x – m| ≤ 25} ⟹ A = [m – 25; m + 25]

B = {x ∈ ℝ | |x| ≥ 2020} ⟹ B = (-∞; -2020] ∪ [2020; +∞)

Để A ∩ B = ∅ thì -2020 < m – 25 và m + 25 < 2020 (1)

Khi đó (1) ⟺ 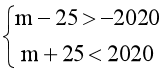 ⟺ 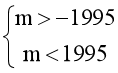 ⟹ -1995 < m < 1995.

Vậy có 3989 giá trị nguyên m thỏa mãn.

Câu 2. Lớp 10A có 40 học sinh trong đó có 10 bạn học sinh giỏi Toán, 15 bạn học sinh giỏi Lý và 19 bạn không giỏi môn học nào trong hai môn Toán, Lý. Hỏi lớp 10A có bao nhiêu bạn học sinh vừa giỏi Toán vừa giỏi Lý?
A. 7;

B. 10;

C. 4;

D. 17 .

Hướng dẫn giải

Đáp án: C

Giải thích:

 

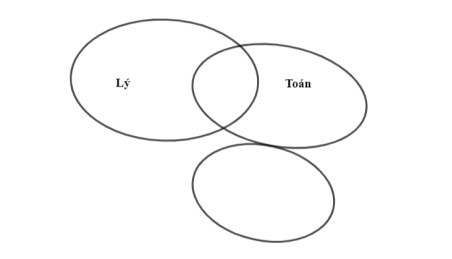
Số học sinh giỏi Toán hoặc Lý là:
40 – 19 = 21 (học sinh)
Số học sinh chỉ giỏi một môn Lý là:
21 – 10 = 11 (học sinh)
Số học sinh chỉ giỏi một môn Toán là:
21 – 15 = 6 (học sinh)
Số học sinh giỏi cả hai môn là:
21 – 11 – 6 = 4 (học sinh) .

Câu 3. Cho hai tập hợp P = [3m – 6; 4] và Q = (-2; m + 1), m ∈ ℝ. Tìm m để

P\Q = ∅.

A. 3 ≤ m < ;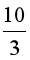

B. 3 < m < ;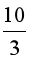

C. m ≥ 3;

D. 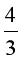< m ≤ 3.

Hướng dẫn giải

Đáp án: A

Giải thích:

Vì P, Q là hai tập hợp khác rỗng nên ta có điều kiện:

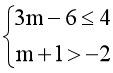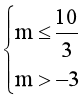⟺ ⟺ -3 < m ≤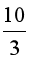 

Để P\Q = ∅ ⟺ P ⊂ Q

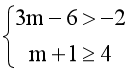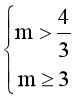⟺ ⇔ m ≥ 3

Kết hợp với điều kiện ta có 3 ≤ m ≤ .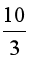

Câu 4. Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
A. 20; 

B. 45; 

C. 38; 

D. 21. 

Hướng dẫn giải

Đáp án: D

Giải thích:

 

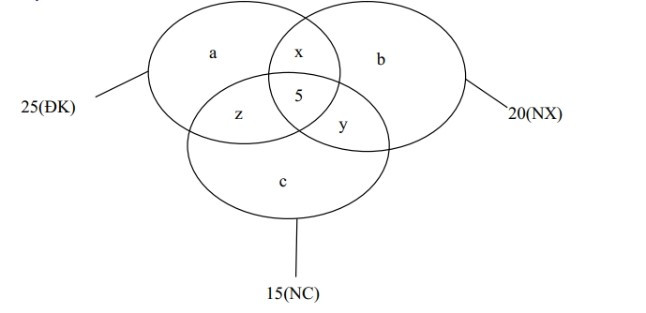
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hai môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: 45 –  7 = 38
Dựa vào biểu đồ ven ta có hệ phương trình sau: 

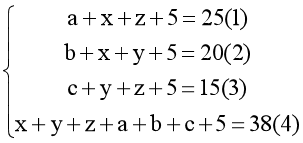
Cộng vế với vế của (1), (2), (3) ta có: a + b + c + 2(x + y + z) + 15 = 60 (5)

Từ (4) và (5) ta có: a + b + c + 2(38 – 5 – a – b – c) + 15 = 60

⟺ a + b + c = 21.

Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.

Câu 5. Cho tập M = {(x; y) | x, y ∈ ℝ và x² + y² ≤ 0}. Hỏi tập M có bao nhiêu phần tử?

A. 0;

B. 1;

C. 2;

D. Vô số.

Hướng dẫn giải

Đáp án: B

Giải thích:

Ta có:

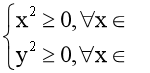 ⟹ x² + y² ≥ 0.

Mà x² + y² ≤ 0 nên chỉ xảy ra khi x² + y² = 0 ⟺ x = y = 0.

Do đó ta suy ra M = {(0; 0)} nên M có 1 phần tử.

Xem thêm các bài trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Trắc nghiệm Bài 1: Mệnh đề

Trắc nghiệm Bài 2: Tập hợp

Trắc nghiệm Ôn tập cuối chương 1

Trắc nghiệm Bài 3: Bất phương trình bậc nhất hai ẩn

Trắc nghiệm Bài 4: Hệ bất phương trình bậc nhất hai ẩn