Trắc nghiệm Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn
I. Nhận biết
Câu 1. Bất phương trình nào sau đây không là bất phương trình bậc nhất hai ẩn
A. x + 2y > 1;
B. – x + 3 < –y;
C. 3x + y + 1 ≤ 0;
D. 2x + y2 > 2.
Hướng dẫn giải
Đáp án: D
Giải thích:
Đáp án D: 2x + y2 > 2 không là bất phương trình bậc nhất hai ẩn vì chứa y2.
Câu 2. Cho bất phương trình 2x – 3y + 6 ≥ 0. Chọn khẳng định đúng trong các khẳng định sau:
A. Bất phương trình chỉ có một nghiệm duy nhất.
B. Bất phương trình vô nghiệm.
C. Bất phương trình luôn có vô số nghiệm.
D. Bất phương trình có tập nghiệm là ℝ.
Hướng dẫn giải
Đáp án: C
Giải thích:
Trên mặt phẳng tọa độ, đường thẳng 2x – 3y + 6 = 0. chia mặt phẳng thành hai nửa mặt phẳng.
Chọn điểm O(0; 0) không thuộc đường thẳng đó, có: 2.0 – 3.0 + 6 = 6 > 0. Ta thấy (0; 0) là nghiệm của bất phương trình đã cho. Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O(0; 0) kể cả bờ.
Vậy bất phương trình luôn có vô số nghiệm.
Câu 3. Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình x + 2y < 1
A. (– 2; 1);
B. (3; – 7);
C. (0; 1);
D. (0; 0).
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét đáp án A: – 2 + 2.1 = 0 < 1, đáp án A là nghiệm của bất phương trình.
Xét đáp án B: 3 + 2.(– 7) = – 11 < 1, đáp án B là nghiệm của bất phương trình.
Xét đáp án C: 0 + 2.1 = 2 > 1, đáp án C không là nghiệm của bất phương trình.
Xét đáp án D: 0 + 2.0 = 0 < 1, đáp án D là nghiệm của bất phương trình.
Câu 4. Cặp số (0; – 3) là nghiệm của bất phương trình nào sau đây?
A. x + y – 3 > 0;
B. – x – y < 0;
C. x + 3y + 1 < 0;
D. – x – 3y – 1 < 0.
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét đáp án A: 0 + (– 3) – 3 = – 6 < 0, đáp án A không là nghiệm của bất phương trình.
Đáp án B: – 0 – (– 3) = 3 > 0, đáp án B không là nghiệm của bất phương trình.
Đáp án C: 0 + 3.( – 3) + 1= – 8 < 0, đáp án C là nghiệm của bất phương trình.
Đáp án D: – 0 – 3(– 3) – 1 = 8 > 0, đáp án D không là nghiệm của bất phương trình.
Câu 5. Trong các cặp số sau đây: (– 5; 0); (– 2; 1); (– 1; 3); (– 7; 0). Có bao nhiêu cặp số là nghiệm của bất phương trình x – 4y + 5 ≥ 0?
A. 0;
B. 1;
C. 3;
D. 4.
Hướng dẫn giải
Đáp án: B
Giải thích:
Xét đáp án A: – 5 – 4.0 + 5 = 0, vậy (– 5; 0) là nghiệm của bất phương trình.
Đáp án B: – 2 – 4.1 + 5 = – 1 < 0, vậy (– 2; 1) không là nghiệm của bất phương trình.
Đáp án C: – 1 – 4.3 + 5 = – 8 < 0, vậy (– 1; 3) không là nghiệm của bất phương trình.
Đáp án D: – 7 – 4.0 + 5 = – 2 < 0, vậy (–7; 0) không là nghiệm của bất phương trình.
Vậy có 1 cặp số là nghiệm của bất phương trình.
Câu 6. Bất phương trình nào say đây là bất phương trình bậc nhất hai ẩn
A. x + 2y = 5;
B. 3x2 – 2y > 0;
C. x – y + 1 ≥ 0;
D. 2x + y2 – 3 < 0.
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét đáp án A: x + 2y = 5 là phương trình bậc nhất hai ẩn nên không phải là bất phương trình bậc nhất hai ẩn.
Xét đáp án B: 3x2 – 2y > 0 không là bất phương trình bậc nhất hai ẩn vì có chứa x2.
Xét đáp án C: x – y + 1 ≥ 0 là bất phương trình bậc nhất hai ẩn.
Xét đáp án D: 2x + y2 – 3 < 0 không là bất phương trình bậc nhất hai ẩn vì chứa y2.
Câu 7. Bất phương trình x – 2(y – x + 1) > 0 tương đương với bất phương trình nào sau đây?
A. 3x – y – 2 > 0;
B. 3x – 2y + 2 > 0;
C. 3x – 2y + 1 > 0;
D. 3x – 2y – 2 > 0.
Hướng dẫn giải
Đáp án: D
Giải thích:
x – 2(y – x + 1) > 0 x – 2y + 2x – 2 > 0 3x – 2y – 2 > 0
Vậy đáp án đúng là D
II. Thông hiểu
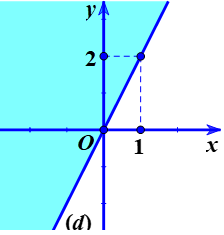
Câu 8. Phần tô đậm trong hình vẽ dưới đây (kể cả đường thẳng d) biểu diễn miền nghiệm của bất phương trình.
A. – 2x + y ≥ 0;
B. 2x + y ≥ 0;
C. – 2x – y ≥ 1;
D. x + 2y ≥ 0.
Hướng dẫn giải
Đáp án: A
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng: y = ax + b. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (0; 0) và (1; 2). Ta có hệ phương trình:
y = 2x.
Suy ra đường thẳng có phương trình – 2x + y = 0.
Xét điểm A(0; 2) thuộc vào phần tô màu thay vào phương trình đường thẳng ta được: – 2.0 + 2 = 2 > 0.
Vì điểm A(0; 2) thuộc miền nghiệm của bất phương trình. Vậy phần tô đậm biểu diễn miền nghiệm của bất phương trình – 2x + y ≥ 0 (kể cả đường thẳng d).
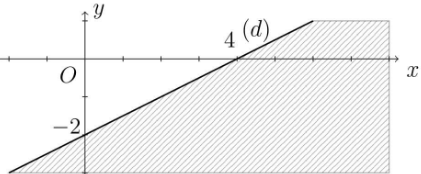
Câu 9. Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình nào?
A. – x + 2y > 2;
B. 2x – y > – 4;
C. 2x – y > 2;
D. – x + 2y > – 4.
Hướng dẫn giải
Đáp án: D
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = ax + b. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (4; 0) và (0; – 2). Ta có hệ phương trình
y = x – 2
Suy ra đường thẳng d có phương trình – x + 2y = – 4.
Xét điểm O(0; 0), ta có: – 0 + 2.0 = 0 > – 4.
Vì O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) biểu diễn miền nghiệm của bất phương trình – x + 2y > – 4.
Câu 10. Có bao nhiêu giá trị nguyên dương của m để cặp số (– 2m; 1) là nghiệm của bất phương trình 2x – y – 3 > 0?
A. 0;
B. 1;
C. 2;
D. Vô số.
Hướng dẫn giải
Đáp án: A
Giải thích:
Vì cặp số (– 2m; 1) là nghiệm của bất phương trình 2x – y – 3 > 0, nên ta có:
2.( – 2m) – 1 – 3 = – 4m – 4 > 0 ⇔ m < – 1
Mà m là số nguyên dương nên không tồn tại giá trị của m thỏa mãn điều kiện của phương trình.
Câu 11. Nửa mặt phẳng là miền nghiệm của bất phương trình – x + 2 + 2(y – 2) < 2(1 – x) chứa điểm nào trong các điểm sau:
A. (0; 3);
B. (2; 1);
C. (4; 2);
D. (1; – 1).
Hướng dẫn giải
Đáp án: D
Giải thích:
Ta có: – x + 2 + 2(y – 2) < 2(1 – x) – x + 2 + 2y – 4 < 2 – 2x x + 2y < 4.
Xét điểm (0; 3), có: 0 + 2.3 = 6 > 4, không thoả mãn bất phương trình x + 2y < 4, vậy điểm (0; 3) không thuộc miền nghiệm của bất phương trình, đáp án A sai.
Xét điểm (2; 1), có: 2 + 2.1 = 4, không thoả mãn bất phương trình x + 2y < 4, vậy điểm (2; 1) không thuộc miền nghiệm của bất phương trình, đáp án B sai.
Xét điểm (4; 2), có: 4 + 2.2 = 8 > 4, không thoả mãn bất phương trình x + 2y < 4, vậy điểm (4; 2) không thuộc miền nghiệm của bất phương trình, đáp án C sai.
Xét điểm (1; – 1), có: 1 + 2.( – 1) = – 1 < 4, thoả mãn bất phương trình x + 2y < 4, vậy điểm (1; – 1) thuộc miền nghiệm của bất phương trình, đáp án D đúng.
Câu 12. Miền nghiệm của bất phương trình 4(x – 1) + 5(y – 3) > 2x – 9 là nửa mặt phẳng không chứa điểm nào sau đây
A. (0; 3);
B. (1; 2);
C. (- 1; 1);
D. (2; 5)
Hướng dẫn giải
Đáp án: C
Giải thích:
Ta có: 4(x – 1) + 5(y – 3) > 2x – 9 4x – 4 + 5y – 15 > 2x – 9 2x + 5y > 10.
Xét điểm (0; 3), có: 2.0 + 5.3 = 15 > 10 thoả mãn bất phương trình 2x + 5y > 10, vậy điểm (0; 3) thuộc miền nghiệm của bất phương trình, đáp án A sai.
Xét điểm (1; 2), có: 2.1 + 5.2 = 12 > 10 thoả mãn bất phương trình 2x + 5y > 10, vậy điểm (1; 2) thuộc miền nghiệm của bất phương trình, đáp án B sai.
Xét điểm (–1; 1), có: 2.(– 1) + 5.1 = 3 < 10 không thoả mãn bất phương trình 2x + 5y > 10, vậy điểm (–1; 1) không thuộc miền nghiệm của bất phương trình, đáp án C đúng.
Xét điểm (2; 5), có: 2.2 + 5.5 = 29 > 10 thoả mãn bất phương trình 2x + 5y > 10, vậy điểm (2; 5) thuộc miền nghiệm của bất phương trình, đáp án D sai.
Câu 13. Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?
A. 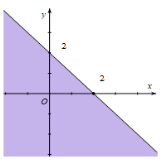
B.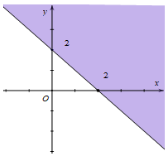
C.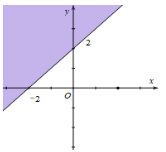
D.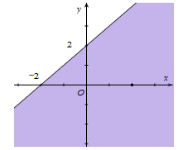
Hướng dẫn giải
Đáp án: A
Giải thích:
Xét đường thẳng x + y – 2 = 0 đi qua 2 điểm A(2; 0) và B(0; 2). Lấy điểm O(0; 0) ta có: 0 + 0 = 0 < 2. Vậy miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng có bờ là đường thẳng x + y – 2 = 0 và có chứa điểm O cũng chính là phần tô đậm ở đáp án A.
Câu 14. Miền nghiệm của bất phương trình 3(x – 1) + 4(y – 2) < 5x – 3 là phần không bị gạch của hình vẽ nào, trong các hình vẽ sau (không kể bờ)?
A.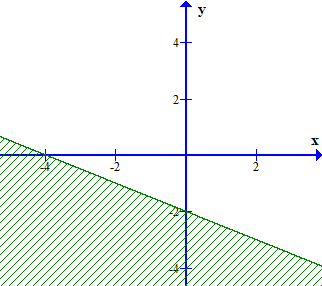
B.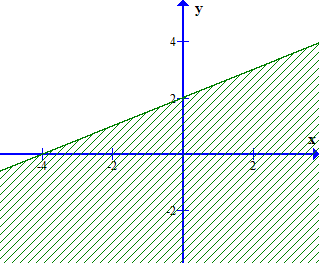
C.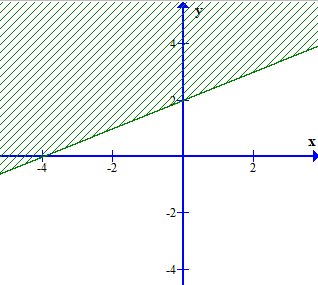
D.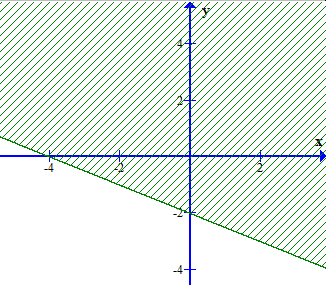
Hướng dẫn giải
Đáp án: C
Giải thích:
Ta có: 3(x – 1) + 4(y – 2) < 5x – 3 3x – 3 + 4y – 8 < 5x – 3 – 2x + 4y < 8
Xét đường thẳng – 2x + 4y – 8 = 0 đi qua 2 điểm A(– 4; 0) và B(0; 2). Lấy điểm O(0; 0) ta có: – 2.0 + 4.0 = 0 < 8. Vậy miền nghiệm của bất phương trình – 2x + 4y < 8 là phần không bị gạch ở đáp án C.
Câu 15. Miền nghiệm của bất phương trình 3x + 2(y + 3) ≥ 4(x + 1) – y + 3 là phần không bị gạch của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?
A.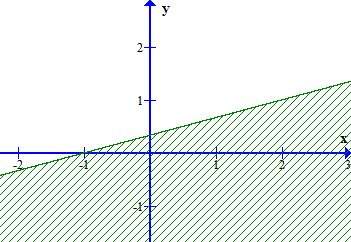
B.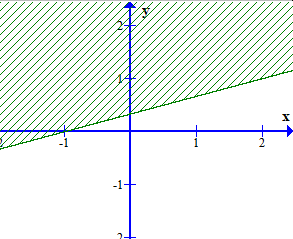
C.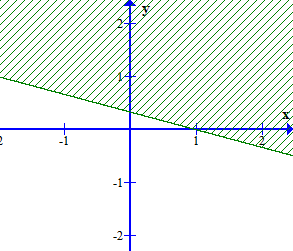
D.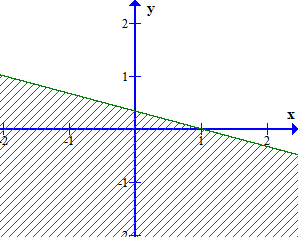
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta có: 3x + 2(y + 3) > 4(x + 1) – y + 3 3x + 2y + 6 > 4x + 4 – y + 3 – x + 3y > 1
Xét đường thẳng – x + 3y – 1 = 0 đi qua 2 điểm A(– 1; 0) và B . Lấy điểm O(0; 0) ta có: – 0 + 3.0 = 0 < 1. Vậy miền nghiệm của bất phương trình – x + 3y > 1 là phần không bị gạch ở đáp án A.
III. Vận dụng
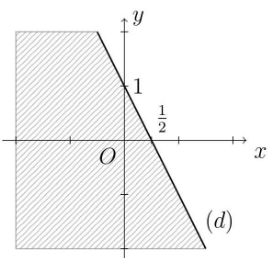
Câu 16. Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by > c. Tính giá trị của biểu thức P = a2 + b2 – 2c ?
A. P = 3;
B. P = 5;
C. P = 7;
D. P = 4.
Hướng dẫn giải
Đáp án: A
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là và (0; 1). Ta có hệ phương trình
y = – 2x + 1
Vậy đường thẳng có phương trình 2x + y = 1.
Xét điểm O(0; 0), có: 2.0 + 0 = 0 < 1.
Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + y > 1
Suy ra: a = 2; b = 1; c = 1
⇒ P = a2 + b2 – 2c = 22 + 12 – 2.1 = 3.
Vậy P = 3.
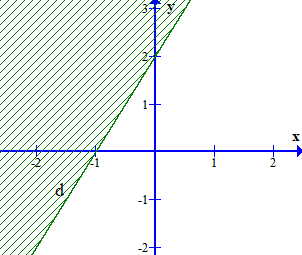
Câu 17. Phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (a – 1)x + (2b + 3)y > – 2. Giá trị của a, b là?
A. a = – 2; b = 1;
B. a = 2; b = – 1;
C. a = 3; b = – 2;
D. a = – 1; b = – 1.
Hướng dẫn giải
Đáp án: C
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (– 1; 0) và (0; 2). Ta có hệ phương trình
y = 2x + 2
Suy ra đường thẳng có phương trình – 2x + y = 2.
Xét điểm O(0; 0), có: – 2.0 + 0 = 0 < 2.
Vì O(0; 0) thuộc miền nghiệm của bất phương trình. Do đó phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình – 2x + y < 2 2x – y > – 2
Ta có a – 1 = 2 a = 3; 2b + 3 = – 1 b = – 2
Vậy a = 3 và b = – 2.
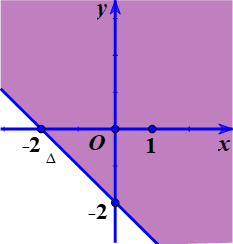
Câu 18. Phần nửa mặt phẳng tô đậm (không kể đường thẳng ∆) trong hình vẽ dưới đây biểu diễn miền nghiệm của bất phương trình ax + by > c. Hệ số a, c là nghiệm của hệ phương trình?
A. ;
B. ;
C. ;
D. .
Hướng dẫn giải
Đáp án: A
Giải thích:
Giả sử đường thẳng (∆) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = a’x + b’. Dễ dàng nhận thấy đường thẳng (∆) đi qua hai điểm có tọa độ là (– 2; 0) và (0; – 2). Ta có hệ phương trình
y = – x – 2
Vậy đường thẳng có phương trình x + y = – 2
Xét điểm O(0; 0), có: 0 + 0 = 0 > – 2.
Vì O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy phần tô đậm biểu diễn miền nghiệm của bất phương trình x + y > – 2 (không kề đường thẳng ∆)
Ta có a = 1; b = 1; c = – 2
Xét hệ phương trình A: .
Xét hệ phương trình B: .
Xét hệ phương trình C: .
Xét hệ phương trình D: .
Vậy chọn đáp án A.
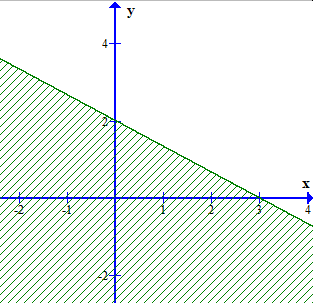
Câu 19. Phần nửa mặt phẳng không bị gạch (kể cả đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình ax + by ≥ c. Kết luận nào sau đây đúng?
A. a > b > c;
B. a < b < c;
C. b < a < c;
D. a < c < b.
Hướng dẫn giải
Đáp án: B
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = a’x + b’. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (3; 0) và (0; 2). Ta có hệ phương trình
y = x + 2 ⇔ 2x + 3y = 6
Suy ra đường thẳng d có phương trình 2x + 3y = 6.
Xét điểm O(0; 0), ta có: 2.0 + 3.0 = 0 < 6.
Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + 3y ≥ 6
Ta có a = 2; b = 3; c = 6
Suy ra a < b < c.
Vậy chọn đáp án B.
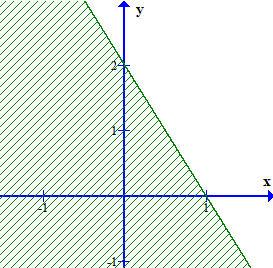
Câu 20. Có bao nhiêu giá trị của m để phần nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở hình dưới đây là miền nghiệm của bất phương trình (m2 – 3m + 2)x – y < – 2.
A. 0;
B. 1;
C. 2;
D. 3.
Hướng dẫn giải
Đáp án: C
Giải thích:
Giả sử đường thẳng (d) chia mặt phẳng tọa độ thành hai nửa mặt phẳng có dạng:
y = ax + b. Dễ dàng nhận thấy đường thẳng (d) đi qua hai điểm có tọa độ là (1; 0) và (0; 2). Ta có hệ phương trình
y = – 2x + 2
Vậy đường thẳng có phương trình 2x + y = 2.
Xét điểm O(0; 0), ta có: 2.0 + 0 = 0 < 2.
Vì O(0; 0) không thuộc miền nghiệm của bất phương trình. Vậy phần nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2x + y > 2 – 2x – y < – 2
Suy ra: m2 – 3m + 2 = – 2 ⇔ m2 – 3m + 4 = 0 có ∆ = (– 3)2 – 4.4 = – 7 < 0. Do đó phương trình vô nghiệm.
Vậy không có giá trị của m thoả mãn
Xem thêm các bài trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Trắc nghiệm Ôn tập cuối chương 1
Trắc nghiệm Bài 3: Bất phương trình bậc nhất hai ẩn
Trắc nghiệm Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Trắc nghiệm Ôn tập cuối chương 2
Trắc nghiệm Bài 5: Giá trị lượng giác của 1 góc từ 0° đến 180°