A. Ma trận
MA TRẬN ĐỀ THI HỌC KÌ II TOÁN 10
1. Trắc nghiệm: 50% – 20 câu × 0,25 = 5 điểm.
2. Tự luận: 50% – 4 bài tổng 5 điểm.
|
Chủ đề/chuẩn KTKN |
Cấp độ tư duy |
||||
|
Nhận biết |
Thông hiểu |
VD thấp |
VD cao |
Cộng |
|
|
1. Bất phương trình và hệ bất phương trình bậc nhất Biết tìm được tập nghiệm của bpt hoặc hệ bpt bậc nhất |
1 |
|
|
|
1 |
|
2. Nhị thức- bpt và hệ bpt bậc nhất 2 ẩn Biết xét dấu nhị thức, hiểu được điểm thuộc miền nghiệm của hệ bpt bậc nhất 2 ẩn |
1 |
1 |
|
|
2 |
|
3. Tam thức bậc hai, bpt bậc hai Biết được định lí dấu tam thức bậc hai, hiểu và tìm được tập nghiệm của bpt bậc hai một ẩn, vận dụng định lí dấu tam thức để tìm giá trị tham số thỏa điều kiện cho trước |
1 |
1 |
1 TL |
1
|
3 1 TL |
|
4. Thống kê Biết được số trung bình cộng, phương sai, độ lệch chuẩn của mẫu số liệu |
1 |
|
|
|
1 |
|
5. Góc và cung lượng giác Biết được dấu của các giá trị lượng giác |
1 |
|
|
|
1 |
|
6. Giá trị lượng giác của cung (góc) và cung (góc) liên quan đặc biệt Biết công thức lượng giác cơ bản, giá trị lượng giác của các cung(góc) liên quan đặc biệt và vận dụng được để tính giá trị biểu thức lượng giác |
1 |
1 |
1 0,5 TL |
0,5 TL |
3 TN 1 TL |
|
7. Công thức lượng giác Biết và hiểu được các công thức lượng giác |
1 |
1 |
|
|
2 |
|
8. Phương trình đường thẳng Biết các khái niệm vectơ pháp tuyến, vectơ chỉ phương và viết được phương trình đường thẳng khi biết một số yếu tố |
1 |
1 |
1 TL |
1 |
3 TN 1 TL |
|
9. Phương trình đường tròn Biết khái niệm phương trình đường tròn, phương trình tiếp tuyến của đường tròn và tìm được tâm, bán kính của đường tròn cho trước |
1 |
1 |
1 |
1 TL |
3 TN 1 TL |
|
10. Phương trình Elip Biết phương trình chính tắc và hình dạng của Elip |
1 |
|
|
|
1 |
|
Tổng |
10 TN |
6 TN |
2 + 2,5 TL |
2 + 1,5 TL |
20 TN + 4 TL |
B. Đề bài
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 1)
A. Phần trắc nghiệm: Khoanh tròn vào phương án đúng.
Câu 1: Trong các công thức sau, công thức nào sai ?
A. \[\sin 2a = 2\cos a.\sin a;\]
B. \[\cos 2a = {\cos ^2}a – {\sin ^2}a;\]
C. \[\cos 2a = 2{\cos ^2}a–1;\]
D. \[{\cos ^2}a = 1–2{\sin ^2}a.\]
Câu 2: Tìm mệnh đề đúng?
A.\[\;a < b \Rightarrow \;ac < bc\];
B.\(a < b \Rightarrow \frac{1}{a} > \frac{1}{b};\)
C.\(a < b\) và \(c < d \Rightarrow ac < bd\);
D.\[\;a < b \Rightarrow \;ac < bc,\left( {c > 0} \right)\].
Câu 3: Tập nghiệm bất phương trình \(\left\{ \begin{array}{l}2x – 3 > x + 1\\3x + 2 < 2x + 7\end{array} \right.\) là:
A. \(S = \left( { – 4;5} \right)\)
B. \(S = \left( {4;5} \right)\);
C. \(S = \left( { – 4;9} \right)\);
D. \(S = \left( { – 3;2} \right)\) .
Câu 4: Tập nghiệm của bất phương trình \({\left( {x + 2} \right)^2}\left( {x – 2} \right) \ge 0\) là:
A. \(S = \left( { – \infty ;2} \right)\);
B. \[S = \left[ {2; + \infty } \right)\];
C. \(S = \left[ { – 2; + \infty } \right.)/\left\{ 2 \right\}\);
D.\[S = \left[ {2; + \infty } \right) \cup \left\{ { – 2} \right\}\].
Câu 5: Cho phương trình \[{x^2} + 2x – m + 2 = 0\]\[\left( 1 \right)\]. Với giá trị nào của m thì (1) có 2 nghiệm \[{x_1} < {x_2} < 0\].
A. \[m > 2\];
B. \[m < – 2\];
C. \[m < – 2\];
D. \[m < 2\].
Câu 6: Cho mẫu số liệu 10, 8, 6, 2, 4. Tính độ lệch chuẩn (làm tròn kết quả đến hàng phần mười).
A. 2,8;
B. 2,4;
C. 6,0;
D. 8,0.
Câu 7: Điểm kiểm tra học kì môn Toán của các học sinh lớp 10A cho ở bảng dưới đây.
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Tần số |
1 |
2 |
5 |
8 |
6 |
10 |
7 |
2 |
Tính phương sai của dãy điểm trên?
A. 40;
B. 39;
C. 41;
D. 42.
Câu 8: Tam thức\(y = – {x^2} + 2x\) nhận giá trị âm khi chỉ khi:
A. \(\left[ \begin{array}{l}x < 0\\x > 2\end{array} \right.\) ;
B. \(\left[ \begin{array}{l}x < 2\\x > 0\end{array} \right.\) ;
C. \(0 < x < 2\);
D. \( – 2 < x < 0\) \[ – 1 < x < 8\].
Câu 9: Tập nghiệm của bất phương trình \({x^2} > 16\) là:
A.\(S = \left( { – 4;4} \right)\);
B. \(S = \left( { – \infty ;4} \right)\);
C. \(S = \left( { – \infty ; – 4} \right)\);
D. \(S = \left( { – \infty , – 4} \right) \cup \left( {4; + \infty } \right)\).
Câu 10: Trong các công thức sau, công thức nào sai ?
A. \[\cos x\cos y = \frac{1}{2}\left[ {\cos \left( {x–y} \right) + \cos \left( {x + y} \right)} \right];\]
B. \[\sin x\sin y = \frac{1}{2}\left[ {\cos \left( {x–y} \right)–\cos \left( {x + y} \right)} \right];\]
C. \[\sin x\cos y = \frac{1}{2}\left[ {\sin \left( {x–y} \right) – \sin \left( {x + y} \right)} \right];\]
D. \[\sin x\cos y = \frac{1}{2}\left[ {\sin \left( {x – y} \right) + sin\left( {x + y} \right)} \right].\]
Câu 11: Góc có số đo \(\frac{\pi }{{15\,}}\,rad\) đổi sang độ là:
A. 12°;
B. 18°;
C. 5°;
D. 10°.
Câu 12: Véctơ nào sau đây là một véctơ chỉ phương của đường thẳng \[ – x + 3y + 2 = 0\]?
A. \(\overrightarrow {{u_1}} = \left( { – 1;3} \right)\);
B. \(\overrightarrow {{u_2}} = \left( {3;1} \right)\);
C. \(\overrightarrow {{u_3}} = \left( { – 3;1} \right)\);
D. \(\overrightarrow {{u_4}} = \left( {1;3} \right)\).
Câu 13: Tính khoảng cách d từ điểm A(1; 2) đến đường thẳng \[\Delta :12x + 5y + 4 = 0\].
A. d = 2;
B. \(d = \frac{{13}}{{17}}\);
C. d = 4;
D. \(d = \frac{{11}}{{12}}\).
Câu 14: Viết phương trình đường tiếp tuyến với \[\left( C \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} = 13\] biết tiếp tuyến song song với đường thẳng \[d:\,\,2x – 3y – 5 = 0\].
A. \( – 2x + 3y – 16 = 0\);
B. \( – 2x + 3y + 15 = 0\);
C. \(2x – 3y + 10 = 0\);
D. \(2x – 3y + 5 = 0\).
Câu 15: Biết \[\sin \,\alpha \, + \cos \,\alpha = \frac{7}{5}\]. Trong các kết quả sau, kết quả nào sai ?
A.\(\sin \,\alpha \,.\,\cos \,\alpha \, = \,\frac{{12}}{{25}}\);
B.\(\sin \,\alpha \, – \cos \,\alpha \, = \, \pm \frac{{\sqrt {35} }}{6}\);
C. \(\sin {\,^4}\alpha \, + \,{\cos ^4}\,\alpha \, = \frac{{337}}{{625}}\);
D. \({\tan ^2}\alpha \, + \,{\cot ^2}\,\alpha \, = \frac{{377}}{{144}}\).
Câu 16: Rút gọn biểu thức
\(B = \cos \left( {\frac{{3\pi }}{2} – a} \right) + \sin \left( {\frac{{3\pi }}{2} – a} \right) – \cos \left( {\frac{{3\pi }}{2} – a} \right) – \sin \left( {\frac{{3\pi }}{2} + a} \right)\)
A. \( – 2\sin a\);
B. \( – 2\cos a\);
C. \(2\sin a\);
D. \(2\cos a\).
Câu 17: Cho tam giác \(ABC\) có \(\widehat A = 30^\circ \), \(\widehat B = 120^\circ \), AC = 8. Độ dài cạnh AB bằng:
A. \(8\sqrt 3 \);
B. \(\frac{4}{{\sqrt 3 }}\);
C. \(\frac{{8\sqrt 3 }}{3}\);
D. 16.
Câu 18: Góc có số đo 105° đổi sang radian là :
A. \(\frac{{3\pi }}{5}\);
B. \[\frac{{5\pi }}{{12}}\];
C. \[\frac{{7\pi }}{{12}}\];
D. \(\frac{\pi }{4}\) .
Câu 19: Cho tam giác ABC có \(\widehat B = 60^\circ \), AC = 5 và AB = 7. Diện tích của tam giác ABC là:
A. \[\frac{{35}}{2}\] ;
B. \[\frac{{35}}{4}\] ;
C. \[\frac{{35\sqrt 3 }}{4}\] ;
D. \[\frac{{35\sqrt 3 }}{2}\].
Câu 20: Phương trình đường tròn có tâm \[I\left( { – 1;3} \right)\] và bán kính R = 2 là:
A. \({\left( {x + 1} \right)^2} + {\left( {y – 3} \right)^2} = 4\);
B. \({\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\);
C. \({\left( {x – 1} \right)^2} + {\left( {y + 3} \right)^2} = 4\);
D. \({\left( {x + 1} \right)^2} + {\left( {y – 3} \right)^2} = 2\).
B. Phần tự luận
Bài 1. Giải các bất phương trình sau:
a) \(\left( {x + 1} \right)\left( {{x^2} + 6x – 7} \right) \ge 0.\)
b) \(\sqrt {x + 2} + \sqrt {{x^2} – 3} > 3.\)
Bài 2. Biểu diễn miền nghiệm của bất phương trình sau: \(2x + y – 2 \le 0.\)
Bài 3. a) Biết \[\cos a = \frac{2}{3}\] với \( – \frac{\pi }{2} < \alpha < 0\). Tính \[\tan a = ?\]
b) Chứng minh rằng \[\frac{{1 + \sin 2x}}{{1 – \sin 2x}} = {\cot ^2}\left( {x – \frac{\pi }{4}} \right).\]
Bài 4.
a) Viết phương trình tổng quát đường thẳng đi qua 2 điểm \[A\left( {0;2} \right),B\left( {3;0} \right).\]
b) Viết phương trình đường tròn tâm A(–1; 2) và tiếp xúc với đường thẳng \[d:\,\,3x + 4y + 10 = 0.\]
c) Trong mp Oxy cho đường tròn (C): \[{x^2} + {y^2}–2x + 4y = 0\] và điểm A(2; – 4). Tìm tọa độ các đỉnh của hình chữ nhật ABCD nội tiếp trong (C) và có diện tích bằng \[16\sqrt 2 \].
—Hết—
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 2)
I – PHẦN TRẮC NGHIỆM (5,0 điểm): Chọn các khẳng định đúng trong các câu sau
Câu 1. Tập nghiệm của bất phương trình \[(2x – 4)( – {x^2} – 3) \le 0\] là:
A. \[{\rm{[}}2; + \infty )\];
B. \[( – \infty ;2]\];
C. \[{\rm{[3}}; + \infty )\];
D. \[( – \infty ;3]\].
Câu 2. Tìm tất cả các giá trị của tham số m để bất phương trình \[m{x^2} – 6x + m > 0\] nghiệm đúng với \[\forall x \in \mathbb{R}\]
A. m > 3;
B. m < – 3;
C. – 3 < m < 3;
D. \[m \ne \pm 3\].
Câu 3. Trong mặt phẳng tọa độ Oxy, cho Elip\[(E):\frac{{{x^2}}}{{169}} + \frac{{{y^2}}}{{144}} = 1\]. Trục lớn của (E) có độ dài bằng:
A. 12;
B. 13;
C. 26;
D. 24.
Câu 4. Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có tâm I(2; 1), bán kính R = 2 và điểm M(1; 0). Viết phương trình đường thẳng D đi qua điểm M sao cho D cắt (C) tại hai điểm A và B, đồng thời DIAB có diện tích bằng 2.
A. x + 2y – 1 = 0;
B. x – 2y – 1 = 0;
C. x – y – 1 = 0;
D. x + y – 1 = 0.
Câu 5. Trong các phép biển đổi sau, phép biến đổi nào đúng?
A. \[\cos x + \cos 3x = 2\cos 4x\cos 2x\];
B. \[\cos x – \cos 3x = 2\cos 4x\cos 2x\];
C. \[\sin x + \sin 3x = 2\sin 4x\cos 2x\];
D. \[\sin x – \sin 3x = – 2\sin x\cos 2x\].
Câu 6. Biết \[ – \frac{\pi }{2}\, < x < 0,\,\,{\rm{cos}}x\, = \frac{2}{{\sqrt 5 }}\] . Tính giá trị của sin x
A. \[\sin x\, = – \frac{1}{5}\];
B. \[\sin x\, = \frac{1}{5}\];
C. \[\sin x\, = – \frac{{\sqrt 5 }}{5}\];
D. \[\sin x\, = \frac{{\sqrt 5 }}{5}\].
Câu 7. Tập nghiệm của bất phương trình: \({x^2}\left( {{x^2} + 4x + 5} \right) \ge 0\) là:
A. \(\left( { – 1; + \infty } \right);\)
B. \(\mathbb{R};\)
C. \(\emptyset ;\)
D. \(\mathbb{R}\backslash \left\{ 0 \right\}.\)
Câu 8. Cho tan x = – 2. Tính giá trị của biểu thức \(A = \frac{{2\sin x + \cos x}}{{\sin x + \cos x}}\) ?
A. 3;
B. – 4;
C. 4;
D. – 3.
Câu 9. Tính khoảng cách từ điểm \(M( – 2;2)\) đến đường thẳng \(\Delta :5x – 12y – 10 = 0?\)
A. \(\frac{{44}}{{169}};\)
B. \( – \frac{{44}}{{169}};\)
C. \( – \frac{{44}}{{13}};\)\[\]
D. \(\frac{{44}}{{13}}.\)
Câu 10. Trong mặt phẳng tọa độ Oxy, elip (E) đi qua điểm \[M(2\sqrt 6 ;\frac{{\sqrt 5 }}{5})\] và \[N(\sqrt 5 ;2)\]có phương trình chính tắc là:
A. \[\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\];
B. \[\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\];
C. \[\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{5} = 0\];
D. \[\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{5} = 1\].
Câu 11. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn \[(C):{x^2} + {y^2} – 4x – 2y = 0\]và đường thẳng d: x + 2y + 1 = 0. Tìm mệnh đề đúng ?
A. (C) không có điểm chung với d;
B. (C) tiếp xúc d;
C. d đi qua tâm của (C);
D. (C) cắt d tại hai điểm phân biệt.
Câu 12. Số nghiệm của phương trình \[\left| {x – 2} \right| + 4x = {x^2} + 4\] là:
A. 0;
B. 1;
C. 2;
D. 3.
Câu 13. Tập nghiệm của bất phương trình \[{x^2} – x – 2 < 0\] là:
A. (– 1; 2);
B.\(\emptyset \);
C. \(\mathbb{R}\);
D. \[( – \infty ; – 1) \cup (2; + \infty )\].
Câu 14. Biết rằng phương trình \[x + \sqrt {2x + 11} = 0\] có nghiệm là \[x = a + b\sqrt 3 \]. Tìm tích ab
A. – 1;
B. 1;
C. – 2;
D. 2.
Câu 15. Trong mặt phẳng tọa độ Oxy, đường tròn (C) đi qua 3 điểm \[M(2; – 2)\], \[N(3; – 1)\] và \[P( – 1; – 3)\] có tâm là:
A. \[I(1; – 2)\];
B. \[I( – 2;1)\];
C. \[I(2; – 1)\];
D. \[I( – 1;2)\].
Câu 16. Trong mặt phẳng tọa độ Oxy, đường tròn \[(C):{x^2} + {y^2} + 8y – 9 = 0\] có:
A. Tâm \[I(0;4)\], bán kính R = 25;
B. Tâm \[I(0; – 4)\], bán kính R = 3;
C. Tâm \[I( – 4;0)\], bán kính R = 25;
D. Tâm \[I(0; – 4)\], bán kính R = 5.
Câu 17. Biết \[\sin \left( {\frac{x}{2} + \frac{\pi }{4}} \right){\rm{ = }}\sqrt 2 {\rm{cos}}\left( {\frac{x}{2} + \frac{\pi }{4}} \right)\] . Tính giá trị của biểu thức \[P = \frac{{1 + \sin x\,}}{{1 – \sin x}}\]
A. P = 4;
B. P = 3;
C. P = 2;
D. P = 1.
Câu 18. Tìm tất cả các giá trị của tham số m để phương trình \[2{x^2} – (2m – 1)x + 2m – 3 = 0\] có hai nghiệm x phân biệt.
A. \[m = \frac{5}{2}\];
B. \[m > \frac{5}{2}\];
C. \[m \ne \frac{5}{2}\];
D. \[m < \frac{5}{2}\].
Câu 19. DABC có các góc A, B, C thỏa mãn \[5 – \cos 2A – \cos 2B – \cos 2C = 4(\sin A.\sin B + \sin C)\] là:
A. Tam giác đều;
B. Tam giác vuông nhưng không cân;
C. Tam giác vuông cân;
D. Tam giác cân nhưng không vuông.
Câu 20. Trong mặt phẳng tọa độ Oxy, đường thẳng \[\left\{ \begin{array}{l}x = 2 – 3t\\y = – 3 + 2t\end{array} \right.\begin{array}{*{20}{c}}{}\end{array}(t \in R)\] có một véctơ chỉ phương là:
A. \[\overrightarrow u \, = (2; – 3)\];
B. \[\overrightarrow u \, = (6;4)\];
C. \[\overrightarrow u \, = (6; – 4)\];
D. \[\overrightarrow u \, = (2;3)\].
II – PHẦN TỰ LUẬN (5,0 điểm)
Bài 1. a) Giải bất phương trình sau: \(\frac{{2{x^2} – 3x – 2}}{{2x + 3}} \ge 0\).
b) Giải bất phương trình sau: \(\sqrt {{x^2} – x – 6} \le x – 1\).
Bài 2. Chứng minh rằng: \[4\sin x{\rm{.}}\sin \left( {\frac{\pi }{3} + x} \right){\rm{.}}\sin \left( {\frac{\pi }{3} – x} \right){\rm{ = }}\sin 3x\] với \[\forall x \in \mathbb{R}\].
Bài 3. Trong mặt phẳng tọa độ Oxy, cho điểm \[M( – 1;2)\]. Viết phương trình đường tròn (C) đi qua điểm M đồng thời tiếp xúc với hai trục tọa độ Ox và Oy.
Bài 4. Trong mặt phẳng tọa độ Oxy, đường tròn \[(C):{x^2} + {y^2} + 4x – 2y – 1 = 0\] và đường thẳng \[(\Delta ):3x – 4y + 2017 = 0\]. Viết phương trình tiếp tuyến của (C), biết rằng tiếp tuyến đó song song với đường thẳng ∆.
—Hết—
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 3)
I. Phần trắc nghiệm: (5 điểm)
Câu 1: Tìm tập xác định D của hàm số \(f\left( x \right) = \frac{{{x^2} – x}}{{\sqrt {2x + 6} }} – \sqrt {10 – x} .\)
A. \(D = \left( { – 3;10} \right];\)
B. \(D = \left[ { – 3;10} \right];\)
C. \(D = \left( { – 3;10} \right);\)
D. \(D = \left[ { – 3;10} \right).\)
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình \({x^2} – 2mx + {m^2} – 1 = 0\) có hai nghiệm dương phân biệt?
A. \(m \in \left[ {1; + \infty } \right);\)
B. \(m \in \left( {1; + \infty } \right);\)
C. \(m \in \left( { – \infty ; – 1} \right) \cup \left( {1; + \infty } \right);\)
D. \(m \in \left( { – \infty ; + \infty } \right).\)
Câu 3: Thống kê điểm kiểm tra môn toán (thang điểm 10) của một nhóm gồm 6 học sinh ta có bảng số liệu sau:
|
Tên học sinh |
Kim |
Sơn |
Ninh |
Bình |
Việt |
Nam |
|
Điểm |
9 |
8 |
7 |
10 |
8 |
9 |
Tìm độ lệch chuẩn \(s\)của bảng số liệu trên (làm tròn đến hàng phần trăm).
A. s = 0,92;
B. s = 0,95;
C. s = 0,96;
D. s = 0,91.
Câu 4: Cho cung x thỏa mãn điều kiện tồn tại của các biểu thức. Mệnh đề nào sau đây sai?
A. \(\sin 2x = 2\tan x.{\cos ^2}x;\)
B. \(\cos 2x = {\cos ^4}x – {\sin ^4}x;\)
C. \(\tan 2x = 2{\tan ^2}x – 1;\)
D. \({\sin ^2}2x + {\cos ^2}2x = 1.\)
Câu 5: Biểu thức sau không phụ thuộc vào giá trị của cung x. Tính giá trị biểu thức T.
\(T = 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right) – 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) + 5.\)
A. T = – 1;
B. T = 4;
C. T = 6;
D. T = 5.
Câu 6: Trong mặt phẳng toạ độ Oxy, cho đường tròn (S) có phương trình \({x^2} + {y^2} – 2x – 8 = 0.\) Tính chu vi C của đường tròn (S).
A. \(C = 3\pi ;\)
B. \(C = 6\pi ;\)
C. \(C = 2\pi ;\)
D. \(C = 4\sqrt 2 \pi .\)
Câu 7: Trong mặt phẳng toạ độ Oxy, phương trình nào dưới đây là phương trình chính tắc của elip (E) có một tiêu điểm là \({F_2}\left( {3;0} \right)\) và có trục lớn dài hơn trục bé 2 đơn vị.
A. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1;\)
B. \(\frac{{{x^2}}}{{25}} – \frac{{{y^2}}}{9} = 1;\)
C. \(\frac{{{x^2}}}{{25}} – \frac{{{y^2}}}{{16}} = 1;\)
D. \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1.\)
Câu 8: Trong mặt phẳng toạ độ Oxy, cho điểm \(M\left( {1;3} \right).\) Tìm phương trình đường thẳng (d) đi qua M cắt các tia Ox, Oy lần lượt tại \(A\) và \(B\) sao cho diện tích tam giác \(OAB\) nhỏ nhất.
A. \(\frac{x}{3} + \frac{{2y}}{9} = 1;\)
B. \(\frac{x}{2} + \frac{y}{6} = 1;\)
C. \(\frac{{2x}}{3} + \frac{y}{9} = 1;\)
D. \(\frac{x}{4} + \frac{y}{4} = 1.\)
Câu 9: Biểu thức thu gọn của biểu thức \(B = \left( {\frac{1}{{{\rm{cos}}2{\rm{x}}}} + 1} \right).\tan x\) là:
A. \(\tan 2{\rm{x}}\);
B. \(\cot 2{\rm{x}}\) ;
C. \({\rm{cos2x}}\) ;
D. \(\sin {\rm{x}}\).
Câu 10: Cho tam giác ABC, chọn công thức đúng trong các đáp án sau:
A. \[m_a^2 = \frac{{{b^2} + {c^2}}}{2} + \frac{{{a^2}}}{4};\]
B. \[m_a^2 = \frac{{{a^2} + {c^2}}}{2} – \frac{{{b^2}}}{4};\]
C. \[m_a^2 = \frac{{{a^2} + {b^2}}}{2} – \frac{{{c^2}}}{4};\]
D. \[m_a^2 = \frac{{2{c^2} + 2{b^2} – {a^2}}}{4}.\]
Câu 11: Cho tam giác ABC, chọn công thức đúng ?
A. \(A{B^2} = A{C^2} + B{C^2} – 2AC.AB\cos C\);
B. \(A{B^2} = A{C^2} – B{C^2} + 2AC.BC\cos C\);
C. \(A{B^2} = A{C^2} + B{C^2} – 2AC.BC\cos C\);
D. \(A{B^2} = A{C^2} + B{C^2} – 2AC.BC + \cos C\).
Câu 12: Cho tam giác ABC, biết a = 13; b = 14; c = 15. Tính góc \(B\) ?
A. \({59^0}49′;\)
B. \({53^0}7′;\)
C. \({59^0}29’\,;\)
D. \({62^0}22′.\)
Câu 13: Tam giác ABC có a = 16,8; \(\widehat B = {56^0}13’\); \(\widehat C = {71^0}\). Cạnh c bằng bao nhiêu?
A. 29,9;
B. 14,1;
C. 17,5;
D. 19,9.
Câu 14: Cho tam giác ABC có a = 4, b = 6, c = 8. Khi đó diện tích của tam giác là:
A. \(9\sqrt {15} ;\)
B. \(3\sqrt {15} ;\)
C. \(105;\)
D. \(\frac{2}{3}\sqrt {15} .\)
Câu 15: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc \({56^0}16’\). Biết \(CA = 200\,m\), \(CB = 180\,m\). Khoảng cách AB bằng bao nhiêu ?
A. 163 m;
B. 224 m;
C. 112 m;
D. 180 m.
Câu 16: Cho đường thẳng (d): \(2x + 3y – 4 = 0\) . Vec tơ nào sau đây là vectơ pháp tuyến của (d)?
A. \(\overrightarrow {{n_1}} = \left( {3;2} \right)\) ;
B. \(\overrightarrow {{n_2}} = \left( { – 4; – 6} \right)\);
C. \(\overrightarrow {{n_3}} = \left( {2; – 3} \right)\);
D. \(\overrightarrow {{n_4}} = \left( { – 2;3} \right)\).
Câu 17: Cho đường thẳng \(\left( d \right):\left\{ \begin{array}{l}x = 2 – 3t\\y = – 1 + 2t\end{array} \right.\)và điểm \(A\left( {\frac{7}{2}; – 2} \right).\) Điểm \(A \in \left( d \right)\) ứng với giá trị nào của t?
A. \(t = \frac{3}{2};\)
B. \(t = \frac{1}{2};\)
C. \(t = – \frac{1}{2};\)
D. t = 2.
Câu 18: Khoảng cách từ điểm M(0; 1) đến đường thẳng ∆: \(5x – 12y – 1 = 0\) là :
A.\(\frac{{11}}{{13}}\);
B. \(\sqrt {13} \);
C. 1;
D. \(\frac{{13}}{{17}}\).
Câu 19: Tìm tọa độ giao điểm của 2 đường thẳng D: 4x – 3y – 26 = 0 và đường thẳng d: 3x + 4y – 7 = 0.
A. (2 ; -6);
B. (5 ; 2);
C. (5 ; -2);
D. Không có giao điểm.
Câu 20: Cho phương trình \({x^2} + {y^2} – 2ax – 2by + c = 0{\rm{ }}(1)\) . Điều kiện để (1) là phương trình của đường tròn là:
A.\({a^2} + {b^2} – 4c > 0\);
B.\({a^2} + {b^2} – c > 0\);
C.\({a^2} + {b^2} – 4c \ge 0\);
D.\({a^2} + {b^2} – c \ge 0\).
II. Phần tự luận: (5 điểm)
Bài 1: Giải bất phương trình \(\frac{{{x^2} – 3x}}{{2 – x}} \le 0.\)
Bài 2: Giải phương trình \(\sqrt {{x^2} + 2x – 3} = 2 – x.\)
Bài 3:
a) Tìm tất cả các giá trị thực của \(m\) để \(m{x^2} – mx + 1 > 0\) với mọi \(x \in \mathbb{R}.\)
b) Cho \(\pi < \alpha < \frac{{3\pi }}{2}\) và \(\sin \alpha = – \frac{1}{3}.\) Tính \(\cos \alpha \) và \(cos2\alpha .\)
Bài 4: Trong mặt phẳng tọa độ Oxy, cho điểm \(A\left( { – 1;2} \right)\) và đường thẳng \(\left( \Delta \right):3x – 4y – 2 = 0.\) Tính khoảng cách từ A tới \(\left( \Delta \right)\), viết phương trình đường thẳng \(\left( d \right)\) qua A và song song với \(\left( \Delta \right).\)
—Hết—
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 4)
I. TRẮC NGHIỆM (5 điểm):
Câu 1: Biểu thức: \(A = \cot \left( {\frac{\pi }{2} – x} \right).\cot \left( {\pi + x} \right)\) được rút gọn bằng:
A. – 1;
B. 1;
C. tan x;
D. cot x.
Câu 2: Cho tam giác ABC có \[b = 7,\,\,\widehat B = {30^0}\]. Khi đó bán kính đường tròn ngoại tiếp của tam giác ABC là:
A. \(\frac{7}{{\sqrt 3 }};\)
B. \(\frac{7}{2};\)
C. 14;
D. 7.
Câu 3: Cho \(\cot x = \sqrt 2 \). Tính giá trị của biểu thức \(A = \frac{{{{\sin }^2}x + \sin x\cos x + 1}}{{{{\sin }^2}x\, – {{\cos }^2}x}}\) ?
A. \(4 + \sqrt 2 ;\)
B. \( – 4 – \sqrt 2 ;\)
C. \( – 4 + \sqrt 2 ;\)
D. \(4 – \sqrt 2 .\)
Câu 4: Tập nghiệm của bất phương trình: \({x^2}\left( {{x^2} + 4x + 5} \right) \ge 0\) là:
A. \(\left( { – 1; + \infty } \right);\)
B. \(\mathbb{R};\)
C. \(\emptyset ;\)
D. \(\mathbb{R}\backslash \left\{ 0 \right\}.\)
Câu 5: Phương trình – 2mx + 6 = 0 vô nghiệm khi:
A. m = 2;
B. m = – 2;
C. m = 0;
D. m ≠ 0.
Câu 6: Phương trình \({x^2} + 2mx + {m^2} – m + 6 = 0\) vô nghiệm khi:
A. m > 4;
B. m < 4;
C. m < 6;
D. m > 6.
Câu 7: Giá trị nhỏ nhất của hàm số\(y = x + \frac{9}{x}\) \[\left( {x > 0} \right)\] là:
A. – 6;
B. 9;
C. 0;
D. 6.
Câu 8: Cho a > 0 khi đó \(a + \frac{4}{a} \ge 4.\) Dấu đẳng thức xảy ra khi
A. a = 2;
B. a = ± 2;
C. a = 4;
D. a = – 2.
Câu 9: Cho tan x = – 2. Tính giá trị của biểu thức \(A = \frac{{2\sin x + \cos x}}{{\sin x + \cos x}}\) ?
A. 3;
B. – 4;
C. 4;
D. – 3.
Câu 10: Cho đường thẳng \(d:7{\rm{x}} – 2y + 10 = 0\). Vectơ chỉ phương của đường thẳng d là:
A. \(\overrightarrow u = (7; – 2);\)
B. \(\overrightarrow u = ( – 2;7);\)
C. \(\overrightarrow u = (7;2);\)
D. \(\overrightarrow u = (2;7).\)
Câu 11: Phương trình tham số của đường thẳng d đi qua M(– 2; 3) và có 1 vectơ chỉ phương \(\overrightarrow u = (1; – 4)\) là:
A. \(\left\{ \begin{array}{l}x = – 2 + t\\y = 3 – 4t\end{array} \right.(t \in \mathbb{R})\);
B. \(\left\{ \begin{array}{l}x = 1 – 4t\\y = – 2 + 3t\end{array} \right.(t \in \mathbb{R});\)
C. \(\left\{ \begin{array}{l}x = – 2 + 3t\\y = 1 – 4t\end{array} \right.(t \in \mathbb{R});\)
D. \(\left\{ \begin{array}{l}x = 1 – 2t\\y = – 4 + 3t\end{array} \right.(t \in \mathbb{R}).\)
Câu 12: Một đường thẳng có phương trình tham số\(:\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.,t \in \mathbb{R}.\)
Khi đó, một vectơ pháp tuyến của đường thẳng:
A. (a; b);
B. (– a; – b);
C. (– b; a);
D. (– b; – a).
Câu 13: Tính khoảng cách từ điểm \(M( – 2;2)\) đến đường thẳng \(\Delta :5x – 12y – 10 = 0?\)
A. \(\frac{{44}}{{169}};\)
B. \( – \frac{{44}}{{169}};\)
C. \( – \frac{{44}}{{13}};\)\[\]
D. \(\frac{{44}}{{13}}.\)
Câu 14: Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn \[(C):{x^2} + {y^2} – 4x – 2y = 0\]và đường thẳng d: x + 2y + 1 = 0. Tìm mệnh đề đúng ?
A. (C) không có điểm chung với d;
B. (C) tiếp xúc d;
C. d đi qua tâm của (C);
D. (C) cắt d tại hai điểm phân biệt.
Câu 15: Đường tròn (C) có tâm \(I\left( {3; – 2} \right)\)và tiếp xúc với đường thẳng \(\Delta 😡 – y – 1 = 0\) có bán kính bằng:
A. \(R = \frac{1}{{\sqrt 2 }};\)
B. \(R = 2\sqrt 2 ;\)
C. R = 4;
D. R = 2.
Câu 16: Cho tam giác ABC có \[b = 4\,cm\,,\,\,c = 5\,cm\,,\,\,\widehat {\hat A} = {60^0}\]. Khi đó diện tích của tam giác ABC là:
A. 5;
B. 10;
C. \(5\sqrt 3 ;\)
D. \(10\sqrt 3 .\)
Câu 17: Cho hai điểm \(A\left( {1;1} \right)\)và \(B\left( {7;5} \right).\) Đường tròn đường kính AB có tâm là:
A. \(I\left( {4;3} \right);\)
B. \(I\left( { – 4;3} \right);\)
C. \(I\left( {3;4} \right);\)
D. \(I\left( {6;4} \right).\)
Câu 18: Tập nghiệm của bất phương trình: \[\frac{{\left( {x + 1} \right)\left( { – x + 1} \right)}}{{2x – 6}} \le 0\] là:
A. \[\left[ { – 1;1} \right] \cup \left( {3; + \infty } \right);\]
B. \(\left( { – 1;1} \right) \cup \left( {3; + \infty } \right);\)
C. \(\left( { – \infty ; – 1} \right] \cup \left( {1;3} \right);\)
D. \[\left[ { – 1;1} \right] \cup \left[ {3; + \infty } \right).\]
Câu 19: Trong mặt phẳng với hệ tọa độ Oxy, phương trình tiếp tuyến tại điểm M(3; 4) với đường tròn \[(C):{x^2} + {y^2} – 2x – 4y – 3 = 0.\]
A. x + y + 7 = 0;
B. x – y – 7 = 0;
C. x + y – 7 = 0;
D. x + y – 3 = 0.
Câu 20: Biểu thức:
\(B = \tan \left( {2017\pi + x} \right) + \tan \left( {2018\pi – x} \right) + 2\cos \left( {\frac{\pi }{2} – x} \right) – sin\left( {\pi – x} \right)\)
được rút gọn bằng:
A. – cos x;
B. cos x;
C. – sin x;
D. sin x.
II. TỰ LUẬN (5 điểm):
Bài 1: Giải bất phương trình sau: \[\left( {x + 3} \right)\left( { – 2{x^2} + 3x – 1} \right) < 0\].
Bài 2:
a) Cho \[\sin \alpha = \frac{{12}}{{13}}\,\] với \[0 < \alpha < \frac{\pi }{2}.\] Tính các giá trị lượng giác còn lại của cung α.
b) Chứng minh đẳng thức lượng giác sau: \(\frac{{1 + \sin x}}{{\cos x}} = \frac{{\cos x}}{{1 – \sin x}}.\)
Bài 3: Viết phương trình đường tròn (C) có tâm \(I\left( { – 4; – 4} \right)\) và đi qua \(M\left( { – 8;0} \right).\)
Bài 4: Trong mp Oxy, cho tam giác ABC vuông tại B, AB = 2 BC. Gọi D là trung điểm AB, E nằm trên đoạn AC sao cho AC = 3 EC. Phương trình đường thẳng \(CD:x – 3y + 1 = 0;\,BE:3x + y – 17 = 0\) và \(E\left( {\frac{{16}}{3};1} \right).\)Tìm tọa độ điểm B.
–––Hết–––
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 5
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 5)
I. PHẦN TRẮC NGHIỆM (5,0 điểm)
Câu 1: Biểu thức f(x) = 3x + 5 nhận giá trị dương khi và chỉ khi:
A. \[x > – \frac{5}{3};\]
B. \[x \ge – \frac{5}{3};\]
C. \[x < – \frac{5}{3};\]
D. \[x > \frac{5}{3}.\]
Câu 2: Tập nghiệm của bất phương trình \(\frac{{2x – 3}}{3} > \frac{{x – 1}}{2}\) là
A. \(\left( {3; + \infty } \right)\);
B. \(\left( { – 3; + \infty } \right)\);
C. \(\left( {2; + \infty } \right)\);
D. \(\left( { – 2; + \infty } \right)\).
Câu 3: Cho hệ bất phương trình \[\left\{ \begin{array}{l}x + 2y – 3 < 0\\2x + y – 2 > 0\end{array} \right.\]. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
A. \[P\left( {3; – 1} \right)\];
B. \[N\left( {2;2} \right)\];
C. \[M\left( {2;3} \right)\];
D. \[Q\left( { – 1; – 5} \right)\].
Câu 4: Cho biểu thức \[f\left( x \right) = a{x^2} + bx + c(a \ne 0)\] và \[\Delta = {b^2} – 4ac\]. Chọn khẳng định đúng?
A. Khi \[\Delta < 0\] thì \[f\left( x \right)\] cùng dấu với hệ số a với mọi \[x \in \mathbb{R}\];
B. Khi \[\Delta = 0\] thì \[f\left( x \right)\] trái dấu với hệ số a với mọi \[x \ne – \frac{b}{{2a}}\];
C. Khi \[\Delta < 0\] thì \[f\left( x \right)\] cùng dấu với hệ số a với mọi \[x \ne – \frac{b}{{2a}}\];
D. Khi \[\Delta > 0\] thì \[f\left( x \right)\] luôn trái dấu hệ số a với mọi \[x \in \mathbb{R}\].
Câu 5: Tìm tập nghiệm của bất phương trình \[ – {x^2} + 2016x + 2017 > 0\].
A. \(\left( { – 1;2017} \right);\)
B. \(\left( { – \infty ; – 1} \right) \cup \left( {2017; + \infty } \right);\)
C. \(\left( { – \infty ; – 1} \right] \cup \left[ {2017; + \infty } \right);\)
D. \(\left[ { – 1;2017} \right].\)
Câu 6: Tìm tất cả các giá trị của tham số m đề bất phương trình \[{x^2} + \left( {2m + 1} \right)x + {m^2} + 2m – 1 > 0\] nghiệm đúng với mọi x
A. \[m > \frac{5}{4}\];
B. \[m < \frac{5}{4}\];
C. \[m < – \frac{5}{4}\];
D. \[m > – \frac{5}{4}\].
Câu 7: Cho \[0 < \alpha < \frac{\pi }{2}\]. Hãy chọn khẳng định đúng?
A. \[\sin \alpha > 0\];
B. \[\sin \alpha < 0\];
C. \[\cos \alpha < 0\];
D. \[\tan \alpha < 0\].
Câu 8: Kết quả điểm kiểm tra môn Toán của 40 học sinh lớp 10A được trình bày ở bảng sau
|
Điểm |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Tần số |
2 |
8 |
7 |
10 |
8 |
3 |
2 |
40 |
Tính số trung bình cộng của bảng trên. (làm tròn kết quả đến một chữ số thập phân).
A. 6,8;
B. 6,4;
C. 7,0;
D. 6,7.
Câu 9: Chọn khẳng định đúng ?
A. \[1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\];
B. \[{\sin ^2}x – {\cos ^2}x = 1\];
C. \[\tan x = – \frac{1}{{\cot x}}\];
D. \[\sin x + \cos x = 1\].
Câu 10: Chọn khẳng định đúng?
A. \[\cos \left( {\pi – \alpha } \right) = – \cos \alpha \];
B. \[\cot \left( {\pi – \alpha } \right) = \cot \alpha \];
C. \[\tan \left( {\pi – \alpha } \right) = \tan \alpha \];
D. \[\sin \left( {\pi – \alpha } \right) = – \sin \alpha \].
Câu 11: Tính giá trị của biểu thức \[P = \frac{{2\sin \alpha – 3\cos \alpha }}{{4\sin \alpha + 5\cos \alpha }}\] biết \[\cot \alpha = – 3\].
A. – 1;
B. \[\frac{7}{9}\];
C. \[\frac{9}{7}\];
D. 1.
Câu 12: Với mọi a. Khẳng định nào dưới đây sai?
A. \[\sin acosa = 2\sin 2a\];
B. \[2co{s^2}a = cos2a + 1\];
C. \[2si{n^2}a = 1 – cos2a\];
D. \[co{s^2}a – si{n^2}a = cos2a\].
Câu 13: Với mọi a, b. Khẳng định nào dưới đây đúng?
A. \[sin(a + b) = sina.cosb + sinb.cosa\];
B. \[cos(a + b) = cosa.\sin b – sina.\cos b\];
C. \[cos(a + b) = cosa.cosb + sina.sinb\];
D. \[sin(a + b) = sina.sinb + cosa.cosb\].
Câu 14: Tìm một vectơ chỉ phương của đường thẳng \[d:\left\{ \begin{array}{l}x = – 1 + 2t\\y = 3 – 5t\end{array} \right.\]
A.\[\overrightarrow u = (2; – 5)\];
B. \[\overrightarrow u = (5;2)\];
C. \[\overrightarrow u = ( – 1;3)\];
D. \[\overrightarrow u = ( – 3;1)\].
Câu 15. Trong mặt phẳng Oxy cho hai điểm \[A\left( {1; – 3} \right),B\left( { – 2;5} \right)\]. Viết phương trình tổng quát đi qua hai điểm A, B
A. \[8x + 3y + 1 = 0\];
B. \[8x + 3y – 1 = 0\];
C. \[ – 3x + 8y – 30 = 0\];
D. \[ – 3x + 8y + 30 = 0\].
Câu 16: Trong mặt phẳng Oxy cho \[\left( C \right):{\left( {x – 3} \right)^2} + {\left( {y + 2} \right)^2} = 9\]. Tọa độ tâm I và bán kính R của đường tròn (C) là
A. \[I\left( {3; – 2} \right),R = 3\];
B. \[I\left( {2; – 3} \right),R = 3\];
C. \[I\left( { – 2;3} \right),R = 3\];
D. \[I\left( { – 3;2} \right),R = 3\].
Câu 17: Trong mặt phẳng Oxy cho hai điểm M(2; 5) và N(5; 1). Phương trình đường thẳng đi qua M và cách N một đoạn có độ dài bằng 3 là
A. \(x – 2 = 0\)hoặc \(7x + 24y – 134 = 0\);
B. \(y – 2 = 0\)hoặc \(24x + 7y – 134 = 0\);
C. \(x + 2 = 0\)hoặc \(7x + 24y + 134 = 0\);
D. \(y + 2 = 0\)hoặc \(24x + 7y + 134 = 0\).
Câu 18: Bán kính của đường tròn tâm \[I( – 2; – 1)\]và tiếp xúc với đường thẳng \(4x – 3y + 10 = 0\) là
A. R = 1;
B.\[R = \frac{1}{5}\];
C. R =\(3\);
D. \[R = \sqrt 5 \].
Câu 19. Trong mặt phẳng Oxy cho \[\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\]. Tọa độ hai tiêu điểm của Elip là
A. \[{F_1}\left( { – 4;0} \right),{F_2}\left( {4;0} \right)\];
B. \[{F_1}\left( {0; – 4} \right),{F_2}\left( {0;4} \right)\];
C. \[{F_1}\left( {0; – 8} \right),{F_2}\left( {0;8} \right)\];
D. \[{F_1}\left( { – 8;0} \right),{F_2}\left( {8;0} \right)\].
Câu 20: Trong mặt phẳng Oxy cho \[\left( C \right):{\left( {x – 2} \right)^2} + {\left( {y + 1} \right)^2} = 4\]. Viết phương trình tiếp tuyến của đường tròn (C), biết tiếp tuyến song song với \[d:4x – 3y + 5 = 0\].
A. \[4x – 3y – 1 = 0\] hoặc \[4x – 3y – 21 = 0\];
B. \[4x – 3y + 1 = 0\] hoặc \[4x – 3y + 21 = 0\];
C. \[3x + 4y – 1 = 0\] hoặc \[3x + 4y – 21 = 0\];
D. \[3x + 4y + 1 = 0\] hoặc \[3x + 4y + 21 = 0\].
II. PHẦN TỰ LUẬN (5,0 điểm)
Bài 1: (1,5 điểm) Giải bất phương trình sau: \[\frac{{\left( { – x + 3} \right)\left( {{x^2} + 3x – 4} \right)}}{{ – {x^2} + 4x – 4}} > 0\].
Bài 2: (2,0 điểm)
a. Chứng minh rằng: \(\frac{{{{(\sin x + \cos x)}^2} – 1}}{{\cot x – \sin x\cos x}} = 2{\tan ^2}x\).
b. Cho \(\cos \alpha = – \frac{1}{4},\,\,\,\,\frac{\pi }{2} < \alpha < \pi \). Tính \(\sin 2\alpha ,\cos 2\alpha \).
Bài 3: (1,0 điểm) Trong mặt phẳng Oxy, cho tam giác ABC biết A(3; 7), B(1; 1), C(– 5; 1). Tìm tọa độ trung điểm M của đoạn thẳng BC. Viết phương trình đường trung tuyến AM.
Bài 4: (0,5 điểm) Trong mặt phẳng Oxy, cho M(– 1; 1), N(1; – 3). Viết phương trình đường tròn đi qua hai điểm M, N và có tâm nằm trên đường thẳng d: 2x – y + 1 = 0.
–––Hết–––
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 6
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 6)
A. TRẮC NGHIỆM (5 điểm).
Câu 1. Tìm m để phương trình \({x^2} + 2\left( {m + 1} \right)x + {m^2} – 1 = 0\)có hai nghiệm trái dấu ?
A.\( – 1 < m \vee m > 1\);
B.\(m > – 1\);
C.\(m < 1\);
D.\( – 1 < m < 1\).
Câu 2. Tập nghiệm của bất phương trình \(\frac{{4 – 3{x^2}}}{{{x^2} + x}} \le – 3\) là:
A.\(T = ( – \infty ; – \frac{4}{3}{\rm{]}} \cup {\rm{[}} – 1;0]\);
B.\(T = ( – \frac{4}{3}; – 1) \cup (0; + \infty )\);
C.\(T = ( – \frac{4}{3}; – 1{\rm{]}} \cup (0; + \infty )\);
D. \(T = ( – \infty ; – \frac{4}{3}{\rm{]}} \cup ( – 1;0)\).
Câu 3. Phương trình tham số của đường thẳng đi qua hai điểm A(2; 3) và B(3; 1) là:
A.\(\left\{ {\begin{array}{*{20}{c}}{x = 2 – 2t}\\{y = 3 + t}\end{array}} \right.\);
B.\(\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y = 3 – 2t}\end{array}} \right.\);
C.\(\left\{ {\begin{array}{*{20}{c}}{x = 2 – t}\\{y = 3 – 2t}\end{array}} \right.\);
D.\(\left\{ {\begin{array}{*{20}{c}}{x = 3 + 2t}\\{y = 1 + t}\end{array}} \right.\).
Câu 4. Tập nghiệm của bất phương trình \(x({x^2} – 1) \ge 0\) là:
A.\[{\rm{[}} – 1;1]\];
B.\[{\rm{[}} – 1;0] \cup \left[ {1; + \infty } \right)\];
C.\(( – \infty ; – 1) \cup {\rm{[}}0;1)\);
D.\[( – \infty ; – 1] \cup (1; + \infty )\].
Câu 5. Đường Elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{6} = 1\) có một tiêu điểm là
A.\(\left( { – \sqrt 3 ;0} \right)\);
B.\(\left( {0;\sqrt 3 } \right)\);
C. (0; 3);
D. (3; 0).
Câu 6. Với giá trị nào của m thì biểu thức \(2{x^2} – (m + 3)x + 2m\) luôn dương?
A.\(1 < m < 9\);
B.\(m \ge 1\);
C.\(m \le 9\);
D.\(m < 1\) hoặc \(m > 9\).
Câu 7. Trong các khẳng định sau, khẳng định nào đúng?
A.\({\cos ^2}\alpha – {\sin ^2}\alpha = 1\);
B.\(\tan (\alpha – \beta ) = \frac{{\tan \alpha + \tan \beta }}{{1 – \tan \alpha \tan \beta }}\);
C.\(\cos (\alpha + \beta ) = \cos \alpha + \cos \beta \);
D.\[\sin \alpha \sin \beta = \frac{1}{2}{\rm{[cos(}}\alpha – \beta {\rm{)}} – {\rm{cos(}}\alpha {\rm{ + }}\beta {\rm{)]}}\].
Câu 8. Giá trị của m để bất phương trình \(\left( {m + 2} \right){x^2} – 2\left( {m – 1} \right)x + 4 < 0\) vô nghiệm là
A.\( – 1 \le m \le 7\);
B.\( – 7 \le m \le 1\);
C.\(m \le – 1\) hoặc \(m \ge 7\);
D.\( – 1 < m < 7\).
Câu 9. Tập nghiệm của bất phương trình \( – 5{x^2} + 4x + 12 < 0\) là:
A. \(\mathbb{R}\);
B.\(( – \infty ; – \frac{6}{5}) \cup (2; + \infty )\);
C.\(( – \frac{6}{5};2)\);
D.\(( – \infty ; – \frac{6}{5})\).
Câu 10. Trong mặt phẳng Oxy, cho đường thẳng ∆:\(4x – 3y + 1 = 0\). Vectơ nào dưới đây không phải là vectơ pháp tuyến của đường thẳng ∆?
A.(–8 ; 6);
B.(8 ; 6);
C.(4 ; –3);
D.(8 ; –6).
Câu 11. Trong các đẳng thức sau đẳng thức nào sai:
A.\(\tan (\frac{\pi }{2} – x) = \cot x\);
B.\(\tan (\frac{\pi }{2} + x) = \cot x\);
C.\(\sin (\frac{\pi }{2} + x) = \cos x\);
D.\(\sin (\frac{\pi }{2} – x) = \cos x\).
Câu 12. Tập nghiệm của phương trình \(\left| {2{x^2} – 5x + 2} \right| = x + 2\) là
A.{ – 3; 3};
B. {– 2; 1};
C. {0; 3};
D. {– 4; 4}.
Câu 13. Giá trị của \(\cot \frac{{89\pi }}{6}\) là:
A.\(\frac{{\sqrt 3 }}{3}\);
B.\(\sqrt 3 \);
C.\( – \frac{{\sqrt 3 }}{3}\);
D.\( – \sqrt 3 \).
Câu 14. Nghiệm của phương trình \(\frac{{{x^2}}}{{x – 1}} = 4 + \frac{1}{{x – 1}}\) là
A.\(x = 3 \vee x = 1\);
B.\(x = 1\);
C.\(x = 3\);
D.\(x = – 3 \vee x = – 1\).
Câu 15. Tìm giá trị của \(c{\rm{os}}(2\alpha )\) biết \(c{\rm{os}}\alpha = – \frac{5}{{13}}\)là
A.\( – \frac{{169}}{{119}}\);
B.\( – \frac{{119}}{{169}}\);
C.\( \pm \frac{{169}}{{119}}\);
D.\( \pm \frac{{119}}{{169}}\).
Câu 16. Tìm giá trị của \(\sin \alpha \) biết \(c{\rm{os}}\alpha = – \frac{3}{5}\)và \(\frac{\pi }{2} < \alpha < \pi \)là
A. \(\frac{4}{5}\);
B. \( – \frac{5}{4}\);
C. \(\frac{5}{4}\);
D. \( – \frac{4}{5}\).
Câu 17. Giá trị x = 0 là nghiệm của bất phương trình nào sau đây?
A.\(\sqrt {5 – x} + x \ge \sqrt {5 – x} + 1\);
B.\(\sqrt {x – 3} < 1 + \sqrt {x – 3} \);
C.\(\sqrt {{x^2} – 4x} \) >\(x – 3\);
D.\(\frac{1}{{x – 1}} \ge 1\).
Câu 18. Góc có số đo 108° đổi sang radian là:
A.\(\frac{{3\pi }}{2}\);
B.\(\frac{{4\pi }}{5}\);
C.\(\frac{{3\pi }}{5}\);
D.\(\frac{\pi }{5}\).
Câu 19. Trong các khẳng định sau khẳng định nào đúng:
A.\(x > 0 \Rightarrow \sin x > 0\);
B.\(0 < x < \pi \Rightarrow \cos x < 0\);
C.\(x > 0 \Rightarrow \cos x > 0\);
D.\(0 < x < \pi \Rightarrow \sin x > 0\).
Câu 20.Tìm góc giữa 2 đường thẳng ∆1 : \(2x – y – 10 = 0\) và ∆2 : \(x – 3y – 9 = 0\)
A. 45°;
B. 0°;
C. 60°;
D. 90°.
B. TỰ LUẬN (5 điểm).
Bài 1. Giải các bất phương trình sau:
a) \(\frac{{ – 2{x^2} + 7x – 3}}{{({x^2} – 3x + 2)(x + 1)}} \le 0\);
b) \(\frac{{{x^2} + 3x + 8}}{{{x^2} + 5x + 6}}\,\, > 1.\)
Bài 2.
a) Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(–1; 2), B(2; –4), C(1; 0). Viết phương trình tổng quát của đường trung tuyến AM của tam giác ABC.
b) Viết phương trình đường tròn (C) biết (C) qua 2 điểm A(1; 4), B(–7; 4) và có tâm nằm trên đường thẳng (d): \(x = – 2\).
Bài 3. Chứng minh rằng :
\(\frac{{4{\mathop{\rm s}\nolimits} {\rm{inx}} + \sin 2x – {\rm{4}}{{\sin }^3}{\rm{x}}}}{{1 + \cos {\rm{x + cos}}2{\rm{x}}}} = 2{\mathop{\rm s}\nolimits} {\rm{inx}}{\rm{.}}\)
Bài 4. Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán.
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Số học sinh |
2 |
3 |
7 |
18 |
3 |
2 |
4 |
1 |
40 |
Hãy tính điểm trung bình của các số liệu thống kê đã cho.
–––Hết–––
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 7
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 7)
I. TRẮC NGHIỆM
Câu 1: Trong các giá trị sau, giá trị nào không là nghiệm của BPT 2x + 1 > 0.
A. x = 1;
B. x = 2;
C. x = \( – \frac{4}{3}\);
D. x = 6.
Câu 2: Điều kiện xác định của bất phương trình \(\frac{1}{{2x – 2}} + \sqrt {x + 3} > x + \sqrt {6 – x} \) là:
A. \(D = \left[ { – 3;6} \right]\backslash \left\{ 1 \right\};\)
B. \(D = \left[ { – 3; + \infty } \right)\backslash \left\{ 1 \right\};\)
C. \(D = \left[ { – 3;6} \right)\backslash \left\{ 1 \right\};\)
D. \(D = \left( { – \infty ;6} \right]\backslash \left\{ 1 \right\}\)
Câu 3: Cho các cặp bất phương trình sau:
I. \(x – 1 > 0\) và \({x^2}\left( {x – 1} \right) < 0\)
II. \(x – 1 \le 0\) và \(\frac{1}{{{x^2} + 1}}\left( {x – 1} \right) \ge 0\)
III. \(x – 1 \le 0\) và \({x^2}\left( {x – 1} \right) \le 0\)
IV. \(x – 1 \ge 0\) và \({x^2}\left( {x – 1} \right) \ge 0\)
Số cặp bất phương trình tương đương là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu 4: Cho nhị thức bậc nhất \(f\left( x \right) = 23x – 20\). Khẳng định nào sau đây đúng?
A.\(f\left( x \right) > 0\) với \(\forall x \in \mathbb{R}\);
B.\(f\left( x \right) > 0\) với \(\forall x \in \left( { – \infty ;\frac{{20}}{{23}}} \right)\);
C.\(f\left( x \right) > 0\) với \(x > – \frac{5}{2}\);
D.\(f\left( x \right) > 0\) với \(\forall x \in \left( {\frac{{20}}{{23}}; + \infty } \right).\)
Câu 5: Với x thuộc tập hợp nào dưới đây thì nhị thức bậc nhất\(f\left( x \right) = \frac{{2 – x}}{{2x + 1}}\)không âm?
A. \(S = \left( { – \frac{1}{2};2} \right)\);
B. \(S = \left( { – \infty ; – \frac{1}{2}} \right) \cup \left( {2; + \infty } \right)\);
C. \(S = \left( { – \infty ; – \frac{1}{2}} \right) \cup \left[ {2; + \infty } \right)\);
D. \(S = \left( { – \frac{1}{2};2} \right]\).
Câu 6: Miền nghiệm của bất phương trình \[2x + y > 1\] không chứa điểm nào sau đây?
A.\(A\left( {1\,\,;\,\,1} \right);\)
B.\(B\left( {2\,\,;\,\,2} \right)\);
C.\(C\left( {3\,\,;\,\,3} \right)\);
D.\(D\left( { – 1\,\,;\,\, – 1} \right)\).
Câu 7: Miền nghiệm của bất phương trình \(3x – 2y > – 6\) là :
A.
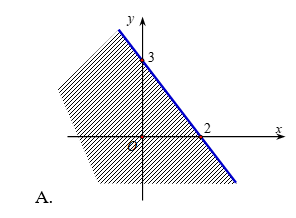
B.
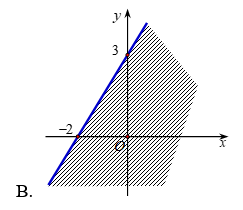
C.
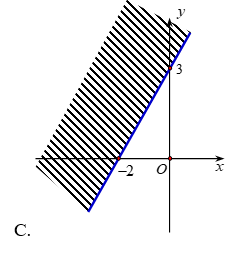
D.
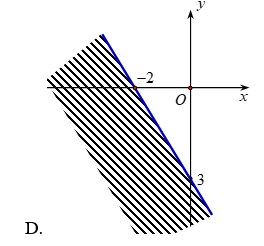
Câu 8: Một công ty cần thuê xe vận chuyển 140 người và 9 tấn hàng hóa. Nơi cho thuê xe chỉ có 10 xe hiệu MITSUBISHI và 9 xe hiệu FORD. Một chiếc xe hiệu MITSUBISHI có thể chở 20 người và 0,6 tấn hàng. Một chiếc xe hiệu FORD có thể chở 10 người và 1,5 tấn hàng. Tiền thuê một xe hiệu MITSUBISHI là 4 triệu đồng, một xe hiệu FORD là 3 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thấp nhất?
A. 4 xe hiệu MITSUBISHI và 5 xe hiệu FORD;
B. 4 xe hiệu MITSUBISHI và 4 xe hiệu FORD;
C. 4 xe hiệu MITSUBISHI và 6 xe hiệu FORD;
D. 5 xe hiệu MITSUBISHI và 4 xe hiệu FORD.
Câu 9: Cho tam thức bậc hai \(f(x) = a{x^2} + b{\rm{x}} + c(a \ne 0),\,\Delta = {b^2} – 4{\rm{a}}c\). Chọn mệnh đề đúng trong các mệnh đề sau.
A. Nếu \(\Delta < 0\) thì f(x) luôn trái dấu với hệ số hệ số a, với mọi \[x \in \mathbb{R}\];
B. Nếu \(\Delta \le 0\) thì f(x) luôn cùng dấu với hệ số hệ số a, với mọi \[x \in \mathbb{R}\];
C. Nếu \(\Delta > 0\) thì f(x) luôn cùng dấu với hệ số hệ số a, với mọi \[x \in \mathbb{R}\];
D. Nếu \(\Delta \ge 0\) thì f(x) luôn cùng dấu với hệ số hệ số a, với mọi \[x \in \mathbb{R}\].
Câu 10: Bảng xét dấu nào sau đây là của tam thức \[f\left( x \right) = – {\rm{ }}{x^2}{\rm{ + }}6x – 9\]?
A.

B.
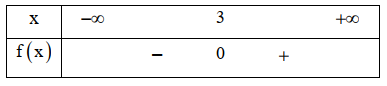
C.
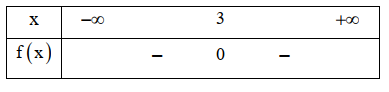
D.

Câu 11: Khi xét dấu biểu thức \(f\left( x \right) = \frac{{{x^2} + 4x – 21}}{{{x^2} – 1}}\) ta có:
A. \(f\left( x \right) > 0\) khi \( – 7 < x < – 1\)hoặc \(1 < x < 3\);
B. \(f\left( x \right) > 0\) khi \(x < – 7\)hoặc \( – 1 < x < 1\) hoặc \(x > 3\);
C. \(f\left( x \right) > 0\) khi \( – 1 < x < 0\)hoặc \(x > 1\);
D. \(f\left( x \right) > 0\) khi \(x > – 1\).
Câu 12: Tìm tập nghiệm S của bất phương trình \( – 2{x^2} – 3x + 2 > 0\).
A. \[{\rm{S}} = \left( { – 2;\frac{1}{2}} \right);\]
B. \[{\rm{S}} = \left( { – \frac{1}{2};2} \right);\]
C. \[{\rm{S}} = ( – \infty ; – 2) \cup \left( {\frac{1}{2}; + \infty } \right);\]
D. \[{\rm{S}} = ( – \infty ; – \frac{1}{2}) \cup (2; + \infty )\].
Câu 13: Góc có số đo 108° đổi ra radian là :
A.\[\frac{{3\pi }}{5};\]
B.\[\frac{\pi }{{10}};\]
C. \[\frac{{3\pi }}{2};\]
D. \[\frac{\pi }{4}.\]
Câu 14: Góc có số đo \[\frac{{2\pi }}{5}\] đổi sang độ là :
A. 240° ;
B. 135° ;
C. 72° ;
D. 270°.
Câu 15: Tính \(Q = \tan {20^0}\tan {70^0} + \sqrt 3 \cot {20^0}\cot {70^0}\)
A. 1;
B. \(\sqrt 3 ;\)
C. \(1 + \sqrt 3 ;\)
D. \(1 – \sqrt 3 .\)
Câu 16: Điều khẳng định nào sau đây là đúng?
A. \(\sin \alpha = \sin \left( {{{180}^o} – \alpha } \right);\)
B. \(\tan \alpha = \tan \left( {{{180}^o} – \alpha } \right);\)
C. \(\cos \alpha = \cos \left( {{{180}^o} – \alpha } \right);\)
D. \(\cot \alpha = \cot \left( {{{180}^o} – \alpha } \right).\)
Câu 17: Trong các khẳng định sau đây, khẳng định nào sai?
A. \(\cos {45^o} = \sin {135^o};\)
B. \(\cos {120^o} = \sin {60^o};\)
C. \(\cos {45^o} = \sin {45^o};\)
D. \(\cos {45^o} = \sin {55^o}.\)
Câu 18: Trong các công thức sau, công thức nào sai?
A. \[\cos 2a = {\cos ^2}a–{\sin ^2}a;\]
B. \[\cos 2a = {\cos ^2}a + {\sin ^2}a;\]
C. \[\cos 2a = 2{\cos ^2}a–1;\]
D. \[\cos 2a = 1–2{\sin ^2}a.\]
Câu 19: Trong các công thức sau, công thức nào đúng?
A. \(\tan \left( {a – b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}};\)
B. \[\tan \left( {a–b} \right) = \tan a – \tan b;\]
C. \(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}};\)
D. \[\tan \left( {a + b} \right) = \tan a + \tan b.\]
Câu 20: Cho \(\sin \alpha = \frac{3}{4}\). Khi đó \(\cos 2\alpha \) bằng:
A. \(\frac{1}{8}\);
B. \(\frac{{\sqrt 7 }}{4}\);
C. \( – \frac{{\sqrt 7 }}{4}\);
D. \( – \frac{1}{8}\).
II. TỰ LUẬN
Bài 1. Giải BPT sau: 3x + 1 > 3 – 2x.
Bài 2. Tìm m để \[\left( {m + 1} \right){x^2} + mx + m < 0,\forall x \in \mathbb{R}\]?
Bài 3.
a) Cho \[\sin \alpha = – \frac{9}{{11}}\], \[\pi < \alpha < \frac{{3\pi }}{2}\]. Tính \[\tan \left( {\frac{\pi }{4} – \alpha } \right)\].
b) Chứng minh đẳng thức \({\sin ^4}x + {\cos ^4}x – \frac{1}{4}\cos 4x = \frac{3}{4}\).
Bài 4.
a) Lập phương trình tham số của đường thẳng d đi qua \(B\left( {7; – 5} \right)\) và vuông góc đường thẳng : \(x + 3y – 6 = 0\).
b) Đi qua điểm M(1 ; 2) có đúng 2 đường tròn tiếp xúc với 2 trục tọa độ. Tính tổng 2 bán kính của 2 đường tròn đó.
–––Hết–––
Đề thi Toán lớp 10 học kì 2 năm 2021 có ma trận (8 đề) – Đề 8
Phòng Giáo dục và Đào tạo …..
Đề thi Học kì 2
Năm học 2021 – 2022
Bài thi môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
(Đề số 8)
I. TRẮC NGHIỆM
Câu 1: Tập nghiệm của bất phương trình \(\frac{{x + 1}}{{3 – 2x}} \le 0\).
A. S =\[\left[ { – 1;\frac{3}{2}} \right]\];
B. S =\(( – \infty ; – 1] \cup \left[ {\frac{3}{2}; + \infty } \right)\);
C. S =\(( – \infty ; – 1{\rm{]}} \cup \left( {\frac{3}{2}; + \infty } \right)\);
D. S =\(\left[ { – 1;\frac{3}{2}} \right)\).
Câu 2: Tập nghiệm của bất phương trình\(\frac{{4x – 3}}{{1 – 2x}} \ge – 1\).
A. S =\[\left[ {\frac{1}{2};1} \right)\];
B. S =\(\left( {\frac{1}{2};1} \right)\);
C. S =\[\left[ {\frac{1}{2};1} \right]\];
D. S =\(\left( {\frac{1}{2};1} \right]\).
Câu 3: Bất phương trình \(\frac{{2x – 5}}{3} > \frac{{x – 3}}{2}\) có tập nghiệm là:
A. S =\(\left( {1; + \infty } \right)\);
B. S =\(\left( {2; + \infty } \right)\);
C. S =\(\left( { – \infty ;1} \right) \cup \left( {2; + \infty } \right)\);
D. S =\(\left( { – \frac{1}{4}; + \infty } \right)\).
Câu 4: Hệ bất phương trình \(\left\{ \begin{array}{l}x – 2 > 2x + 3\\{x^2} – 10x – 25 > 0\end{array} \right.\) có nghiệm là:
A. x > 5;
B. x < – 5;
C. x > – 5;
D. x < 5.
Câu 5: Số đo độ của góc \[\frac{\pi }{4}\] là:
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Câu 6: Góc 18° có số đo bằng rađian là:
A. \(\frac{\pi }{{10}}\);
B. \(\frac{\pi }{{360}}\);
C. \(\frac{\pi }{{18}}\);
D. \(\pi \).
Câu 7: Trong các công thức sau, công thức nào đúng?
A. cos(a – b) = cosa.cosb + sina.sinb;
B. cos(a + b) = cosa.cosb + sina.sinb;
C. sin(a – b) = sina.cosb + cosa.sinb;
D. sin(a + b) = sina.cosb – cos.sinb.
Câu 8: Trong các khẳng định sau khẳng định nào sai?
A. \(\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a – b} \right) + \sin \left( {a + b} \right)} \right]\);
B. \(\sin b\cos a = \frac{1}{2}\left[ {\cos \left( {a – b} \right) + \cos \left( {a + b} \right)} \right]\);
C. \(\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a – b} \right)} \right]\);
D. \(\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a – b} \right) – \cos \left( {a + b} \right)} \right]\).
Câu 9: Công thức nào sau đây sai?
A. \(\tan x.\cot x = 1\);
B. \(1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\);
C. \[\tan x = \frac{{\cos x}}{{\sin x}}\];
D. \(1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}\).
Câu 10: Tính \(\cos \left( {a + \frac{\pi }{3}} \right)\) biết \(\sin a = \sqrt {\frac{1}{3}} \)và \(0 < a < \frac{\pi }{2}\).
A. \(\cos \left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 + 3}}{6}\);
B. \(\cos \left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 – 3}}{6}\);
C. \(\cos \left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 – 2}}{6}\);
D. \(\cos \left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 + 2}}{6}\).
Câu 11: Cho tam giác ABC có \(AB = 4;AC = 6;\cos B = \frac{1}{8}\) và \(\cos C = \frac{3}{4}\). Cạnh BC bằng:
A. 5;
B. \(3\sqrt 3 \);
C. 2;
D. 7.
Câu 12: Trong mặt phẳng Oxy, cho đường thẳng d có phương trình tổng quát : 2x – y + 5 = 0. Một véc tơ pháp tuyến của d.
A. (2; 1);
B. (2; – 1);
C. (1; 2);
D. (1; – 2).
Câu 13: Trong mặt phẳng Oxy, cho phương trình tham số của đường thẳng (d): \(\left\{ \begin{array}{l}x = 5 + t\\y = – 9 – 2t\end{array} \right.\).
Phương trình nào là phương trình tổng quát của (d)?
A.\[2x + y – 1 = 0\];
B. \[2x + y + 1 = 0\];
C. \[x + 2y + 2 = 0\];
D. \[x + 2y – 2 = 0\].
Câu 14: Trong mặt phẳng Oxy, cho phương trình tham số của đường thẳng (d): \[\left\{ \begin{array}{l}x = – 2 – 3t\\y = 3 + 4t\end{array} \right.\]
Véc tơ chỉ phương của đường thẳng d là:
A.\[\left( {4; – 3} \right)\];
B. \[\left( {4;3} \right)\];
C. \[\left( { – 3;4} \right)\];
D. \[\left( { – 3; – 4} \right)\].
Câu 15: Trong mặt phẳng Oxy phương trình nào là phương trình tham số của đường thẳng x – y + 2 = 0:
A. \[\left\{ \begin{array}{l}x = t\\y = 2 + t\end{array} \right.\];
B. \[\left\{ \begin{array}{l}x = 2\\y = t\end{array} \right.\];
C. \[\left\{ \begin{array}{l}x = 3 + t\\y = 1 + t\end{array} \right.\];
D. \[\left\{ \begin{array}{l}x = t\\y = 3 – t\end{array} \right.\].
Câu 16: Hệ số góc của đường thẳng (∆) : \(\left\{ \begin{array}{l}x = 5 + \sqrt 3 t\\y = – 9 – t\end{array} \right.\) là:
A. \[\frac{{ – 1}}{{\sqrt 3 }}\];
B. \[ – \sqrt 3 \];
C. \[\frac{4}{{\sqrt 3 }}\];
D. \[ – \frac{4}{{\sqrt 3 }}\].
Câu 17: Phương trình tổng quát của đường thẳng đi qua 2 điểm A(3; −1) và B(1; 5)
A. 3x − y + 10 = 0;
B. 3x + y − 8 = 0;
C. 3x − y + 6 = 0;
D. −x + 3y + 6 = 0.
Câu 18: Đường tròn \[{x^2} + {y^2} – 2x + 4y + 1 = 0\] tọa độ tâm và bán kính là:
A.I(–1 ; 2), R = 4;
B. I(1 ; – 2), R = 4;
C. I(1 ; – 2), R = 2;
D. I(–1 ; 2), R = 2.
Câu 19: Phương trình tiếp tuyến của đường tròn \(\left( C \right):{x^2} + {y^2} – 2x – 4y – 3 = 0\) tại M(3; 4) là:
A. \(2x + 3y – 18 = 0\);
B. \(x – 4 = 0\);
C. \(3x + 4y – 1 = 0\);
D. \(x + y – 7 = 0\).
Câu 20: Với những giá trị nào của m thì đường thẳng D: 4x + 3y + m = 0 tiếp xúc với đường tròn (C) :\[{x^2} + {y^2} – 9 = 0\].
A. m = 3;
B. m = -3;
C. m = 3 và m = -3;
D. m = 15 và m = -15.
II. TỰ LUẬN
Bài 1. a) Giá trị của biểu thức \[A = \cos \frac{{37\pi }}{{12}}\].
b) Rút gọn biểu thức: A = \[\frac{{{{\tan }^2}a – {{\sin }^2}a}}{{{{\cot }^2}a – {{\cos }^2}a}}.\]
Bài 2. Cho đường tròn (C): x2 + y2 + 8x – 4y + 2 = 0.
a) Tìm tâm và bán kính đường tròn (C).
b) Viết phương trình tiếp tuyến của (C) tại A(–1;5).
Bài 3. Trong mặt phẳng Oxy, cho A(1;1), B(2;–1), C(4;0).
a) Viết phương trình tổng quát của đường thẳng BC, phương trình đường cao AH.
b) Tính diện tích tam giác ABC.
c) Viết phương trình đường tròn tâm A, tiếp xúc với cạnh BC.
Bài 4. Viết phương trình elip có trục nhỏ bằng 10, tâm sai là \(\frac{{12}}{{13}}.\)
–––Hết–––