Câu hỏi và bài tập tích vô hướng của hai vectơ và ứng dụng

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Câu hỏi và bài tập tích vô hướng của hai vectơ và ứng dụng, tài liệu bao gồm 51 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Câu hỏi và bài tập tích vô hướng của hai vectơ và ứng dụng

Chủ đề 7 Tích vô hướng của hai vectơ và ứng dụng

Bài 01: Giá trị lượng giác của một góc bất kỳ

1. Định nghĩa

Với mỗi góc $\alpha \left(0^{°}\le \alpha \le {180}^{°}\right)$ ta xác định một điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \) và giả sử điểm M có tọa độ \(M\left( {{x_0};{y_0}} \right)\). Khi đó ta có định nghĩa:

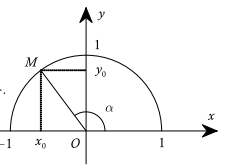
– sin của góc \(\alpha \) là \({y_0}\), kí hiệu \(\sin \alpha  = {y_0}\);

– cosin của góc \(\alpha \) là \({x_0}\), kí hiệu \(\cos \alpha  = {x_0}\);

– tang của góc \(\alpha \) là \(\frac{{{y_0}}}{{{x_0}}}\left( {{x_0} \ne 0} \right)\), kí hiệu \(\tan \alpha  = \frac{{{y_0}}}{{{x_0}}}\);

– cotang của góc \(\alpha \) là \(\frac{{{x_0}}}{{{y_0}}}\left( {{y_0} \ne 0} \right)\), kí hiệu \(\cot \alpha  = \frac{{{x_0}}}{{{y_0}}}\)        

2. Tính chất

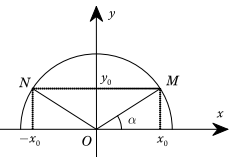
Trên hình bên ta có dây cung NM song song với trục Ox và nếu $\widehat{xON}={180}^{°}-\alpha$. Ta có $y_M=y_N=y_0,x_M=-x_N=x_0$. Do đó

$\sin \alpha =\sin \left({180}^{°}-\alpha \right)$

$\cos \alpha =-\cos \left({180}^{°}-\alpha \right)$

$\tan \alpha =-\tan \left({180}^{°}-\alpha \right)$

$\cot \alpha =-\cot \left({180}^{°}-\alpha \right)$

3. Gía trị lượng giác của các góc đặc biệt

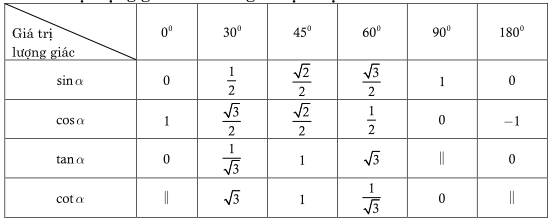
Trong bảng kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Chú ý. Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác.

Chẳng hạn

$\begin{array}{l}\sin {120}^{°}=\sin \left({180}^{°}-{60}^{°}\right)=\sin {60}^{°}=\frac{\sqrt{3}}{2}\\ \cos {135}^{°}=\cos \left({180}^{°}-{45}^{°}\right)=-\cos {45}^{°}=-\frac{\sqrt{2}}{2}\end{array}$

4. Góc giữa hai vecto

a) Định nghĩa

Cho hai vecto \(\overrightarrow a \)và \(\vec b\) đều khác vecto \(\vec 0\). Từ một điểm O bất kì ta vẽ \(\overrightarrow {OA}  = \vec a\) và \(\overrightarrow {OB}  = \vec b\). Góc \(\widehat {AOB}\) với số đo từ \({0^0}\) đến ${180}^{°}$ được gọi là góc giữa hai vectơ \(\vec a\) và \(\vec b\). Ta kí hiệu góc giữa hai vectơ \(\vec a\) và \(\vec b\) là \((\vec a,\vec b)\). Nếu $(\overrightarrow{a},\overrightarrow{b})={90}^{°}$ thì ta nói rằng \(\vec a\) và \(\vec b\) vuông góc với nhau, kí hiệu là \(\vec a \bot \vec b\) hoặc \(\vec b \bot \vec a\).

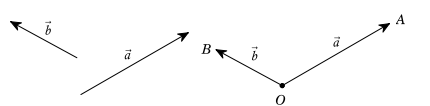
b) Chú ý. Từ định nghĩa ta có \((\vec a,\vec b) = (\vec b,\vec a)\).

Câu hỏi trắc nghiệm

Vấn đề 1. Giá trị lượng giác

Câu 1. Giá trị $\cos {45}^{°}+\sin {45}^{°}$ bằng bao nhiêu?

A. 1 .

B. \(\sqrt 2 \).

C. \(\sqrt 3 \).

D. 0 .

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\left\{\begin{array}{l}\cos {45}^{°}=\frac{\sqrt{2}}{2}\\ \sin {45}^{°}=\frac{\sqrt{2}}{2}\end{array}\to \cos {45}^{°}+\sin {45}^{°}=\sqrt{2}\right.$. Chọn B.

Câu 2. Giá trị của $\tan {30}^{°}+\cot {30}^{°}$ bằng bao nhiêu?

A. \(\frac{4}{{\sqrt 3 }}\).

B. \(\frac{{1 + \sqrt 3 }}{3}\).

C. \(\frac{2}{{\sqrt 3 }}\).

D. 2 .

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT $\left\{\begin{array}{l}\tan {30}^{°}=\frac{1}{\sqrt{3}}\to \tan {30}^{°}+\cot {30}^{°}=\frac{4}{\sqrt{3}}\text{. }\\ \cot {30}^{°}=\sqrt{3}\end{array}\right.$Chọn A

Câu 3. Trong các đẳng thức sau đây đẳng thức nào là đúng?

A. $\sin {150}^{°}=-\frac{\sqrt{3}}{2}$.

B. $\cos {150}^{°}=\frac{\sqrt{3}}{2}$.

C. $\tan {150}^{°}=-\frac{1}{\sqrt{3}}$.

D. $\cot {150}^{°}=\sqrt{3}$.

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\tan {150}^{°}=-\frac{1}{\sqrt{3}}$. Chọn \({\bf{C}}\).

Câu 4. Tính giá trị biểu thức $P=\cos {30}^{°}\cos {60}^{°}-\sin {30}^{°}\sin {60}^{°}$.

A. \(P = \sqrt 3 \).

B. \(P = \frac{{\sqrt 3 }}{2}\).

C. \(P = 1\).

D. \(P = 0\).

Lời giải. Vì ${30}^{°}$ và ${60}^{°}$ là hai góc phụ nhau nên $\left\{\begin{array}{l}\sin {30}^{°}=\cos {60}^{°}\\ \sin {60}^{°}=\cos {30}^{°}\end{array}\right.$$P=\cos {30}^{°}\cos {60}^{°}-\sin {30}^{°}\sin {60}^{°}=\cos {30}^{°}\cos {60}^{°}-\cos {60}^{°}\cos {30}^{°}=0$. Chọn \({\bf{D}}.\)

Câu 5. Tính giá trị biểu thức $P=\sin {30}^{°}\cos {60}^{°}+\sin {60}^{°}\cos {30}^{°}$.

A. \(P = 1\).

B. \(P = 0\).

C. \(P = \sqrt 3 \).

D. \(P =  – \sqrt 3 \).

Lời giải. Vì ${30}^{°}$ và ${60}^{°}$ là hai góc phụ nhau nên $\left\{\begin{array}{l}\sin {30}^{°}=\cos {60}^{°}\\ \sin {60}^{°}=\cos {30}^{°}\end{array}\right.$$P=\sin {30}^{°}\cos {60}^{°}+\sin {60}^{°}\cos {30}^{°}={\cos }^2{60}^{°}+{\sin }^2{60}^{°}=1$. Chọn A.

Câu 6. Trong các đẳng thức sau, đẳng thức nào sai?

A. $\sin {45}^{°}+\cos {45}^{°}=\sqrt{2}$.

B. $\sin {30}^{°}+\cos {60}^{°}=1$.

C. $\sin {60}^{°}+\cos {150}^{°}=0$.

D. $\sin {120}^{°}+\cos {30}^{°}=0$.

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\left\{\begin{array}{l}\cos {30}^{°}=\frac{\sqrt{3}}{2}\\ \sin {120}^{°}=\frac{\sqrt{3}}{2}\end{array}\to \cos {30}^{°}+\sin {120}^{°}=\sqrt{3}\right.$. Chọn D

Câu 7. Trong các đẳng thức sau, đẳng thức nào sai?

A. $\sin 0^{°}+\cos 0^{°}=0$.

B. $\sin {90}^{°}+\cos {90}^{°}=1$.

C. $\sin {180}^{°}+\cos {180}^{°}=–1$.

D. $\sin {60}^{°}+\cos {60}^{°}=\frac{\sqrt{3}+1}{2}$.

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\left\{\begin{array}{l}\cos 0^0=1\\ \sin 0^0=0\end{array}\to \cos 0^{°}+\sin 0^{°}=1\right.$. Chọn A.

Câu 8. Trong các khẳng định sau đây, khẳng định nào sai?

A. $\cos {45}^{°}=\sin {45}^{°}$.

B. $\cos {45}^{°}=\sin {135}^{°}$

C. $\cos {30}^{°}=\sin {120}^{°}$.

D. $\sin {60}^{°}=\cos {120}^{°}$.

Lời giải. Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\left\{\begin{array}{l}\cos {120}^{°}=-\frac{1}{2}\\ \sin {60}^{°}=\frac{\sqrt{3}}{2}\end{array}\right.$ Chọn D.

Câu 9. Tam giác ABC vuông ở A có góc $\widehat{B}={30}^{°}$. Khẳng định nào sau đây là sai?

A. \(\cos B = \frac{1}{{\sqrt 3 }}\).

B. \(\sin C = \frac{{\sqrt 3 }}{2}\).

C. \(\cos C = \frac{1}{2}\).

D. \(\sin B = \frac{1}{2}\).

Lời giải. Từ giả thiết suy ra $\widehat{C}={60}^{°}$.

Bằng cách tra bảng giá trị lượng giác của các góc đặc biệt hay dùng MTCT ta được $\cos B=\cos {30}^{°}=\frac{\sqrt{3}}{2}$. Chọn A.

Câu 10. Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?

A. \(\sin \widehat {BAH} = \frac{{\sqrt 3 }}{2}\).

B. \(\cos \widehat {BAH} = \frac{1}{{\sqrt 3 }}\).

C. \(\sin \widehat {ABC} = \frac{{\sqrt 3 }}{2}\).

D. \(\sin \widehat {AHC} = \frac{1}{2}\).

Lời giải. Ta có $\widehat{BAH}={30}^{°}\to \left\{\begin{array}{l}\sin \widehat{BAH}=\frac{1}{2}\\ \cos \widehat{BAH}=\frac{\sqrt{3}}{2}\end{array}\right.$

Do đó A sai; B sai

Ta có $\widehat{ABC}={60}^{°}\to \sin \widehat{ABC}=\frac{\sqrt{3}}{2}$. Do đó C đúng. Chọn C.

Vấn đề 2: Hai góc bù nhau – hai góc phụ nhau

Câu 11. Trong các đẳng thức sau, đẳng thức nào đúng?

A. $\sin \left({180}^{°}-\alpha \right)=-\cos \alpha$.

B. $\sin \left({180}^{°}-\alpha \right)=-\sin \alpha$.

C. $\sin \left({180}^{°}-\alpha \right)=\sin \alpha$.

D. $\sin \left({180}^{°}-\alpha \right)=\cos \alpha$..

Lời giải. Hai góc bù nhau \(\alpha \) và $\left({180}^{°}-\alpha \right)$ thì cho có giá trị của sin bằng nhau.

Chọn C.

Câu 12. Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?

A. \(\sin \alpha  = \sin \beta \).

B. \(\cos \alpha  =  – \cos \beta \).

C. \(\tan \alpha  =  – \tan \beta \).

D. \(\cot \alpha  = \cot \beta \).

Lời giải. Hai góc bù nhau \(\alpha \) và \(\beta \) thì cho có giá trị của sin bằng nhau, các giá trị còn lại thì đối nhau. Do đó \({\rm{D}}\) sai. Chọn \({\bf{D}}\).

Câu 13. Tính giá trị biểu thức $P=\sin {30}^{°}\cos {15}^{°}+\sin {150}^{°}\cos {165}^{°}$.

A. \(P =  – \frac{3}{4}\).

B. \(P = 0\).

C. \(P = \frac{1}{2}\).

D. \(P = 1\).

Lời giải. Hai góc ${30}^{°}$ và ${150}^{°}$ bù nhau nên $\sin {30}^{°}=\sin {150}^{°}$;

Hai góc ${15}^{°}$ và ${165}^{°}$ bù nhau nên $\cos {15}^{°}=-\cos {165}^{°}$.

Do đó $P=\sin {30}^{°}\cos {15}^{°}+\sin {150}^{°}\cos {165}^{°}=\sin {150}^{°}.\left(-\cos {165}^{°}\right)+\sin {150}^{°}\cos {165}^{°}=0$.

Chọn B.

Câu 14. Cho hai góc \(\alpha \) và \(\beta \) với $\alpha +\beta ={180}^{°}$. Tính giá trị của biểu thức \(P = \cos \alpha \cos \beta  – \sin \beta \sin \alpha .\)

A. \(P = 0\).

B. \(P = 1\).

C. \(P =  – 1\).

D. \(P = 2\).

Lời giải. Hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha  = \sin \beta ;\cos \alpha  =  – \cos \beta \).

Do đó, \(P = \cos \alpha \cos \beta  – \sin \beta \sin \alpha  =  – {\cos ^2}\alpha  – {\sin ^2}\alpha  =  – \left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right) =  – 1\). Chọn C.

Câu 15. Cho tam giác ABC. Tính \(P = \sin A \cdot \cos (B + C) + \cos A \cdot \sin (B + C)\).

A. \(P = 0\).

B. \(P = 1\).

C. \(P =  – 1\).

D. \(P = 2\).

Lời giải. Giả sử \(\hat A = \alpha ;\hat B + \hat C = \beta \). Biểu thức trở thành \(P = \sin \alpha \cos \beta  + \cos \alpha \sin \beta \).

Trong tam giác AB C, có $\widehat{A}+\widehat{B}+\widehat{C}={180}^{°}\Rightarrow \alpha +\beta ={180}^{°}$.

Do hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha  = \sin \beta ;\cos \alpha  =  – \cos \beta \).

Do đó, \(P = \sin \alpha \cos \beta  + \cos \alpha \sin \beta  =  – \sin \alpha \cos \alpha  + \cos \alpha \sin \alpha  = 0\). Chọn A.

Câu 16. Cho tam giác ABC. Tính \(P = \cos A \cdot \cos (B + C) – \sin A \cdot \sin (B + C)\).

A. \(P = 0\).

B. \(P = 1\).

C. \(P =  – 1\).

D. \(P = 2\).

Lời giải. Giả sử \(\hat A = \alpha ;\hat B + \hat C = \beta \). Biểu thức trở thành \(P = \cos \alpha \cos \beta  – \sin \alpha \sin \beta \).

Trong tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}={180}^{°}\Rightarrow \alpha +\beta ={180}^{°}$.

Do hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha  = \sin \beta ;\cos \alpha  =  – \cos \beta \).

Do đó, \(P = \cos \alpha \cos \beta  – \sin \alpha \sin \beta  =  – {\cos ^2}\alpha  – {\sin ^2}\alpha  =  – \left( {{{\sin }^2}\alpha  + {{\cos }^2}\alpha } \right) =  – 1\). Chọn C.

Câu 17. Cho hai góc nhọn \(\alpha \) và \(\beta \) phụ nhau. Hệ thức nào sau đây là sai?

A. \(\sin \alpha  =  – \cos \beta \).

B. \(\cos \alpha  = \sin \beta \).

C. \(\tan \alpha  = \cot \beta \).

D. \(\cot \alpha  = \tan \beta \).

Lời giải. Hai góc nhọn \(\alpha \) và \(\beta \) phụ nhau thì \(\sin \alpha  = \cos \beta ;\cos \alpha  = \sin \beta ;\tan \alpha  = \cot \beta \); \(\cot \alpha  = \tan \beta \). Chọn A.

Câu 18. Tính giá trị biểu thức $S={\sin }^2{15}^{°}+{\cos }^2{20}^{°}+{\sin }^2{75}^{°}+{\cos }^2{110}^{°}$.

A. \(S = 0\).

B. \(S = 1\).

C. \(S = 2\).

D. \(S = 4\).

Lời giải. Hai góc ${15}^{°}$ và ${75}^{°}$) phụ nhau nên $\sin {75}^{°}=\cos {15}^{°}$.

Hai góc ${20}^{°}$ và ${110}^{°}$ hơn kém nhau ${90}^{°}$ nên $\cos {110}^{°}=-\sin {20}^{°}$.

Do đó, $S={\sin }^2{15}^{°}+{\cos }^2{20}^{°}+{\sin }^2{75}^{°}+{\cos }^2{110}^{°}$

$={\sin }^2{15}^{°}+{\cos }^{2}20+{\cos }^2{15}^{°}+{\left(-\sin {20}^{°}\right)}^2=\left({\sin }^2{15}^{°}+{\cos }^2{15}^{°}\right)+\left({\sin }^2{20}^{°}+{\cos }^2{20}^{°}\right)=2$

Chọn C.

Câu 19. Cho hai góc \(\alpha \) và \(\beta \) với $\alpha +\beta ={90}^{°}$. Tính giá trị của biểu thức \(P = \sin \alpha \cos \beta  + \sin \beta \cos \alpha \).

A. \(P = 0\).

B. \(P = 1\).

C. \(P =  – 1\).

D. \(P = 2\).

Lời giải. Hai góc \(\alpha \) và \(\beta \) phụ nhau nên \(\sin \alpha  = \cos \beta ;\cos \alpha  = \sin \beta \).

Do đó, \(P = \sin \alpha \cos \beta  + \sin \beta \cos \alpha  = {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\). Chọn B.

Câu 20. Cho hai góc \(\alpha \) và \(\beta \) với $\alpha +\beta ={90}^{°}$. Tính giá trị của biểu thức \(P = \cos \alpha \cos \beta  – \sin \beta \sin \alpha \).

A. \(P = 0\).

B. \(P = 1\).

C. \(P =  – 1\).

D. \(P = 2\).

Lời giải. Hai góc \(\alpha \) và \(\beta \) phụ nhau nên \(\sin \alpha  = \cos \beta ;\cos \alpha  = \sin \beta \).

Do đó, \(P = \cos \alpha \cos \beta  – \sin \beta \sin \alpha  = \cos \alpha \sin \alpha  – \cos \alpha \sin \alpha  = 0\). Chọn A.

Xem thêm