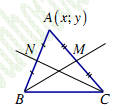Bài tập về Ứng dụng phương trình đường thẳng trong các bài toán tam giác chọn lọc

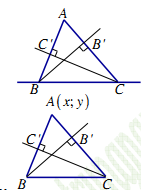
1. Loại 1. Cho cạnh BC và phương trình hai đường cao  $BB‘,CC;:$

 Tìm  $B=BC\cap BB‘,C=BC\cap CC‘$

 Viết AB: qua B và  $AB\perp CC‘$

 Viết AC: qua C và  $AC\perp BB‘$

 Xác định A:  $A=AB\cap AC$

2. Loại 2. Cho điểm A và phương trình hai đường cao  $BB‘,CC;:$

 Viết AB: qua A và  $AB\perp CC‘$

 Viết AC: qua A và  $AC\perp BB‘$

 Xác định B, C:  $B=BC\cap BB‘,C=AC\cap CC‘$

3. Loại 3. Cho điểm A và phương trình hai đường trung tuyến BM, CN:

 Tìm C:

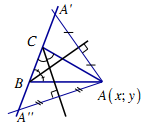
 $M\in BM\Rightarrow M$ có tọa độ theo tham số t

M là trung điểm AC $\Rightarrow$ tọa độ C theo t

 Thay tọa độ C vào  $CN\Rightarrow t\Rightarrow C$

 Tìm B:

$N\in CN\Rightarrow N$  có tọa độ theo tham số t’

N là trung điểm AB $\Rightarrow$ tọa độ B theo t’

 Thay tọa độ B vào  $BM\Rightarrow t‘\Rightarrow B$

4. Loại 4. Cho điểm A và phương trình hai đường phân giác BD, CF

 Gọi $A‘$ đối xứng với A qua BD

 $A‘\in BC.$ Tìm  $A‘$

 Gọi $A‘‘$ đối xứng với A qua CF

$\Rightarrow A‘‘\in BC.$  Tìm  $A‘‘$

 Viết phương trình cạnh BC

 Xác định B, C: $B=BC\cap BD,C=BC\cap CF$

Chú ý: Các bài toán cho kết hợp giữa đường cao, phân giác, trung tuyến đều dựa vào các giải các bài toán trên.

1.59 Cho $\Delta ABC,$ biết phương trình một cạnh và hai đường cao. Viết phương trình hai cạnh còn lại, với:

(1)  $BC:5x-3y+2=0,BB‘:4x-3y+1=0,CC‘:7x+2y-22=0$

(2) $BC:x-y+2=0,BB‘:2x-7y-6=0,CC‘:7x-2y-1=0$

(3) $BC:5x-3y+2=0,BB‘:2x-y-1=0,CC‘:x+3y-1=0$

1.60 Cho $\Delta ABC,$ biết tọa độ một đỉnh và phương trình hai đường cao. Viết phương trình các cạnh

của tam giác đó, với:

$A\left(1;0\right),BB‘:x-2y+1=0,CC‘:3x+y-1=0$

1.61 Cho $\Delta ABC,$ biết tọa độ một đỉnh và phương trình hai đường trung tuyến. Viết phương trình các

cạnh của tam giác đó, với:

$A\left(3;9\right),BM:3x-4y+9=0,CN:y-6=0$

1.62 Cho $\Delta ABC,$ biết phương trình một cạnh AB và hai đường trung tuyến AM, BN. Viết

phương trình hai cạnh còn lại, với:

(1)  $AB:x-2y+7=0,AM:x+y-5=0,BN:2x+y-11=0$

(2) $AB:x-y+1=0,AM:2x+3y=0,BN:2x+6y+3=0$