20 câu Trắc nghiệm Giải tam giác và ứng dụng thực tế (Chân trời sáng tạo 2023) có đáp án

Trắc nghiệm Toán 10 Bài 3: Giải tam giác và ứng dụng thực tế

I. Thông hiểu

Câu 1. Cho ∆ABC có AB = 4, AC = 5 và $\cos A = \frac{3}{5}$ . Độ dài đường cao kẻ từ A bằng:

A. $\frac{16 \sqrt{17}}{17}$ ;

B. $\frac{16 \sqrt{29}}{29}$ ;

C. 8;

D. 10.

Hướng dẫn giải

Đáp án: A

Giải thích:

Theo định lí côsin, ta có

BC² = AB² + AC² – 2.AB.AC.cosA

$= 4^{2} + 5^{2} - 2.4.5. \frac{3}{5} = 17$ .

Suy ra $B C = \sqrt{17}$ .

Nửa chu vi ∆ABC là:

$p = \frac{A B + A C + B C}{2} = \frac{4 + 5 + \sqrt{17}}{2} = \frac{9 + \sqrt{17}}{2}$ .

Diện tích ∆ABC là:

$S = \sqrt{p (p - A B) (p - A C) (p - B C)}$

$= \sqrt{\frac{9 + \sqrt{17}}{2} (\frac{9 + \sqrt{17}}{2} - 4) (\frac{9 + \sqrt{17}}{2} - 5) (\frac{9 + \sqrt{17}}{2} - \sqrt{17})}$

= 8 (đơn vị diện tích).

$T a c ó : S = \frac{1}{2} . B C . h_{a} \Leftrightarrow 8 = \frac{1}{2} . \sqrt{17} . h_{a} \Leftrightarrow h_{a} = \frac{16 \sqrt{17}}{17}$

Vậy ta chọn đáp án A.

Câu 2. Cho ∆ABC nội tiếp đường tròn bán kính bằng 3, biết $\hat{A} = 30 °, \hat{B} = 45 °$ . Độ dài bán kính đường tròn nội tiếp ∆ABC gần giá trị nào nhất?

A. 0,88;

B. 0,94;

C. 1,25;

D. 2,15.

Hướng dẫn giải

Đáp án: B

Giải thích:

Bán kính đường tròn ngoại tiếp ∆ABC là R = 3.

∆ABC có $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - (\hat{A} + \hat{B}) = 180 ° - (30 ° + 45 °) = 105 °$ .

Theo hệ quả định lí sin, ta có:

⦁ a = 2R.sinA = 2.3.sin30° = 3.

⦁ b = 2R.sinB = 2.3.sin45° = $3 \sqrt{2}$ .

⦁ c = 2R.sinC = 2.3.sin105° = $\frac{3 \sqrt{6} + 3 \sqrt{2}}{2}$ .

Nửa chu vi của ∆ABC là:

$p = \frac{a + b + c}{2} = \frac{3 + 3 \sqrt{2} + \frac{3 \sqrt{6} + 3 \sqrt{2}}{2}}{2} = \frac{6 + 9 \sqrt{2} + 3 \sqrt{6}}{4}$ .

Ta có S = pr = $\frac{1}{2}$ ab.sinC

$\Leftrightarrow \frac{6 + 9 \sqrt{2} + 3 \sqrt{6}}{4} . r = \frac{1}{2} .3.3 \sqrt{2} . \sin 105 °$

$\Leftrightarrow \frac{6 + 9 \sqrt{2} + 3 \sqrt{6}}{4} . r = \frac{9 + 9 \sqrt{3}}{4}$

⇔ r ≈ 0,94.

Vậy ta chọn phương án B.

Câu 3. Cho ∆ABC có $a = 2 \sqrt{3}, b = 2 \sqrt{2}, c = \sqrt{6} - \sqrt{2}$ . Góc lớn nhất của ∆ABC bằng:

A. 80°;

B. 90°;

C. 120°;

D. 150°.

Hướng dẫn giải

Đáp án: C

Giải thích:

Vì nên c < b < a.

Do đó $\hat{C} < \hat{B} < \hat{A}$ .

Tức là, $\hat{A}$ lớn nhất.

Theo hệ quả định lí côsin, ta có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{{(2 \sqrt{2})}^{2} + {(\sqrt{6} - \sqrt{2})}^{2} - {(2 \sqrt{3})}^{2}}{2.2 \sqrt{2} . (\sqrt{6} - \sqrt{2})} = - \frac{1}{2}$ .

Suy ra $\hat{A} = 120 °$ .

Vậy ta chọn phương án C.

Câu 4. Cho ∆ABC. Khẳng định nào sau đây đúng?

A. $\cot A = \frac{b^{2} + c^{2} - a^{2}}{4 S}$ ;

B. $\cot A = \frac{b^{2} + c^{2} + a^{2}}{4 S}$ ;

C. $\cot A = \frac{b^{2} + c^{2} - a^{2}}{S}$ ;

D. $\cot A = \frac{b^{2} + c^{2} - a^{2}}{2 S}$ .

Hướng dẫn giải

Đáp án: A

Giải thích:

Theo hệ quả định lí côsin, ta có $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ .

Diện tích ∆ABC là: $S = \frac{1}{2} b c . \sin A$ .

Ta có $\cot A = \frac{\cos A}{\sin A} = \frac{b^{2} + c^{2} - a^{2}}{2 b c . \sin A}$

$= \frac{b^{2} + c^{2} - a^{2}}{4. \frac{1}{2} b c . \sin A} = \frac{b^{2} + c^{2} - a^{2}}{4 S}$

Vậy ta chọn phương án A.

Câu 5. Cho ∆ABC thỏa mãn sinC = 2sinB.cosA. Khi đó ∆ABC là:

A. Tam giác tù;

B. Tam giác đều;

C. Tam giác vuông cân;

D. Tam giác cân.

Hướng dẫn giải

Đáp án: D

Giải thích:

• Theo hệ quả định lí sin, ta có:

$\sin C = \frac{c}{2 R}$ và $\sin B = \frac{b}{2 R}$ .

• Theo hệ quả của định lí côsin, ta có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ .

• Ta có sinC = 2sinB.cosA

$\Leftrightarrow \frac{c}{2 R} = 2. \frac{b}{2 R} . \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\Leftrightarrow c = 2 b . \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

$\Leftrightarrow c = \frac{b^{2} + c^{2} - a^{2}}{c}$

⇔ c2 = b2 + c2 – a2

⇔ b2 = a2

⇔ b = a (vì a, b > 0)

Hay AC = BC.

Suy ra ∆ABC cân tại C.

Vậy ta chọn phương án D.

Câu 6. Cho ∆ABC biết b = 32, c = 45, $\hat{A} = 87 °$ . Khẳng định nào sau đây đúng?

A. a ≈ 53,8, $\hat{B} \approx 37 °, \hat{C} \approx 56 °$ ;

B. a ≈ 2898,3, $\hat{B} \approx 37 °, \hat{C} \approx 56 °$ ;

C. a ≈ 53,8, $\hat{B} \approx 56 °, \hat{C} \approx 37 °$ ;

D. a ≈ 55,2, $\hat{B} \approx 37 °, \hat{C} \approx 56 °$ ;.

Hướng dẫn giải

Hướng dẫn giải

Đáp án: A

Giải thích:

Áp dụng định lí côsin cho DABC, ta có:

a² = b² + c² – 2bc.cosA

= 322 + 452 – 2.32.45.cos87°

≈ 2898,3

Suy ra a ≈ $\sqrt{2898, 3}$ ≈ 53,8.

Theo định lí sin, ta có $\frac{a}{\sin A} = \frac{b}{\sin B}$

Suy ra $\sin B = \frac{b . \sin A}{a} \approx \frac{32. \sin 87 °}{53, 8} \approx 0, 6$ .

Do đó $\hat{B} \approx 37 °$

( $\hat{B} \approx 180 ° - 37 ° = 143 °$ không thỏa mãn do $\hat{A} + \hat{B} \approx 87 ° + 143 ° = 230 ° > 180 °)$

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - (\hat{A} + \hat{B}) \approx 180 ° - (87 ° + 37 °) = 56 °$ .

Vậy a ≈ 53,8, $\hat{B} \approx 37 °, \hat{C} \approx 56 °$ .

Do đó ta chọn phương án A.

Câu 7. Cho ∆ABC biết $\hat{A} = 60 °, \hat{B} = 40 °$ , c = 14. Khẳng định nào sau đây sai?

A. $\hat{C} = 80 °$ ;

B. a ≈ 12,3;

C. b ≈ 9,1;

D. Cả A và C đều sai.

Hướng dẫn giải

Đáp án: D

Giải thích:

⦁ ∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - (\hat{A} + \hat{B}) = 180 ° - (60 ° + 40 °) = 80 °$ .

Do đó phương án A đúng.

⦁ Theo định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ .

Suy ra $a = \frac{c . \sin A}{\sin C} = \frac{14. \sin 60 °}{\sin 80 °} \approx 12, 3$ .

Do đó phương án B đúng.

Ta có $\frac{b}{\sin B} = \frac{c}{\sin C}$

Suy ra $b = \frac{c . \sin B}{\sin C} = \frac{14. \sin 40 °}{\sin 80 °} \approx 9, 1$

Do đó phương án C đúng, phương án D sai.

Vậy ta chọn phương án D.

Câu 8. Cho ∆ABC biết $a = \sqrt{6}$ , b = 2, $c = 1 + \sqrt{3}$ . Khẳng định nào sau đây đúng nhất?

A. $\hat{A} = 60 °$ ;

B. $\hat{B} = 45 °$ ;

C. $\hat{C} = 75 °$ ;

D. Cả A, B, C đều đúng.

Hướng dẫn giải

Đáp án: D

Giải thích:

Theo hệ quả của định lí côsin, ta có:

⦁ $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{2^{2} + {(1 + \sqrt{3})}^{2} - {(\sqrt{6})}^{2}}{2.2. (1 + \sqrt{3})} = \frac{1}{2}$ .

Suy ra $\hat{A} = 60 °$ .

⦁ $\cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c} = \frac{{(\sqrt{6})}^{2} + {(1 + \sqrt{3})}^{2} - 2^{2}}{2. \sqrt{6} . (1 + \sqrt{3})} = \frac{\sqrt{2}}{2}$ .

Suy ra $\hat{B} = 45 °$ .

⦁ $\cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} = \frac{{(\sqrt{6})}^{2} + 2^{2} - {(1 + \sqrt{3})}^{2}}{2. \sqrt{6} .2} = \frac{\sqrt{6} - \sqrt{2}}{4}$ .

Suy ra $\hat{C} = 75 °$ .

Vậy ta chọn phương án D.

Câu 9. Cho $\hat{A} = 120 °, \hat{B} = 45 °$ , R = 2. Khẳng định nào sau đây sai?

A. $B C = 2 \sqrt{2}, A C = 2 \sqrt{3}, A B = \sqrt{6} + \sqrt{2}, \hat{C} = 15 °$ ;

B. $B C = 2 \sqrt{3}, A C = 2 \sqrt{2}, A B = \sqrt{6} + \sqrt{2}, \hat{C} = 15 °$ ;

C. $B C = 2 \sqrt{3}, A C = 2 \sqrt{2}, A B = \sqrt{6} - \sqrt{2}, \hat{C} = 15 °$ ;

D. $B C = 2 \sqrt{2}, A C = 2 \sqrt{3}, A B = \sqrt{6} - \sqrt{2}, \hat{C} = 15 °$

Hướng dẫn giải

Đáp án: C

Giải thích:

Theo hệ quả định lí sin, ta có:

⦁ BC = 2R.sinA = 2.2.sin120° = $2 \sqrt{3}$ .

⦁ AC = 2R.sinB = 2.2.sin45° = $2 \sqrt{2}$ .

Theo định lí côsin, ta có BC2 = AC2 + AB2 – 2.AC.AB.cosA

Suy ra ${(2 \sqrt{3})}^{2} = {(2 \sqrt{2})}^{2} + A B^{2} - 2.2 \sqrt{2} . A B . \cos 120 °$

Khi đó $A B^{2} + 2 \sqrt{2} . A B - 4 = 0$

Vì vậy $A B = \sqrt{6} - \sqrt{2}$ hoặc $A B = - \sqrt{6} - \sqrt{2}$

Vì AB là độ dài một cạnh của ∆ABC nên ta có AB > 0.

Do đó ta nhận $A B = \sqrt{6} - \sqrt{2}$ .

∆ABC có $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{C} = 180 ° - (\hat{A} + \hat{B}) = 180 ° - (120 ° + 45 °) = 15 °$ .

Vậy ta chọn phương án C.

Câu 10. Cho ∆ABC, biết $\hat{A} = 60 °$ , $h_{c} = 2 \sqrt{3}$ , R = 6. Khẳng định nào sau đây đúng?

A. $a = 6 \sqrt{3}, b = 2 + 4 \sqrt{6}, c = 4;$ ;

B. $a = 6 \sqrt{3}, b = 4, c = 2 + 4 \sqrt{6}$

C. $a = 6 \sqrt{3}, b = 4, c = 2 + \sqrt{6};$

D. $a = 6 \sqrt{3}, b = 2 + \sqrt{6}, c = 4$

Hướng dẫn giải

Đáp án: B

Giải thích:

⦁ Theo hệ quả định lí sin, ta có:

a = 2R.sinA = 2.6.sin60° = $6 \sqrt{3}$ .

⦁ Ta có S = $\frac{1}{2} c h_{c} = \frac{1}{2} b c \sin A$ .

Suy ra hc = b.sinA

Do đó $b = \frac{h_{c}}{\sin A} = \frac{2 \sqrt{3}}{\sin 60 °} = 4$ .

⦁ Theo định lí côsin, ta có a2 = b2 + c2 – 2bc.cosA

Suy ra $|{(6 \sqrt{3})}^{2} = 4^{2} + c^{2} - 2.4. c . \cos 60 °|$

Khi đó c² – 4c – 92 = 0

Vì vậy $c = 2 + 4 \sqrt{6}$ hoặc $c = 2 - 4 \sqrt{6}$ .

Vì c là độ dài một cạnh của ∆ABC nên c > 0.

Do đó ta nhận $c = 2 + 4 \sqrt{6}$ .

Vậy ta chọn phương án B.

III. Vận dụng

Câu 1. Cho ∆ABC thỏa mãn sin2A = sinB.sinC. Khẳng định nào sau đây đúng nhất?

A. a² = bc;

B. $\cos A \geq \frac{1}{2}$ ;

C. Cả A và B đều đúng;

D. Cả A và B đều sai.

Hướng dẫn giải

Đáp án: C

Giải thích:

• Theo hệ quả định lí sin ta có:

$\sin A = \frac{a}{2 R}$ , $\sin B = \frac{b}{2 R}$ và $\sin C = \frac{c}{2 R}$ .

Ta có sin2A = sinB.sinC.

$\Leftrightarrow {(\frac{a}{2 R})}^{2} = \frac{b}{2 R} . \frac{c}{2 R}$

$\Leftrightarrow \frac{a^{2}}{{(2 R)}^{2}} = \frac{b c}{{(2 R)}^{2}}$

⇔ a2 = bc.

Do đó phương án A đúng.

• Theo hệ quả của định lí côsin, ta có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{b^{2} + c^{2} - b c}{2 b c}$ .

Áp dụng bất đẳng thức Cauchy cho hai số b, c > 0, ta được b2 + c2 ≥ 2bc.

Do đó ta có $\cos A = \frac{b^{2} + c^{2} - b c}{2 b c} \geq \frac{2 b c - b c}{2 b c} = \frac{b c}{2 b c} = \frac{1}{2}$ .

Vì vậy $\cos A \geq \frac{1}{2}$ .

Do đó phương án B đúng.

Vậy ta chọn phương án C.

Câu 2. Cho ∆ABC thỏa mãn $\sin A = \frac{\sin B + \sin C}{\cos B + \cos C}$ . Khi đó ∆ABC là:

A. Tam giác vuông;

B. Tam giác cân;

C. Tam giác tù;

D. Tam giác đều.

Hướng dẫn giải

Đáp án: A

Giải thích:

• Theo hệ quả của định lí côsin, ta có:

$\cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}$ và $\cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$ .

• Theo hệ quả định lí sin, ta có:

$s i n A = \frac{a}{2 R}; s i n B = \frac{b}{2 R}; s i n C = \frac{c}{2 R}$ .

• Ta có $\sin A = \frac{\sin B + \sin C}{\cos B + \cos C}$

⇔ sinA(cosB + cosC) = sinB + sinC

$\Leftrightarrow \frac{a}{2 R} . (\frac{a^{2} + c^{2} - b^{2}}{2 a c} + \frac{a^{2} + b^{2} - c^{2}}{2 a b}) = \frac{b}{2 R} + \frac{c}{2 R}$

$\Leftrightarrow \frac{a}{2 R} . \frac{1}{2 a} (\frac{a^{2} + c^{2} - b^{2}}{c} + \frac{a^{2} + b^{2} - c^{2}}{b}) = \frac{b + c}{2 R}$

$\Leftrightarrow \frac{1}{2} (\frac{a^{2} + c^{2} - b^{2}}{c} + \frac{a^{2} + b^{2} - c^{2}}{b}) = b + c$

$\Leftrightarrow \frac{b (a^{2} + c^{2} - b^{2}) + c (a^{2} + b^{2} - c^{2})}{b c} = 2 (b + c)$

⇔ a²b + bc² – b³ + a²c + b²c – c³ = 2b²c + 2bc²

⇔ b³ + c³ – (a²b + a²c) + (b²c + bc²) = 0

⇔ (b + c)(b² – bc + c²) – a²(b + c) + bc(b + c) = 0

⇔ (b + c)(b² – bc + c² – a² + bc) = 0

⇔ (b + c)(b² + c² – a²) = 0

⇔ b + c = 0 (vô lí vì b, c > 0) hoặc b² + c² = a²

⇔ AC² + AB² = BC²

Áp dụng định lí Pytago đảo, ta được ∆ABC vuông tại A.

Vậy ta chọn phương án A.

Câu 3. Cho ∆ABC có a.sinA + b.sinB + c.sinC = h_a + h_b + h_c. Khi đó ∆ABC là:

A. Tam giác cân;

B. Tam giác đều;

C. Tam giác thường;

D. Tam giác vuông.

Hướng dẫn giải

Đáp án: B

Giải thích:

Diện tích ∆ABC là: $S = \frac{1}{2} a . h_{a} = \frac{1}{2} b . h_{b} = \frac{1}{2} c . h_{c}$ .

Suy ra $h_{a} = \frac{2 S}{a}; h_{b} = \frac{2 S}{b}; h_{c} = \frac{2 S}{c}$ .

Diện tích ∆ABC là:

$S = \frac{1}{2} b c . \sin A = \frac{1}{2} a c . \sin B = \frac{1}{2} a b . \sin C$ .

Suy ra $\sin A = \frac{2 S}{b c}; \sin B = \frac{2 S}{a c}; \sin C = \frac{2 S}{a b}$ .

Ta có a.sinA + b.sinB + c.sinC = h_a + h_b + h_c

$\Leftrightarrow a . \frac{2 S}{b c} + b . \frac{2 S}{a c} + c . \frac{2 S}{a b} = \frac{2 S}{a} + \frac{2 S}{b} + \frac{2 S}{c}$

$\Leftrightarrow 2 S . (\frac{a}{b c} + \frac{b}{a c} + \frac{c}{a b}) = 2 S . (\frac{1}{a} + \frac{1}{b} + \frac{1}{c})$

$\Leftrightarrow \frac{a}{b c} + \frac{b}{a c} + \frac{c}{a b} = \frac{1}{a} + \frac{1}{b} + \frac{1}{c}$

$\Leftrightarrow \frac{a^{2} + b^{2} + c^{2}}{a b c} = \frac{b c + a c + a b}{a b c}$

⇔ a² + b² + c2 = bc + ac + ab

⇔ 2a² + 2b² + 2c² = 2bc + 2ac + 2ab

⇔ (a² – 2ab + b²) + (a² – 2ac + c²) + (b² – 2bc + c²) = 0

⇔ (a – b)² + (a – c)² + (b – c)² = 0

$\Leftrightarrow \{\begin{cases} a - b = 0 \\ a - c = 0 \\ b - c = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = b \\ a = c \\ b = c \end{cases}$

⇔ a = b = c.

Vậy ∆ABC là tam giác đều.

Do đó ta chọn phương án B.

Câu 4. Cho ∆ABC biết $\frac{\cos^{2} A + \cos^{2} B}{\sin^{2} A + \sin^{2} B} = \frac{1}{2} (\cot^{2} A + \cot^{2} B)$ . Khi đó ∆ABC là:

A. Tam giác cân;

B. Tam giác thường;

C. Tam giác đều;

D. Tam giác vuông.

Hướng dẫn giải

Đáp án: A

Giải thích:

Ta có $\frac{\cos^{2} A + \cos^{2} B}{\sin^{2} A + \sin^{2} B} = \frac{1}{2} (\cot^{2} A + \cot^{2} B)$ .

$\Leftrightarrow \frac{\cos^{2} A + \cos^{2} B}{\sin^{2} A + \sin^{2} B} + 1 = \frac{1}{2} (1 + \cot^{2} A + 1 + \cot^{2} B)$

$\Leftrightarrow \frac{\cos^{2} A + \cos^{2} B + \sin^{2} A + \sin^{2} B}{\sin^{2} A + \sin^{2} B} = \frac{1}{2} (\frac{1}{\sin^{2} A} + \frac{1}{\sin^{2} B})$

$\Leftrightarrow \frac{2}{\sin^{2} A + \sin^{2} B} = \frac{1}{2} . \frac{\sin^{2} A + \sin^{2} B}{\sin^{2} A . \sin^{2} B}$

(Áp dụng kết quả Bài tập 5a và 5d, trang 65, Sách giáo khoa, Toán 10, Tập một).

⇔ (sin²A + sin²B)2 = 4.sin²A.sin²B

⇔ sin⁴A + 2.sin²A.sin²B + sin⁴B – 4.sin²A.sin²B = 0

⇔ sin⁴A – 2.sin²A.sin²B + sin⁴B = 0

⇔ (sin²A – sin²B)² = 0

⇔ sin²A = sin²B

Theo hệ quả định lí sin, ta được ${(\frac{a}{2 R})}^{2} = {(\frac{b}{2 R})}^{2}$

$\Leftrightarrow \frac{a^{2}}{{(2 R)}^{2}} = \frac{b^{2}}{{(2 R)}^{2}}$

⇔ a² = b²

⇔ a = b hay BC = AC.

Vậy ∆ABC cân tại C.

Do đó ta chọn phương án A.

Câu 5. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C.

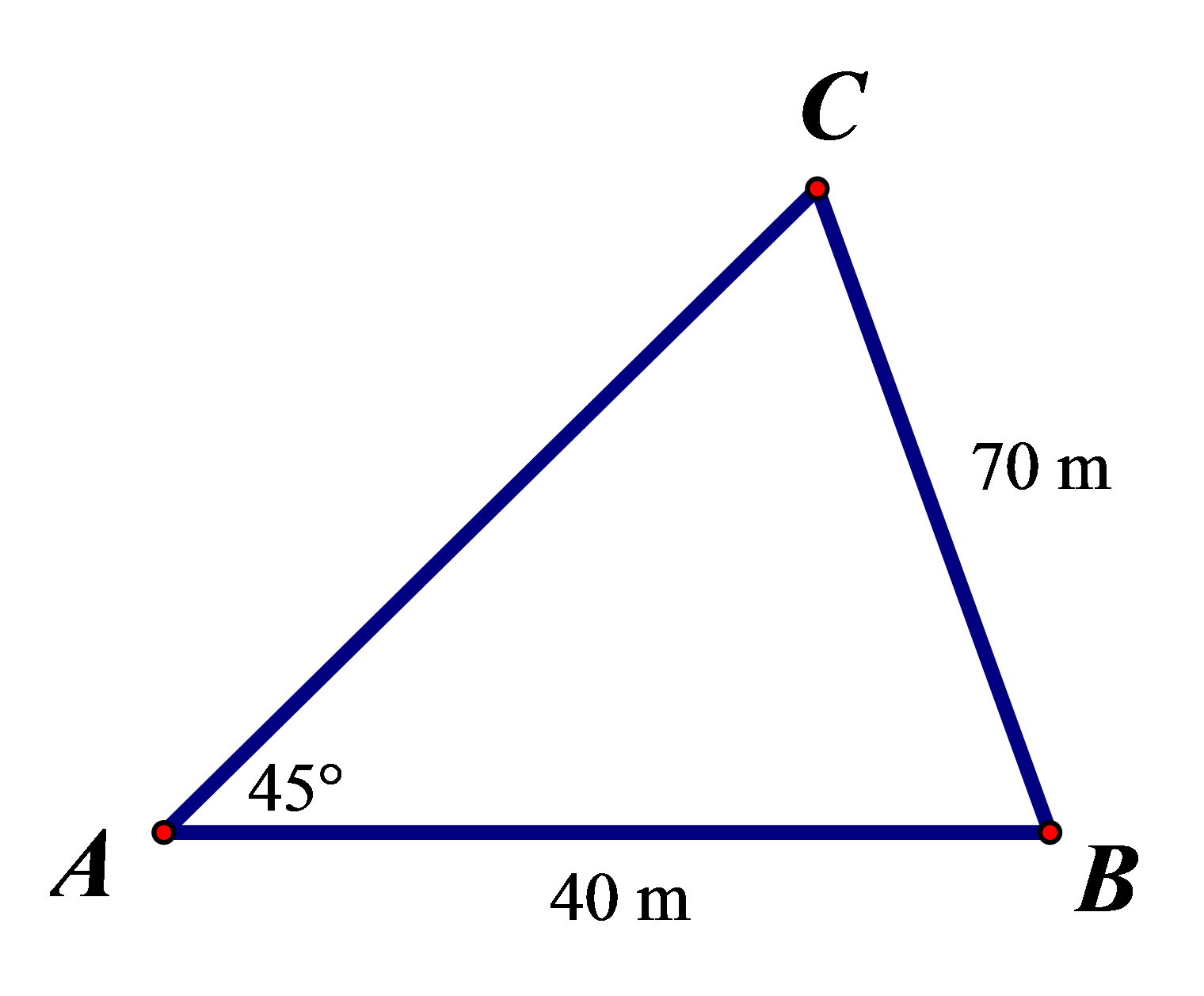
TOP 20 câu Bài tập Giải tam giác và ứng dụng thực tế - Toán 10 Chân trời sáng tạo (ảnh 1)

Người ta đo được khoảng cách AB = 40 m, BC = 70 m, $\hat{C A B} = 45 °$ . Vậy sau khi đo đạc và tính toán, ta được khoảng cách AC gần nhất với giá trị nào sau đây?

A. 35,7 m;

B. 30,6 m;

C. 92,3 m;

D. 41,5 m.

Hướng dẫn giải

Đáp án: C

Giải thích:

Áp dụng định lí côsin cho ∆ABC, ta được:

BC² = AB² + AC² – 2.AB.AC.cosA

Suy ra 70² = 40² + AC² – 2.40.AC.cos45°

Do đó $A C^{2} - 40 \sqrt{2} . A C - 3300 = 0$

Vì vậy $A C = 10 \sqrt{41} + 20 \sqrt{2}$ hoặc $A C = - 10 \sqrt{41} + 20 \sqrt{2}$ .

Vì AC > 0 nên ta nhận $A C = 10 \sqrt{41} + 20 \sqrt{2}$ ≈ 92,3 (m)

Do đó ta chọn phương án C.

Xem thêm các bài trắc nghiệm Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Bài 2: Bài tập Định lí côsin và định lí sin

Trắc nghiệm Bài 3: Giải tam giác và ứng dụng thực tế

Trắc nghiệm Ôn tập chương 4

Trắc nghiệm Toán 10 Bài 1: Khái niệm vectơ

Trắc nghiệm Toán 10 Bài 2: Tổng và hiệu của hai vectơ

Bài liên quan:

Leave a Comment Hủy