Lý thuyết Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9
Video giải Toán 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9 – Cánh diều
A. Lý thuyết Dấu hiệu chia hết cho 3, cho 9
I. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
Ví dụ:
+ Số 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 thì số 102 chia hết cho 3.
+ Số 321 có tổng các chữ số là 3 + 2 + 1 = 6 chia hết cho 3 thì số 321 chia hết cho 3.
II. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Ví dụ:
+ Số 792 có tổng các chữ số là 7 + 9 + 2 = 18 chia hết cho 9 thì số 792 chia hết cho 9.
+ Số 108 có tổng các chữ số là 1 + 0 + 8 = 9 chia hết cho 9 thì số 108 chia hết cho 9.
B. Bài tập tự luyện
Bài 1. Cho các số 104, 627, 3 114, 5 123, 6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Lời giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Bài 2. Chứng minh rằng tích của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
Lời giải:
Gọi 3 số tự nhiên liên tiếp là n; n + 1; n + 2 (với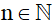 )
)
Tích của ba số tự nhiên liên tiếp là n(n + 1)(n + 2)
Mọi số tự nhiên n khi chia cho 3 có thể nhận số dư là 0, 1, 2.
+ Nếu r = 0 thì n chia hết cho 3. Khi đó n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 1 thì n có dạng n = 3k + 1 (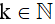 )
)
Ta có: n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 2 thì n có dạng n = 3k + 2 (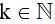 )
)
Khi đó: n + 1 = 3k + 2 + 1 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
Vậy tích của ba số tự nhiên liên tiếp chia hết cho 3.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 8: Dấu hiệu chia hết cho 2, cho 5
Lý thuyết Bài 9: Dấu hiệu chia hết cho 3, cho 9
Lý thuyết Bài 10: Số nguyên tố. Hợp số
Lý thuyết Bài 11: Phân tích một số ra thừa số nguyên tố
Lý thuyết Bài 12: Ước chung và ước chung lớn nhất