Bộ 20 Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – 2024

By 0

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 6 Kết nối tri  bản word có lời giải chi tiết:

B1:   –

B2:   – nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu 

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Kết nối tri thức

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 1

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

A. Phần đề bài

I. Trắc nghiệm (3 điểm)

Câu 1. Trong các số dưới đây, số nào là số nguyên tố?

A. 1 

B. 57

C. 39

D. 97

Câu 2. Cho tập hợp A = {x ∈ N|17 ≤ x ≤ 20} . Tổng các phần tử của tập hợp A là:

A. 74

B. 37

C. 54

D. 44

Câu 3. Thứ tự thực hiện phép tính nào sau đây là đúng?

A. Lũy thừa – Cộng, trừ – nhân, chia.

B. Cộng, trừ – nhân, chia – Lũy thừa.

C. Cộng, trừ – lũy thừa – nhân, chia.

D. Lũy thừa – Nhân, chia – cộng, trừ.

Câu 4. Số mũ của kết quả của phép tính sau: 512 . 59 : 125

A. 518

B. 18

C. 17

D. 517

Câu 5. Các phát biểu sau đúng hay sai. Đánh dấu X vào ô được lựa chọn

Các phát biểu

Đúng

Sai

1. Số 0 là hợp số

    

2. 15 chia hết cho 3 và chia hết cho 9

    

3. Số nguyên biểu diễn cho số La Mã XVI là 16

    

4. Số chục của số 712 là 12.

    

II. Tự luận (7 điểm)
 Bài 1. (2 điểm) Thực hiện phép tính:

a) 37.89 + 37.11;

b) 24 – 2.32;

c) 250:{5.[88.78970 – (2 024 – 1 946)]};

d) 3.103 + 2.102 + 0.10 + 5.

Bài 2. (2 điểm) Tìm số tự nhiên x, biết: 

a) x + (120 – 25) = 345;

b) 16.x = 42.43;

c) 15.(x + 1) + 35 = 2.102;

d) x ∈ BC và x < 200.

Bài 3. (2 điểm) Bạn Hoa muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông sao cho tấm bìa được cắt hết, không thừa không thiếu. Tính độ dài lớn nhất của cạnh hình vuông.

Bài 4. (0,5 điểm) Kết quả của phép tính: 2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029.

Bài 5. (0,5 điểm) Cho A = 1 + 3 + 32 + 33 + … + 3101. Chứng minh rằng A chia hết cho 13

Tập làm văn lớp 5: Tả cảnh sân trường giờ ra chơi (Dàn ý + 20 Mẫu) - Tin Tức Giáo Dục Học Tập Tiny

B. Đán án và lời giải  

I. Phần trắc nghiệm

Câu 1: D

Câu 2: C

Câu 3: D

Câu 4: B

Câu 1:

Số 1 chỉ có một ước là chính nó nên 1 không phải số nguyên tố.

Số 57 có tổng các chữ số là 5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3. Do đó 57 có một ước khác ngoài 1 và chính nó nên 57 là hợp số.

Số 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3 nên 39 chia hết cho 3. Do đó 39 có một ước khác ngoài 1 và chính nó nên 39 là hợp số.

Số 97 chỉ có hai ước là 1 và chính nó nên 97 là số nguyên tố.

Chọn D

Câu 2:

Các số tự nhiên lớn hơn hoặc bằng 17 và nhỏ hơn 20 gồm: 17; 18; 19.

⇒ A ={17; 18; 19}

Khi đó tổng các phần tử của tập hợp A là: 17 + 18 + 19 = 54.

Chọn C.

Câu 3:

Thứ tự thực hiện phép tính:

Lũy thừa – Nhân, chia – cộng, trừ.

Chọn D.

Câu 4:

512 . 59 : 125 = 512+9 : 53 = 521 : 53 = 521 – 3 = 518

Vậy số mũ của kết quả của phép tính là: 18.

Chọn B

Câu 5:

Số 0 không phải là hợp số nên phát biểu 1) sai.

15 có tổng các chữ số là 1 + 5 = 6 chia hết cho 3 nhưng không chia hết cho 9 nên 15 chia hết cho 3, không chia hết cho 9. Do đó 2) sai.

Số nguyên biểu diễn cho số La Mã XVI là 16. Do đó 3) đúng.

Số chục của số 712 là: 710. Do đó 4) sai.

Ta có bảng sau: 

Các phát biểu

Đúng

Sai

1. Số 0 là hợp số

  

X

2. 15 chia hết cho 3 và chia hết cho 9

  

X

3. Số nguyên biểu diễn cho số La Mã XVI là 16

X

  

4. Số chục của số 712 là 12.

  

X

 II. Phần tự luận

Câu 1:

 a) 37.89 + 37.11

= 37.(89 + 11)

= 37.100

= 3 700.

b) 34 – 2.32

= 81 – 2.9

= 81 – 18 

= 63.

c) 250:{5.[88.78970 – (2 024 – 1 946)]}

= 250:{5.[88.1 – 78]}

= 250:{5.10}

= 250:50

= 5.

d) 3.103 + 2.102 + 0.10 + 5

= 3.1 000 + 2.100 + 0.10 + 5

= 3 205 (Theo cấu tạo số).

Câu 2:

a) x + (120 – 25) = 345 

x + 95 = 345

x         = 345 – 95

x         = 250.

Vậy x = 250.

b) 16.x = 42.43

16.x = 42 + 3

16x = 45

x = 45 : 16

x = 45 : 42

x = 45 – 2 

x = 43

x = 64.

Vậy x = 64.

c) 15.(x + 1) + 35 = 2.102

15(x + 1) + 35 = 200

15(x + 1) = 200 – 35

15(x + 1) = 165

x + 1 = 165:15

x + 1 = 11

x = 11 – 1

x = 10.

Vậy x = 10.

d) Vì 45 = 15.3 nên 45 chia hết cho 15.

Do đó BCNN(15, 45) = 45.

⇒ BC(15;45) = B(45) = {0; 45; 90; 135; 180; 225; …}

⇒ x ∈ {0; 45; 90; 135; 180; 225; …}

Mà x < 200 nên x ∈ {0; 45; 90; 135; 180}.

Vậy x ∈ {0; 45; 90; 135; 180}

Câu 3:

Gọi x là độ dài lớn nhất của cạnh hình vuông 

Vì ta cắt tấm bìa hình chữ nhật có kích thước 60cm, 96cm thành các hình vuông sao cho tấm bìa được cắt hết và không thừa không thiếu nên độ dài cạnh của hình vuông là ước của 60 và 96. Hơn nữa x là lớn nhất nên x chính là ƯCLN(60,96).

Ta có: 60 = 22.3.5, 96 = 25.3

ƯCLN(60,96) = 22.3 = 12.

 x = 12 cm.

Vậy độ dài lớn nhất của hình vuông có thể cắt được là 12cm.

Câu 4:

2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029

= (2 021 + 2 029) + (2 022 + 2 028) + (2 023 + 2 027) + (2 024 + 2 026) + 2 025

= 4 050 + 4 050 + 4 050 + 4 050 + 2 025

= 16 200 + 2 025

= 18 225.

Câu 5:

Số các số hạng là: 101 – 0 + 1 = 102 số.

Ta nhận thấy:

1 + 3 + 32 = 1 + 3 + 9 = 13;

33 + 34 + 35 = 33(1 + 3 + 32) = 33.13;

…

Mà 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 nên 102 chia hết cho 3, nghĩa là:

A = (1 + 3 + 32) + (33 + 34 + 35) + … + (399 + 3100 + 3101)

= (1 + 3 + 32) + 33(1 + 3 + 32) + … + 399(1 + 3 + 32)

= 13 + 33.13 + … + 399.13

= 13.(1 + 33 + … + 399) chia hết cho 13.

Vậy A chia hết cho 13.

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 2

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

A. Phần đề bài

I. Trắc nghiệm (2 điểm)

Câu 1. Không làm phép tính hãy cho biết tổng nào sau đây chia hết cho 5?

A. 80 + 1 945 + 15.

B. 1 930 + 100 + 21.

C. 34 + 105 + 20.

D. 1 025 + 2 125 + 46.

Câu 2. Tính 14 + 2.82.

A. 142;                 B. 143;                 C. 144;                 D. 145

Câu 3. Phát biểu dưới đây là sai?

A. 6 là ước của 12.

B. 35 + 14 chia hết cho 7.

C. 121 là bội của 12.

D. 219. 26 + 13 chia hết cho 13.

Câu 4: Số La Mã biểu diễn số 29 là?

A. XIX;

B. XXIX;

C. XXXI;

D. XXVIV

II. Tự luận (7 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 120 + [55 – (11 – 3.2)2] + 23;

b) 23.3 – (110 + 15) : 42;

c) 21.[(1 245 + 987):23 – 15.12] + 21;

d) 321 – 21.[(2.33 + 44:32) – 52].

Bài 2. (2 điểm) Tìm giá trị của x thỏa mãn: 

a) 3(5x – 15) – 52 = 68;

b) {23 + [1 + (3 – 1)2]}:x = 13;

c) 32 < 2x ≤ 512;

d) Thay x trong số [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Kết nối tri thức (3 đề)   bằng chữ số thích hợp để số đó chia hết cho 9.

Bài 3. (2 điểm) Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.

Bài 4. (1 điểm) Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.

Bài 5. (1 điểm) Gọi A = n2 + n + 1 (với n ∈ N). Chứng tỏ rằng A không chia hết cho 4.

B. Phần đáp án và lời giải

Phần I. Trắc nghiệm

Bảng đáp án (0,5 × 4 = 2 điểm)

Câu 1: A

Câu 2: A

Câu 3: C

Câu 4: B

Hướng dẫn chi tiết:

Câu 1:

Ta có:

+) Vì 80 ⋮5; 1 945 ⋮ 5; 15 ⋮ 5 nên 80 + 1 945 + 15 ⋮ 5. Do đó A đúng.

+) Vì 1 930 ⋮ 5; 100 ⋮ 5 và 21 ⋮ 5 nên 1 930 + 100 + 21 không chia hết cho 5. Do đó B sai.

+) Vì 105 ⋮ 5; 20  ⋮ 5 và 34 ⋮ 5 nên 34 + 105 + 20 không chia hết cho 5. Do đó C sai.

+) Vì 1 025 ⋮ 5; 2 125 ⋮ 5 và 46 ⋮ 5 nên 1 025 + 2 125 + 46 không chia hết cho 5. Do đó D sai.

Chọn A.

Câu 2:

14 + 2.82 = 14 + 2.64 = 14 + 128 = 142.

Chọn A. 

Câu 3:

Ta có 12 chia hết cho 6 nên 6 là ước của 12. Do đó A đúng.

Vì 35 chia hết cho 7 và 14 chia hết cho 7 nên 35 + 14 chia hết cho 7. Do đó B đúng.

121 không chia hết cho 12 nên 121 không là bội của 12. Do đó C sai.

Ta có 219.26 = 219.13.2 chia hết cho 13, 13 cũng chia hết cho 13 nên 219.26 + 13 chia hết cho 13. Do đó D đúng.

Chọn C.

Câu 4:

Số La Mã biểu diễn cho số 29 là: XXIX.

Chọn B.

Phần II. Tự luận

Câu 1:

a) 120 + [55 – (11 – 3.2)2] + 23

= 120 + [55 – (11 – 6)2] + 8

= 120 + [55 – 52] + 8

= 120 + [55 – 25] + 8

= 120 + 30 + 8 

= 150 + 8 

= 158.

b) 23.3 – (110 + 15) : 42

= 8.3 – (1 + 15) : 16

= 24 – 16 : 16

= 24 – 1 

= 23.

c) 21.[(1 245 + 987):23 – 15.12] + 21

= 21.[2 232:8 – 180] + 21

= 21.[279 – 180] + 21

= 21.99 + 21

= 21(99 + 1)

= 21.100

= 2 100.

d) 321 – 21.[(2.33 + 44:32) – 52].

= 321 – 21[2.27 + 64:32) – 52]

= 321 – 21[54 + 2 – 52]

= 321 – 21.4

= 321 – 84 

= 237.

Câu 2:

a) 3(5x – 15) – 52 = 68

3(5x – 15) = 68 + 52

3(5x – 15) = 120

5x – 15 = 120:3

5x – 15 = 40

5x = 40 + 15

5x = 55

x = 55:5

x = 11.

Vậy x = 11.

b) {23 + [1 + (3 – 1)2]}:x = 13

{8 + [1 + 22]}:x = 13

{8 + [1 + 4]}:x = 13

{8 + 5}:x = 13

13:x = 13

x = 13:13

x = 1.

Vậy x = 1. 

c) Ta có: 32 < 2x ≤ 512

Mà 32 = 2.2.2.2.2 = 25; 512 = 2.2.2.2.2.2.2.2.2 = 29.

Nghĩa là 25 < 2x ≤ 29.

Khi đó: 5 < x ≤ 9, mà x là số tự nhiên nên x ∈ {6; 7; 8; 9}.

Vậy x ∈ {6; 7; 8; 9}.

d) Ta có 2 + 3 + x + 5 = 10 + x.

Để số đã cho chia hết cho 9 thì 10 + x phải chia hết cho 9.

Nên x thuộc {8; 17; 26; …}.

Mà x là chữ số nên x = 8.

Vậy x = 8.

Câu 3:

Gọi số người tham gia buổi tập đồng diễn thể dục là x (x ∈ N, 400 < x < 500).

Do số người tham gia xếp thàng hàng 5, hàng 6 và hàng 8 đều thừa một người nên ta có:

x – 1 5

x – 16

x – 18

nên x – 1 ∈ BC(5, 6, 8).

Ta có 5 = 5, 6 = 2.3, 8 = 23.

Khi đó: BCNN(5, 6, 8) = 23.3.5 = 8.3.5 = 120.

Suy ra BC(5, 6, 8) = B(120) = {0; 120; 240; 360; 480; 600; …}.

Do đó x – 1 ∈ {0; 120; 240; 360; 480; 600; …}.

Hay x ∈ {1; 121; 241; 361; 481; 601; …}.

Mà 400 < x < 500 nên x = 481. 

Câu 4:

Gọi số chia và thương lần lượt là b và q (b; q ∈ N, b ≠0).

Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).

Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1

Mà b > 12 nên b = 77 và q = 1.

Do đó 89 : 77 = 1 (dư 12).

Vậy số chia bằng 77, thương bằng 1.

Câu 5:

Ta có: A = n2 + n + 1 = n(n+1)+1

Vì n ∈ N nên n + 1 ∈ N. 

Nếu n là số chẵn thì n(n + 1) chia hết cho 2.

Nếu n là số lẻ thì n + 1 là số chẵn nên n(n + 1) chia hết cho 2.

Do đó n(n + 1) chia hết cho 2 với mọi số tự nhiên n.

Mà 1 không chia hết cho 2 nên n(n+1) + 1 không chia hết cho 2.

Suy ra n(n + 1) + 1 không chia hết cho 2 với mọi số tự nhiên n.

Vậy A không chia hết cho 4 với mọi số tự nhiên n.

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 3

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

A. Phần đề bài

I. Trắc nghiệm (2 điểm)

Câu 1. Cho tập hợp A = {chó, mèo, lợn, gà}. Phát biểu nào dưới đây là đúng?

A. Chó ∈ A;

B. Mèo ∉ A;

C. Cá ∈ A;

D. Lợn ∉ A.

Câu 2. Chữ số 2 trong số 123 857 có giá trị là:

A. 120 000

B. 20 000

C. 23 857

D. 20

Câu 3. Trong các số sau: 114, 76; 1 029; 354; 57. Có bao nhiêu số chia hết cho 3?

A. 3

B. 0

C. 5

D. 4

Câu 4. Kết quả của phép tính sau: 78 : 7

A. 78;

B. 76;

C. 77;

D. 79.

II. Tự luận (8 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 12 + 3.25 : 4 – 3;

b) 120 + [55 – (11 – 3.2)2] + 23;

c) 240.14.83 + 7.2.17.

Bài 2. (2 điểm) Tìm x, biết:

a) 2x + 15 = 242:2;

b) (3x – 4)3 = 125;

c) x ∈ ƯC(18,54) và x > 6.

Bài 3. (1 điểm) Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2 và 5, lớn hơn 12 nhỏ hơn hoặc bằng 70. Hãy viết tập hợp A theo hai cách.

Bài 4. (1,5 điểm) Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?

Bài 5. (0,5 điểm) Tìm số tự nhiên có hai chữ số biết số đó chia cho tổng các chữ số của nó thu được 7 dư 6.

Tả cảnh sân trường em vào giờ ra chơi - Thư viện bài tập

B. Đáp án và hướng dẫn giải

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 4 = 2 điểm)

Câu 1: A

Câu 2: B

Câu 3: D

Câu 4: C

 

Hướng dẫn chi tiết

Câu 1:

Ta có:

Chó là một phần tử của tập hợp A nên ta viết chó ∈ A. Do đó A đúng.

Mèo là một phần tử của tập hợp A nên ta viết mèo ∈ A. Do đó B sai.

Cá không phải là phần tử của tập hợp A nên ta viết cá ∉ A. Do đó C sai.

Lợn là một phần tử của tập hợp A nên ta viết lợn ∈ A. Do đó D sai.

Chọn A.

Câu 2:

Trong số 123 857, chữ số 2 là chữ số hàng chục nghìn nên chữ số 2 có giá trị 2.10 000 = 20 000.

Chọn B.

Câu 3:

Ta có:

1 + 1 + 4 = 6 chia hết cho 3 nên 114 chia hết cho 3;

7 + 6 = 13 không chia hết cho 3 nên 76 không chia hết cho 3;

1 + 0 + 2 + 9 = 12 chia hết cho 3 nên 1 029 chia hết cho 3;

3 + 5 + 4 = 12 chia hết cho 3 nên 354 chia hết cho 3;

5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3.

Vậy có 4 số chia hết cho 3.

Chọn D

Câu 4:

Ta có: 78 : 7 = 78 – 1 = 77.

Chọn C.

II. Tự luận

Bài 1:

a) 12 + 3.25 : 4 – 3

= 12 + 3.32:4 – 3

= 12 + 3.8 – 4

= 12 + 24 – 4

= 36 – 4

= 32

b) 120 + [55 – (11 – 3.2)2] + 23

= 120 + [55 – (11 – 6)2] + 8

= 120 + [55 – 42] + 8

= 120 + [55 – 16] + 8

= 120 + 39 + 8

= 159 + 8

= 167

c) 240.14.83 + 7.2.17

= 14.83 + 14.17

= 14.(83 + 17)

= 14.100

= 1 400.

Bài 2:

a) 2x + 15 = 242:2

2x + 15 = 121

2x = 121 – 15

2x = 106

x = 106 : 2

x = 53.

Vậy x = 53.

b) (3x – 4)3 = 125

(3x – 4)3 = 53

3x – 4 = 5

3x = 5 + 4

3x = 9

x = 9:3

x = 3.

Vậy x = 3.

c) x ƯC(18,54) và x > 6

Ta có: 18 = 2.32, 54 = 2.33

Khi đó: ƯCLN(18, 54) = 2.32 = 18.

ƯC(18,54) = Ư(18) = {1; 2; 3; 6; 9; 18}

x ∈ {1; 2; 3; 6; 9; 18}

Mà x > 6 nên x ∈ {9; 18}.

Vậy x ∈ {9; 18}.

Bài 3:

Các số tự nhiên chia hết cho 2 và cho 5 là các số tự nhiên có chữ số tận cùng bằng 0: 0; 10; 20; 30; 40; 50; 60; 70; 80; …

Các số tự nhiên ở trên thỏa mãn lớn hơn 12 nhỏ hơn hoặc bằng 70 là: 20; 30; 40; 50; 60; 70.

Theo cách liệt kê, tập hợp A được mô tả: A = {20; 30; 40; 50; 60; 70}.

Theo cách chỉ ra tính chất đặc trưng, ta viết: {x ∈ N|x2, x5, 12 < x ≤ 70}

Bài 4:

Gọi số bút trong mỗi hộp bút chì màu là x ( x ∈ N, x > 2) (chiếc).

Vì số bút trong mỗi hộp là như nhau nên 25 và 20 chia hết cho x hay x ƯC(25, 20).

Ta có: 25 = 52, 20 = 22.5;

ƯCLN(25, 20) = 5.

ƯC(25, 20) = Ư(5) = {1; 5}

x ∈ {1; 5}

Mà x > 2 nên x = 5 (thỏa mãn điều kiện).

Vậy trong mỗi hộp có 5 chiếc bút.

Bài 5:

Gọi số tự nhiên có hai chữ số cần tìm là  (Với a,b {0;1;2;3; …; 9} và a ≠ 0 )

Ta có tổng các chữ số của nó là: a + b.

Vì số dư phép chia là 6 nên a + b > 6.

Theo đầu bài ta có: [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Kết nối tri thức (3 đề)   = 7(a + b) + 6

10a + b = 7a + 7b + 6

3a = 6b + 6

a = 2b + 2

a = 2(b + 1)

Mà 0 < a ≤ 9 ⇔ 0 < 2(b + 1) ≤ 9 ⇒ 0 < b + 1 < 4,5.

Do đó 0 ≤ b < 5.

Ta có bảng sau:

b

a = 2(b + 1)

a + b (a + b > 6)

0

2

3 (loại)

1

4

5 (loại)

2

6

8 (thỏa mãn)

3

8

11 (thỏa mãn)

4

10 (loại)

  

 Vậy số cần tìm là 62 và 83.

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 4

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

I. TRẮC NGHIỆM: (3,0 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng trong mỗi câu sau:

Câu 1. Cho tập hợp A = {a; b; c; d}, khẳng định nào sau đây là đúng?

A. c ∈ A
B. d ∈ A
C. e ∈ A
D. a ∉ A

Câu 2. Tập hợp nào sau đây chỉ gồm các phần tử là số tự nhiên?

A. \left\{\frac{3}{5};2\right\}
B. {1; 2; 3}
C. \left\{2\frac{1}{3};5\right\}
D. {0; 2; 4}

Câu 3. Với a, m, n là các số tự nhiên, khẳng định nào sau đây đúng?

A. am . an = am + n (a ≠ 0)
B. am . an = am.n (a ≠ 0)
C. am : an = am.n (a ≠ 0)
D. am : an = m – n (a ≠ 0)

Câu 4. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc là:

A. Lũy thừa → Nhân, chia → Cộng, trừ.
B. Nhân chia → Cộng trừ → Lũy thừa.
C. Nhân chia → Lũy thừa → Cộng, trừ.
D. Cộng, trừ → Nhân, chia → Lũy thừa.

Câu 5. Kết quả của phép tính 23. 22 là:

A. 45
B. 25
C. 26
D. 46

Câu 6. Số tự nhiên nào sau đây chia cho 5 dư 2?

A. 4
B. 5
C. 6
D. 7

Câu 7. Số tự nhiên nào sau đây chia hết cho cả 2 và 5?

A. 126
B. 259
C. 430
D. 305

Câu 8. Trong các số tự nhiên sau, số nào là số nguyên tố?

A. 4
B. 7
C. 18
D. 25

Câu 9. Số tự nhiên nào sau đây là ước của 10?

A. 0
B. 3
C. 2
D. 11

Câu 10. Số tự nhiên nào sau đây là BCNN(4, 6)?

A. 15
B. 12
C. 10
D. 9

Câu 11. Khi mô tả các yếu tố của hình vuông, khẳng định nào sau đây sai:

A. Hình vuông có 4 cạnh bằng nhau;
B. Hình vuông có 4 góc vuông;
C. Hình vuông có các cạnh đối không bằng nhau;
D. Hình vuông có hai đường chéo bằng nhau.

Câu 12. Hình nào sau đây là hình chữ nhật?

Câu 12

II. TỰ LUẬN: (7,0 điểm)

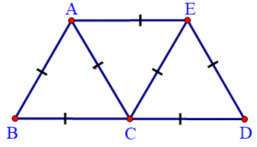
Câu 1. (1,0 điểm) Trong hình vẽ bên có bao nhiêu tam giác đều? Hãy viết tên các tam giác đều đó.

Câu 1

Câu 2. (2,0 điểm)

a) Viết tập hợp A các số tự nhiên không vượt quá 7.

b) Viết các số 23 và 29 bằng số La Mã.

Câu 3. (1,5 điểm)

a) Thực hiện phép tính: ( tính hợp lý nếu có thể) 12. 35 + 12. 65

b) Tìm x, biết: (123 – 4x) – 67 = 23

Câu 4. (1,5 điểm)

a) Tìm tập hợp BC (30; 45)

b) Một đội y tế có 24 bác sĩ và 108 y tá. Có thế chia đội y tế đó nhiều nhất thành mấy tổ để số y tá được chia đều vào các tổ ?

Câu 5. (1,0 điểm) Tìm n ∈ N biết để 3 chia hết cho n + 2.

Đáp án đề thi giữa kì 1 môn Toán 6 năm 2022 – 2023

I. TRẮC NGHIỆM (3,0 điểm) Mỗi câu trả lời đúng: 0,25 điểm

Câu 1

Câu 2

Câu 3

Câu 4

Câu 5

Câu 6

Câu 7

Câu 8

Câu 9

Câu 10

Câu 11

Câu 12

B

D

A

A

B

D

C

B

C

B

C

A

II. TỰ LUẬN ( 7,0 điểm)

Câu

Nội dung

Điểm

1

Có ba tam giác đều đó là: ABC; ACE; CED .

1,0

2

a) Tập hợp A các số tự nhiên không vượt quá 7 là:

A = {0; 1; 2; 3; 4; 5; 6; 7}

0,5

b) XIII, XXIX

0,5

3

a) 12. 35 + 12. 65

= 12. (35 + 65)

= 12. 100

= 1200

 

0,25

 

0,25

b) (123 – 4x) – 67 = 23

(123 – 4x) – 67 = 8

123 – 4x = 8 + 67

123 – 4x = 75

4x = 123 – 75

4x = 48

x = 48: 4

x = 12

Vậy x = 12

 

0,25

 

0,25

 

0,25

 

0,25

4

a) 30 = 2.3.5

45 = 32.5

BCNN (30,45) = 2.32.5 = 90

BC(30,45) = {0; 90; 180;270;…}

0,25

 

0,25

 

b) Gọi số tổ là a (a ∈ N*)

Theo bài ra 24 bác sĩ và 108 y tá được chia đều vào các tổ nên ta có:

24 \vdots a

108 \vdots a

⇒ a ∈ ƯC (108; 24)

Mà số tổ được chia là nhiều nhất nên a = ƯCLN(108; 24)

Ta có: 24 = 23.3

108 = 22.33

=> ƯCLN(24,108) = 22.3 = 12

=> a = 12

Vậy có thể chia đội y tế đó nhiều nhất thành 12 tổ.

0,25

 

0,25

 

 

0,25

 

 

0,25

5

Để 3 chia hết cho n + 1

⇒ (n + 1) ∈ Ư(3) = {1;3}

⇒ n ∈ {0;2}

Vậy n ∈ {0;2}

0,25

0,5

0,25

0,25

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 5

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Kết nối tri thức

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

I. Phần trắc nghiệm (4 điểm)

Câu 1: Cho tập hợp A = \left\{ {x;5;y;7} \right\}. Chọn khẳng định đúng.

A. 5 \in A

B. 0 \in A

C. 7 \notin A

D. y \notin A

Câu 2: Tập hợp B = \left\{ {0;1;2;...;100} \right\} có số phần tử là:

A. 99

B. 100

C. 101

D. 102

Câu 3: Số vừa chia hết cho 3 vừa chia hết cho 5 là:

A. 425

B. 693

C. 660

D. 256

Câu 4: Lũy thừa với số mũ tự nhiên có tính chất nào sau đây?

A. {a^m}.{a^n} = {a^{m - n}}

B. {a^m}.{a^n} = {a^{mn}}

C. {a^m}:{a^n} = {a^{m:n}}

D. {a^m}.{a^n} = {a^{m + n}}

Câu 5: Cặp số chia hết cho 2 là:

A. (234; 415)

B. (312; 450)

C. (675; 530)

D. (987; 123)

Câu 6: Tìm khẳng định đúng trong các khẳng định sau:

A. Một số chia hết cho 9 thì luôn chia hết cho 3

B. Nếu hai số chia hết cho 3 thì tổng của hai số đó chia hết cho 9

C. Mọi số chẵn thì luôn chia hết cho 5

D. Số chia hết cho 2 là số có chữ số tận cùng bằng 0; 2; 3; 4; 6; 8

Câu 7: Số 41 là

A. hợp số

B. không phải số nguyên tố

C. Số nguyên tố

D. không phải hợp số

Câu 8: Các cặp số nào sau đây nguyên tố cùng nhau?

A. 3 và 11

B. 4 và 6

C. 2 và 6

D. 9 và 12

II. Phần tự luận (6 điểm)

Câu 1: Thực hiện các phép tính:

a. 667 - 195.93:465 + 372

b. {35^0}.12.173 + 12.27

c. {73.5^2} + {5^2}.28 - {5^2}

d. 321 - 21.\left[ {\left( {{{2.3}^3} + {4^4}:32} \right) - 52} \right]

Câu 2: Tìm x biết:

a. 2x + 15 = 142:2

b. {5^3}:x + 100 = 125

c. 3.\left( {5x - 15} \right) - 52 = 68

d. 35 \vdots x;130 \vdots x và x lớn nhất

Câu 3: Một đội y tế có 280 nam, 220 nữ dự định chia thành các nhóm sao cho số nam và số nữ ở mỗi nhóm đều nhau, biết số nhóm chia được nhiều hơn 1 nhóm và không lớn hơn 5 nhóm. Hỏi có thể chia đội thành mấy nhóm? Khi đó mỗi nhóm có bao nhiêu nam, bao nhiêu nữ?

Câu 4: Cho A = 1 + 3 + {3^2} + {3^3} + ... + {3^{101}}. Chứng minh rằng A chia hết cho 13

Đáp án Đề thi Toán lớp 6 giữa học kì 1

I. Phần trắc nghiệm (4 điểm)

1. A

2. C

3. C

4. D

5. B

6. A

7. C

8. A

II. Phần tự luận (6 điểm)

Câu 1:

a. 667 - 195.93:465 + 372 = 667 - 39 + 372 = 1000

b. {35^0}.12.173 + 12.27 = 1.12.173 + 12.27 = 12\left( {173 + 27} \right) = 12.200 = 2400

c. {73.5^2} + {5^2}.28 - {5^2} = {5^2}\left( {73 + 28 - 1} \right) = {5^2}.100 = 25.100 = 2500

d. 321 - 21.\left[ {\left( {{{2.3}^3} + {4^4}:32} \right) - 52} \right]

\begin{matrix} = 321 - 21.\left[ {\left( {2.27 + 256:32} \right) - 52} \right] \hfill \\ = 321 - 21.\left[ {\left( {54 + 8} \right) - 52} \right] \hfill \\ = 321 - 21.\left[ {62 - 52} \right] \hfill \\ = 321 - 21.10 = 321 - 210 = 111 \hfill \\ \end{matrix}

Câu 2:

a. 2x + 15 = 142:2

\begin{matrix} \Rightarrow 2x + 15 = 71 \hfill \\ \Rightarrow 2x = 71 - 15 \hfill \\ \Rightarrow 2x = 56 \hfill \\ \Rightarrow x = 28 \hfill \\ \end{matrix}

Vậy x = 28

b. {5^3}:x + 100 = 125

\begin{matrix} \Rightarrow {5^3}:x = 125 - 100 \hfill \\ \Rightarrow 125:x = 25 \hfill \\ \Rightarrow x = 125:25 = 5 \hfill \\ \end{matrix}

Vậy x = 5

c. 3.\left( {5x - 15} \right) - 52 = 68

\begin{matrix} \Rightarrow 3.\left( {5x - 15} \right) = 68 + 52 \hfill \\ \Rightarrow 3.\left( {5x - 15} \right) = 120 \hfill \\ \Rightarrow 5x - 15 = 120:3 \hfill \\ \Rightarrow 5x - 15 = 40 \hfill \\ \Rightarrow 5x = 40 + 15 \hfill \\ \Rightarrow 5x = 55 \Rightarrow x = 11 \hfill \\ \end{matrix}

Vậy x = 11

d. Ta có: 35 \vdots x;130 \vdots x \Rightarrow x \in UC\left( {35;130} \right)

Ta lại có:

\begin{matrix} \left\{ {\begin{array}{*{20}{c}} {35 = 5.7} \\ {130 = 2.5.13} \end{array}} \right. \Rightarrow UCLN\left( {35;130} \right) = 5 \hfill \\ \Rightarrow UC\left( {35;130} \right) = U\left( 5 \right) = \left\{ {1;5} \right\} \hfill \\ \end{matrix}

Do x lớn nhất => x = 5

Câu 3:

Gọi số nhóm cần chia là x (x > 1)

Ta có: Đội y tế có 280 nam, 220 nữ dự định chia thành các nhóm sao cho số nam và số nữ ở mỗi nhóm đều nhau.

280 ⋮ x ; 220 ⋮ x. Vậy x ∈ UC (280, 220)

Ta có:

280 = 23.5. 7

220 = 22.5.11

Suy ra: UCLN (280, 220) = 22.5

UC (280, 220) = U(20) {1; 2; 4; 5; 10; 20}

Do số nhóm chia được nhiều hơn 1 nhóm và không lớn hơn 5 nhóm

x∈ {2; 4; 5}

Ta có bảng sau:

Số nhóm Số người nữ trong nhóm Số nam trong nhóm
2 110 140
4 55 70
5 44 56

Câu 4

\begin{aligned} &A=1+3+3^{2}+3^{3}+\ldots+3^{101} \\ &A=\left(1+3+3^{2}\right)+\left(3^{3}+3^{4}+3^{5}\right)+\ldots+\left(3^{99}+3^{100}+3^{101}\right) \\ &A=\left(1+3+3^{2}\right)+3^{3} \cdot\left(1+3+3^{2}\right)+\ldots+3^{99} \cdot\left(1+3+3^{2}\right) \\ &A=\left(1+3+3^{2}\right)\left(1+3^{3}+\ldots+3^{99}\right) \\ &A=13 \cdot\left(1+3^{3}+\ldots+3^{99}\right): 13 \end{aligned}

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Chân trời sáng tạo

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 1

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Chân trời sáng tạo

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

I. Phần trắc nghiệm

Câu 1: Trong các hình sau đây hình nào là hình vuông?

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình a

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình b

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình c

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình d

 

A) Hình a

B) Hình b

C) Hình c

D) Hình d

Câu 2: Phân tích số 108 ra thừa số nguyên tố ta được:

A)  22.33

B) 32.22  

C)  32.23

D) 33.23

Câu 3: Từ 35 đến 60 có bao nhiêu số nguyên tố:

A) 4 số

B) 7 số 

C) 5 số

D) 6 số

Câu 4: Kết quả của phép tính 23.3 – (110 +15) : 16 là:

A) 22

B) 23

C) 24

D) 25

Câu 5: Chọn câu sai trong các câu dưới đây

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

A) Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA

B) Sáu góc đỉnh A, B, C, D, E, G bằng nhau.

C) Ba đường chéo chính là AD, BE, CG bằng nhau

D) Các đoạn thẳng BG = CG.

Câu 6: Tìm số tự nhiên x thỏa mãn:32 + 2x + 6 = 21

A) 2

B) 5

C) 3

D) 4

Câu 7: Diện tích tam giác có chiều cao là 5cm và độ dài cạnh đáy tương ứng là 8cm là:

A) 20 cm2 

B) 15 cm2 

C) 40 cm2 

D) 25 cm2

Câu 8: Chọn câu sai trong các câu dưới đây:

Cho hình thoi ABCD 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

A) AB song song với CD và BC song song với AD.

B) AB = BC = CD= AD

C) AC và BD vuông góc với nhau

D) Bốn góc đỉnh A, B, C, D bằng nhau.

II. Phần tự luận

Bài 1: Thực hiện phép tính

a) 211 :  

b)  62.10 : {780 : [103 – (2.53 + 35.14)]}

Bài 2: Tìm x

a) 2x + 15 = 142:2

b) (x + 1) + (x + 2) + (x + 3) + … + (x + 10) = 75

Bài 3: Tính chu vi và diện tích hình chữ nhật có chiều dài là 12cm và chiều rộng là 8cm.

Bài 4: Lớp bạn Hoa cần chia 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy vào trong các túi quà mang đi tặng ở trung tâm trẻ mồ côi sao cho số bút bi, bút chì và cục tẩy ở mỗi bên đều như nhau. Tính số lượng túi quà nhiều nhất mà các bạn lớp Hoa có thể chia. Khi đó, số lượng của mỗi loại bút bi, bút chì, cục tẩy trong mỗi túi quà là bao nhiêu.

Bài 5: Cho A = 1 + 3 + 32 + 33 + … + 3101 . Chứng minh rằng A chia hết cho 13.

Cột cờ đổ sập đè trúng nam sinh lớp 7

Đáp án

I. Phần tắc nghiệm

Câu 1: Trong các hình sau đây hình nào là hình vuông?

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình a

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình b

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình c

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Hình d

A) Hình a

B) Hình b

C) Hình c

D) Hình d

Giải thích vì hình b có 4 góc vuông và 4 cạnh bằng nhau nên nó là hình vuông.

Câu 2: Phân tích số 108 ra thừa số nguyên tố ta được:

A) 22.33 

B)  22.32

C)  32.23

D) 33.23 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

Do đó 108 = 22.33

Câu 3: Từ 35 đến 60 có bao nhiêu số nguyên tố:

A) 4 số

B) 7 số 

C) 5 số

D) 6 số

Từ 35 đến 60 có các số nguyên tố là: 37; 41; 43; 47; 53; 59. Vậy có 6 số nguyên  tố nằm giữa 35 đến 60

Câu 4: Kết quả của phép tính 23. 3 – (110 + 15) : 16 là:

A) 22

B) 23

C) 24

D) 25

 23. 3 – (110 + 15) : 16

= 8.3 – (1 + 15):16

= 24 – 16:16

= 24 – 1 = 23

Câu 5: Chọn câu sai trong các câu dưới đây

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

A) Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA

B) Sáu góc đỉnh A, B, C, D, E, G bằng nhau.

C) Ba đường chéo chính là AD, BE, CG bằng nhau

D) Các đoạn thẳng BG = CG.

Vì BG không phải đường chéo chính nên không bằng CG.

Câu 6: Tìm số tự nhiên x thỏa mãn: 32 + 2x + 6 = 21 

A) 2

B) 5

C) 3

D) 4

32 + 2x + 6 = 21

9 + 2x + 6 = 21

9 + 2x = 21 – 6

9 + 2x = 15

2x = 15 – 9

2x = 6

x = 6:2

x = 3

Câu 7: Diện tích tam giác có chiều cao là 5cm và độ dài cạnh đáy tương ứng là 8cm là:

A) 20 cm2

B) 15 cm2

C) 40 cm2

D) 25 cm2

Diện tích tam giác là:

S = a.h:2 = 8.5:2 = 20 cm2

Câu 8: Chọn câu sai trong các câu dưới đây:

Cho hình thoi ABCD 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

A) AB song song với CD và BC song song với AD.

B) AB = BC = CD= AD

C) AC và BD vuông góc với nhau

D) Bốn góc đỉnh A, B, C, D bằng nhau.

Ta thấy chỉ có hai đỉnh đối diện góc mới bằng nhau.

II. Phần tự luận

Bài 1: 

a)  211 : {1026 – [(34 + 1) : 41]}

=  211 : {1026 – [(81 + 1) : 41]}

= 211 : {1026 – [82 : 41]}

= 211 :  {1026 – 2}

= 211 : 1024

= 2048:1024

= 2

b)  62.10:{780 : [103 – (2.53 + 35.14)]}

= 36.10:{780 : [103 – (2.125 + 35.14)]}

= 36.10:{780 : [1000 – (250 + 490)]}

=  36.10:{780 : [1000 – 740]}

=  36.10:{780: 260}

=  36.10:3

= 360:3

=120

Bài 2: Tìm x

a) 2x + 15 = 142:2

2x + 15 = 71

2x = 71 – 15

2x = 56

x = 56:2

x = 28

Vậy x = 28

b) (x + 1) + (x + 2) + (x + 3) + … + (x + 10) = 75

x + 1 + x + 2 + x + 3 + … + x + 10 = 75

(x + x + …+ x) + (1 + 2 + 3 +… + 10) = 75

10x + (1 + 2 + 3 + … + 10) = 75

Ta tính B = 1 + 2 + …+ 10 = (1 + 10) + (2 + 9)+ (3 + 8) + (4 + 7) + (5 + 6) 

B = 11 + 11 + 11 + 11 + 11 = 55.

Ta có: 10x + 55 = 75

10x = 75 – 55

10x = 20 

x = 20:10

x = 2

Vậy x = 2.

Bài 3:

Lời giải:

Chu vi hình chữ nhật là:

P = (a + b).2 = (12 + 8).2 = 40cm

Diện tích hình chữ nhật là

S = a.b = 12.8 = 96 cm2 

Vậy chu vi hình chữ nhật là 40cm, diện tích hình chữ nhật là 96cm2 .

Bài 4: 

Lời giải:

Gọi số túi quà lớp bạn Hoa mang tặng là x (x ∈ N*)

Vì chia đều 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy vào các túi quà nên 171 x; 63 x; 27 x hay x là ước chung của 171; 63; 27.

Vì số túi quà chia được là lớn nhất nên x là ước chung lớn nhất của 171; 63; 27.

Ta có:

171 = 3.3.19 = 32 .19

63 = 3.3.7 = 32 . 19 

27 = 3.3.3 = 33 

ƯCLN (171; 63; 27) = 32  = 9 

Vậy số túi quà nhiều nhất là 9 túi

Số bút bi trong mỗi túi quà là:

171:9 = 19 (chiếc bút bi)

Số bút chì trong mỗi túi quà là:

63:9 = 7 (chiếc bút chì)

Số cục tẩy trong mỗi túi quà là:

27:9 = 3 (cục tẩy)

Bài 5: Cho A = 1 + 3 + 32 + 33 + … + 3101 . Chứng minh rằng A chia hết cho 13.

Lời giải:

A = 1 + 3 + 32 + 33 + 34 + 35) + … + 399 + 3100 + 3101

A = (1 + 3 + 32) + (33 + 34 + 35) + … + (399 + 3100 + 3101)

A =  (1 + 3 + 32) + 33 (1 + 3 + 32)+ … + 399( 1 + 3 + 32) 

A = (1 + 3 + 32)(1 + 33 + 36 + … + 399)

A = 13. (1 + 33 + 36 + … + 399)

Vì 13 chia hết cho 13 nên 13.(1 + 33 + 36 + … + 399) chia hết cho 13 nên A chia hết cho 13 

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 2

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Chân trời sáng tạo

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

I. Phần trắc nghiệm

Câu 1: Viết tập hợp sau A = {x∈ N | 8 ≤ x ≤ 12} bằng cách liệt kê các phần tử:

A) A = {8; 9; 10; 11; 12}

B) A = {9; 10; 11; 12}

C) A = {9; 10; 11}

D) A = {9; 10; 11; 12}

Câu 2: Số tự nhiên chia cho 10 dư 5 có dạng

A) 5k + 10 (với k ∈ N)

B) 5k -10 (với k ∈ N)

C) 10k + 3 (với k ∈ N)

D) 10k + 5 (với k ∈ N)

Câu 3: Phân tích số 300 ra thừa số nguyên tố

A) 23.3.52

B) 22.3.52 

C) 2.32.52

D) 23.3.5

Câu 4: Kết quả của phép tính: 250 – 52 – (32 +12):3

A) 218

B) 268

C) 232

D) 240

Câu 5: Trong các khẳng định sau, khẳng định nào sai

A) Số đối của số -6 là số 6.

B) Số đối của số 0 là số 0.

C) Số -5 nằm bên trái số -4 nên ta nói -5 lớn hơn – 4.

D) Số 0 không phải số nguyên âm cũng không phải số nguyên dương.

Câu 6: Trong các dãy số dưới đây, dãy nào chỉ toàn là số nguyên tố.

A) 1; 3; 5; 7

B) 2; 3; 5; 7

C) 1; 2; 3; 5; 7

D) 3; 5; 7; 9

Câu 7: Cho các số nguyên sau: 0; -3; 2; 5; -4; 4; 6. Sắp xếp các số nguyên đã cho theo thứ tự tăng dần

A) -3; -4; 0; 2; 4; 5; 6

B) 0; -3; -4; 2; 4; 5; 6

C) 6; 5; 4; 2; 0; -3; -4

D) -4; -3; 0; 2; 4; 5; 6

Câu 8: Tập hợp A = {a ∈ Z | -5 < a < 2}

A) 5

B) 7

C) 6

D) 8

Câu 9: Tìm số x ∈ Z thỏa mãn: 2x + 35 = 17

A) 12

B) 9

C) 26

D) -9

Câu 10: Kết quả của phép tính: 23 – 2.(-3) + 52

A) 39

B) 25

C) 27

D) 14

II. Tự luận

Bài 1: Thực hiện phép tính

a) (4 + 32 + 6) + (10 – 32 – 2)

b) (56.35 + 56.18):53

c) 12:{400:[500 – (125 + 25.7)]}

d) 303 – 3.{[655 – (18:2 + 1). +5]}: 100

Bài 2: Tìm x ∈ Z biết:

a) 22 + (x + 3) = 52

b) 125 – 5(4 + x) = 15

c) (15 + x):3 = 315 : 312

d)  2x+1 – 2x = 32

Bài 3: Bạn Vinh có 48 viên bi đỏ, 30 viên bi xanh, 66 viên bi vàng. Vinh muốn chia đều số bi vào các túi sao cho mỗi túi đều có cả ba loại bi. Hỏi Vinh có thể chia nhiều nhất bao nhiêu túi. Khi đó mỗi túi có bao nhiêu viên bi mỗi loại.

Bài 4: Tìm các số tự nhiên x; y biết 2xy + x + 2y = 13

Đáp án

I. Phần trắc nghiệm

Câu 1: Viết tập hợp sau A = {x ∈ N | 8 ≤ x ≤ 12}  bằng cách liệt kê các phần tử:

A) A = {8; 9; 10; 11; 12}

B) A = {9; 10; 11; 12}

C) A = {9; 10; 11}

D) A = {9; 10; 11; 12}

Vì 8 ≤ x ≤ 12 nên x ∈ {8; 9; 10; 11; 12}

Chú ý: ta lấy dấu bằng ở 8 và 12

Câu 2: Số tự nhiên chia cho 10 dư 5 có dạng

A) 5k + 10 (với k ∈ N)

B) 5k -10 (với k ∈ N)

C) 10k + 3 (với k ∈ N)

D) 10k + 5 (với k ∈ N)

Vì mọi số tự nhiên chia cho 10 dư 5 đều có dạng 10k + 5 với k thuộc N.

Câu 3: Phân tích số 300 ra thừa số nguyên tố

A) 23 .3.52 

B)  22 .3.52

C)  2.32.52

D)  23 .3.5

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề) 

300 = 2.2.3.5.5 = 22.3.52

Câu 4: Kết quả của phép tính: 250 – 52 – (32 +12):3

A) 218

B) 268

C) 232

D) 240

250 – 52 – (32 +12):3

= 250 – 25 – (9 + 12):3

= 250 – 25 – 21:3

=250 – 25 – 7

= 225 – 7

= 218

Câu 5: Trong các khẳng định sau, khẳng định nào sai

A) Số đối của số -6 là số 6.

B) Số đối của số 0 là số 0.

C) Trên trục số, số -5 nằm bên trái số -4 nên ta nói -5 lớn hơn – 4.

D) Số 0 không phải số nguyên âm cũng không phải số nguyên dương.

Câu C sai vì các số trên trục số nằm bên trái sẽ bé hơn các số nằm bên phải nên -5 nằm bên trái số -4 nên -5 bé hơn -4

Câu 6: Trong các dãy số dưới đây, dãy nào chỉ toàn là số nguyên tố.

A) 1; 3; 5; 7

B) 2; 3; 5; 7

C) 1; 2; 3; 5; 7

D) 3; 5; 7; 9

Vì ở đáp án A có 1 không phải số nguyên tố, đáp án C có 1 không phải số nguyên tố, đáp án D có 9 không phải số nguyên tố. Đáp án B cả 4 số đều là số nguyên tố.

Câu 7: Cho các số nguyên sau: 0; -3; 2; 5; -4; 4; 6. Sắp xếp các số nguyên đã cho theo thứ tự tăng dần

A) -3; -4; 0; 2; 4; 5; 6

B) 0; -3; -4; 2; 4; 5; 6

C) 6; 5; 4; 2; 0; -3; -4

D) -4; -3; 0; 2; 4; 5; 6

Vì đáp án D các số được sắp xếp theo thứ tăng dần.

Câu 8: Tập hợp A = {a ∈ Z | -5 < a < 2}. Tập hợp A có bao nhiêu phần tử

A) 5

B) 7

C) 6

D) 8

Ta có: A = {a ∈ Z | -5 < a < 2}

A = {-4; -3; -2; -1; 0; 1} tập A có 6 phần tử

Câu 9: Tìm số x ∈ Z thỏa mãn: 2x + 35 = 17

A) 12

B) 9

C) 26

D) -9

Giải thích

2x = 17 – 35

2x = -18

x = -18:2

x = -9

Câu 10: Kết quả của phép tính: 23 – 2.(-3) + 52   

A) 39

B) 25

C) 27

D) 14

23 – 2.(-3) + 52

= 8 – (-6) + 25

= 8 +6 + 25

= 14 + 25

= 39.

II. Phần tự luận

Bài 1: 

a) (4 + 32 + 6) + (10 – 32 – 2)

= 4 + 32 + 6 + 10 – 32 – 2

= (4 – 2) + (32 – 32) + (10 + 6)

= 2 + 0 + 16

= 18

b) (56.35 + 56.18):53

= [56.(35 + 18)]:53

= [56.53]:53

= 2968:53

= 56

c) 12:{400:[500 – (125 + 25.7)]}

= 12:{400:[500 – (125 + 175)]}

= 12:{400:[500 – 300]}

= 12:{400:200}

=12:2 = 6

d) 303 – 3.[655 – (18:2 + 1). +5]: 

= 303 – 3.[655 – (9 + 1).64 + 5]:100

= 303 – 3.[655 – 10.64 + 5]:100

= 303 – 3[655 – 640 + 5]:100

= 303 – 3[15 + 5]:100

= 303 – 3.20:1

= 303 – 60

= 243

Bài 2: Tìm x ∈ Z  biết:

a)  22 + (x + 3) = 52

4 + (x + 3) = 25

x + 3 = 25 – 4

x + 3  = 21

x = 21 -3

x = 18

Vậy x = 18

b) 125 – 5(4 + x) = 15

5(4 + x) = 125 – 15

5(4 + x) = 110

4 + x = 110: 5

4 + x = 22

x = 22 – 4 

x = 18

Vậy x = 18

c) (15 + x):3 = 315 : 312

(15 + x):3 = 33

15 + x = 33.3

15 + x = 34

15 + x = 81

x = 81 – 15

x = 66

Vậy x = 66

d)  2x + 1 – 2x = 32

 2x.2 – 2x = 32

2x.(2 – 1) = 32  

2x = 32

2x = 25 

x = 5

Vậy x = 5

Bài 3:

Lời giải:

Gọi số túi bi của bạn Vinh là x (x ∈ N*)

Vì chia đều 48 viên bi đỏ, 30 viên bi xanh và 66 viên bi vàng vào các túi bi nên 48 x; 30 x; 66 x hay x là ước chung của 48; 30;66.

Vì số túi bi chia được là lớn nhất nên x là ước chung lớn nhất của 48; 30; 66.

Ta có:

48 = 2.2.2.2.3 = 24.3  

30 = 2.3.5

66 = 2.3.11

ƯCLN (48; 30; 66) = 2.3 = 6

Vậy có thể chia nhiều nhất 6 túi bi sao cho số bi từng màu trong ba túi là bằng nhau.

Số bi màu đỏ trong mỗi túi là:

48:6 = 8 (viên)

Số bi màu xanh trong mỗi túi là:

30:6 = 5 (viên)

Số bi màu vàng trong mỗi túi là:

66:6 = 11 (viên)

Bài 4: Tìm các số tự nhiên x; y biết 2xy + x + 2y = 13.

Lời giải:

Ta có:

2xy + x + 2y = 13

⇒ 2xy + x + 2y + 1 = 13 +1

(2xy + 2y) + (x + 1) =14

2y(x + 1) + (x + 1) = 14

(x + 1)(2y + 1) =14

Vì x, y là các số tự nhiên nên x + 1 và 2y + 1 cũng là các số tự nhiên

Ta có: (x + 1)(2y + 1) = 1.14 = 2.7

Trường hợp 1: Với x + 1 = 1 và 2y + 1 = 14 

Ta có: x + 1 = 1 ⇒  x = 0

2y + 1 = 14 ⇒ 2y = 13 ⇒ y = [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề) (loại vì x, y là số tự nhiên)

Trường hợp 2: Với x + 1 = 14 và 2y + 1 = 1

Ta có: x + 1 = 14 ⇒ x = 14 – 1  

2y + 1 = 1 ⇒ 2y = 0 ⇒ y = 0 (thỏa mãn)

Trường hợp 3: Với x + 1 = 2 và 2y + 1 = 7

Ta có: x + 1 = 2 ⇒ x = 1

2y + 1 = 7 ⇒ 2y = 6 ⇒ y = 3 (thỏa mãn)

Trường hợp 4: Với x + 1 = 7 và 2y + 1 = 2

Ta có: x + 1 = 7 ⇒ x = 6

2y + 1 = 2 ⇒ 2y = 1⇒ y = [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)  (loại vì x, y là số tự nhiên)

Vậy ta tìm được hai cặp số (x; y) thỏa mãn là (13; 0) và (1; 3)

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 3

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Chân trời sáng tạo

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

Phần trắc nghiệm (4 điểm)

Câu 1: Viết tập hợp sau A = {x ∈ N | 12 ≤ x < 15}  bằng cách liệt kê các phần tử:

A) A =  {12; 13; 14; 15}

B) A =  {13; 14}

C) A =  {12; 13; 14}

D) A =  {13; 14; 15}

Câu 2: Kết quả của phép tính (42.3 – 20 : 5).3 là

A) 132

B) 130

C) 120

D) 126

Câu 3: Trong các tập hợp sau đây, tập hợp nào chỉ toàn số nguyên tố.

A)  A = {17; 19; 23; 27}

B) B =  {19; 23; 25; 31}

C) C = {17; 19; 23; 31}  

D) D = {17; 25; 27; 31}

Câu 4: Hình bình hành không có tính chất nào sau đây?

A) Bốn cạnh bằng nhau

B) Hai đường chéo cắt nhau tại trung điểm mỗi đường.

C) Hai cặp cạnh đối diện bằng nhau

D) Hai cặp cạnh đối diện song song.

Câu 5: Phân tích số 280 ra thừa số nguyên tố ta được kết quả là:

A)  22.5.7 

B) 23.3.5  

C)  23.3.7 

D) 23.5.7

Câu 6: Hình chữ nhật có chiều dài là 8cm và chiều rộng là 6cm có diện tích là:

A) 48 cm

B) 28 cm2

C) 24 cm2

D) 48 cm2 

Câu 7: Trong các khẳng định sau đây khẳng định nào sai:

A) Số chia hết cho cả 2 và 5 thì có tận cùng là 0.

B) Những số chia hết cho 3 thì chia hết cho 9.

C) Những số chia hết cho 9 thì chia hết cho 3.

D) Những số có tận cùng là 5 thì chia hết cho 5

Câu 8: Khẳng định nào sau đây là khẳng định đúng về hình chữ nhật

A) Bốn cạnh bằng nhau

B) Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

C) Hai đường chéo vuông góc với nhau.

D) Chu vi hình chữ nhật là tích của chiều dài và chiều rộng.

II. Phần tự luận (6 điểm)

Câu 1: Thực hiện các phép tính sau:

a)  6.32 – 3.23

b) 17.32 + 32.90 – 32.7

c) 120 : {54 – [50 : 2 – (32 – 2,4)]} 

d) 18:3 + 182 + 3.(51 : 17) 

Câu 2: Học sinh lớp 6C khi xếp hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó từ 35 đến 60 học sinh. Tính số học sinh lớp 6C.

Câu 3: Tìm x ∈ N biết:

a) 2x + 17 = 45

b) 35 – 5(x – 1) = 10

c) 24.(x – 16) = 122 

d)  (x2 – 10) : 5

Câu 4: Tìm tất cả các số tự nhiên n thỏa mãn 5n + 14 chia hết cho n + 2?

Những điều thú vị về cột cờ trường học có thể bạn chưa biết - Gia công sắt inox

Đáp án

Phần trắc nghiệm (4 điểm)

Câu 1: Viết tập hợp sau A = {x ∈ N | 12 ≤ x < 15} bằng cách liệt kê các phần tử:

A) A =  {12; 13; 14; 15}

B) A =  {13; 14}

C) A =  {12; 13; 14}

D) A =  {13; 14; 15}

Vì 12 ≤ x < 5 nên x ∈ {12; 13; 14} do đáp tập A = {12; 13; 14} .

Chú ý: x ≥ 12 nên ta lấy được cả 12

Câu 2: Kết quả của phép tính (42.3 – 20 : 5).3 là

A) 132

B) 130

C) 120

D) 126

 =  (42.3 – 20 : 5).3 = (16.3 – 4).3 = (48 – 4) .3 = 44.3 = 132

Câu 3: Trong các tập hợp sau đây, tập hợp nào chỉ toàn số nguyên tố.

A)  A = {17; 19; 23; 27}

B) B =  {19; 23; 25; 31}

C) C = {17; 19; 23; 31}  

D) D = {17; 25; 27; 31}

Giải thích:

A = {17; 19; 23; 27}  sai vì 27 là hợp số

B = {19; 23; 25; 31}  sai vì 25 là hợp số

C = {17; 19; 23; 31} đúng vì tất cả các số đã cho là số nguyên tố

D = {17; 25; 27; 31}  vì 25 và 27 là hợp số

Câu 4: Hình bình hành không có tính chất nào sau đây?

A) Bốn cạnh bằng nhau

B) Hai đường chéo cắt nhau tại trung điểm mỗi đường.

C) Hai cặp cạnh đối diện bằng nhau

D) Hai cặp cạnh đối diện song song.

Vì hình bình hành chỉ có các cạnh đối diện nhau thì mới bằng nhau.

Câu 5: Phân tích số 280 ra thừa số nguyên tố ta được kết quả là:

A)  22.5.7

B) 23.3.5 

C)  23.3.7

D)  23.5.7

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án Chân trời sáng tạo (3 đề)

 

Vậy 280 = 23.5.7

Câu 6: Hình chữ nhật có chiều dài là 8cm và chiều rộng là 6cm có diện tích là:

A) 48cm

B) 28 cm2 

C) 24 cm2 

D) 48 cm2 

Diện tích hình chữ nhật là:

S = 8.6 = 48 cm2

Câu 7: Trong các khẳng định sau đây khẳng định nào sai:

A) Số chia hết cho cả 2 và 5 thì có tận cùng là 0.

B) Những số chia hết cho 3 thì chia hết cho 9.

C) Những số chia hết cho 9 thì chia hết cho 3.

D) Những số có tận cùng là 5 thì chia hết cho 5

Giải thích:

A) Số chia hết cho cả 2 và 5 thì có tận cùng là 0.

Khẳng định A đúng vì số chia hết cho 5 có tận cùng là 0 và 5 còn số chia hết cho 2 có tận cùng là 0; 2; 4; 6; 8. Do đó số chia hết cho cả 2 và 5 phải có tận cùng là 0.

B) Những số chia hết cho 3 thì chia hết cho 9.

Sai vì 6 chia hết cho 3 nhưng không chia hết cho 9

C) Những số chia hết cho 9 thì chia hết cho 3.

Đúng vì những số chia hết cho 9 sẽ có tổng các chữ số của nó chia hết cho 9 nên tổng các chữ số của nó có dạng 9k. Mà 9k = 3.(3k) nên tổng các chữ số của số đó chia hết cho 3. Do đó số đó chia hết cho 3.

D) Những số có tận cùng là 5 thì chia hết cho 5

Đúng vì theo dấu hiệu chia hết cho 5 thì những số có tận cùng là 0 hoặc 5 thì chia hết cho 5

Câu 8: Khẳng định nào sau đây là khẳng định đúng về hình chữ nhật

A) Bốn cạnh bằng nhau

B) Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

C) Hai đường chéo vuông góc với nhau.

D) Chu vi hình chữ nhật là tích của chiều dài và chiều rộng.

Giải thích:

A) Bốn cạnh bằng nhau

Khẳng định A sai vì hình chữ nhật chỉ có các cạnh đối bằng nhau.

B) Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Đúng vì đây là tính chất của hình chữ nhật.

C) Hai đường chéo vuông góc với nhau.

Sai vì hình chữ nhật chỉ có hai đường chéo bằng nhau chứ không vuông góc.

D) Chu vi hình chữ nhật là tích của chiều dài và chiều rộng.

Sai vì tích của chiều dài và chiều rộng là diện tích hình chữ nhật, còn chu vi hình chữ nhật là hai lần tổng chiều dài và chiều rộng.

II. Phần tự luận

Câu 1: 

a)  6.32 – 3.23

= 6.9 – 3.8 = 54 – 24 = 30.

b) Cách 1:

17.32 + 32.90 – 32.7

= 32.(17 + 90 – 7) = 32.(107 – 7) = 32.100 = 3200

Cách 2: 

17.32 + 32.90 – 32.7

= 544 + 2880 – 224

= 3424 – 224 = 3200

c)  120 : {54 – [50 : 2 – ( 32 – 2.4]}

= 120: {54 – [25 – (9 – 8)]}

= 120:{54 – [25 – 1]}

= 120:{54 – 24}

= 120:30 = 4

d) 18:3 + 182 + 3. 

= 6 +182 + 3.3

= 6 + 182 + 9

= 197.

Câu 2: 

Lời giải:

Gọi số học sinh lớp 6C là a (a ∈ N; 35 ≤ a ≤ 60)  

Vì số học sinh xếp thành hàng 2, hàng 3, hàng 4, hàng 8 đều vừa đủ nên a là bội chung của 2; 3; 4; 8. Hay a ∈ BC(2; 3; 4; 8)

Ta tìm bội chung của 2; 3; 4; 8

Ta có:

2 = 2

3 = 3

4 = 2.2 = 22

8 = 2.2.2 = 23

Bội chung nhỏ nhất của 2; 3; 4; 8 là: 3. 23  = 3.8 = 24

Vì bội chung là bội của bội chung nhỏ nhất nên ta có:

BC(2; 3; 4; 8) = {0; 24; 48; 72; 96…}

Vì số học sinh trong khoảng từ 35 đến 60 nên a = 48.

Vậy lớp 6C có 48 học sinh.

Câu 3: Tìm x biết:

a) 2x + 17 = 45

2x = 45 – 17

2x = 28

x = 28:2

x = 14

Vậy x = 14

b) 35 – 5(x – 1) = 10

5(x – 1) = 35 – 10

5(x – 1) = 25

x – 1 = 25:5

x – 1= 5

x = 5 + 1

x = 6

Vậy x = 6

c) 24.(x – 16) = 122

24(x – 16) = 144

x – 16 = 144:24

x – 16 = 6

x = 6 + 16

x = 22

Vậy x = 22

d)  (x2 – 10) : 5 = 3

(x2 – 10) = 3.5

x2  – 10 = 15

x2 = 15 + 10

x2 = 25

x = 5

Vậy x = 5.

Câu 4: 

Lời giải:

Với mọi số tự nhiên n ta có (n + 2) chia hết cho (n + 2)

Do đó: 5(n + 2) chia hết cho (n + 2) hay (5n + 10) chia hết cho (n + 2)

Ta có: (5n + 14) = (5n + 10 + 4)

Để (5n + 14) chia hết cho (n + 2) thì 4 chia hết cho (n + 2) hay (n + 2) là ước của 4

Ư(4) = {1; 2; 4} 

n + 2

1

2

4

n

không tồn tại n

0

2

Vậy n = 0 hoặc n = 2 thì (5n + 14) chia hết cho (n + 2)

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 4

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Chân trời sáng tạo

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

Câu 1: Trong các số sau số nào là số tự nhiên?

A. \frac{4}{9}
B. 3\frac{1}{4}
C. 2022
D. 7,8

Câu 2: Cho M là tập hợp các số tự nhiên chẵn nhỏ hơn 10. Khẳng định nào sau đây là đúng?

A. 5 ∈ M
B. 10 ∈ M
C. 8 ∉ M
D. 6 ∈ M

Câu 3: Trong các số tự nhiên sau số nào là số nguyên tố

A.16
B. 17
C. 1
D. 33

Câu 4: Số nào sau đây là ước của 10:

A. 0
B. 5
C. 20
D. 40

Câu 5: Trong các tổng sau, tổng nào chia hết cho 3:

A. 400 + 30
B. 123 + 93
C. 13 + 27
D. 1.3.4 + 25

Câu 6: Tìm ý đúng:

A. 4 là ước 3
B. 2 là bội của 5
C. 8 là bội của 4
D. 9 là ước của 26

Câu 7: Trong các hình dưới đây hình vẽ tam giác đều là:

Câu 7

A. Hình a.
B. Hình b.
C. Hình c.
D. Hình d.

Câu 8: Hãy khoanh tròn vào phương án đúng nhất trong các phương án sau:

A. Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
B. Hình vuông là tứ giác có bốn góc bằng nhau.
C. Hình vuông là tứ giác có bốn cạnh bằng nhau.
D. Hình vuông là tứ giác có hai cạnh kề bằng nhau.

Câu 9: Ba đường chéo chính của lục giác ABCDEF là:

A. AB, CD, AC
B. AD, FC, EB
C. AB, CD, EF
D. FE, ED, DC

Câu 10: Yếu tố nào sau đây không phải của hình bình hành?

A. Hai cạnh đối bằng nhau
B. Hai cạnh đối song song
C. Hai góc đối bằng nhau
D. Hai đường chéo bằng nhau

Câu 11: Yếu tố nào sau đây không phải của hình chữ nhật?

A. Hai đường chéo vuông góc với nhau
B. Hai cạnh đối bằng nhau
C. Hai cạnh đối song song
D. Có bốn góc vuông

Câu 12: Chọn câu sai trong các câu dưới đây: Cho hình thoi ABCD

A. AB song song với CD và BC song song với AD.
B. AB = BC = CD= AD
C. AC và BD vuông góc với nhau
D. Bốn góc đỉnh A, B, C, D bằng nhau.

II. Tự luận (7 điểm):

Câu 13 (3 đ):

A) Biểu diễn phép tính sau về dạng một lũy thừa:

B) Tính: 49. 55 + 45.49

C) Cho số 234568, số trăm là?

D) Biểu diễn số 23 dưới dạng số La Mã.

E) Lớp 6A có số học sinh từ 30 đến 40 em khi xếp hàng 3, hàng 4, hàng 6 vừa đủ. Tính số học sinh của lớp 6A?

Câu 14 (2đ):

A) Phân tích số 75 ra thừa số nguyên tố?

B) Trong các số sau: 14; 2022; 52; 234; 1002; 2005. Những số nào chia hết cho 3?

C) Tìm BC (18; 30)

D) Rút gọn phân số \frac{48}{60}

Câu 15 (2 đ):

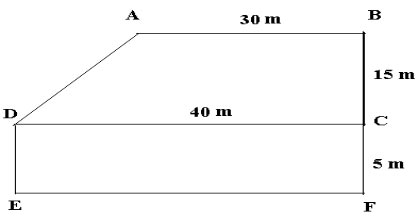
A) Mảnh vườn có kích thước như hình vẽ

Tính diện tích mảnh vườn đó?

B) Giá đất 1m2 là 500 000đ hỏi toàn bộ mảnh vườn giá bao nhiêu tiền?

Câu 15

Đáp án đề thi giữa kì 1 môn Toán lớp 6 năm 2022 – 2023

I. Trắc nghiệm

Câu

1

2

3

4

5

6

7

8

9

10

11

12

Đáp án

C

D

B

B

B

C

C

A

B

D

A

D

II. Tự luận:

Câu

Đáp án

Điểm

13A

5.5.5.5.5.5=56

0.5

13B

49. 55 + 45.49 = 49.(55+45)=49.100 = 4900

0.5

13C

Cho số 234568 số trăm là 2345

0.5

 

13 D

23 = XXIII

0.5

13E

Gọi số HS lớp 6A là x (x ∈ N, 30≤x≤40)

Ta có: x chia hết cho 3,4 và 6 nên x ∈ BC (3;4;6)

BCNN ( 3;4;6) = 22. 3 = 12

BC(3;4;6) = B(12) = {0;12;24;36;48 …}

Vì 30≤x≤40 nên x = 36

Vậy số HS lớp 6a là 36 (HS)

0.25

0.25

 

0.25

 

0.25

14A

 75 = 3.52

0.5

14B

Trong các số sau: 14; 2022; 52; 234; 1002; 2005.

Những số chia hết cho 3 là: 2022; 234; 1002.

 

0.5

14C

Tìm BC (18; 30)

BCNN(18; 30) = 2.32.5 = 90

BC (18; 30) = B(90) = { 0;90;180;270…}

0.25

 

0.25

14D

Thu gọn

\frac{48}{60}=\frac{48:12}{60:12}=\frac{4}{5}

Ư CLN(48;60) = 22 . 3 = 12

0.25

 

0.25

15a

Tính được diện tích ABCD là 525 m2

Tính diện tích DCFE là:200 m2

Tính diện tích hình: 725 m2

 

0.5

 

0.5

15b

Giá tiền: 725 . 500 000 = 362 500 000 đ

1.0

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 5

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Chân trời sáng tạo

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

I. Phần trắc nghiệm (4 điểm)

Câu 1. Viết tập hợp A các số tự nhiên lớn hơn 5 và nhỏ hơn 10

A. A = {6, 7, 8, 9}

B. A = {5, 6, 7, 8, 9}

C. A = { 6, 7, 8, 9, 10}

D. A = {6, 7, 8}

Câu 2. Viết tập hợp sau A = {x ∈ N | 9 < x < 13} bằng cách liệt kê các phần tử:

A. A = {10, 11, 12}

B. A = {9, 10, 11}

C. A = { 9, 10, 11, 12, 13}

D. A = {9, 10, 11, 12}

Câu 3: Trong các số sau: 59; 101; 355; 1341; 119; 29 những số nào là số nguyên tố?

A. 59; 101; 29

B. 101; 355; 119; 29

C. 59; 355; 1341; 29

D. 59; 101; 355

Câu 4: Số tự nhiên m chia cho 45 dư 20 có dạng là:

A. 45 + 20k

B. 45k + 20

C. 45 – 20k

D. 45k – 20

Câu 5: Phân tích 126 ra thừa số nguyên tố ta được kết quả:

A. 126 = {2^2}{.3^3}

B. 126 = {2.3^2}.7

C. 126 = {2.3^2}.5

D. 126 = 3.7.5

Câu 6: Tìm khẳng định đúng trong các khẳng định sau:

A. Một số chia hết cho 9 thì luôn chia hết cho 3

B. Nếu hai số chia hết cho 3 thì tổng của hai số đó chia hết cho 9

C. Mọi số chẵn thì luôn chia hết cho 5

D. Số chia hết cho 2 là số có chữ số tận cùng bằng 0; 2; 3; 4; 6; 8

Câu 7: Hình bình hành không có tính chất nào sau đây?

A. Hai cạnh đối song song với nhau

B. Hai cạnh đối bằng nhau

C. Bốn cạnh bằng nhau

D. Hai đường chéo chính bằng nhau

Câu 8: Diện tích hình thoi có độ dài hai đường chéo lần lượt bằng 10cm và 12cm là:

A. 60cm2

B. 60m

C. 60m2

D. 60cm

II. Phần tự luận (6 điểm)

Câu 1. Thực hiện các phép tính sau:

a) 12 : { 400 : [500 – (125 + 25 . 7)]}

b) 5 . 22 – 18 : 3

c) 18 : 3 + 182 + 3.(51 : 17)

d) 25 . 8 – 12.5 + 170 : 17 – 8

Câu 2: Tìm x biết:

a) 12 + (5 + x) = 20

b) 175 + (30 – x) = 200

c) 10 + 2x = 45 : 43

d) 10x + 22.5 = 102

Câu 3: Lớp 6A có 54 học sinh, lớp 6B có 42 học sinh và lớp 6C có 48 học sinh. Trong ngày khai giảng, ba lớp xếp thành các hàng dọc như nhau để diễu hành mà không có lớp nào có người lẻ hàng.

a. Tính số hàng dọc nhiều nhất có thể xếp được

b. Khi đó mỗi hàng có bao nhiêu học sinh?

Câu 4: Viết B = 4 + {2^2} + {2^3} + {2^4} + ... + {2^{20}} dưới dạng lũy thừa với cơ số 2

Đáp án Đề thi Toán lớp 6 giữa học kì 1

I. Phần trắc nghiệm (4 điểm)

Câu

Câu 1

Câu 2

Câu 3

Câu 4

Câu 5

Câu 6

Câu 7

Câu 8

Đáp án

A

A

A

B

B

A

C

A

II. Phần tự luận (6 điểm)

Câu 1

a) 12 : { 400 : [500 – (125 + 25 . 7)]}

12 : { 400 : [500 – (125 + 25 . 7)]} = 12 : { 400 : [500 – (125 + 175)]}

= 12 : { 400 : [500 – 300]} = 12 : { 400 : 200} = 12 : 2 = 6

b) 5 . 22 – 18 : 3 = 27 . 75 + 25 . 27 – 150 = 27. (75 + 25) – 150 = 27.100 – 150 = 270 – 150 = 120

c) 18 : 3 + 182 + 3.(51 : 17) = 197

d) 25 . 8 – 12.5 + 170 : 17 – 8 = 285

Câu 2.

a) 12 + (5 + x) = 20

5 + x = 20 – 12

5 + x = 8

x = 8 – 5 = 3

b) 175 + (30 – x) = 200

30 – x = 200 – 175

30 – x = 25

x = 30 – 25 = 5

c) 10 + 2x = 45 : 43

Đáp án: x = 11

d) 10x + 22.5 = 102

Đáp án x = 61

Câu 3

a) Vì số học sinh xếp đủ nên số hàng dọc là ước chung của số học sinh 3 lớp

Số hàng dọc nhiều nhất cũng là ước chung lớn nhất của số học sinh ba lớp

Ta có: 54 = 2.33     

42 = 2.3.7

48 = 24.3

ƯCLN (54; 42; 48) = 2.3 = 6

Vậy số hàng dọc nhiều nhất xếp được là 6 hàng

Câu 4

Ta có

\begin{aligned} &B=4+2^{2}+2^{3}+2^{4}+\ldots+2^{20} \\ &\Rightarrow 2 B=8+2^{3}+2^{4}+\ldots+2^{21} \\ &\Rightarrow 2 B-B=\left(8+2^{3}+2^{4}+\ldots+2^{21}\right)-\left(4+2^{2}+2^{3}+2^{4}+\ldots+2^{20}\right) \\ &\Rightarrow 2 B-B=2^{21}+8-\left(4+2^{2}\right) \\ &\Rightarrow B=2^{21} \end{aligned}

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Cánh diều

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 1

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 1)

A. Đề bài 

I. Phần trắc nghiệm (4 điểm) 

Câu 1: Tập hợp A các số tự nhiên x thỏa mãn 4 < x ≤ 9 là:

A. A = {4; 5; 6; 7; 8; 9}

B. A = {x ∈ N | 4 < x ≤ 9}

C. A = {5; 6; 7; 8}

D. A = {x ∈ N | 4 ≤ x ≤ 9} 

Câu 2: Có bao nhiêu số nguyên tố nhỏ hơn 25?

A. 9 số                 B. 10 số                C. 11 số               D. 12 số

Câu 3: Quan sát hình vẽ dưới đây và chọn câu trả lời đúng:

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

A.  a ∈ A              B. d ∈ A               C.  b ∈ A             D. c ∉ A

Câu 4: Viết tập hợp A các ước của số 16 là:

A. A = {1; 2; 3; 5}

B. A = {1; 2; 4; 8; 16}

C. A = {1; 2; 3; 4; 16}

D. A = {1; 2; 3; 4; 5; 6; 10; 16}

Câu 5: Đặc điểm nào dưới đây không phải là tính chất của hình vuông ABCD?

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

A. AB = BC = CD = DA

B. AB và CD song song với nhau

C. AD và CD song song với nhau

D. Hai đường chéo bằng nhau

Câu 6: Bác Hà uốn một sợi dây thép thành móc treo đồ có dạng hình thoi với độ dài cạnh bằng 25 cm. Hỏi bác Hà cần bao nhiên mét dây thép?

A. 1 cm                B. 100 cm             C. 1 m                  D. 100 m 

Câu 7: Công thức tính diện tích hình bình hành là:

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

A. S = a . b                    B. S = a . h           C. S = b . h                    D. S = a . b . h 

Câu 8: Một đoàn khách du lịch gồm 52 người muốn qua sông nhưng mỗi thuyền chỉ chở được 6 người (kể cả người lái thuyền). Hỏi cần ít nhất bao nhiêu thuyền để chở hết số khách?

A. 9 thuyền                    B. 10 thuyền        C. 11 thuyền        D. 12 thuyền 

II. Phần tự luận (6 điểm) 

Bài 1 (2 điểm):

1) Thực hiện các phép tính:

a) 25 . 8 – 15 . 5 + 160 : 16 – 10;

b) 2 . 52 – 3 : 710 + 54 : 33.

2) Phân tích các số 84, 120, 210 ra thừa số nguyên tố.

Bài 2 (1,5 điểm): Tính diện tích của phần được tô màu dưới đây biết: độ dài cạnh AB = 12 cm, BC = 4 cm và DG = 9 cm.

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Bài 3 (2 điểm): Bạn Nguyên có 30 chiếc bánh dẻo và 40 chiếc bánh nướng. Bạn Nguyên muốn chia số bánh vào các hộp sao cho số bánh mỗi loại trong các hộp là như nhau. Hỏi số hộp bánh nhiều nhất bạn Nguyên chia được là bao nhiêu hộp?

Bài 4 (0,5 điểm):Tìm số tự nhiên n để 3n + 4 chia hết cho n – 1.

Khi mà cả sân trường như đang im ắng chỉ nghe thấy tiếng gió thổi và đâu đó tiếng cô giáo giảng bài. Nhưng khi tiếng trống báo hiệu giờ ra chơi

—

B. Đáp án và hướng dẫn giải 

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: B

Câu 2: A

Câu 3: A

Câu 4: B

Câu 5: C

Câu 6: C

Câu 7: B

Câu 8: C

Hướng dẫn chi tiết 

Câu 1: 

Các số tự nhiên x thỏa mãn 4 < x ≤ 9 hay x lớn hơn 4 và nhỏ hơn hoặc bằng 9 là: 5, 6, 7, 8, 9. 

Ta viết tập hợp A bằng cách liệt kê các phần tử ta được: A = {5; 6; 7; 8; 9}. 

Ta viết tập hợp A bằng cách nêu dấu hiệu đặc trưng: A = {x ∈ N | x < 7}..

Chọn đáp án B.

Câu 2: 

Sử dụng sàng Eratosthenes ta đã biết các số nguyên tố nhỏ hơn 25 là: 2, 3, 5, 7, 11, 13, 17, 19, 23. 

Vậy có 9 số nguyên tố nhỏ hơn 25. 

Chọn đáp án A.

Câu 3: 

Quan sát hình vẽ: (đây là sơ đồ Ven)

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Ta thấy 

+ Các phần tử a, b, c nằm trong vòng kín biểu diễn tập hợp A, nên các phần tử a, b, c đều thuộc tập hợp A, ta viết a ∈ A, b ∈ A, c ∈ A. 

+ Các phần tử d, e nằm ngoài vòng kín biểu diễn tập hợp A nên các phần tử này không thuộc tập hợp A, ta viết d ∉ A, e ∉ A.

Vậy đáp án A đúng. 

Chọn đáp án A.

Câu 4: 

Để tìm các ước của 16, ta lấy 16 lần lượt chia cho các số tự nhiên từ 1 đến 16, các phép chia hết là: 16 : 1 = 16, 16 : 2 = 8, 16 : 4 = 4, 16 : 8 = 2, 16 : 16 = 1. 

Vậy các ước của 16 là: 1, 2, 4, 8, 16. 

Ta viết tập hợp A các ước của 16 là A = {1; 2; 4; 8; 16}. 

Chọn đáp án B.

Câu 5: 

Hình vuông ABCD có các tính chất:

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

+ Bốn cạnh bằng nhau: AB = BC = CD = DA 

+ Hai cạnh đối AB và CD, BC và AD song song với nhau

+ Hai đường chéo bằng nhau: AC = BD

+ Bốn góc ở các đỉnh A, B, C, D là góc vuông. 

Vậy hình vuông đã cho không có tính chất AD và CD song song với nhau.

Chọn đáp án C.

Câu 6: 

Số mét dây cần uốn chính là chu vi của hình thoi có độ dài cạnh bằng 25 cm và là: 

P = 4 . 25 = 100 cm = 1 m 

Vậy bác Hà cần 1 m dây thép để uốn. 

Chọn đáp án C.

Câu 7: 

Cho hình bình hành

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Diện tích của hình bình hành là S = a . h. 

Chọn đáp án B.

Câu 8: 

Vì mỗi thuyền chỉ chở được 6 người cả người lái đò nên mỗi thuyền chở được 5 người khách (trừ người lái đò). 

Có tất cả 52 người khách. Ta thực hiện phép chia: 52 : 5 = 10 (dư 2) 

Do đó dùng 10 thuyền để chở được 50 người khách và dư 2 người nên cần thêm một thuyền nữa để chở 2 người đó. 

Vậy cần ít nhất 10 + 1 = 11 thuyền để chở hết số khách. 

Chọn đáp án C.

II. Phần tự luận

Bài 1:

1) 

a) 25 . 8 – 15 . 5 + 160 : 16 – 10 

= 25 . 8 – 3 . 5 . 5 + 10 – 10

= 25 . 8 – 25 . 3 + (10 – 10)

= 25 . (8 – 3) + 0 = 25 . 5 = 125

b) 2 . 52 – 3 : 710 + 54 : 33

= 2 . 25 – 3 : 1 + 54 : 27 

= 50 – 3 + 2 

= 47 + 2 = 49

2) 

Ta phân tích các số ra thừa số nguyên tố bằng cách viết theo cột dọc hoặc rẽ nhánh. 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều                                                                           

Vậy: 

84 = 2 . 2 . 3 . 7 = 22 . 3 . 7

120 = 2 . 2 . 2 . 3 . 5 = 23 . 3 . 5

210 = 2 . 3 . 5 . 7

Bài 2:

Diện tích hình chữ nhật ABCD là: AB . BC = 12 . 4 = 48 (cm2)

Diện tích hình tam giác DEG là: DG . BC : 2 = 9 . 4 : 2 = 18 (cm2) (đường cao xuất phát từ E của tam giác DEG có độ dài bằng BC)

Diện tích phần tô màu là: 48 – 18 = 30 (cm2)

                                      Đáp số: 30 cm2.

Bài 3:

Gọi số hộp chia được là x (x là số tự nhiên khác 0)

Vì số bánh nướng trong mỗi hộp bằng nhau nên 40 ⁝ x.

Vì số bánh dẻo trong mỗi hộp bằng nhau nên 30 ⁝ x.

Vì x là số hộp bánh lớn nhất chia được nên x = ƯCLN(30, 40)

Ta có 30 = 2 . 3 . 5 và 40 = 23 . 5 nên ƯCLN(30, 40) = 2 . 5 = 10

Hay x = 10 (thỏa mãn)

Vậy số hộp bánh chia được nhiều nhất là 10 hộp.

Bài 4:

Vì 3n + 4 = 3n + 7 – 3 = 3n – 3 + 7 = 3(n – 1) + 7 

Do 3(n – 1) chia hết cho n – 1  (tính chất chia hết của một tích)

Nên để 3n + 4 chia hết cho n – 1 thì 7 phải chia hết cho n – 1 (tính chất chia hết của một tổng)

Hay (n – 1) thuộc Ư(7) = {1; 7}

Với n – 1 = 1 thì n = 2

Với n – 1 = 7 thì n = 8

Vậy với n = 2 hoặc n = 8 thì 3n + 4 chia hết cho n – 1.

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 2

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 2)

A. Đề bài 

I. Phần trắc nghiệm (4 điểm)

Câu 1: Tập hợp nào dưới đây có 5 phần tử?

A. A = {x ∈ N*| x > 3}

B. B = {x ∈ N| x < 6}

C. C = {x ∈ N | x ≤ 4}

D. D = {x ∈ N* | 4 < x ≤ 8}

Câu 2: Cho tập hợp M các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3. Phần tử nào dưới đây không thuộc tập hợp M?

A. 13                    B. 23                              C. 33                    D. 43 

Câu 3: Số 1 080 chia hết cho bao nhiêu số trong các số sau đây: 2, 3, 4, 5, 6, 8, 9, 12, 24, 25?

A. 10 số               B. 9 số                  C. 8 số                 D. 7 số

Câu 4: Hằng gấp được 97 ngôi sao và xếp vào các hộp, mỗi hộp 8 ngôi sao. Số ngôi sao còn thừa không xếp vào hộp là:

A. 5 ngôi sao

B. 1 ngôi sao

C. 6 ngôi sao 

D. 2 ngôi sao

Câu 5: Phân tích số 154 ra thừa số nguyên tố được:

A. 154 = 2 . 7 . 11 

B. 154 = 1 . 5 . 4 

C. 154 = 22 . 3 . 5 

D. 154 = 2 . 7 . 13

Câu 6: Hình nào dưới đây là hình vẽ chỉ tam giác đều?

A.[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

B. [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

C. [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

D. [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Câu 7: Hai đường chéo hình thoi có độ dài lần lượt bằng 16 cm và 12 cm. Diện tích của hình thoi là:

A. 90 cm2                       B. 96 cm2                       C. 108 cm2           D. 120 cm2

Câu 8: Chọn câu sai trong các câu dưới đây?

Cho hình vẽ 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Lục giác đều ABCDEG là hình có:

A. Các góc ở các đỉnh A, B, C, D, E, G, O bằng nhau.

B. Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.

C. Ba đường chéo chính cắt nhau tại điểm O.

D. Ba đường chéo chính bằng nhau: AD = BE = CG.

II. Phần tự luận (6 điểm) 

Bài 1 (2 điểm):

1) Thực hiện các phép tính:

a) 30 . 75 + 25 . 30 – 150;

b) 160 – (4 . 52 – 3 . 23);

c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220.

2) Tìm BCNN của các số 28, 54.

Bài 2 (1,5 điểm): Tính diện tích của hình H gồm hình bình hành ABCD và hình chữ nhật DCNM, biết hình chữ nhật DCNM có chu vi bằng 180 cm và chiều dài MN gấp 4 lần chiều rộng CN.

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Bài 3 (2 điểm):Một đội y tế gồm 48 bác sĩ và 108 y tá. Hỏi có thể chia đội y tế thành nhiều nhất bao nhiêu tổ để số bác sĩ và y tá được chia đều vào các tổ?

Bài 4 (0,5 điểm):Chứng tỏ A chia hết cho 6 với A = 2 + 22 + 23 + 24 + … + 2100.

—

B. Đáp án và hướng dẫn giải 

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: C

Câu 2: A

Câu 3: B

Câu 4: B

Câu 5: A

Câu 6: D

Câu 7: B

Câu 8: A

Hướng dẫn chi tiết 

Câu 1: 

Viết các tập hợp đã cho dưới dạng liệt kê các phần tử ta được

A = {4; 5; 6; … }    (tập hợp A các số tự nhiên lớn hơn 3)

B = {0; 1; 2; 3; 4; 5} (tập hợp B các số tự nhiên nhỏ hơn 6)

C = {0; 1; 2; 3; 4}   (tập hợp C các số tự nhiên nhỏ hơn hoặc bằng 4)

D = {5; 6; 7; 8}   (tập hợp D các số tự nhiên lớn hơn 4 và nhỏ hơn hoặc bằng 8)

Vậy ta thấy tập hợp C có 5 phần tử. 

Chọn đáp án C. 

Câu 2: 

Tập hợp M gồm các số tự nhiên lớn hơn 14, nhỏ hơn 45 và có chứa chữ số 3.

Ta thấy các số 13, 23, 33, 43 đều có chứa chữ số 3, nhưng 13 < 14 nên 13 không thuộc tập hợp M. 

Chọn đáp án A. 

Câu 3: 

Số 1 080 có chữ số tận cùng là 0 nên nó chia hết cho cả 2 và 5.

Số 1 080 có tổng các chữ số là 1 + 0 + 8 + 0 = 9 chia hết cho 3 và 9 nên nó chia hết cho cả 3 và 9. 

Ngoài ra: 1 080 : 4 = 270; 1 080 : 6 = 180; 1 080 : 8 = 135; 1 080 : 12 = 90; 1 080 : 24 = 45; 1 080 : 25 = 43 (dư 5).

Vậy số 1 080 chia hết cho các số: 2, 3, 4, 5, 6, 8, 9, 12, 24. 

Do đó nó chia hết cho 9 số trong các số đã cho. 

Chọn đáp án B. 

Câu 4: 

Mỗi hộp có 8 ngôi sao nên ta thực hiện phép chia: 

97 : 8 = 12 (dư 1) 

Vậy còn thừa 1 ngôi sao không xếp vào hộp. 

Chọn đáp án B. 

Câu 5: 

Ta phân tích 154 ra thừa số nguyên tố: 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Vậy 154 = 2 . 7 . 11.

Chọn đáp án A. 

Câu 6: 

Tam giác đều là hình tam giác có 3 cạnh bằng nhau và 3 góc bằng nhau, vậy trong các hình đã cho, hình vẽ D chỉ tam giác đều. 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Chọn đáp án D. 

Câu 7: 

Diện tích hình thoi bằng [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều  tích độ dài hai đường chéo.

Vậy diện tích của hình thoi có độ dài hai đường chéo lần lượt là 16 cm và 12 cm là: 

S = [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều.16.12 = 96 (cm2).

Chọn đáp án B. 

Câu 8: 

Lục giác đều ABCDEG có các tính chất: 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

+ Các góc ở các đỉnh A, B, C, D, E, G bằng nhau.

+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA.

+ Ba đường chéo chính AD, BE, CG cắt nhau tại điểm O.

+ Ba đường chéo chính bằng nhau: AD = BE = CG.

Vậy đáp án A sai (vì góc ở đỉnh O không bằng các góc ở đỉnh của lục giác).

Chọn đáp án A.

II. Phần tự luận

Bài 1:

1) 

a) 30 . 75 + 25 . 30 – 150 

= 30 . (75 + 25) – 150 

= 30 . 100 – 150 

= 3 000 – 150 = 2 850

b) 160 – (4 . 52 – 3 . 23) 

= 160 – (4 . 25 – 3 . 8) 

= 160 – (100 – 24) 

= 160 – 76 = 84

c) [36 . 4 – 4 . (82 – 7 . 11)2] : 4 – 20220

= [36 . 4 – 4 . (82 – 77)2] : 4 – 1

= [36 . 4 – 4 . 52] : 4 – 1 

= [36 . 4 – 4 . 25] : 4 – 1 

= [4 . (36 – 25)] : 4 – 1

= 4 . 11 : 4 – 1 = 11 – 1 = 10

2) 

Đề tìm BCNN của 28 và 54, ta phân tích các số đó ra thừa số nguyên tố. 

Ta có: 28 = 4 . 7 = 22 . 7

54 = 6 . 9 = 2 . 3 . 32 = 2 . 33

Vậy BCNN(28, 54) = 22 . 33 . 7 = 4 . 27 . 7 = 756. 

Bài 2:

Nửa chu vi hình chữ nhật DCNM là: 180 : 2 = 90 (cm)

Khi đó: MN + CN  = 90 (cm)

Chiều dài MN gấp 4 lần chiều rộng CN

Tổng số phần bằng nhau là: 1 + 4 = 5 (phần)

Chiều dài MN (hay CD) của hình chữ nhật DCNM là: 90 : 5 . 4 = 72 (cm)

Chiều rộng CN (hay DM) của hình chữ nhật DCNM là: 90 – 72 = 18 (cm)

Diện tích hình chữ nhật DCMN là: 18 . 72 = 1 296 (cm2)

Diện tích hình bình hành ABCD là: 72 . 20 = 1 440 (cm2)

Diện tích hình H là: 1 296 + 1 440 = 2 736 (cm2). 

Bài 3:

Gọi x là số tổ nhiều nhất được chia (x là số tự nhiên khác 0).

Vì số bác sĩ được chia đều vào mỗi tổ nên 48 ⁝ x 

Số y tá được chia đều vào mỗi tổ nên 108 ⁝ x 

Do đó x là ước chung của 48 và 108, mà x là nhiều nhất nên x là ƯCLN của 48 và 108. 

Ta có: 48 = 24 . 3

108 = 22 . 33

Suy ra ƯCLN(48, 108) = 22 . 3 = 12 hay x = 12 (thỏa mãn).

Vậy có thể chia được nhiều nhất 12 tổ.

Bài 4:

A = 2 + 22 + 23 + 24 + … + 2100

A = (2 + 22) + (23 + 24) + … + (299 + 2100)

A = 6 + 22 . (2 + 22) + … + 298 . (2 + 22)

A = 6 + 22 . 6 + … + 298 . 6

A = 6 . (1 + 22 + … + 298)

Vậy A chia hết cho 6 (theo tính chất chia hết của một tích). 

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 3

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 3)

A. Đề bài 

I. Phần trắc nghiệm (4 điểm) 

Câu 1: Tập hợp A các số tự nhiên nhỏ hơn 7 được viết là:

A. A = {x ∈ N* | x < 7}

B. A = {x ∈ N | x < 7}

C. A = {x ∈ N* | x ≤ 7}

D. A = {x ∈ N | x > 7}

Câu 2: Cho tập hợp B = {1; 8; 12; 21}. Phần tử nào dưới đây không thuộc tập hợp B?

A. 1                      B. 12                    C. 21                    D. 18

Câu 3: Trong các số tự nhiên dưới đây, số nào là số nguyên tố?

A. 101                  B. 114                  C. 305                  D. 303

Câu 4: Số nào dưới đây chia hết cho 5 nhưng không chia hết cho 3?

A. 120                  B. 195                  C. 215                  D. 300 

Câu 5: Diện tích của hình vuông có độ dài cạnh a = 4 . 5 + 22 . (8 – 3) (cm) là:

A. 160 cm2           B. 400 cm2           C. 40 cm2             D. 1 600 cm2 

Câu 6: Hình bình hành không có tính chất nào dưới đây?

A. Hai cạnh đối bằng nhau

B. Hai cạnh đối song song với nhau

C. Hai góc đối bằng nhau

D. Bốn cạnh bằng nhau 

Câu 7: Cho 24 ⁝ (x + 6) và 3 ≤ x < 8, với x là số tự nhiên. Vậy x có giá trị bằng:

A. 5                      B. 6                      C. 7                      D. 8 

Câu 8: Cho hình thoi có độ dài hai đường chéo bằng 8 cm và 10 cm. Diện tích của hình thoi là:

A. 40 cm2              B. 60 cm2             C. 80 cm2              D. 100 cm2 

II. Phần tự luận (6 điểm) 

Bài 1 (2 điểm): Thực hiện phép tính:

a) 162 + 475 + 173 + 227 + 525 + 438;

b) 25 . 6 + 5 . 5 . 29 – 45 . 5;

c) 2 . [(7 – 33 : 32) : 22 + 99] – 100;

d) (52022 + 52021) : 52021.

Bài 2 (1 điểm): Một mảnh vườn hình chữ nhật có chiều dài bằng 40 m và chu vi bằng 140 m. Tính diện tích của mảnh vườn hình chữ nhật đó.

Bài 3 (2 điểm):Lớp 6A có 42 học sinh, lớp 6B có 54 học sinh và lớp 6C có 48 học sinh. Cô phụ trách đã xếp đều số học sinh của 3 lớp thành một số hàng như nhau. Tính số hàng nhiều nhất có thể xếp được.

Bài 4 (1 điểm):Chứng tỏ rằng: (1028 + 8) ⁝ 9.

Những hình ảnh xa trường bồi hồi và xúc động nhất

B. Đáp án và hướng dẫn giải 

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 8 = 4 điểm)

Câu 1: B

Câu 2: D

Câu 3: A

Câu 4: C

Câu 5: D

Câu 6: D

Câu 7: B

Câu 8: A

Hướng dẫn chi tiết

Câu 1: 

Gọi x là số tự nhiên thuộc tập hợp A.

Ta có x là số tự nhiên nên x ∈ N

Mà các số tự nhiên thuộc tập hợp A nhỏ hơn 7 nên x < 7. 

Vậy ta viết tập hợp A như sau: A = .

Chọn đáp án B.

Câu 2: 

Ta có: B = {1; 8; 12; 21} 

Nhận thấy số 18 không phải là phần tử của tập hợp B nên 18 không thuộc tập hợp B. 

Chọn đáp án D. 

Câu 3: 

Lý thuyết: Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó. 

Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước. Một số là hợp số thì không thể là số nguyên tố. 

Trong các số đã cho, ta thấy: 

+) 114 có chữ số tận cùng là 4 nên nó chia hết cho 2, do đó 114 là hợp số vì ngoài hai ước là 1 và 114 thì nó còn có thêm ít nhất một ước nữa là 2.

+) 305 có chữ số tận cùng là 5 nên nó chia hết cho 5, do đó 305 là hợp số vì ngoài hai ước là 1 và 305 thì nó còn có thêm ít nhất một ước nữa là 5. 

+) 303 có tổng các chữ số là 3 + 0 + 3 = 6 chia hết cho 3 nên nó chia hết cho 3, do đó 303 là hợp số vì ngoài hai ước là 1 và 303 thì nó còn có thêm ít nhất một ước nữa là 3. 

+) Số 101 lớn hơn 1, chỉ có hai ước là 1 và 101 nên nó là số nguyên tố. 

Chọn đáp án A.

Câu 4: 

Các số 120, 195, 215, 300 đều chia hết cho 5 (vì có tận cùng là 0 hoặc 5).

Số 215 có tổng các chữ số là 2 + 1 + 5 = 8 không chia hết cho 3 nên 215 không chia hết cho 3. 

Vậy số 215 chia hết cho 5 nhưng không chia hết cho 3.

Chọn đáp án C. 

Câu 5: 

Ta có: a = 4 . 5 + 22 . (8 – 3) = 20 + 4 . 5 = 20 + 20 = 40 (cm)

Diện tích hình vuông có cạnh a là:

S = a . a = 40 . 40 = 1 600 (cm2).

Chọn đáp án D.

Câu 6: 

[Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều

Hình bình hành ABCD có các tính chất: 

+ Hai cạnh đối AB và CD, AD và BC song song với nhau. 

+ Hai cạnh đối AB và CD, AD và BC bằng nhau. 

+ Hai góc ở đỉnh A và C bằng nhau, hai góc ở đỉnh B và D bằng nhau (hai góc đối bằng nhau) 

Do đó hình bình hành không có tính chất: Bốn cạnh bằng nhau.

Chọn đáp án D.

Câu 7: 

Ta có: x là số tự nhiên thỏa mãn 3 ≤ x < 8

Khi đó: x ∈ {3; 4; 5; 6; 7}

Lại có: 24 ⁝ (x + 6) (*)

Ta thử thay lần lượt các giá trị của x vào (*), ta thấy x = 6 thỏa mãn vì x + 6 = 6 + 6 = 12, 24 chia hết cho 12. 

Vậy x có giá trị là 6. 

Chọn đáp án B.

Câu 8: 

Diện tích hình thoi bằng [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều  lần tích độ dài hai đường chéo.

Do đó diện tích hình thoi có độ dài hai đường chép bằng 8 cm và 10 cm là:

S = [Năm 2021] Đề thi Giữa kì 1 Toán lớp 6 có đáp án (3 đề) | Cánh diều.8.10 = 40 (cm2)

Chọn đáp án A.

II. Phần tự luận 

Bài 1:

a) 162 + 475 + 173 + 227 + 525 + 438

= (162 + 438) + (475 + 525) + (173 + 227)

= 600 + 1 000 + 400

= (600 + 400) + 1 000

= 1 000 + 1 000

= 2 000

b) 25 . 6 + 5 . 5 . 29 – 45 . 5

= 25 . 6 + 25 . 29 – 9 . 5 . 5  

= 25 . 6 + 25 . 29 – 25 . 9 

= 25 . (6 + 29 – 9) 

= 25 . 26 = 650

c) 2 . [(7 – 33 : 32) : 22 + 99] – 100

= 2 . [(7 – 3) : 4 + 99] – 100 

= 2 . [4 : 4 + 99] – 100 

= 2 . (1 + 99) – 100 

= 2 . 100 – 100 = 100

d) (52 022 + 52 021) : 52 021

= 52 022 : 52 021 + 52 021 : 52 021

= 52 022 – 2 021  + 52 021 – 2 021 

= 51 + 50

= 5 + 1 = 6

Bài 2:

Nửa chu vi của hình chữ nhật là: 140 : 2 = 70 (m)

Chiều rộng mảnh vườn hình chữ nhật là: 70 – 40 = 30 (m)

Diện tích mảnh vườn hình chữ nhật là: 40 . 30 = 1 200 (m2). 

Bài 3:

Gọi số hàng có thể xếp là x (x ∈ N* ; hàng)

Theo đề bài có: 42 ⁝ x; 54 ⁝ x; 48 ⁝ x và x lớn nhất nên x là ƯCLN của 42, 54 và 48.

Ta tìm ƯCLN này bằng cách phân tích các số 42, 54, 48 ra thừa số nguyên tố. 

Ta có: 42 = 2 . 3 . 7 

54 = 2 . 33 

48 = 24 . 3 

Suy ra ƯCLN(42, 54, 48) =  2 . 3 = 6 hay x = 6 (thỏa mãn).

Vậy có thể xếp được nhiều nhất là 6 hàng để thỏa mãn yêu cầu bài toán. 

Bài 4:

Có 1028 có dạng 10….000 (28 chữ số 0) nên 1028 + 8 có dạng 10….008 (27 chữ số 0) nên số 1028 + 8 sẽ chia hết cho 9 (tổng các chữ số bằng 9).

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 4

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 4)

I: Trắc nghiệm khách quan (4đ). Khoanh tròn vào chữ cái đứng trước câu trả lời mà em cho là đúng nhất.

Câu 1: Tập hợp P các số tự nhiên lớn hơn 6 có thể viết là.

A. P ={x ∈ N | x < 7}

B. C. P ={x ∈ N | x > 7}

B. P ={x ∈ N | x 7}

D. P ={x ∈ N | x 7}

Câu 2: Chữ số 5 trong số 2358 có giá trị là.

A. 5000
B. 500
C. 50
D. 5

Câu 3: Chỉ ra cặp số tự nhiên liền trước và liền sau của số 99.

A. (97; 98)
B. (98; 100)
C. (100; 101)
D. (97; 101)

Câu 4: Cho tập A={ 2; 3; 4; 5}. Phần tử nào sau đây thuộc tập A.

A. 1
B. 3
C. 7
D. 8

Câu 5: Tổng 15 + 30 chia hết cho số nào sau đây:

A. 2 và 3
B. 2 và 5
C. 3 và 5
D. 2; 3 và 5

Câu 6: Cho 18 ⁝ x và 7 ≤ x < 18 . Thì x có giá trị là:

A. 2
B. 3
C. 6
D. 9

Câu 7: Trong các số tự nhiên sau số nào là số nguyên tố

A. 16
B. 27
C. 2
D. 35

Câu 8: ƯCLN (3, 4) là:

A. 1
B. 3
C. 4
D. 12

Câu 9: Kết quả phép tính 13 – 5 + 3 là:

A. 11
B. 12
C. 8
D. 10

Câu 10: Kết quả phép tính 18: 32 . 2 là:

A. 18
B. 4
C. 1
D. 12

Câu 11: Kết quả phép tính 24 . 2 là:

A. 24
B. 23
C. 26
D. 25

Câu 12: Số 75 được phân tích ra thừa số nguyên tố là:

A. 2 . 3 . 5
B. 3 . 5 . 7
C. 3 . 52
D. 32 . 5

Câu 13: Cho x ∈ {5, 16, 25, 135} sao cho tổng 20 + 35 + x không chia hết cho 5. Thì x là:

A. 5
B. 16
C. 25
D. 135

Câu 14: BCNN của 2.33 và 3.5 là:

A. 2 . 33 . 5
B. 2 . 3 . 5
C. 3. 33
D. 33

Câu 15: Trong tam giác đều mỗi góc có số đo bằng:

A. 600
B. 450
C. 900
D. 300

Câu 16: Trong hình vuông có:

A. Hai cạnh đối bằng nhau
B. Hai đường chéo bằng nhau
C. Bốn cạnh bằng nhau
D. Hai đường chéo vuông góc

Câu 17:

Cho H.1. Công thức tính chu vi của hình chữ nhật là:

A. C = 4a
B. C = \frac{1}{2} (a + b)
C. C = \frac{1}{2}ab
D. 2(a + b)

Đề thi giữa học kì 1 Toán lớp 6

Câu 18:

Cho H.2. Công thức tính diện tích của hình bình hành là:

A. S = ab
B. S = \frac{1}{2}ah
C. S = \frac{1}{2}bh
D. S = ah

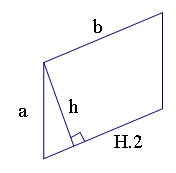
Đề thi giữa học kì 1 lớp 6 môn Toán

Câu 19: Cho hình thoi, biết độ dài hai đường chéo là 2cm và 4cm. Thì diện tích hình thoi là:

A. 4
B. 6
C. 8
D. 2

Câu 20: Cho hình bình hành ABCD (H.3). Biết AB = 3cm, BC = 2cm

Chu vi của hình bình hành ABCD là:

A. 6
B. 10
C. 12
D. 5

Đề thi giữa học kì 1 Toán lớp 6

Câu 21: Thực hiện phép tính

a) 125 + 70 + 375 +230

b) 49. 55 + 45.49

c) 120:\left\{54-\left[50:2-\left(3^2-2.4\right)\right]\right\}

Câu 22: Học sinh lớp 6A xếp thành 4; 5; 8 đều vừa đủ hàng. Hỏi số HS lớp 6A là bao nhiêu? Biết rằng số HS nhỏ hơn 45.

Câu 23: Mảnh vườn hình chữ nhật có chiều rộng bằng 8m và diện tích bằng 120m2. Tính chu vi mảnh vườn hình chữ nhật đó?

Câu 24: Tìm tất cả các số tự nhiên n thoả mãn 5n + 14 chia hết cho n + 2?

Đáp án Đề thi Toán lớp 6 giữa học kì 1

I. Trắc nghiệm: Từ câu 1 đến câu 20. Mỗi câu đúng 0,25 điểm

Câu 1 2 3 4 5 6 7 8 9 10
ĐA D C B B C D C A A A
Câu 11 12 13 14 15 16 17 18 19 20
ĐA D C B A A C D C A C

II. Tự luận

Câu   Điểm

21

Thực hiện phép tính

a) 125 + 70 + 375 +230 = (125 + 375) + (70 + 230) = 500 + 300 = 800

0,5

b) 49. 55 + 45.49 =49(55+45) =4900

0,5

c) 120:\left\{54-\left[50:2-\left(3^2-2.4\right)\right]\right\}

=120\left\{54-\left[50:2-\left(9-8\right)\right]\right\}

=120:\left\{54-\left[25-1\right]\right\}=120:\left\{54-24\right\}

1

22

 

 

 

Gọi số HS của lớp 6A là x (0<x<45)

0,5

 

Vì x ⁝ 4, x ⁝ 5, x ⁝ 8 nên x∈ BC(4;5;8)

0,5

 

BCNN(4;5;8) = 23.5 = 40

Do (0 < x < 45) nên số học sinh của lớp 6A là 40 HS

0,5

23

Chiều dài mảnh vườn hình chữ nhật là:

120 : 8 = 15 m

Chu vi mảnh vườn hình chữ nhật là:

2(8+15)= 46 m

0,5

 

 

0,5

 

24

Với mọi n ta có n+2 ⁝ n+2n

nên 5(n+2) =5n+10 ⁝ n+2 =>5n+14=5n+10+4 ⁝ n+2 khi 4 chia hết cho n+2 do đó n+2 thuộc Ư(4) ={1,2,4}

Giải từng trường hợp ta được: n= 0;2

 

Đề thi Giữa kì 1 Toán lớp 6 có đáp án năm 2023 – Đề 5

Phòng Giáo dục và Đào tạo …

Đề thi Giữa kì 1 – Cánh diều

Năm học 2023 – 2024

Bài thi môn: Toán lớp 6

Thời gian làm bài: 60 phút

(không kể thời gian phát đề)

(Đề số 5)

I. Phần trắc nghiệm (6 điểm)

Câu 1: Phép nhân 7.7.7.7.7 được viết rút gọn thành:

A. 57

B. 5.7

C. 7.5

D. 75

Câu 2: Số phần tử của tập hợp A = {3; 4; 5; …; 78; 79; 80} là:

A. 78 phần tử

B. 79 phần tử

C. 80 phần tử

D. 81 phần tử

Câu 3: Cho 4 số tự nhiên 1831; 5930; 1940; 1848. Trong 4 số trên có bao nhiêu số vừa chia hết cho 2, vừa chia hết cho 5?

A. 4 số

B. 3 số

C. 2 số

D. 1 số

Câu 4: Tập hợp ước số của số 18 là:

A. Ư(18) = {1; 2; 3; 5; 6; 9; 18}

B. Ư(18) = {1; 2; 3; 4; 6; 9; 18}

C. Ư(18) = {1; 2; 3; 6; 9; 18}

D. Ư(18) = {1; 2; 3; 9; 18; 36}

Câu 5: Kết quả của phép tính 25.23 là:

A. 28

B. 28

C. 82

D. 82

Câu 6: Cho hình lục giác đều ABCDEF tâm O, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có một cạnh là cạnh của lục giác đều?

Đề thi giữa kì 1 Toán 6 năm học 2021 - 2022 sách Cánh Diều - Đề 4

A. 5 tam giác

B. 6 tam giác

C. 7 tam giác

D. 8 tam giác

Câu 7: Trong các số sau 7, 18, 13, 19, 6, 10; có bao nhiêu số là số nguyên tố?

A. 2 số

B. 3 số

C. 4 số

D. 5 số

Câu 8: Trong các hình dưới đây, có bao nhiêu hình là hình bình hành?

Đề thi giữa kì 1 Toán 6 năm học 2021 - 2022 sách Cánh Diều - Đề 4

A. 6 hình

B. 5 hình

C. 4 hình

D. 3 hình

Câu 9: Chu vi của hình vuông có cạnh bằng 70cm là:

A. 280cm

B. 4900cm

C. 2800dm

D. 28m

Câu 10: Điều kiện để số a trong biểu thức A = 15 + a + 5 + 10 chia hết cho 5 là:

A. a là số tự nhiên chẵn

B. a là số có tận cùng bằng 0 hoặc 5

C. a là số tự nhiên bất kì

D. a là số tự nhiên lẻ

Câu 11: Có bao nhiêu số tự nhiên thỏa mãn 12 ≤ x < 20?

A. 6 số

B. 7 số

C. 8 số

D. 9 số

Câu 12: Diện tích của hình bình hành bằng 360cm2. Độ dài cạnh đáy của hình bình hành biết chiều cao bằng 15cm là:

A. 30cm

B. 28cm

C. 26cm

D. 24cm

II. Phần tự luận (4 điểm)

Câu 13 (1,5 điểm): Thực hiện phép tính:

a) 55 + 672 + 28 + 345

b) 33.5 + 33.7 – 33.2

c) 28 : [5 + (17 – 15).32 + 81 : 9]

Câu 14 (1 điểm): Tìm x, biết:

a) 89 + (138 – x) = 90

b) 3x + 20 = 65

Câu 15 (2 điểm): Tính diện tích của miếng bìa H được tạo bởi hình vuông và hình chữ nhật có kích thước như hình vẽ dưới đây:

 

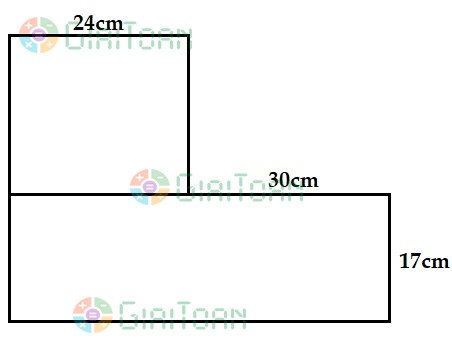
Đề thi giữa kì 1 Toán 6 năm học 2021 - 2022 sách Cánh Diều - Đề 4

Câu 16 (0,5 điểm): Chứng tỏ rằng số A = 2 + 22 + 23 + … + 260 chia hết cho 3 và 7.

Đáp án đề thi giữa học kì 1 môn Toán lớp 6 Đề 5

I. Phần trắc nghiệm

Câu 1: D

Câu 2: A

Câu 3: C

Câu 4: C

Câu 5: A

Câu 6: B

Câu 7: B

Câu 8: C

Câu 9: A

Câu 10: B

Câu 11: C

Câu 12: D

II. Phần tự luận

Câu 13:

a) 55 + 672 + 28 + 345 = (55 + 345) + (672 + 28) = 400 + 700 = 1100

b) 33.5 + 33.7 – 33.2 = 33.(5 + 7 – 2) = 33.10 = 330

c) 28 : [5 + (17 – 15).32 + 81 : 9]

= 28 : [5 + 2.9 + 9] = 28 : [28 : [5 + (17 – 15).32 + 81 : 9]] = 28 : 32 = 28 : 25 = 23 = 8

Câu 14:

a) 89 + (138 – x) = 90

138 – x = 90 – 89

138 – x = 1

x = 138 – 1

x = 137

b) 3x + 20 = 65

3x = 65 – 20

3x = 45

x = 45 : 3

x = 15

Câu 15:

Diện tích hình vuông là: 24.24 = 576cm2

Chiều dài hình chữ nhật là: 24 + 30 = 54cm

Diện tích hình chữ nhật là: 54.17 = 918cm2

Diện tích miếng bìa là: 576 + 918 = 1494cm2

Câu 16:

  • Có A = 2 + 22 + 23 + … + 260

A = 2.(1 + 2) + 23.(1 + 2) + … + 259.(1 + 2)

A = 2.3 + 23.3 + … + 259.3

A = 3.(2 + 23 + … + 259) chia hết cho 3

  • Có A = 2 + 22 + 23 + … + 260

A = 2.(1 + 2 + 22) + 24.(1 + 2 + 22) + … + 258.(1 + 2 + 22)

A = 2.7 + 24.7 + … + 258.7

A = 7.(2 + 24 + … + 258) chia hết cho 7

Bài liên quan:

Leave a Comment

Back to Top
Menu