Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Tìm khẳng định đúng

Câu hỏi:

Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Tìm khẳng định đúng

A. AC là tiếp tuyến của (B; BA).

Đáp án chính xác

B. AB là tiếp tuyến của (A; AC).

C. BC là tiếp tuyến của (A; AC).

D. BC là tiếp tuyến của (A; AB).

Trả lời:

Đáp án ATam giác ABC có: $A{B}^2 + A{C}^2 = B{C}^2$ nên tam giác BAC vuông tại A.Ta có: AB ⊥ AC tại A và A thuộc đường tròn (B; BA).Suy ra: AC là tiếp tuyến của (B; BA).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho (O; R).Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi
   
   

   Câu hỏi:
   

   Cho (O; R).Đường thẳng d là tiếp tuyến của đường tròn (O; R) tại tiếp điểm A khi

   A. d ⊥ OA tại A và A ∈ (O)

   Đáp án chính xác

   B. d ⊥ OA

   C. A ∈ (O)

   D. d // OA

   Trả lời:

   Đáp án ANếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó
   
   

   Câu hỏi:
   

   Cho (O; 5cm). Đường thẳng d là tiếp tuyến của đường tròn (O; 5cm), khi đó

   A. Khoảng cách từ O đến đường thẳng d nhỏ hơn 5cm

   B. Khoảng cách từ O đến đường thẳng d lớn hơn 5cm

   C. Khoảng cách từ O đến đường thẳng d bằng 5cm

   Đáp án chính xác

   D. Khoảng cách từ đến O đường thẳng d bằng 6cm

   Trả lời:

   Đáp án CKhoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?
   
   

   Câu hỏi:
   

   Cho tam giác ABC có AC = 3cm, AB = 4cm, BC = 5cm. Vẽ đường tròn (C; CA). Khẳng định nào sau đây là đúng?

   A.Đường thẳng BC cắt đường tròn (C; CA) tại một điểm

   B.AB là cát tuyến của đường tròn (C; CA)

   C.AB là tiếp tuyến của (C; CA)

   Đáp án chính xác

   D. BC là tiếp tuyến của (C; CA)

   Trả lời:

    Đáp án C + Xét tam giác có:$B{C}^2 = 5^2 = 25; A{B}^2 + A{C}^2 = 4^2 + 3^2 = 25 \Rightarrow B{C}^{{}^2} = A{B}^2 + A{C}^2$⇒ ΔABC vuông tại A (Định lý Pytago đảo)⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI
   
   

   Câu hỏi:
   

   Cho tam giác cân ABC tại A; đường cao AH và BK cắt nhau tại I. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AI

   A. HK

   Đáp án chính xác

   B. IB

   C. IC
    

   D. AC

   Trả lời:

   Đáp án A
   
   +) Gọi O là trung điểm AI. Xét tam giác vuông AIK có
   
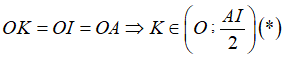
   +) Xét tam giác OKA cân tại O (vì OA=OK=R) có:
   $\widehat{OKA}=\widehat{OAK}$ (1)
   +) Xét tam giác CKB vuông tại K (vì $KB\perp AC$ ) có:
   H là trung điểm CB (vì tam giác ABC cân tại A có AH là đường cao nên đồng thời là đường trung tuyến)
   $\Rightarrow$KH là trung tuyến ứng với cạnh huyền BC
   $\Rightarrow \widehat{HKC}=\widehat{HCK} \left(2\right)$
   Từ (1) và (2) suy ra $\widehat{OKA}+\widehat{HKC}=\widehat{OAK}+\widehat{HCK}={90}^o$ (vì $AH\perp BC$)
   Mà $\widehat{OKA}+\widehat{HKC}+\widehat{OKH}={180}^o$ $\Rightarrow \widehat{OKH}={90}^o\Rightarrow OK\perp KH$ (**)
   Từ (*) và (**) suy ra HK là tiếp tuyến của (O)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau
   
   

   Câu hỏi:
   

   Cho tam giác vuông ABC tại A, đường cao AH. Đường tròn đường kính BH cắt AB tại D, đường tròn đường kính CH cắt AC tại E. Chọn khẳng định sai trong các khẳng định sau

   A. DE là cát tuyến của đường tròn đường kính BH

   Đáp án chính xác

   B. DE là tiếp tuyến của đường tròn đường kính BH

   C. Tứ giác AEHD là hình chữ nhật

   D. DE ⊥ DI (với I là trung điểm BH)

   Trả lời:

   Đáp án AGọi I, J lần lượt là trung điểm của BH và CH.Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay Vì D, E lần lượt thuộc đường tròn đường kính BH và HCNên DE là tiếp tuyến của đường tròn đường kính BHTừ chứng minh trên suy ra các phương án B, C, D đúng

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====