1. Lập công thức tính khoảng cách từ gốc tọa độ đến đường thẳng.2. Áp dụng, tính khoảng cách từ gốc tọa độ đến đường thẳng 3x – 4y = 10.

Câu hỏi:

1. Lập công thức tính khoảng cách từ gốc tọa độ đến đường thẳng.2. Áp dụng, tính khoảng cách từ gốc tọa độ đến đường thẳng 3x – 4y = 10.

Trả lời:

1. Ta xét các trường hợp:Trường hợp 1: Nếu a = 0 và $\mathrm{b}\ne 0$Khi đó, đường thẳng có dạng $\mathrm{by}+\mathrm{c}=0\iff \mathrm{y}=-\frac{\mathrm{c}}{\mathrm{b}}$. Do đó, khoảng cách từ gốc O đến đường thẳng bằng $\left|-\frac{\mathrm{c}}{\mathrm{b}}\right|=\left|\frac{\mathrm{c}}{\mathrm{b}}\right|$Trường hợp 2: nếu $\mathrm{a}\ne 0$ và b = 0.Khi đó, đường thẳng có dạng$\mathrm{ax}+\mathrm{c}=0\iff \mathrm{x}=-\frac{\mathrm{c}}{\mathrm{b}}$ . Do đó, khoảng cách từ gốc O đến đường thẳng bằng $\left|-\frac{\mathrm{c}}{\mathrm{a}}\right|=\left|\frac{\mathrm{c}}{\mathrm{a}}\right|$Trường hợp 3: Nếu $\mathrm{a}\ne 0,\mathrm{b}\ne 0$Gọi A, B theo thứ tự là giao điểm của (d) với các trục Ox, Oy ta được:- Với điểm A: $\mathrm{x}=0\Rightarrow \mathrm{y}=-\frac{\mathrm{c}}{\mathrm{b}}\Rightarrow \mathrm{A}\left(0;-\frac{\mathrm{c}}{\mathrm{b}}\right)$– Với điểm B: $\mathrm{y}=0\Rightarrow \mathrm{x}=-\frac{\mathrm{c}}{\mathrm{a}}\Rightarrow \mathrm{B}\left(-\frac{\mathrm{c}}{\mathrm{a}};0\right)$Gọi H là hình chiếu vuông góc của O lên đường thẳng (d)Trong $∆\mathrm{OAB}$ vuông tại O, ta có $\frac{1}{{\mathrm{OH}}^2}=\frac{1}{{\mathrm{OA}}^2}+\frac{1}{{\mathrm{OB}}^2}$$\iff \mathrm{OH}=\frac{\mathrm{OA}.\mathrm{OB}}{\sqrt{{\mathrm{OA}}^2+{\mathrm{OB}}^2}}=\frac{\left|\frac{\mathrm{c}}{\mathrm{b}}\right|.\left|-\frac{\mathrm{c}}{\mathrm{a}}\right|}{\sqrt{{\left(\frac{\mathrm{c}}{\mathrm{b}}\right)}^2+{\left(-\frac{\mathrm{c}}{\mathrm{a}}\right)}^2}}=\frac{\left|\mathrm{c}\right|}{\sqrt{{\mathrm{a}}^2+{\mathrm{b}}^2}} \left(*\right)$2. Gọi h là khoảng cách từ O đến đường thẳng, ta có ngay $\mathrm{h}=\frac{\left|-10\right|}{\sqrt{3^2+{\left(-4\right)}^2}}=2$

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong các cặp số (-2;1); (0;2); (-1;0); (1,5;3); (4;-3) cặp số nào là nghiệm của phương trình?a) 5x + 4y = 8b) 3x + 5y = -3
   
   

   Câu hỏi:
   

   Trong các cặp số (-2;1); (0;2); (-1;0); (1,5;3); (4;-3) cặp số nào là nghiệm của phương trình?a) 5x + 4y = 8b) 3x + 5y = -3

   Trả lời:

   a. Xét phương trình 5x + 4y = 8- Với cặp số (-2;1). Ta có 5(-2) + 4.1 = -6 $\ne$8.Do đó cặp số (-2;1) không là nghiệm của phương trình.- Với cặp số (0;2). Ta có 0 + 4.2 = 8.Do đó cặp số (0;2) là nghiệm của phương trình.- Với cặp số (-1;0). Ta có (-1) + 4.0 = -5 $\ne$8.Do đó cặp số (-1;0) không là nghiệm của phương trình.- Với cặp số (1,5;3). Ta có 1,5 + 4.3 = 19,5 $\ne$8.Do đó cặp số (1,5;3) không là nghiệm của phương trình.- Với cặp số (4;-3). Ta có 4 + 4.(-3) = 8.Do đó cặp số (4;-3) là nghiệm của phương trình.b. Xét phương trình 3x + 5y = -3- Các cặp (-1;0); (4;-3) là nghiệm của phương trình.- Các cặp (-2;1); (0;2); (1,5;3) không là nghiệm của phương trình.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Giải phương trình x – 2y = 6
   
   

   Câu hỏi:
   

   Giải phương trình x – 2y = 6

   Trả lời:

   Thực hiện việc biến đổi phương trình về dạng x – 2y = 6Tới đây, cho y các giá trị tùy ý chúng ta sẽ tính được giá trị tương ứng của x, cụ thể:- Với y = -4 => x = 2.(-4) + 6 = -2 => cặp (-2;-4) là một nghiệm.- Với y = 0 => x = 2.0 + 6 = 6 => cặp (6;0) là một nghiệm.Vì y có thể lấy giá trị tùy ý, nên phương trình có vô số nghiệm, dạng tổng quát của nghiệm là $\left(\mathrm{x}=2\mathrm{y}+6;\mathrm{y}\in \mathrm{R}\right)$ hoặc viết (2y + 6; y)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Giải phương trình 0x + 2y = 12
   
   

   Câu hỏi:
   

   Giải phương trình 0x + 2y = 12

   Trả lời:

   Thực hiện việc biến đổi phương trình về dạng 2y = 12 <=> y = 6.Tới đây, cho x các giá trị tùy ý ta luôn nhận được y = 6. Do đó các cặp số (-81;6), (33;6),… đều là nghiệm của phương trình.Vậy, phương trình có vô số nghiệm, dạng tổng quát của nghiệm là $\left(\mathrm{x}\in \mathrm{R};\mathrm{y}=6\right)$ hoặc viết (x;6)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Giải phương trình 6x – 0y = 18
   
   

   Câu hỏi:
   

   Giải phương trình 6x – 0y = 18

   Trả lời:

   Thực hiện việc biến đổi phương trình về dạng 6x = 18 <=> x = 3Tới đây, cho y các giá trị tùy ý ta luôn nhận được x = 3. Do đó, các cặp số(3;2005), (3;1989),… đều là nghiệm của phương trình.Vậy phương trình có vô số nghiệm, dạng tổng quát của nghiệm là $\left(3;\mathrm{y}\in \mathrm{R}\right)$ hoặc viết (3;y)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào?
   
   

   Câu hỏi:
   

   Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào?

   Trả lời:

   Ta có- Đường thẳng biểu diễn tập nghiệm của phương trình x + 2y = 4 đi qua hai điểm A(0;2), B(4;0)- Đường thẳng biểu diễn tập nghiệm của phương trình x – y = 1 đi qua hai điểm C(0;-1), D(1;0)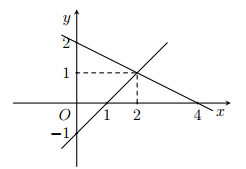Từ đồ thị hàm số, dễ dàng nhận thấy hai đường thẳng AB và CD giao nhau tại điểm M (2;1)Vì $\mathrm{M}\in \mathrm{AB}, \mathrm{M}\in \mathrm{CD}$ nên tọa độ M là nghiệm của cả hai phương trình x + 2y = 4 và x – y = 1.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====