Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

Câu hỏi:

Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

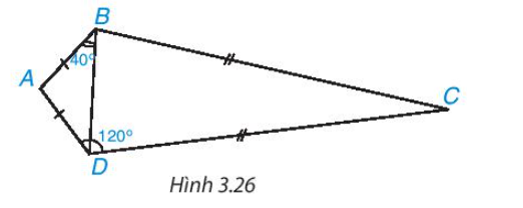
Trả lời:

* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• $\widehat{ABD}=\widehat{ADB}=40°$.
• $\widehat{A}+\widehat{ABD}+\widehat{ADB}=180°$.
Suy ra $\widehat{A}=180°-\widehat{ABD}-\widehat{ADB}=180°-40°-40°=100°$.
Ta có $\widehat{ADB}+\widehat{BDC}=120°$ suy ra $\widehat{BDC}=120°-\widehat{ADB}=120°-40°=80°$.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• $\widehat{CBD}=\widehat{CDB}=80°$.
• $\widehat{C}+\widehat{CBD}+\widehat{CDB}=180°$
Suy ra $\widehat{C}=180°-\widehat{CBD}-\widehat{CDB}=180°-80°-80°=20°$.
Ta có: $\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=40°+80°=120°$.
Vậy số đo các góc của tứ giác ABCD là $\widehat{A}=100°; \widehat{ABC}=120° ;\widehat{C}=20°$.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?
   
   

   Câu hỏi:
   

   Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?
   

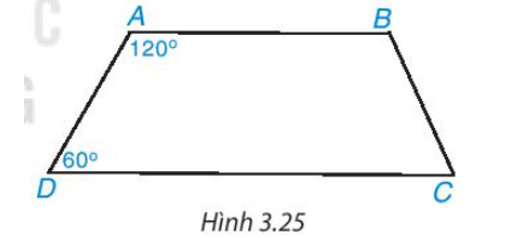
   Trả lời:

   
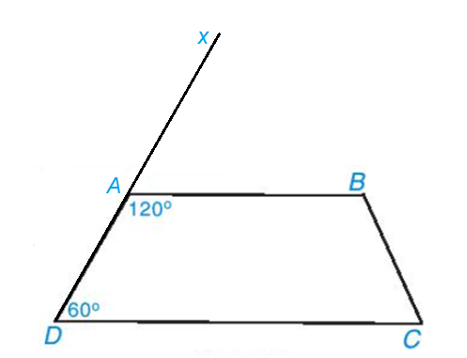
   Vẽ tia Dx đi qua điểm A.
   Vì $\widehat{DAB}$ và $\widehat{BAx}$ là hai góc kề bù nên $\widehat{DAB}+\widehat{BAx}=180°$.
   Suy ra $\widehat{BAx}=180°-\widehat{DAB}=180°-120°=60°$.
   Ta có $\widehat{ADC}=\widehat{BAx}=60°$ mà hai góc này ở vị trí đồng vị nên AB // CD.
   Vậy tứ giác ABCD là hình thang.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết ABD^=30°, tính số đo các góc của hình thang đó.
   
   

   Câu hỏi:
   

   Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết $\widehat{ABD}=30°$, tính số đo các góc của hình thang đó.

   Trả lời:

   
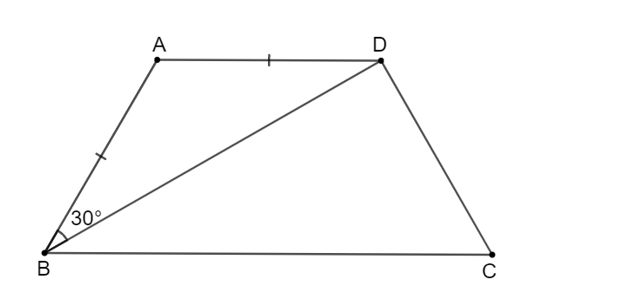
   Xét tam giác ABD cân tại A (vì AB = AD), ta có:
   • $\widehat{ABD}=\widehat{ADB}=30°$
   • $\widehat{A}+\widehat{ABD}+\widehat{ADB}=180°$ hay $\widehat{A}+30°+30°=180°$
   Suy ra $\widehat{A}=180°-30°-30°=120°$.
   Vì AB // CD nên $\widehat{ADB}=\widehat{CBD}=30°$ (hai góc so le trong).
   Do đó $\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=30°+30°=60°$.
   Vì tứ giác ABCD là hình thang cân nên $\widehat{ABC}=\widehat{C}=60°$.
   Ta có: $\widehat{A}+\widehat{ABC}+\widehat{C}+\widehat{ADC}=360°$.
   $120°+60°+60°+\widehat{ADC}=360°$
   $240°+\widehat{ADC}=360°$
   Suy ra $\widehat{ADC}=360°-240°=120°$.

   Vậy số đo các góc của hình thang ABCD là $\widehat{A}=120°; \widehat{ABC}=60°; \widehat{ABC}=60°; \widehat{ADC}=120°.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R. a) Chứng minh tứ giác APMR là hình thang cân.
   
   

   Câu hỏi:
   

   Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
   a) Chứng minh tứ giác APMR là hình thang cân.

   Trả lời:

   
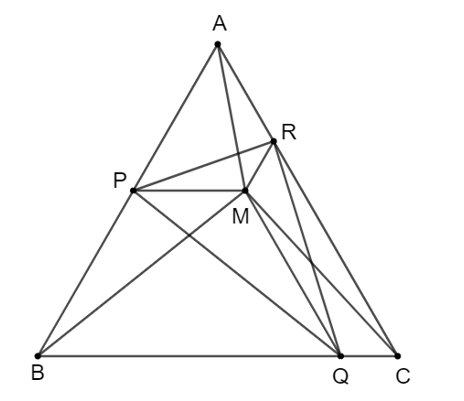
   a) Vì tam giác ABC đều nên $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60°$.
   Vì PM // BC nên $\widehat{ABC}=\widehat{APM}=60°$.
   Tứ giác APMR là hình thang (vì MR // AP) có $\widehat{ABC}=\widehat{APM}$.
   Do đó tứ giác APMR là hình thang cân.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
   
   

   Câu hỏi:
   

   b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

   Trả lời:

   b) Vì tứ giác APMR là hình thang cân nên AM = PR        (1)
   Vì MQ // AC nên $\widehat{BQM}=\widehat{ACB}=60°$.
   Tứ giác BPMQ là hình thang (vì PM // BQ) có $\widehat{BQM}=\widehat{ACB}$ nên BPMQ là hình thang cân.
   Suy ra BM = PQ    (2)
   Chứng minh tương tự, ta có MC = QR          (3)
   Từ (1); (2) và (3) suy ra PR + BM + QR = MA + MB + MC.
   Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?
   
   

   Câu hỏi:
   

   c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

   Trả lời:

   c) Vì chu vi tam giác PQR bằng tổng độ dài MA + MB + MC
   Để tam giác PQR là tam giác đều thì PQ = QR = PR suy ra MA = MB = MC
   Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.
   Do đó M là giao điểm của ba đường trung trực (đồng thời M cũng là giao điểm của ba đường trung tuyến, ba đường cao, đường phân giác).
   Vậy khi M là giao điểm của ba đường trung trực thì tam giác PQR là tam giác đều.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====