Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh: a) ΔIAM = ΔICN;

By 0

Câu hỏi:

Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh:
a) ΔIAM = ΔICN;

Trả lời:

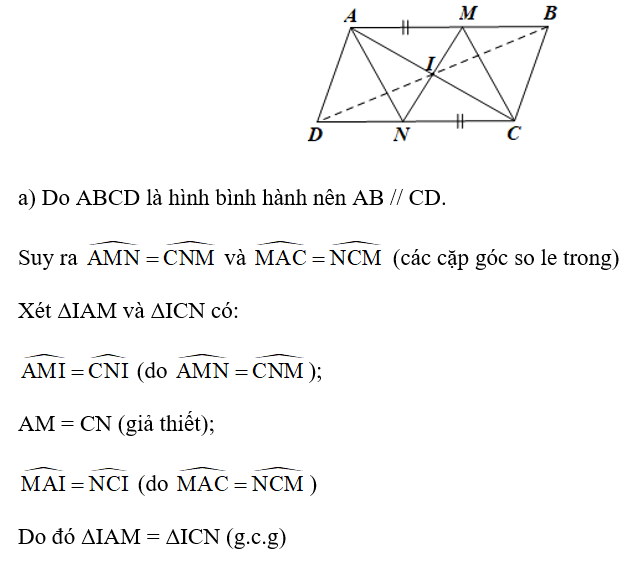
Cho hình bình hành ABCD. Gọi M là điểm nằm giữa A và B, N là điểm nằm giữa C và D sao cho AM = CN. Gọi I là giao điểm của MN và AC. Chứng minh: a) ΔIAM = ΔICN; (ảnh 1)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

  1. Cho tứ giác ABCD có A^=60°,B^=70°,C^=80°. Khi đó, D^ bằng A. 130°. B. 140°. C. 150°. D. 160°.

    Câu hỏi:

    Cho tứ giác ABCD có A^=60°,B^=70°,C^=80°. Khi đó, D^ bằng
    A. 130°.
    B. 140°.
    C. 150°.
    D. 160°.

    Trả lời:

    Đáp án đúng là: C
    Theo định lí tổng các góc của một tứ giác ta có: A^+B^+C^+D^=360°.
    Suy ra D^=360°−A^−B^−C^=360°−60°−70°−80°=150°.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  2. Cho hình thang cân ABCD có AB // CD, A^=80°. Khi đó, C^ bằng A. 80°. B. 90°. C. 100°. D. 110°.

    Câu hỏi:

    Cho hình thang cân ABCD có AB // CD, A^=80°. Khi đó, C^ bằng
    A. 80°.
    B. 90°.
    C. 100°.
    D. 110°.

    Trả lời:

    Đáp án đúng là: C
    Cho hình thang cân ABCD có AB // CD, góc A = 80 độ . Khi đó, góc C độ bằng A. 80°. B. 90°. C. 100°. D. 110°. (ảnh 1)

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  3. Cho hình bình hành MNPQ có các góc khác 90°, MP cắt NQ tại I. Khi đó A. IM = IN. B. IM = IP. C. IM = IQ. D. IM = MP.

    Câu hỏi:

    Cho hình bình hành MNPQ có các góc khác 90°, MP cắt NQ tại I. Khi đó
    A. IM = IN.
    B. IM = IP.
    C. IM = IQ.
    D. IM = MP.

    Trả lời:

    Đáp án đúng là: B
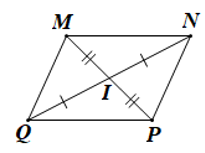
    Cho hình bình hành MNPQ có các góc khác 90°, MP cắt NQ tại I. Khi đó A. IM = IN. B. IM = IP. C. IM = IQ. D. IM = MP. (ảnh 1)

    Hình bình hành MNPQ có hai đường chéo MP cắt NQ tại I nên I là trung điểm của mỗi đường.
    Do I là trung điểm của MP nên IM = IP.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

  4. Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây? A. NQ. B. MN. C. NP. D. QM.

    Câu hỏi:

    Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây?
    A. NQ.
    B. MN.
    C. NP.
    D. QM.

    Trả lời:

    Đáp án đúng là: A
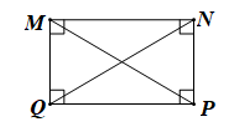
    Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây? A. NQ. B. MN. C. NP. D. QM. (ảnh 1)

    Do MNPQ là hình chữ nhật nên MP = NQ (hai đường chéo bằng nhau).

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

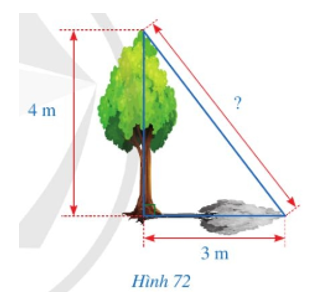
  5. Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh 4 m của cây.

    Câu hỏi:

    Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh 4 m của cây.
    Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh 4 m của cây. (ảnh 1)

    Trả lời:

    Giả sử Hình 72 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình vẽ dưới đây:
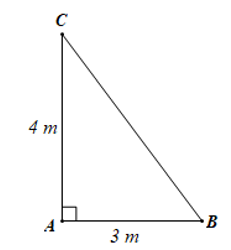
    Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh 4 m của cây. (ảnh 2)

    Yêu cầu bài toán trở thành tìm độ dài cạnh BC.
    Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:
    BC2 = AB2 + AC2 = 32 + 42 = 25
    Do đó BC = 5 (m).
    Vậy khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là 5 m.

    ====== **** mời các bạn xem câu tiếp bên dưới **** =====

Bài liên quan:

Leave a Comment

Back to Top
Menu