Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.

Câu hỏi:

Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.

Trả lời:

Hình thang ABCD có AB // CDM là trung điểm của AD (gt)N là trung điểm của BC (gt)Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CDMN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)* Trong tam giác ADC, ta có:M là trung điểm của ADMK // CD⇒ AK= KC và MK là đường trung bình của $∆$ADC.⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)Vậy: KN = MN – MK = 10 – 7 = 3 (cm)* Trong $∆$ADB, ta có:M là trung điểm của ADMI // AB nên DI = IB⇒ MI là đường trung bình của $∆$DAB⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)IK = MK – Ml = 7 – 3 = 4 (cm)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4( cm ). Tính độ dài MN.
   
   

   Câu hỏi:
   

   Cho Δ ABC có M là trung điểm của AB, N là trung điểm của AC và BC = 4( cm ). Tính độ dài MN.

   Trả lời:

   Theo giả thiết ta có M là trung điểm của AB, N là trung điểm của AC⇒ MN là đường trung bình của Δ ABC.Áp dụng định lý 2, ta có MN = 1/2BC.⇒ MN = 1/2BC = 1/2.4 = 2( cm )

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC và AB = 4( cm ) và CD = 7( cm ). Tính độ dài đoạn EF.
   
   

   Câu hỏi:
   

   Cho hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC và AB = 4( cm ) và CD = 7( cm ). Tính độ dài đoạn EF.

   Trả lời:

   Ta có hình thang ABCD có E là trung điểm của AD, F là trung điểm của BC⇒ EF là đường trung bình của hình thang.Áp dụng định lý 2, ta có EF = (AB + CD)/2⇒ EF = (AB + CD)/2 = (4 + 7)/2 = 5,5( cm ).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC( AB > AC ) có A^=500. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD,BC. Tính BEF ^= ?
   
   

   Câu hỏi:
   

   Cho tam giác ABC( AB > AC ) có $\hat{A}={50}^0$. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E,F lần lượt là trung điểm của cạnh AD,BC. Tính $\widehat{BEF }=$ ?

   Trả lời:

   Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác ACD và BCD.Đặt BD = AC = 2aÁp dụng định lý đường trung bình của hai tam giác trên ta có:( 1 )      FI//BD       ( 2 )       FI = a( 3 )      EI = a       ( 4 )      EI//AC

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hình thang ABCD ( AB//CD ) có AB = 2cm,CD = 5cm,AD = 7cm. Gọi E là trung điểm của BC. Tính AED^= ?
   
   

   Câu hỏi:
   

   Cho hình thang ABCD ( AB//CD ) có AB = 2cm,CD = 5cm,AD = 7cm. Gọi E là trung điểm của BC. Tính $\widehat{AED}= ?$

   Trả lời:

   Ta có EI là đường trung bình của hình thang ABCD.Áp dụng định lý đường trung bình của hình thang ABCD ta có:IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm )       ( 2 )Từ ( 1 ) và ( 2 ) ta có (vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)+ Xét tam giác ADE có

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
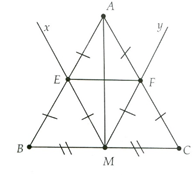
5. Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:a) EF là đường trung bình của tam giác ABC;b) AM là đường trung trực của EF.
   
   

   Câu hỏi:
   

   Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tia Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh:a) EF là đường trung bình của tam giác ABC;b) AM là đường trung trực của EF.

   Trả lời:

   a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====