b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Câu hỏi:

b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Trả lời:

b) Vì hình bình hành AEFD có hai đường chéo AF và DE nên chúng cắt nhau tại trung điểm của mỗi đường, ta gọi giao điểm đó là O.
Hình bình hành AEFD có hai đường chéo AF và BC.
Mà O là trung điểm của AF.
Suy ra O cũng là trung điểm của BC.
Vậy các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

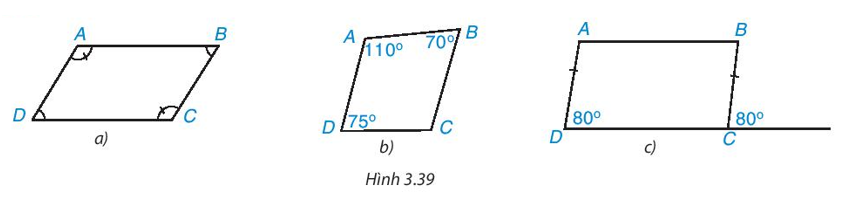
1. Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
   
   

   Câu hỏi:
   

   Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?
   

   Trả lời:

   * Hình 3.36a)
   Tứ giác ABCD có: $\widehat{A}=\widehat{C}=100°; \widehat{B}=\widehat{D}=80°$.
   Do đó, tứ giác ABCD là hình bình hành.
   * Hình 3.36b)
   Tứ giác ABCD có: $\widehat{B}\ne \widehat{D}(70°\ne 75°)$.
   Do đó, tứ giác ABCD không là hình bình hành.
   * Hình 3.36c)
   Đặt $\widehat{BCx}=80°$ (như hình vẽ
   
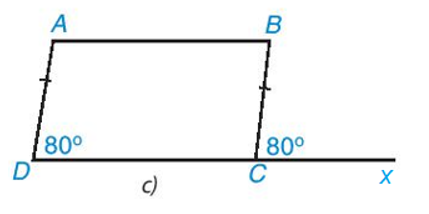
   Ta có: $\widehat{D}=\widehat{BCx}=80°$ mà hai góc này ở vị trí đồng vị nên AD // BC.
    
   Tứ giác ABCD có:
   • AD // BC (chứng minh trên)
   • AD = BC (giả thiết)
   Do đó, tứ giác ABCD là hình bình hành.
   Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng: a) AN = CM;
   
   

   Câu hỏi:
   

   Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:
   a) AN = CM;

   Trả lời:

   
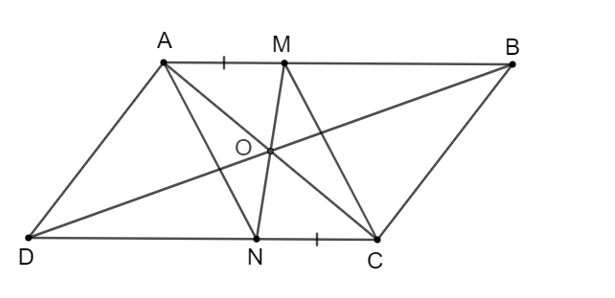
   a) Vì ABCD là hình bình hành nên AB // CD.
   Tứ giác AMCN có AM // CD (vì AB // CD); AM = CN (giả thiết).
   Suy ra, tứ giác AMCN là hình bình hành.
   Do đó AN = CM (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. b) AMC^=ANC^
   
   

   Câu hỏi:
   

   b) $\widehat{AMC}=\widehat{ANC}$

   Trả lời:

   b) Vì tứ giác AMCN là hình bình hành suy ra $\widehat{AMC}=\widehat{ANC}$ (đpcm).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Vẽ tứ giác ABCD theo hướng dẫn sau: Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB. Bước 2. Lấy điểm C ∈ a. Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC. Hãy giải thích tại sao tứ giác ABCD là hình bình hành.
   
   

   Câu hỏi:
   

   Vẽ tứ giác ABCD theo hướng dẫn sau:
   Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.
   Bước 2. Lấy điểm C ∈ a.
   Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.
   Hãy giải thích tại sao tứ giác ABCD là hình bình hành.

   Trả lời:

   Ta thực hiện vẽ tứ giác ABCD theo các bước ở đề bài như sau:
   Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB
   
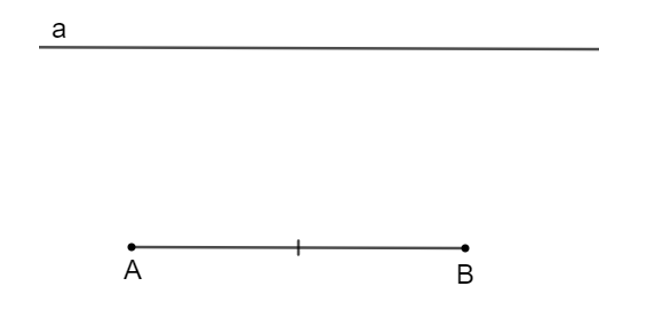
   Bước 2. Lấy điểm C ∈ a
   
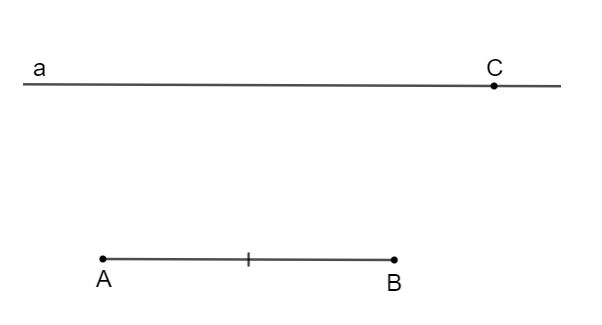
   Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC
   
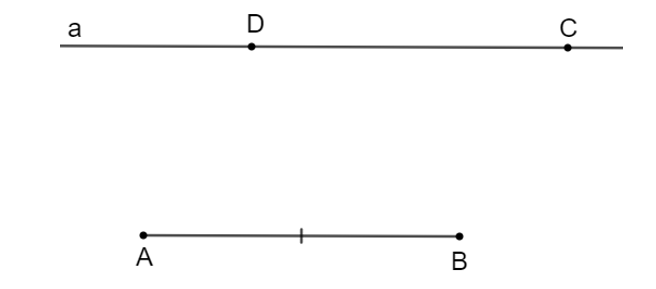
   Nối AD, BC ta có tứ giác ABCD là hình bình hành
   
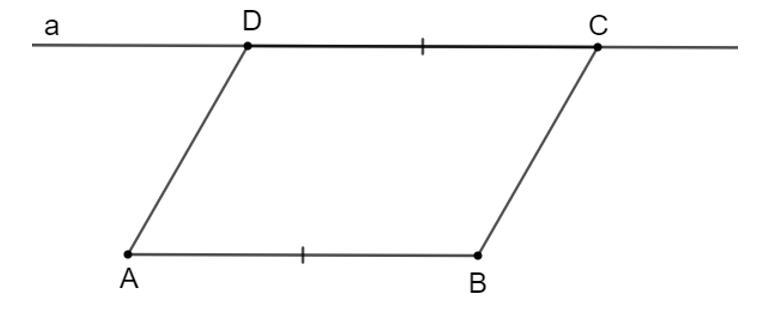
   Tứ giác ABCD là hình bình hành do:
   • AB // CD (vì AB // a; C, D ∈ a);
   • AB = CD (giả thiết).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm. a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
   
   

   Câu hỏi:
   

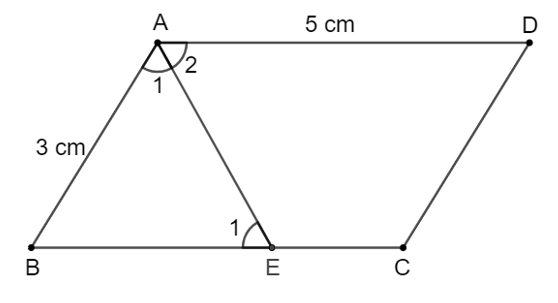
   Cho hình bình hành ABCD có AB = 3 cm, AD = 5 cm.
   a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?

   Trả lời:

   a) Vì AD > AB (5 cm > 3 cm) nên tia phân giác của góc A cắt cạnh CD
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====