[Năm 2022] Bộ 11 Đề thi Giữa kì 1 Toán lớp 8 có đáp án

[Năm 2022] Đề thi Giữa kì 1 Toán lớp 8 có đáp án (11 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 1

Câu 1. Phân tích các đa thức sau thành nhân tử

a. ${\text{3xy – 9x}}^{\text{2}}$

b. ${\text{x}}^{\text{3}}\text{+ 343}$

c. ${\text{25 – x}}^{\text{2}}{\text{+ 2xy – y}}^{\text{2}}$ 

Câu 2. Thực hiện phép tính rồi tính giá trị biểu thức: $\left(\frac{\text{3}}{\text{4}}{\text{x}}^{\text{4}}{\text{y}}^{\text{2}}\text{– }\frac{\text{9}}{\text{2}}{\text{x}}^{\text{3}}{\text{y}}^{\text{2}}{\text{+ 9x}}^{\text{2}}{\text{y}}^{\text{2}}{\text{– 6xy}}^{\text{2}}\right):\left(\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}\right)$

 tại x = 1 và y = 2020

Câu 3. Tìm x biết:

a.  $\text{3}{\left(\text{x – 1}\right)}^{\text{2}}\text{+ }\left(\text{x + 5}\right)\left(\text{2 – 3x}\right)\text{ = -25}$

b. ${\left(\text{x – 2}\right)}^{\text{2}}\text{– 4x + 8 = 0}$ 

Câu 4. Cho tam giác ABC nhọn, các đường cao AD và BE cắt nhau tại H. Gọi M là trung điểm của BC. Điểm P đối xứng với điểm H qua đường thẳng BC. Điểm Q đối xứng với điểm H qua điểm M.

a. Chứng minh PQ // BC. Khi đó tứ giác DMQP là hình gì? Vì sao?

b. Chứng minh tứ giác HCQB là hình bình hành. Tính số đo các góc $\widehat{\text{ACQ}}\text{,}\widehat{\text{ABQ}}$ .

c. Gọi O là giao điểm các đường trung trực của . Chứng minh rằng điểm O cách đều 5 điểm A, B, P, Q, C.

Câu 5. Tìm giá trị nhỏ nhất của biểu thức:

 $\text{P = }{\left({\text{x}}^{\text{2}}\text{+ 4x + 1}\right)}^{\text{2}}\text{– 12}{\left(\text{x + 2}\right)}^{\text{2}}\text{+ 2093}$

ĐÁP ÁN

Câu 1. Phân tích các đa thức sau thành nhân tử

a. ${\text{3xy – 9x}}^{\text{2}}$                    b.${\text{x}}^{\text{3}}\text{+ 343}$                       c. ${\text{25 – x}}^{\text{2}}{\text{+ 2xy – y}}^{\text{2}}$ 

Lời giải

a. ${\text{3xy – 9x}}^{\text{2}}=\text{3x}\left(\text{y – 3x}\right)$                            

b. ${\text{x}}^{\text{3}}{\text{+ 343= x}}^{\text{3}}{\text{+ 7}}^{\text{3}}\text{= }\left(\text{x + 7}\right)\left({\text{x}}^{\text{2}}\text{– 7x + 49}\right)$                     

c. ${\text{25 – x}}^{\text{2}}{\text{+ 2xy – y}}^{\text{2}}\text{= 25 – }{\left(\text{x – y}\right)}^{\text{2}}\text{= }\left(\text{5 + x – y}\right)\left(\text{5 – x + y}\right)$  

Câu 2. Thực hiện phép tính rồi tính giá trị biểu thức: $\left(\frac{\text{3}}{\text{4}}{\text{x}}^{\text{4}}{\text{y}}^{\text{2}}\text{– }\frac{\text{9}}{\text{2}}{\text{x}}^{\text{3}}{\text{y}}^{\text{2}}{\text{+ 9x}}^{\text{2}}{\text{y}}^{\text{2}}{\text{– 6xy}}^{\text{2}}\right):\left(\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}\right)$

 tại x = 1 và y = 2020

Lời giải

$\text{A = }\frac{\text{3}}{\text{4}}{\text{x}}^{\text{4}}{\text{y}}^{\text{2}}\text{: }\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}\text{– }\frac{\text{9}}{\text{2}}{\text{x}}^{\text{3}}{\text{y}}^{\text{2}}\text{: }\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}{\text{+ 9x}}^{\text{2}}{\text{y}}^{\text{2}}\text{: }\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}{\text{– 6xy}}^{\text{2}}:\frac{\text{3}}{\text{4}}{\text{xy}}^{\text{2}}$ 

$\iff {\text{A = x}}^{\text{3}}{\text{– 6x}}^{\text{2}}\text{+ 12x – 8}$

Với x = 1;  y = 2020 ta có $\iff {\text{A = 1}}^{\text{3}}{\text{– 6.1}}^{\text{2}}\text{+ 12.1 – 8 = -1}$

Câu 3. Tìm x biết:

a.  $\text{3}{\left(\text{x – 1}\right)}^{\text{2}}\text{+ }\left(\text{x + 5}\right)\left(\text{2 – 3x}\right)\text{ = -25}$

b.  ${\left(\text{x – 2}\right)}^{\text{2}}\text{– 4x + 8 = 0}$

Lời giải

a.  $\text{3}{\left(\text{x – 1}\right)}^{\text{2}}\text{+ }\left(\text{x + 5}\right)\left(\text{2 – 3x}\right)\text{ = -25}$

 $\iff {\text{3x}}^{\text{2}}{\text{– 6x + 3 – 3x}}^{\text{2}}\text{– 13x + 10 + 25 = 0}$

 $\iff \text{-19x + 38 = 0 }\iff \text{x = 2}$

Vậy x = 2.

b.  ${\left(\text{x – 2}\right)}^{\text{2}}\text{– 4x + 8 = 0}$

$\iff \left(\text{x – 2}\right)\text{.}\left(\text{x – 2 – 4}\right)\text{ = 0}$ 

$\iff \left(\text{x – 2}\right)\text{.}\left(\text{x – 6}\right)\text{ = 0}$ 

$\iff \left[\begin{array}{c}\text{x – 2 = 0}\\ \text{x – 6 = 0}\end{array}\right.\iff \left[\begin{array}{c}\text{x = 2}\\ \text{x = 6}\end{array}\right.$

Vậy  $\text{x}\in \left\{2;6\right\}$

Câu 4. Cho tam giác ABC nhọn, các đường cao AD và BE cắt nhau tại H. Gọi M là trung điểm của BC. Điểm P đối xứng với điểm H qua đường thẳng BC. Điểm Q đối xứng với điểm H qua điểm M.

a. Chứng minh PQ // BC. Khi đó tứ giác DMQP là hình gì? Vì sao?

b. Chứng minh tứ giác HCQB là hình bình hành. Tính số đo các góc $\widehat{\text{ACQ}}\text{,}\widehat{\text{ABQ}}$ .

c. Gọi O là giao điểm các đường trung trực của $△\text{ABC}$. Chứng minh rằng điểm O cách đều 5 điểm A, B, P, Q, C.

Lời giải

a. Chứng minh PQ // BC. Khi đó tứ giác DMQP là hình gì? Vì sao?

Có P đối xứng với H qua BC

Nên BC là trung trực của PH.

$\Rightarrow \text{BC}\perp \text{PH}$ tại D và D là trung điểm của PH

Có điểm Q đối xứng với điểm H qua điểm M nên M là trung điểm của QH.

Xét $\Delta \text{HPQ}$ có D là trung điểm của PH; M là trung điểm của QH

Nên MD là đường trung bình của $\Delta \text{HPQ}$

DM // PQ hay PQ // BC

Tứ giác DMQP có DM // PQ

Nên tứ giác DMQP là hình thang (DM // PQ)

Mà $\widehat{\text{PDM}}=90°$ ( do $\text{BC}\perp \text{PH}$ tại D)

Vậy tứ giác DMQP là hình thang vuông (DM // PQ)

b. Chứng minh tứ giác HCQB là hình bình hành. Tính số đo các góc $\widehat{\text{ACQ}}\text{,}\widehat{\text{ABQ}}$

Xét tứ giác HCQB có HQ và BC cắt nhau tại M là trung điểm của mỗi đường.

 Tứ giác HCQB là hình bình hành.

$\Rightarrow \left\{\begin{array}{c}\text{QC // BH}\\ \\ \text{QB // CH}\end{array}\right.$ 

Mà  $\left\{\begin{array}{c}\text{BH }\perp \text{AC}\\ \text{CH}\perp \text{AB}\end{array}\right.$

Nên  $\left\{\begin{array}{c}\text{QC}\perp \text{AC}\\ \text{QB}\perp \text{AB}\end{array}\right.\Rightarrow \left\{\begin{array}{c}\widehat{\text{ACQ}}=90°\\ \widehat{\text{ABQ}}=90°\end{array}\right.$

c. Gọi O là giao điểm các đường trung trực của $△\text{ABC}$. Chứng minh rằng điểm O cách đều 5 điểm A, B, P, Q, C.

gọi O’ là trung điểm của AQ

có $\Delta \text{ABQ}$ vuông tại B (do $\widehat{\text{ABQ}}=90°$)

có BO’ là trung tuyến

Nên  $\text{BO’ = }\frac{\text{1}}{\text{2}}\text{AQ}$

Chứng minh tương tự ta có: $\text{CO’ = }\frac{\text{1}}{\text{2}}\text{AQ}$

Mà $\text{AO’ = O’Q = }\frac{\text{1}}{\text{2}}\text{AQ}$ (do O’ là trung điểm của AQ)

 $\Rightarrow \text{AO’ = BO’ = CO’}$

 $\Rightarrow \text{O’}\equiv \text{O}$

Có PQ // BC;  $\text{BC}\perp \text{AP}\Rightarrow \text{PQ}\perp \text{AP}$

$\Rightarrow \widehat{\text{APQ}}=90°$ 

$\Rightarrow \Delta \text{APQ}$ vuông tại P

Có PO là trung tuyến

Nên  $\text{PO = }\frac{\text{1}}{\text{2}}\text{AQ}$

$\Rightarrow \text{OA = OB = OC = OQ }\left(=\frac{1}{2}\text{AQ}\right)$ 

Vậy điểm O cách đều 5 điểm A, B, P, Q, C.

Câu 5. Tìm giá trj nhỏ nhất của biểu thức:

 $\text{P = }{\left({\text{x}}^{\text{2}}\text{+ 4x + 1}\right)}^{\text{2}}\text{– 12}{\left(\text{x + 2}\right)}^{\text{2}}\text{+ 2093}$

Lời giải

Ta có: $\text{P = }{\left({\text{x}}^{\text{2}}\text{+ 4x + 1}\right)}^{\text{2}}\text{– 12}{\left(\text{x + 2}\right)}^{\text{2}}\text{+ 2093}$.

$\Rightarrow \text{P = }{\left({\text{x}}^{\text{2}}\text{+ 4x + 1}\right)}^{\text{2}}\text{– 12}\left({\text{x}}^2\text{ + 4x + 4}\right)\text{+ 2093}$

 Đặt t = ${\text{x}}^{\text{2}}\text{+ 4x + 1}$

 $\Rightarrow {\text{P = t}}^{\text{2}}\text{– 12}\left(\text{t + 3}\right)\text{ + 2093}$

 $\Rightarrow {\text{P = t}}^{\text{2}}\text{– 12t – 36 + 2093}$

 $\Rightarrow \text{P = }\left({\text{t}}^{\text{2}}\text{– 2.6.t + 36}\right)\text{ + 2021}$

$\Rightarrow \text{P = }{\left(\text{t – 6}\right)}^{\text{2}}\text{+ 2021}\ge \text{2021}$

Dấu “=” xảy ra khi và chỉ khi  $\text{t – 6 = 0}\Rightarrow \left[\begin{array}{c}\text{x = 1}\\ \text{x = 5}\end{array}\right.$

Vậy giá trị nhỏ nhất của P bằng 2021 đạt được khi x = 1 hoặc x = 5.

…………………………………………………………………………………

[Năm 2022] Đề thi Giữa kì 1 Toán lớp 8 có đáp án (11 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 2

 

Đề 2:

Bài 1. (2 điểm) Rút gọn biểu thức:

a. $\text{x}\left(\text{x + 2}\right)\text{ – 2x}$                                         

b. $\left(\text{2 + x}\right)\left(\text{2 – x}\right){\text{ + x}}^{\text{2}}$ 

c. ${\text{x}}^{\text{2}}\left(\text{1 – x}\right)\text{ + }\left(\text{x + 3}\right)\left({\text{x}}^{\text{2}}\text{– 3x + 9}\right)$               

d. ${\left(\text{2x + y}\right)}^{\text{2}}{\text{+ 4x}}^{\text{2}}\text{– 4x}\left(\text{2x + y}\right)$  

Bài 2 (2,0 điểm) Phân tích đa thức thành nhân tử:

a. $\text{5xy – 10}$                                                   b. ${\text{x}}^{\text{2}}\text{– 36}$ 

c. ${\text{x}}^{\text{3}}{\text{– x}}^{\text{2}}\text{y + 4x – 4y}$                                      d. ${\text{x}}^{\text{2}}{\text{+ 12y – y}}^{\text{2}}\text{– 36}$  

Bài 3. (2,0 điểm) Tìm x biết:

a. $\text{3}\left(\text{x + 1}\right)\text{ + 5x = 0}$                                   

b. ${\text{x}}^{\text{2}}\text{– 5x = 0}$  

c. ${\text{4x}}^{\text{2}}\text{– 1 – }\left(\text{2x + 1}\right)\text{ = 0}$                                

d. ${\text{x}}^{\text{2}}\text{– 7x + 10 = 0}$  

Bài 4 (3,5 điểm) Cho tam giác ABC cân tại A $\left(\widehat{\text{A}}<90°\right)$. Gọi M, N lần lượt là trung điểm của AB và Ac.

a. Tính MN biết BC = 7 cm.

b. Chứng minh rằng tứ giác MNCB là hình thang cân.

c. Kẻ MI vuông góc với BN tại I, $\left(\text{I}\in \text{BN}\right)$ và CK vuông góc với BN tại K $\left(\text{K}\in \text{BN}\right)$. Chứng minh rằng: CK = 2MI.

d. Kẻ BD vuông góc với MC tại D $\left(\text{D}\in \text{MC}\right)$. Chứng minh rằng DK // BC.

Bài 5. (0,5 điểm) Tìm giá trị lớn nhất của biểu thức:   ${\text{A = 7 – x}}^{\text{2}}\text{– 3x}$

ĐÁP ÁN KIỂM TRA GIỮA KỲ

Bài 1. (2 điểm) Rút gọn biểu thức:

a. $\text{x}\left(\text{x + 2}\right)\text{ – 2x}$                                         

b.  $\left(\text{2 + x}\right)\left(\text{2 – x}\right){\text{ + x}}^{\text{2}}$

c. ${\text{x}}^{\text{2}}\left(\text{1 – x}\right)\text{ + }\left(\text{x + 3}\right)\left({\text{x}}^{\text{2}}\text{– 3x + 9}\right)$               

d.  ${\left(\text{2x + y}\right)}^{\text{2}}{\text{+ 4x}}^{\text{2}}\text{– 4x}\left(\text{2x + y}\right)$

Lời giải

a. $\text{x}\left(\text{x + 2}\right)\text{ – 2x}$   

${\text{= x}}^{\text{2}}\text{+ 2x – 2x}$ 

 $={\text{x}}^2$                             

b.  $\left(\text{2 + x}\right)\left(\text{2 – x}\right){\text{ + x}}^{\text{2}}$

${\text{= 4 – x}}^{\text{2}}{\text{+ x}}^{\text{2}}$ 

= 4

c.      ${\text{x}}^{\text{2}}\left(\text{1 – x}\right)\text{ + }\left(\text{x + 3}\right)\left({\text{x}}^{\text{2}}\text{– 3x + 9}\right)$

${\text{= x}}^{\text{2}}{\text{– x}}^{\text{3}}{\text{+ x}}^{\text{3}}\text{+ 27}$ 

 

d.  ${\left(\text{2x + y}\right)}^{\text{2}}{\text{+ 4x}}^{\text{2}}\text{– 4x}\left(\text{2x + y}\right)$

$={\left(\text{2x + y – 2x}\right)}^2$ 

$={\text{y}}^2$ 

Bài 2 (2,0 điểm) Phân tích đa thức thành nhân tử:

a. $\text{5xy – 10}$                                                  

b. ${\text{x}}^{\text{2}}\text{– 36}$  

c. ${\text{x}}^{\text{3}}{\text{– x}}^{\text{2}}\text{y + 4x – 4y}$                                    

d. ${\text{x}}^{\text{2}}{\text{+ 12y – y}}^{\text{2}}\text{– 36}$ 

Lời giải

a. $\text{5xy – 10 = 5}\left(\text{xy – 2}\right)$                                                   

b. ${\text{x}}^{\text{2}}\text{– 36 = }\left(\text{x + 6}\right)\left(\text{x – 6}\right)$ 

c. ${\text{x}}^{\text{3}}{\text{– x}}^{\text{2}}{\text{y + 4x – 4y = x}}^2\left(\text{x – y}\right)+4\left(\text{x – y}\right)=\left(\text{x – y}\right)\left({\text{x}}^2+4\right)$                                    

d. ${\text{x}}^{\text{2}}{\text{+ 12y – y}}^{\text{2}}{\text{– 36 = x}}^2\text{– }\left({\text{y}}^{\text{2}}\text{– 12y + 36}\right){\text{ = x}}^{\text{2}}\text{– }{\left(\text{y – 6}\right)}^{\text{2}}\text{= }\left(\text{x + y – 6}\right)\left(\text{x – y + 6}\right)$ 

Bài 3. (2,0 điểm) Tìm x biết:

a. $\text{3}\left(\text{x + 1}\right)\text{ + 5x = 0}$                                    b. ${\text{x}}^{\text{2}}\text{– 5x = 0}$ 

c. ${\text{4x}}^{\text{2}}\text{– 1 – }\left(\text{2x + 1}\right)\text{ = 0}$                                d. ${\text{x}}^{\text{2}}\text{– 7x + 10 = 0}$ 

Lời giải

a. $\text{3}\left(\text{x + 1}\right)\text{ + 5x = 0}\iff \text{8x = -3}\iff \text{x = –}\frac{3}{8}$                                   

b.  ${\text{x}}^{\text{2}}\text{– 5x = 0}\iff \text{x }\left(\text{x – 5}\right)=0\iff \left[\begin{array}{c}\text{x = 0}\\ \text{x = 5}\end{array}\right.$

Vậy  $\text{x}\in \left\{0;5\right\}$

c.   ${\text{4x}}^{\text{2}}\text{– 1 – }\left(\text{2x + 1}\right)\text{ = 0}$

$\iff \left(\text{2x – 1}\right)\left(\text{2x + 1}\right)\text{ – }\left(\text{2x + 1}\right)\text{ = 0}$ 

$\iff \left(\text{2x + 1}\right)\left(\text{2x – 2}\right)\text{ = 0}$ 

$\iff \left[\begin{array}{c}\text{2x +1 = 0}\\ \text{2x -2 = 0}\end{array}\right.\iff \left[\begin{array}{c}\text{x = – }\frac{1}{2}\\ \text{x = 1}\end{array}\right.$ 

Vậy  $\text{x}\in \left\{\text{–}\frac{1}{2};1\right\}$               

d. ${\text{x}}^{\text{2}}\text{– 7x + 10 = 0}$

$\iff {\text{x}}^{\text{2}}\text{– 2x – 5x + 10 = 0}$ 

 $\iff \text{x}\left(\text{x – 2}\right)\text{ – 5}\left(\text{x – 2}\right)\text{ = 0}$

$\iff \left(\text{x – 2}\right)\left(\text{x – 5}\right)\text{ = 0}\iff \left[\begin{array}{c}\text{x = 2}\\ \text{x = 5}\end{array}\right.$

Vậy  $\text{x}\in \left\{2;5\right\}$

Bài 4 (3,5 điểm) Cho tam giác ABC cân tại A $\left(\widehat{\text{A}}<90°\right)$. Gọi M, N lần lượt là trung điểm của AB và Ac.

a. Tính MN biết BC = 7 cm.

b. Chứng minh rằng tứ giác MNCB là hình thang cân.

c. Kẻ MI vuông góc với BN tại I, $\left(\text{I}\in \text{BN}\right)$ và CK vuông góc với BN tại K $\left(\text{K}\in \text{BN}\right)$. Chứng minh rằng: CK = 2MI.

d. Kẻ BD vuông góc với MC tại D $\left(\text{D}\in \text{MC}\right)$. Chứng minh rằng DK // BC.

Lời giải

a. Tính MN biết BC = 7 cm.

Xét $\Delta \text{ABC}$ có:  $\left\{\begin{array}{c}\text{AM = MB (gt)}\\ \text{AN = NC (gt)}\end{array}\right.$

 MN là đường trung bình của tam giác

 $\Rightarrow \text{MN = }\frac{1}{2}\text{BC = }\frac{1}{2}.7=3,5\left(\text{cm}\right)$

b. Chứng minh rằng tứ giác MNCB là hình thang cân.

Vì MN là đường trung bình của tam giác

$\Rightarrow \text{MN // BC }\Rightarrow \text{BMNC}$ là hình thang

Mà $\widehat{\text{MBC}}\text{ = }\widehat{\text{NCB}}$ ($\Delta \text{ABC}$ cân tại A) →BMNC là hình thang cân

c. Kẻ MI vuông góc với BN tại I, $\left(\text{I}\in \text{BN}\right)$ và CK vuông góc với BN tại K $\left(\text{K}\in \text{BN}\right)$. Chứng minh rằng: CK = 2MI.

Kẻ AH vuông góc với BN

Xét $\Delta \text{ABH}$ có: $\left\{\begin{array}{c}\text{AM = MB (gt)}\\ \text{MI // AH (}\perp \text{BN)}\end{array}\right.$

 MI là đường trung bình của tam giác

 $\Rightarrow \text{MI = }\frac{1}{2}\text{AH }$

Xét $\Delta \text{AHN}$ và  $\Delta \text{CKN}$ có: $\left\{\begin{array}{c}\text{AN = NC}\left(gt\right)\\ \widehat{\text{ANH}}\text{ = }\widehat{\text{CNK}}\left(\text{dd}\right)\\ \widehat{\text{AHN}}\text{ = }\widehat{\text{CKN}}=90°\end{array}\right.$

 $\Rightarrow \Delta \text{AHN = }\Delta \text{CKN}$ (cạnh huyền – góc nhọn)

$\Rightarrow \text{AH = CK}$ (cặp cạnh tương ứng)

$\Rightarrow \text{MI = }\frac{1}{2}\text{CK}$ (đpcm)

d. Kẻ BD vuông góc với MC tại D $\left(\text{D}\in \text{MC}\right)$. Chứng minh rằng DK // BC.

Gọi O là giao điểm của BN và CM. Suy ra O là trọng của  

Kéo dài AO cắt BC tại P $\left(\text{P}\in \text{BC}\right)$.

Vì tam giác ABC cân tại A nên đường trung tuyến AP đồng thời là đường trung trực của BC  $\Rightarrow \text{BC}\perp \text{AP}$

Vì $\text{O}\in \text{AP}\Rightarrow \text{OB = OC }\Rightarrow \Delta \text{OBD = }\Delta \text{OCK}$ (cạnh huyền – góc nhọn)

$\Rightarrow \text{OD = OK}$ (cặp cạnh tương ứng)

Suy ra $\Delta \text{ODK}$ cân tại O.

Vì tam giác OBC cân tại O nên đường trung tuyến OP đồng thời là đường phân giác của $\widehat{\text{BOC}}$ suy ra OA là phân giác của  $\widehat{\text{DOK}}$

Mà $\Delta \text{DOK}$ cân tại O nên OA cũng là đường cao.

$\Rightarrow \text{OA}\perp \text{DK}\Rightarrow \text{AP}\perp \text{DK}$ mà  $\text{BC}\perp \text{AP}$

Suy ra DK // BC (đpcm)

Bài 5. (0,5 điểm) Tìm giá trị lớn nhất của biểu thức:   ${\text{A = 7 – x}}^{\text{2}}\text{– 3x}$

Lời giải

Ta có: ${\text{A = 7 – x}}^{\text{2}}\text{– 3x = –}\left({\text{x}}^{\text{2}}\text{+ 2x}\frac{\text{3}}{\text{2}}\text{ + }\frac{\text{9}}{\text{4}}\right)=-{\left(\text{x + }\frac{\text{3}}{\text{2}}\right)}^2+\frac{37}{4}\le \frac{37}{4},\forall \text{x}$

Dầu bằng xảy ra  $\iff \text{x + }\frac{3}{2}=0\iff \text{x = –}\frac{\text{3}}{\text{2}}$

Vậy giá trị lớn nhất của  $\text{A = }\frac{37}{4}\iff \text{x = – }\frac{3}{2}$

…………………………………………………………………………………………

[Năm 2022] Đề thi Giữa kì 1 Toán lớp 8 có đáp án (11 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 3

I. PHẦN TRẮC NGHIỆM (2 ĐIỂM) 

Hãy viết vào tờ giấy thi chữ cái in hoa đứng trước câu trả lời đúng

Câu 1. Khai tiển biểu thức x³-8x³ ta được kết quả là:

A. (x-2y)³

B. x³-2y³            

C. (x-2y)(x²+2xy+4y²)

D. x³-6x²y + 12xy²-8y³

Câu 2. Kết quả phép tính -x²(3-2x)là:

A. 3x²-2x³

B.2x³-3x²

C.-3x³+2x²

D.-4x²

Câu 3. Để  4y²-12y +trở thành một hằng đảng thức. Giá trị trong ô vuông là:

A. 6                       B. 9 

C. – 9                     D. Một kết quả khác

Câu 4. Biểu thức 101² – 1 có giá trị bằng

A. 100                   B. 100²

C. 102000              D. Một kết quả khác

Câu 5. Giá trị của biểu thức x²+2xy+y² tại x = – 1 và y = – 3 bằng

A. 16                     B. – 4

C. 8                        D. Một kết quả khác

Câu 6. Biết 4x(x²-25)=0, các số x tìm được là:

A. 0; 4; 5               B. 0; 4

C. -5; 0; 5              D. Một kết quả khác

Câu 7. 

A. -2x +4 =2(2-x)                                    B. -2x+4 = -2(2-x)

C.  -2x +4= -2(x+2)                                  D. -2x+4= 2(x-2)

Câu 8. Thực hiện phép nhân x(x-y)

A.x²-y                    B.x-xy

C.x-x²                D.x²-xy

II. PHẦN TỰ LUẬN (8 ĐIỂM)

Bài 1 (1,5đ): Phân tích các đa thức sau thành nhân tử

a. 36a⁴-y²                                                   b. 6x² +x -2

Bài 2 (1,5đ). Tìm x, biết:

a. x( x-4)+1 = 3x-5                                      b. 2x³-3x²-2x+3= 0

Bài 3 (1,5đ). 

a. Cho biểu thức A= x³-9x²+27x -27 . Tính giá trị của A khi x = 1.

b. Tìm đa thức thương và đa thức dư trong phép chia đa thức A (x) cho B (x). Biết:

A(x)= 2x³+x²-x+ a và B(x) = x-2

Bài 4 (3,0đ). Cho hình bình hành ABCD có AB > BC. Đường phân giác của góc cắt AB tại M, đường phân giác của góc cắt CD tại N.

a. Chứng minh AM = CN.

b. Chứng minh tứ giác DMBN là hình bình hành.

c. Gọi H, K lần lượt là hình chiếu của N và N trên BN và DM. Chứng minh hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường.

Bài 5 (0,5đ). Tìm giá trị lớn nhất của biểu thức:

A = -2x² -10y² +4xy +4x+ 4y +2016

HƯỚNG DẪN CHẤM

I. PHẦN TRẮC NGHIỆM (2 ĐIỂM)

Câu 1: C      (0,25đ)

Câu 2: B      (0,25đ)

Câu 3: B      (0,25đ)

Câu 4: C      (0,25đ)

Câu 5: A     (0,25đ)

Câu 6: C      (0,25đ)

Câu 7: A     (0,25đ)

Câu 8: D     (0,25đ)

II. PHẦN TỰ LUẬN (8 ĐIỂM)

Bài 1 

a. 36a⁴-y2= (6a)²-y²= (6a-y)(6a+y)      (0,75đ)                                      

b.6x² +x -2 = 6x²+4x -3x -2

  = 2x( 3x+2) – (3x+2) = (2x-1)(3x+2)  (0,75đ)   

Bài 2 

a. x(x-4) +1 = 3x-5

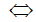     x(x-1) – 6(x-1)=0  (0,25đ)

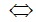     (x-1)(x-6)=0       (0,25đ)

 

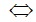
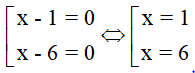
Vậy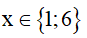là giá trị cần tìm.           (0,25đ)                            

b. 2x³-3x²-2x+3= 0

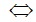  x²( 2x-3) -(2x-3) =0           (0,25đ)

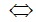  (2x-3)(x²-1) =0

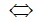     (2x-3)(x-1)(x+1)=0  (0,25đ)

    …..

 

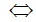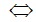
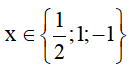
Vậy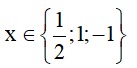 là giá trị cần tìm.    (0,25đ)

Bài 3 

a. Xét biểu thức:

A= x³-9x²+27x -27

   = x³ -3.x².3 +3.x.3²– 3³

   =(x-3)³   (0,25đ)

Với x = 1 biểu thức A được viết lại như sau:

A=(1-3)³ = -8

Vậy A = – 8 khi x = 1                          (0,25đ)

b.Thực hiện đúng được phép chia  A(x)= 2x³+x²-x+ a cho B(x) = x-2, tìm được thương bằng:2x²+5x +9 và dư bằng a + 18.           (1,0đ)

Bài 4 

Vẽ đúng hình         (0,25đ)

a. Chứng minh được AM = CN           (1,25đ)

b. Chứng minh được tứ giác DMBN là hình bình hành                (1đ)

c. Lập luận chặt chẽ chỉ ra được hai đoạn thẳng AC và MN cắt nhau tại trung điểm của mỗi đường         (0,5đ)

Bài 5 

A = -2x² -10y² +4xy +4x+ 4y +2016

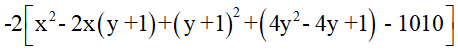   =  (0,25đ)

   = -2( x-y-1)² -2(2y-1)² +2020

GTLN của A bằng 2020 khi 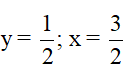            (0,25đ)

[Năm 2022] Đề thi Giữa kì 1 Toán lớp 8 có đáp án (11 đề) – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Giữa Học kì 1

Năm học 2022 – 2023

Bài thi môn: Toán lớp 8

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

Đề 4

A. TRẮC NGHIỆM (3 điểm). 

Hãy chọn phương án trả lời đúng trong mỗi trường hợp sau:

1) Tích của đơn thức x² và đa thức 5x³ -x-1 là:

A.  5x⁶-x³-x² 

B. -5x⁵+ x³ +x²   

C. 5x⁵-x³-x²

D. 5x⁵-x-1

2) Đa thức 3x²-12được phân tích thành nhân tử là:

A. 3x(x-2)²

B. 3x( x²+4)

C. 3(x – 2)(x + 2)

D. x(3x – 2)(3x + 2)

3) Cho tứ giác ABCD biết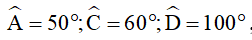 khi đó số đo góc B là

A. 150⁰                                                          B. 105⁰

C. 75⁰                                                            D. 30⁰

4) Đa thức x⁴-3x³+6x²-7x+m chia hết cho đa thức x – 1 khi m bằng

A. 0                                                               B. – 3

C. 3                                                                D. 1   

5) Giá trị nhỏ nhất của đa thức A= x²+4x+11 là

A. 7                                                               B. – 2

C. – 4                                                             D. 11

6) Cho tam giác ABC vuông tại A, O là trung điểm của BC. D là điểm đối xứng với A qua O. Đẳng thức nào sai trong các đẳng thức sau?

A.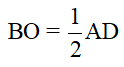                              B.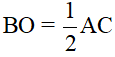

C. AB = CD                              D. AD = BC

B. TỰ LUẬN (7 điểm)

Câu 1 (2 điểm)

1) Tìm x biết x(x – 1) + x – 1 = 0

2) Tính giá trị biểu thức: A= (x-y)(x²+xy+y²⁾  +2y²tại 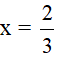và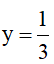

Câu 2 (2 điểm) Cho đa thức A= 2x⁴ + 3x³ – 4x² -3x +2 và đa thức B = x + 2

1) Làm tính chia đa thức A cho đa thức B.

2) Hãy phân tích đa thức thương của phép chia đa thức A cho đa thức B thành nhân tử.

Câu 3 (2,5 điểm) Cho hình bình hành ABCD trong đó có BC = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.

1) Chứng minh rằng tứ giác MNDC là hình bình hành.

2) Kẻ DE vuông góc với AB tại E, DE cắt MN tại F. Chứng minh F là trung điểm của DE.

3) Chứng minh rằng: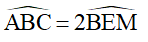

Câu 4 (0,5 điểm) Cho các số x, y, z thỏa mãn đồng thời:

x+ y+ z= 1; x²+y²+z²= 1; x³ + y³+z³ =1

Tính giá trị của biểu thức: M= x⁸+y¹¹+ z²⁰¹⁸

 

ĐÁP ÁN – THANG ĐIỂM

A. TRẮC NGHIỆM (3 ĐIỂM)

Câu 1: C     (0,5đ)

Câu 2: C      (0,5đ)

Câu 3: A     (0,5đ)

Câu 4: C      (0,5đ)

Câu 5: A     (0,5đ)

Câu 6: B      (0,5đ)

B. TỰ LUẬN (7 điểm)

Câu 1 

1) x(x – 1) + x – 1 = 0

  =>    (x – 1)(x + 1) = 0              (0,25đ)

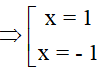                               (0,5đ)

Vậy 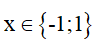                          (0,25đ)

2) A= (x-y)(x²+xy+y²⁾  +2y²  

       = x³ + y³                                                                    (0,5đ)

Tại 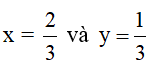 biểu thức A có giá trị là  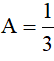       (0,5đ)

Câu 2. Thực hiện được đúng phép chia A= 2x⁴ + 3x³ – 4x² -3x +2 và đa thức B = x + 2

1)   (2x⁴ + 3x³ – 4x² -3x +2) : (x+2) = 2x³-x²-2x + 1     (1đ)

2)  2x³-x²-2x + 1= 2x( x²-1)-(x²-1) = (x² – 1)(2x-1)    (0,5đ)

         =(x-1)(x+1)(2x-1)                                           (0,5đ)

Câu 3 

1) Chỉ ra được MC // ND           (0,25đ)

Do đó tứ giác MNDC là hình bình hành        (0,5đ)

2) Chỉ ra được NF // AE                                          (0,25đ)

và N là trung điểm cạnh AD của tan giác DAE        (0,25đ)

→ F là trung điểm của DE                                       (0,5đ)

3) Ta có: 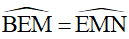 (cặp góc so le trong)

Chỉ ra được tam giác MED cân tại M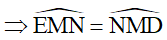 

Chỉ ra được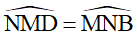       (0,25đ)

Do đó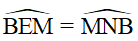 

Mặt khác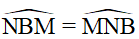 (tam giác BMN cân tại M)

Và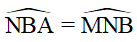 (cặp góc so le trong)

Vậy 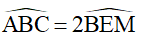     (0,25đ)

Câu 4. 

Ta có: (x+y+z)³ = x³+y³+z³ + 3(x+y)(y+z)(z+x)

Kết hợp với các điều kiện đã cho, ta có:(x+y)(y+z)(z+x)= 0

→ Một trong các thừa số của tích(x+y)(y+z)(z+x) phải bằng 0

Giả sử (x + y) = 0, kết hợp với điều kiện: x + y + z = 1 → z = 1

Kết hợp với điều kiện:  x²+y²+z²= 1→ x = y = 0

Vậy trong 3 số x, y, z phải có 2 số bằng 0 và 1 số bằng 1.           (0,25đ)

Vậy S = 1              (0,25đ)

Chú ý: Dưới đây là hướng dẫn cơ bản, bài làm của học sinh phải trình bày chi tiết. HS giải bằng nhiều cách khác nhau đúng vẫn cho điểm từng phần tương ứng.