Giải SBT Toán lớp 10 Bài tập cuối chương 4
Giải SBT Toán 10 trang 66 Tập 1
A. Trắc nghiệm
Bài 4.39 trang 66 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm A, B, C, D và O. Số các vectơ khác vectơ – không và cùng phương với là:
A. 6;
B. 3;
C. 4;
D. 2.
Lời giải:
Đáp án đúng là: A
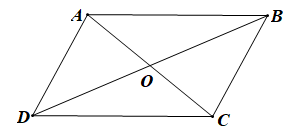
Các vectơ khác vectơ – không và cùng phương với là:
Vậy có 6 vectơ khác vectơ – không và cùng phương với
Vậy ta chọn phương án A.
Bài 4.40 trang 66 SBT Toán 10 Tập 1: Cho đoạn thẳng AC và B là một điểm nằm giữa A, C. Trong các khẳng định sau, khẳng định nào là một khẳng định đúng?
A. Hai vectơ và cùng hướng;
B. Hai vectơ và cùng hướng;
C. Hai vectơ và cùng hướng;
D. Hai vectơ và cùng hướng.
Lời giải:
Đáp án đúng là: C

Vì B nằm giữa A và C nên ta có:
• và ngược hướng. Do đó phương án A sai.
• và ngược hướng. Do đó phương án B sai.
• và cùng hướng. Do đó phương án C đúng.
• và ngược hướng. Do đó phương án D sai.
Vậy ta chọn phương án C.
Giải SBT Toán 10 trang 67 Tập 1
Bài 4.41 trang 67 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Gọi K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA. Trong các vectơ có đầu mút lấy từ các điểm A, B, C, D, K, L, M, O, có bao nhiêu vectơ bằng vectơ
A. 2;
B. 6;
C. 4;
D. 8.
Lời giải:
Đáp án đúng là: C
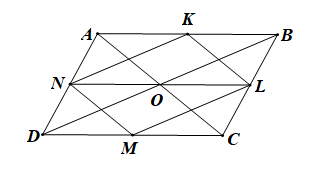
Vì ABCD là hình bình hành nên AB // CD và AB = CD.
Lại có K, L, M, N tương ứng là trung điểm các cạnh AB, BC, CD, DA
Nên AK = KB = DM = MC và NL // AB // CD
Do đó ABLN là hình bình hành (do AB // NL và AN // BL)
Suy ra AB = NL = CD
Mà O là tâm hình bình hành nên O là trung điểm của AC và BD
Do đó đường trung bình NL đi qua O
Và NO = OL =
Suy ra AK = KB = NO = OL = DM = MC.
Khi đó các vectơ bằng vectơ là:
Vậy có 4 vectơ bằng vectơ
Ta chọn phương án C.
Bài 4.42 trang 67 SBT Toán 10 Tập 1: Cho hình thoi ABCD có độ dài các cạnh bằng 1 và Khẳng định nào sau đây là đúng?
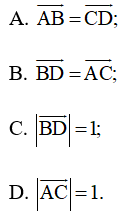
Lời giải:
Đáp án đúng là: D
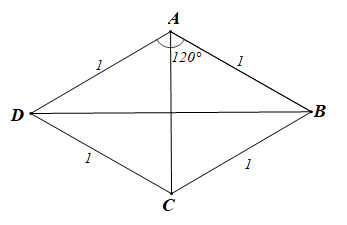
• Xét phương án A:
Vì ABCD là hình thoi nên AB // CD suy ra
Do đó phương án A là sai.
• Xét phương án B:
Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau.
Khi đó nên
Do đó phương án B là sai.
• Xét phương án C:
Vì ABCD là hình thoi có cạnh bằng 1 nên AD = AB = 1.
Xét DABD có AB = AD = 1 và áp dụng định lí cosin ta có:
BD2 = AD2 + AB2 – 2.AD.AB.cos
Þ BD2 = 12 + 12 – 2.1.1.cos120°
Þ BD2 = 3
Þ BD =
Khi đó
Do đó phương án C là sai.
• Xét phương án D:
Vì ABCD là hình thoi có cạnh bằng 1 nên AD = CD = 1 .
Mặt khác nên
Tam giác ADC có AD = DC nên là tam giác cân lại có
Suy ra DADC là tam giác đều
Þ AC = AD = CD = 1.
Khi đó
Do đó phương án D là đúng.
Bài 4.43 trang 67 SBT Toán 10 Tập 1: Cho tam giác ABC đều, trọng tâm G, có độ dài các cạnh bằng 3. Độ dài của vectơ bằng
Lời giải:
Đáp án đúng là: A
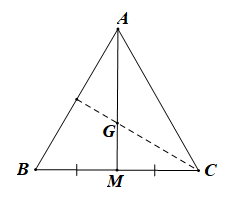
Tam giác ABC đều có cạnh bằng 3 nên AB = AC = 3 và
Gọi M là trung điểm của BC.
Khi đó ta có:
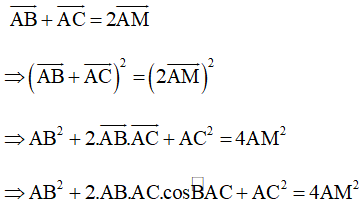
Þ 32 + 2.3.3.cos60° + 32 = 4.AM2
Þ 4.AM2 = 27
Þ AM2 =
Þ AM =
Vì G là trọng tâm tam giác ABC nên AG = AM
Þ AG =
Khi đó
Vậy ta chọn phương án A.
Bài 4.44 trang 67 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A và AB = 3, AC = 4. Độ dài của vectơ bằng
A.
B.
C. 4;
D. 2.
Lời giải:
Đáp án đúng là: B
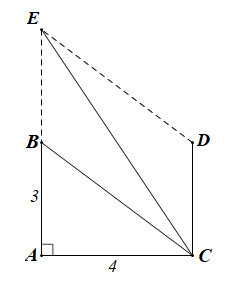
Gọi D là điểm thỏa mãn
Khi đó CD // AB và CD = AB (1)
Ta có:
Gọi E là điểm thỏa mãn BCDE là hình bình hành.
Khi đó CD // BE và CD = BE (2)
Từ (1) và (2) ta có: AB ≡ BE và AB = BE
Do đó B là trung điểm của AE
Þ AE = 2AB = 2.3 = 6.
Xét tam giác ACE vuông tại A, theo định lí Pythagore ta có:
CE2 = AC2 + AE2 = 42 + 62 = 52
Þ CE =
Vì ABCD là hình bình hành nên (quy tắc hình bình hành)
Vậy ta chọn phương án B.
Bài 4.45 trang 67 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 2, BC = 4 và Độ dài của vectơ bằng
A. 2;
B. 4;
C.
D.
Lời giải:
Đáp án đúng là: C
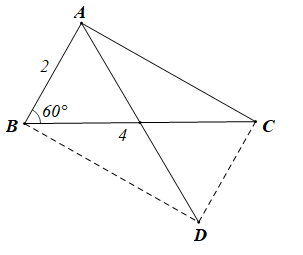
Xét DABC có AB = 2, BC = 4 và
Khi đó tam giác ABC là tam giác vuông tại A.
Ta có:
Gọi D là điểm thỏa mãn ABDC là hình bình hành
Khi đó
Hình bình hành ABDC có nên là hình chữ nhật.
Do đó AD = BC (hai đường chéo bằng nhau)
Vậy ta chọn phương án C.
Bài 4.46 trang 67 SBT Toán 10 Tập 1: Cho tam giác ABC và điểm I sao cho Khẳng định nào sau đây là một khẳng định đúng?
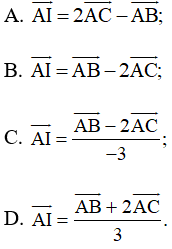
Lời giải:
Đáp án đúng là: D
Ta có:
Khi đó và là hai vectơ cùng phương, ngược hướng và IB = 2IC.
Khi đó điểm I nằm giữa hai điểm B và C sao cho IB = 2IC.
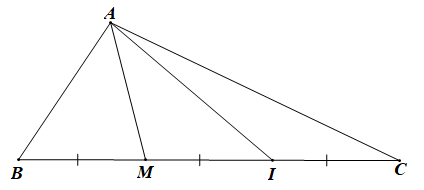
Gọi M là trung điểm của BI.
Khi đó M là trung điểm của BI, I là trung điểm của MC.
Vì I là trung điểm của MC nên ta có:
(1)
Vì M là trung điểm của BI nên ta có:
(2)
Thay (2) vào (1) ta được:
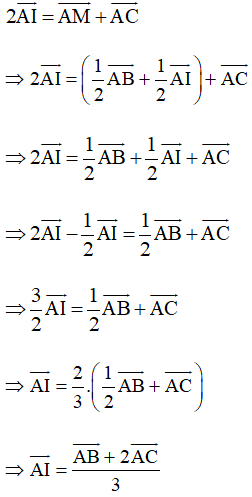
Vậy ta chọn phương án D.
Giải SBT Toán 10 trang 68 Tập 1
Bài 4.47 trang 68 SBT Toán 10 Tập 1: Gọi G là trọng tâm của tam giác ABC và M là trung điểm cạnh BC. Khẳng định nào sau đây là một khẳng định đúng?
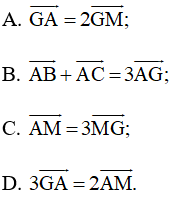
Lời giải:
Đáp án đúng là: B
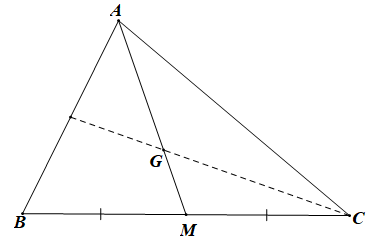
• Xét phương án A:
Vì G là trọng tâm của tam giác ABC nên AG = 2GM và G nằm giữa A, M.
Khi đó là hai vectơ ngược hướng
Nên
Do đó phương án A là sai.
• Xét phương án B:
Vì M là trung điểm của BC nên
Mà G là trọng tâm của tam giác ABC nên AG = AM
Hai vectơ và cùng hướng nên
Khi đó
Do đó phương án B là đúng.
• Xét phương án C:
Vì G là trọng tâm của tam giác ABC nên AM = 3MG và G nằm giữa A, M.
Khi đó là hai vectơ ngược hướng
Nên
Do đó phương án C là sai.
• Xét phương án D:
Ta có (chứng minh khi xét phương án B)
Do đó phương án D là sai.
Vậy ta chọn phương án B.
Bài 4.48 trang 68 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 1), B(2; −1), C(4; 6). Trọng tâm G của tam giác ABC có toạ độ là
A. (1; 2);
B. (2; 1);
C. (1; –2);
D. (–2; 1).
Lời giải:
Đáp án đúng là: A
G là trọng tâm của tam giác ABC nên ta có:
Þ G(1; 2)
Vậy ta chọn phương án A.
Bài 4.49 trang 68 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–3; 3), B(5; −2) và G(2; 2). Toạ độ của điểm C sao cho G là trọng tâm tam giác ABC là
A. (5; 4);
B. (4; 5);
C. (4; 3);
D. (3; 5).
Lời giải:
Đáp án đúng là: B
Vì G là trọng tâm của tam giác ABC nên ta có:
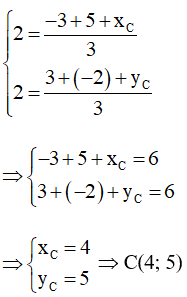
Vậy ta chọn phương án B.
Bài 4.50 trang 68 SBT Toán 10 Tập 1: Cho hình vuông ABCD với độ dài cạnh bằng a. Tích vô hướng bằng:
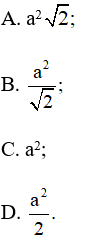
Lời giải:
Đáp án đúng là: C
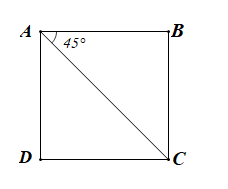
Vì ABCD là hình vuông nên DABC vuông cân tại B
Do đó:
•
• AC = (theo định lí Pythagore)
Ta có: = AB.AC.cos
= a.a..cos45°
= a.a.
= a2.
Do đó = a2.
Vậy ta chọn phương án C.
Bài 4.51 trang 68 SBT Toán 10 Tập 1: Cho hai vectơ cùng khác Khi đó tương đương với
A. và cùng phương;
B. và ngược hướng;
C. và cùng hướng;
D.
Lời giải:
Đáp án đúng là: C
Ta có:
Do đó để
và cùng hướng.
Vậy ta chọn phương án C.
Bài 4.52 trang 68 SBT Toán 10 Tập 1: Cho hai vectơ cùng khác Khi đó tương đương với
A. và cùng phương;
B. và ngược hướng;
C. và cùng hướng;
D.
Lời giải:
Đáp án đúng là: B
Ta có:
Do đó để
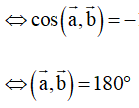
và ngược hướng.
Vậy ta chọn phương án B.
Bài 4.53 trang 68 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 1, BC = 2 và Tích vô hướng bằng
A.
B.
C. 3;
D. –3.
Lời giải:
Đáp án đúng là: D
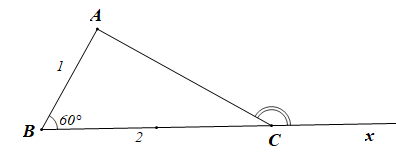
Ta có: = BC.CA.cos
Kéo dài tia BC ta được tia Cx
Khi đó:
Tam giác ABC có AB = 1, BC = 2
Nên AB = BC
Lại có
Do đó DABC vuông tại A.
Suy ra:
• AC =
•
Mà (do hai góc và kề bù)
Do đó = BC.CA.cos
= 2..cos150°
= 2.
= –3.
Vậy ta chọn phương án D.
Giải SBT Toán 10 trang 69 Tập 1
Bài 4.54 trang 69 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(–1; 5) và C(3m; 2m –1). Tất cả các giá trị của tham số m sao cho AB ⊥ OC là
A. m = –2;
B. m = 2;
C. m = ±2;
D. m = 3.
Lời giải:
Đáp án đúng là: B
Với A(2; −1), B(–1; 5) và C(3m; 2m –1) ta có:
và
Để AB ⊥ OC thì
Û −3.3m + 6.(2m – 1) = 0
Û −9m + 12m – 6 = 0
Û 3m = 6
Û m = 2.
Vậy ta chọn phương án B.
Bài 4.55 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A với AB = 1, AC = 2. Lấy M, N, P tương ứng thuộc các cạnh BC, CA, AB sao cho 2BM = MC, CN = 2NA, AP = 2PB. Giá trị của tích vô hướng bằng
A.
B.
C. 0;
D. 1.
Lời giải:
Đáp án đúng là: C
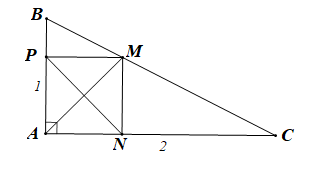
Ta có:
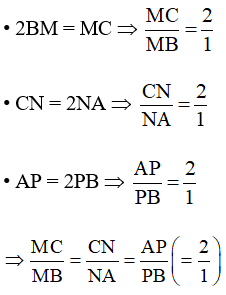
Þ MN // AB và PM // AC (định lí Talet đảo)
Þ ANMP là hình bình hành
Mặt khác:
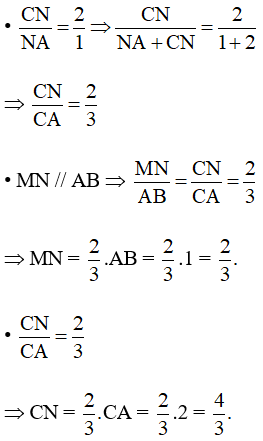
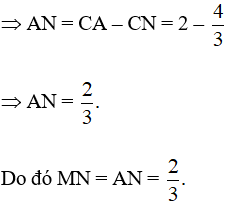
Hình bình hành ANMP có MN = AN nên là hình thoi
Khi đó hai đường chéo AM và PN vuông góc với nhau
Vậy ta chọn phương án C.
Bài 4.56 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC đều các cạnh có độ dài bằng 1. Lấy M, N, P lần lượt thuộc các cạnh BC, CA, AB sao cho BM = 2MC, CN = 2NA và AM ⊥ NP. Tỉ số của bằng
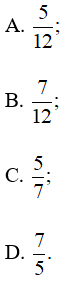
Lời giải:
Đáp án đúng là: A
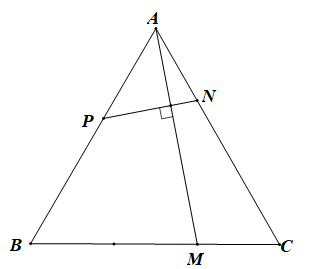
Giả sử (x > 0)
Ta có:
• Ta có: MB = 2MC nên M nằm giữa B và C
Hay
Do đó
Tương tự ta cũng có và
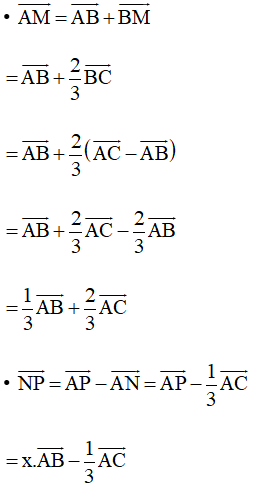
Mặt khác ta có: AM ⊥ NP
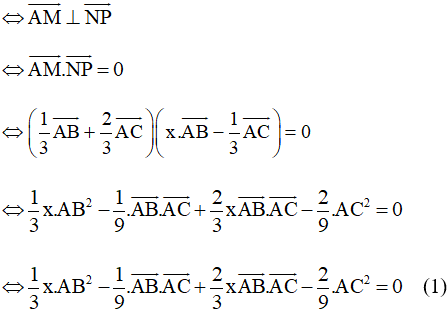
Tam giác ABC đều có độ dài cạnh bằng 1 nên AB = AC = BC = 1 và
Ta có:
= 1.1.cos60° =
Khi đó:
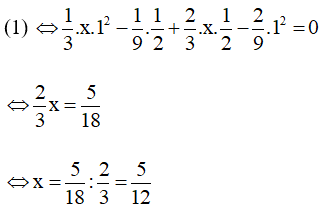
(thỏa mãn)
Vậy
Ta chọn phương án A.
Bài 4.57 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC đều có độ dài các cạnh bằng 3a. Lấy điểm M thuộc cạnh BC sao cho MB = 2MC. Tích vô hướng của hai vectơ và bằng
A.
B.
C. a2;
D. –a2.
Lời giải:
Đáp án đúng là: B
Ta có: MB = 2MC nên M nằm giữa B và C
Hay
Do đó
Tương tự ta có
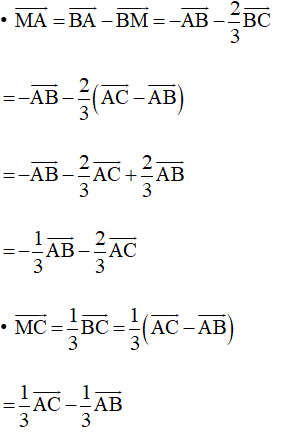
• Khi đó:
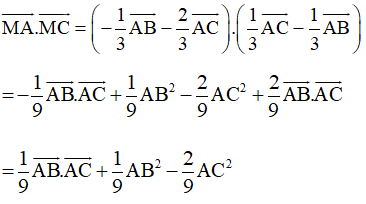
• Tam giác ABC đều có độ dài cạnh bằng 3a nên AB = AC = BC = 3a và
Ta có:
= 3a.3a.cos60° =
Do đó
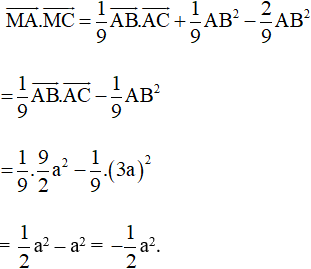
Vậy a2.
Ta chọn phương án B.
Bài 4.58 trang 69 SBT Toán 10 Tập 1: Cho tam giác ABC. Tập hợp các điểm M thoả mãn là
A. đường tròn tâm A bán kính BC.
B. đường thẳng đi qua A và song song với BC.
C. đường tròn đường kính BC.
D. đường thẳng đi qua A và vuông góc với BC.
Lời giải:
Đáp án đúng là: A
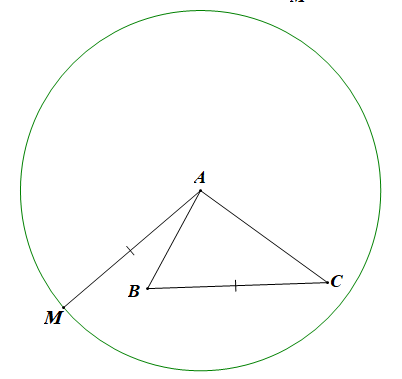
Ta có:
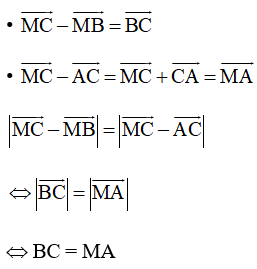
Û BC = MA
Do đó tập hợp điểm M thỏa mãn yêu cầu đề bài là đường tròn tâm A bán kính BC (như hình vẽ trên).
Vậy ta chọn phương án A.
Giải SBT Toán 10 trang 70 Tập 1
B. Tự luận
Bài 4.59 trang 70 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Gọi M, theo thứ tự là trung điểm của BC, AD. Gọi I, J lần lượt là giao điểm của BD với AM, CN. Xét các vectơ khác có đầu mút lấy từ các điểm A, B, C, D, M, N, I, J, O.
a) Hãy chỉ ra những vectơ bằng vectơ những vectơ cùng hướng với
b) Chứng minh rằng BI = IJ = JD.
Lời giải:
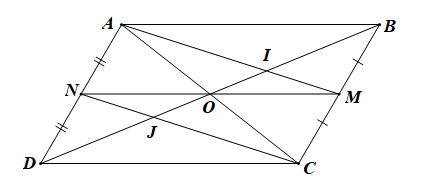
a) ABCD là hình bình hành có M, N lần lượt là trung điểm của BC, AD
Nên MN là đường trung bình của hình bình hành
Þ MN // AB // DC và MN = AB = DC.
Þ
Vậy những vectơ bằng vectơ là:
Lại có O là tâm hình bình hành nên O là trung điểm của AC và BD
Do đó NO là đường trung bình của DADC
Þ NO // DC
Chứng minh tương tự ta cũng có OM // DC
Do đó ba điểm M, O, N thẳng hàng.
Vậy những vectơ cùng hướng với là:
b) Xét tam giác ABC có: AM, BO là hai đường trung tuyến của tam giác
Mà AM cắt BO tại I
Do đó I là trọng tâm của DABC.
và (tính chất trọng tâm) (1)
Tương tự ta cũng có J là trọng tâm của DADC.
và (tính chất trọng tâm) (2)
Mặt khác BO = DO (do O là trung điểm của BD) (3)
Từ (1), (2) và (3) ta có: 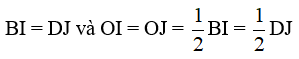
Mà 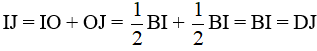
Vậy BI = IJ = JD.
Bài 4.60 trang 70 SBT Toán 10 Tập 1: Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.
a) Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm.
b) Gọi G là trọng tâm của tam giác ABC. Đặt và Hãy biểu thị các vectơ sau qua hai vectơ và
Lời giải:
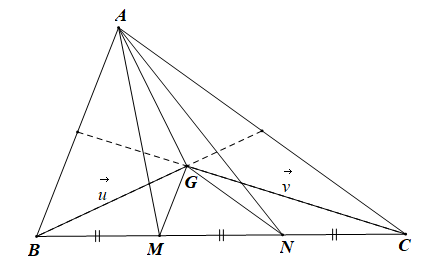
a) Giả sử G, G’ lần lượt là trọng tâm của DABC, DAMN.
Sử dụng kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có:
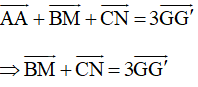
Mặt khác: M, N lần lượt lấy theo thứ tự trên cạnh BC sao cho BM = MN = NC nên ta có:
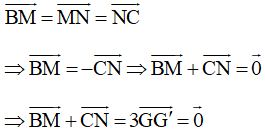
Suy ra điểm G và G’ trùng nhau.
Do đó hai tam giác ABC và AMN có cùng trọng tâm.
b) • Vì G là trọng tâm của tam giác ABC nên
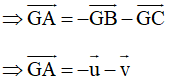
• Từ BM = MN = NC suy ra
Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm G ta có:
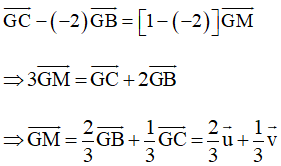
Tương tự ta cũng có:
Bài 4.61 trang 70 SBT Toán 10 Tập 1: Cho tam giác ABC có AB = 4, AC = 5 và
a) Tính tích vô hướng
b) Lấy các điểm M, N thoả mãn và (x ≠ –1). Xác định x sao cho AN vuông góc với BM.
Lời giải:
a) Ta có:
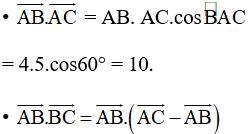
= 10 – 42
= 10 – 16
= –6
Vậy
b) Ta có
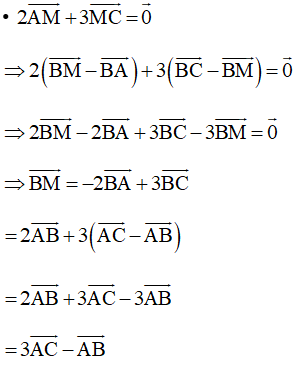
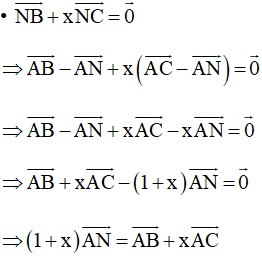
Do đó:
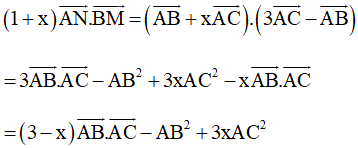
= (3 – x).10 – 42 + 3x.52
= 30 – 10x – 16 + 75x
= 65x + 14
Để AN ⊥ BM thì
(với x ≠ –1)
Û 65x + 14 = 0
Û x =
Vậy với x = thì AN ⊥ BM.
Bài 4.62 trang 70 SBT Toán 10 Tập 1: Cho hình bình hành ABCD. Gọi M, N theo thứ tự là trung điểm các cạnh AB, CD. Lấy P thuộc đoạn DM và Q thuộc đoạn BN sao cho DP = 2PM, BQ = xQN. Đặt và
a) Hãy biểu thị các vectơ qua hai vectơ và
b) Tìm x đề A, P, Q thằng hàng.
Lời giải:
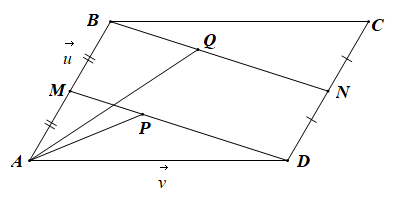
a) • Vì P thuộc đoạn DM sao cho DP = 2PM
Nên
Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:
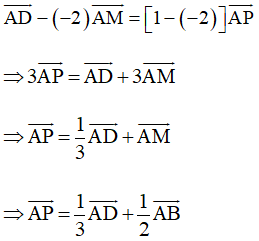
(vì M là trung điểm của AB)
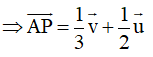
• Vì Q thuộc đoạn BN sao cho BQ = xQN
Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:
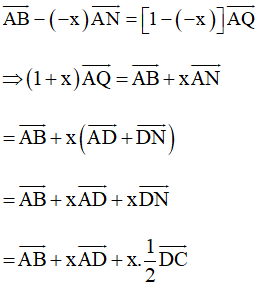
(vì N là trung điểm của CD)
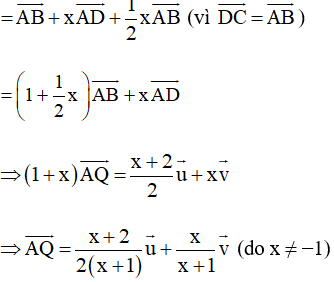
b) Với và
Để A, P, Q thẳng hàng thì hai vectơ và cùng phương
Þ x + 2 = 2x
Û x = 2 (thỏa mãn x ≠ –1)
Vậy x = 2 thì ba điểm A, P, Q thẳng hàng.
Bài 4.63 trang 70 SBT Toán 10 Tập 1: Cho tam giác ABC với trọng tâm G. Lấy điểm A’, B’ sao cho Gọi G’ là trọng tâm của tam giác A’B’C. Chứng minh rằng GG’ song song với AB.
Lời giải:
Theo kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có:
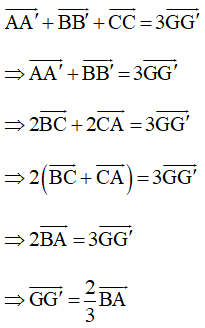
Do đó cùng phương với
Suy ra GG’ // AB (do G và G’ không nằm trên đường thẳng AB)
Bài 4.64 trang 70 SBT Toán 10 Tập 1: Cho tứ giác lồi ABCD không có hai cạnh nào song song. Gọi E, F theo thứ tự là trung điểm AB, CD. Gọi K, L, M, N lần lượt là trung điểm của AF, CE, BF, DE.
a) Chứng minh rằng tứ giác KLMN là một hình bình hành.
b) Gọi I là giao điểm của KM, LN. Chứng minh rằng E, I, F thẳng hàng.
Lời giải:
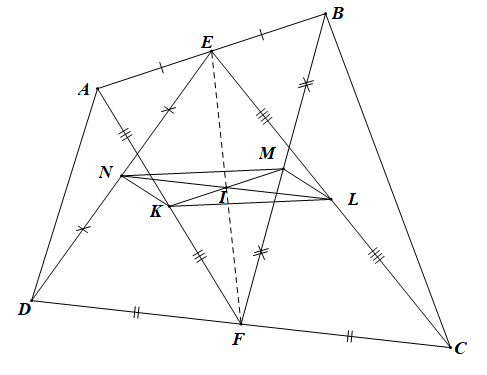
a) • Vì E là trung điểm của AB nên
F là trung điểm của CD nên
• Vì K là trung điểm của AF, L là trung điểm của CE, theo kết quả của Bài tập 4.12, trang 58, Toán 10, Tập một, ta có:
Tương tự:
M là trung điểm của BF, N là trung điểm của DE, nên ta có:
Do đó
Þ KL = NM và KL // NM
Þ KLMN là một hình bình hành.
b) Do KLMN là hình bình hành
Mà I là giao điểm của KM, LN nên I là trung điểm chung của KM, LN.
Khi đó ta có:
(do F là trung điểm của DC)
Do đó
Suy ra hai vectơ và cùng phương
Do đó E, I, F thẳng hàng.
Bài 4.65 trang 70 SBT Toán 10 Tập 1: Cho hình thang vuông ABCD có BC = 1, AB = 2 và AD = 3. Gọi M là trung điểm của AB.
a) Hãy biểu thị các vectơ theo hai vectơ và
b) Gọi N là trung điểm CD, G là trọng tâm tam giác MCD, và I là điểm thuộc cạnh CD sao cho 9IC = 5ID. Chứng minh rằng A, G, I thẳng hàng.
c) Tính độ dài các đoạn thẳng AI và BI.
Lời giải:
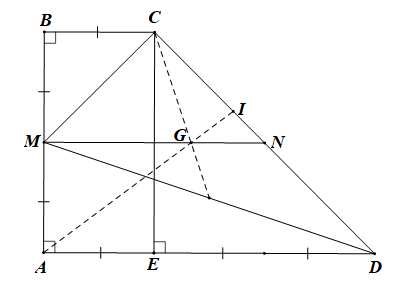
a) Vì M là trung điểm của AB nên
Gọi E là hình chiếu của C trên AD. Khi đó
Tứ giác ABCE có nên là hình chữ nhật
Þ EA = CB = 1
Mà AD = 3 do đó AE = AD
Mà (do ABCE là hình chữ nhật)
• Ta có:
Mà (do ABCE là hình chữ nhật)
Và
Vậy và
b) Vì G là trọng tâm của tam giác MCD nên ta có:
ABCD là hình chữ nhật nên cũng là hình bình hành
Do đó
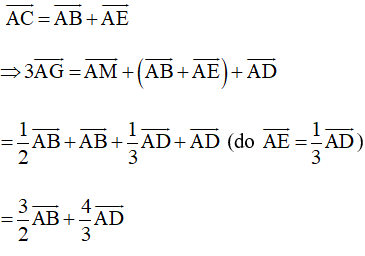
Vì I thuộc cạnh CD nên hai vectơ và ngược hướng nhau
Lại có 9IC = 5ID nên hay
Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm A ta có:
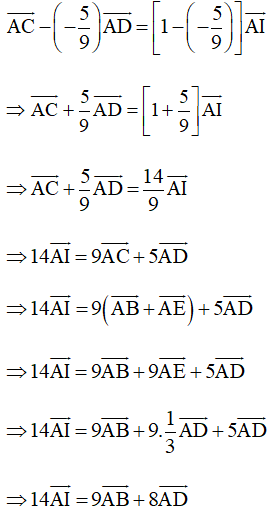
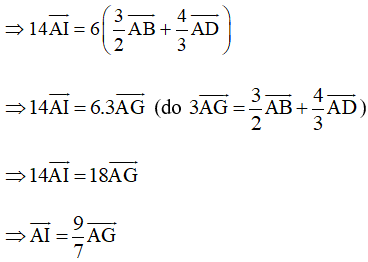
Do đó hai vectơ và cùng phương
Suy ra ba điểm A, I, G thẳng hàng.
c) • Theo câu a ta có
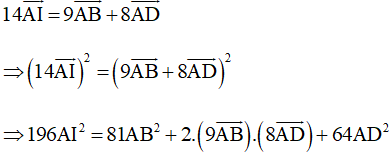
Mà AB ⊥ AD nên
Do đó ta có: 196AI2 = 81AB2 + 64AD2
Þ 196AI2 = 81.22 + 64.32 = 900
Þ AI2 =
Þ AI =
• Ta có:
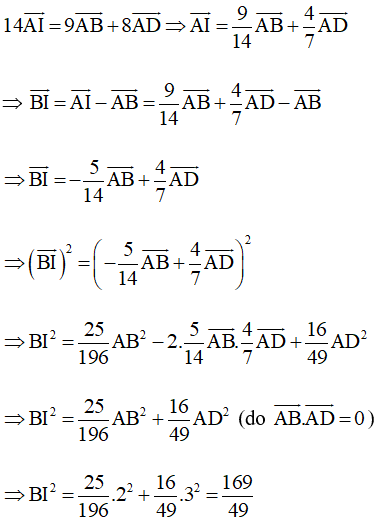
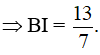
Vậy AI = và BI =
Bài 4.66 trang 71 SBT Toán 10 Tập 1: Cho bốn điểm A, B, C, D trong mặt phẳng. Chứng minh rằng
Lời giải:
Ta có:
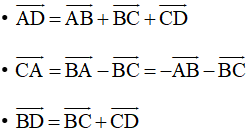
Suy ra:
= 0.
Vậy
Bài 4.67 trang 71 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba ![]()
a) Tính các tích vô hướng ![]()
b) Tìm góc giữa hai vectơ và
Lời giải:
a) Với = (1; 2), = (3; –4) và = (–5; 3) ta có:
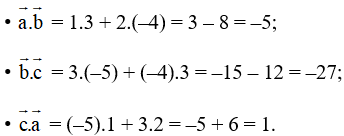
b) Với ![]() ta có:
ta có:
•
• = (–2; –1)
• = 1.(–2) + 2.(–1) = –2 – 2 = –4.
Mà cos
Vậy góc giữa hai vectơ và khoảng 143°7’48”.
Bài 4.68 trang 71 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(–2; 1), B(1; 4) và C(5; −2).
a) Chứng minh rằng A, B, C là ba đỉnh của một tam giác. Tìm toạ độ trọng tâm G của tam giác ABC.
b) Tìm toạ độ trực tâm H và tâm đường tròn ngoại tiếp I của tam giác ABC.
Lời giải:
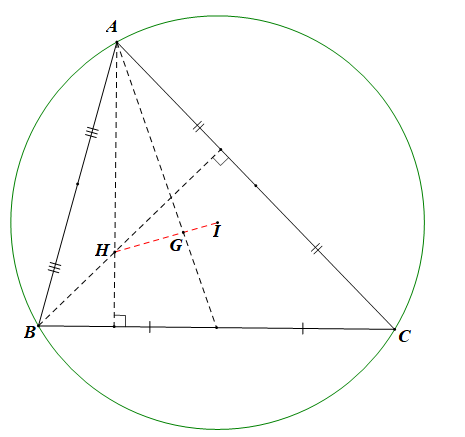
a) Với A(–2; 1), B(1; 4) và C(5; −2) ta có:
= (3; 3) và = (7; –3)
Vì nên hai vectơ và không cùng phương
Do đó ba điểm A, B, C không thẳng hàng
Vậy A, B, C là ba đỉnh của một tam giác.
Vì G là trọng tâm của tam giác ABC nên ta có:
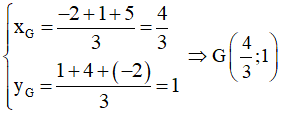
Vậy tọa độ trọng tâm của tam giác ABC là: .
b) *Tìm tọa độ trực tâm H của tam giác ABC:
Vì H là trực tâm của tam giác ABC nên AH ⊥ BC và BH ⊥ AC
Hay và
Giả sử H(x; y) là tọa độ trực tâm tam giác ABC
Với A(–2; 1), B(1; 4), C(5; −2) và H(x; y) ta có:
• = (x + 2; y – 1) và = (4; –6)
= 4.(x + 2) – 6.(y – 1) = 0
Þ 4x – 6y = –14
Þ 2x – 3y = –7 (1)
• = (x – 1; y – 4) và = (7; –3)
= 7.(x – 1) – 3.(y – 4) = 0
Þ 7x – 3y = –5 (2)
Trừ vế theo vế (2) cho (1) ta có: 5x = 2
Þ x =
Thay x = vào (1) ta được: 2. – 3y = –7
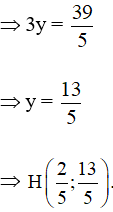
Vậy tọa độ trực tâm của tam giác ABC là
* Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác ABC:
Theo kết quả phần a) của Bài 4.15, trang 54, Sách Bài tập, Toán 10, tập một ta có:
với M là trung điểm của BC.
Giả sử I(a; b) là tọa độ tâm đường tròn ngoại tiếp tam giác ABC
Với A(–2; 1), B(1; 4), C(5; −2), và I(a; b) ta có:
•
• M là trung điểm của BC nên
Þ M(3; 1)
= (3 – a; 1 – b)
= (6 – 2a; 2 – 2b)
Ta có
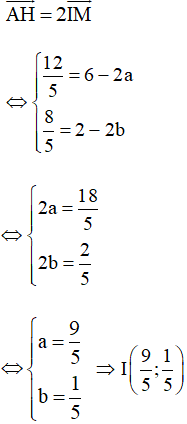
Vậy tọa độ tâm đường tròn ngoại tiếp tam giác ABC là
Bài 4.69 trang 71 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm A(2; −1), B(5; 3) và C(–2; 9).
a) Tìm điểm D thuộc trục hoành sao cho B, C, D thẳng hàng.
b) Tìm điểm E thuộc trục hoành sao cho EA + EB nhỏ nhất.
c) Tìm điểm F thuộc trục tung sao cho vectơ có độ dài ngắn nhất.
Lời giải:
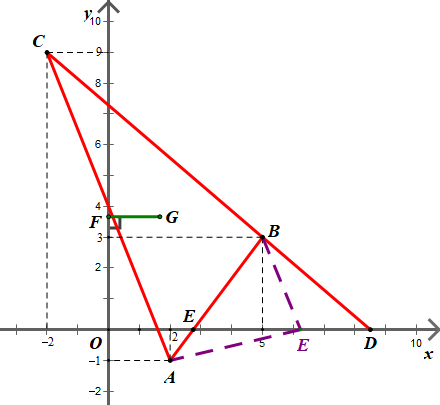
a) Giả sử D(a; 0) là điểm thuộc trục hoành.
Với B(5; 3), C(–2; 9) và D(a; 0) ta có:
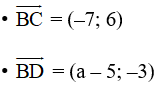
Vì ba điểm B, C, D thẳng hàng nên ta có: và là hai vectơ cùng phương
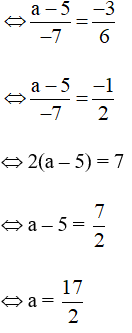
Vậy là điểm cần tìm.
b) Ta có: A(2; −1), B(5; 3) là hai điểm nằm về hai phía của trục hoành
Do đó với mỗi điểm E nằm trên trục hoành ta luôn có EA + EB ≥ AB
Suy ra EA + EB ngắn nhất là bằng AB
Điều này xảy ra khi và chỉ khi E là giao điểm của AB và trục hoành Ox
Û 3 điểm A, E, B thẳng hàng
và là hai vectơ cùng phương
Giả sử E(b; 0) là điểm thuộc trục hoành.
Với A(2; −1), B(5; 3) và E(b; 0) ta có:
• = (3; 4)
• = (b – 2; 1)
Khi đó và là hai vectơ cùng phương
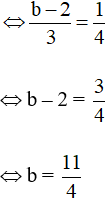
Vậy là điểm cần tìm.
c) Gọi G là trọng tâm của tam giác ABC.
Khi đó với A(2; −1), B(5; 3) và C(–2; 9) ta có:
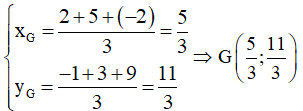
Với điểm F bất kì ta có:
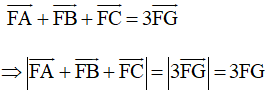
Để vectơ có độ dài ngắn nhất thì FG có độ dài ngắn nhất
Mà F là điểm nằm trên trục tung
Do đó F là hình chiếu vuông góc của G lên Oy.
Þ Hoành độ của F là x = 0 và tung độ của F bằng với tung độ của G là y =
Vậy
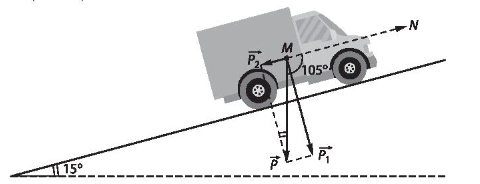
Bài 4.70 trang 71 SBT Toán 10 Tập 1: Một ô tô có khối lượng 2,5 tấn chạy từ chân lên đỉnh một con dốc thẳng. Tính công của trọng lực tác động lên xe, biết dốc dài 50 m và nghiêng 15° so với phương nằm ngang (trong tính toán, lấy gia tốc trọng trường bằng 10 m/s²).
Lời giải:
Đổi 2,5 tấn = 2 500 kg.
Trọng lực của ô tô có độ lớn bằng = mg = 2 500 . 10 = 25 000 (N)
Trọng lực ![]() của ô tô hợp với hướng chuyển dời một góc là:
của ô tô hợp với hướng chuyển dời một góc là:
α = 90° + 15° = 105°.
Trọng lực được phân tích thành hai thành phần và nên ta có:
( có phương vuông góc với mặt dốc, có phương song song với mặt dốc)
Ta thấy không có tác dụng với chuyển dời của xe và ngược hướng với .
Do đó công của trọng lực tác động lên xe bằng:
A =
= 25 000 . 50 . cos105°
≈ –323 524 (J)
Vậy công của trọng lực tác động lên xe bằng khoảng –323 524 J.
Xem thêm các bài giải SBT Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 11: Tích vô hướng của hai vectơ
Bài 12: Số gần đúng và sai số
Bài 13: Các số đặc trưng đo xu thế trung tâm
Bài 14: Các số đặc trưng đo độ phân tán