Lý thuyết Toán lớp 10 Bài 2: Tổng và hiệu của hai vectơ
A. Lý thuyết Tổng và hiệu của hai vectơ
1. Tổng của hai vectơ
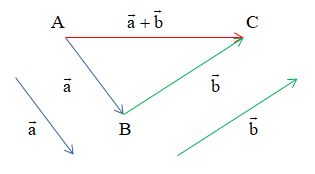
Cho hai vectơ và . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho . Khi đó được gọi là tổng của hai vectơ và và được kí hiệu là .
Vậy .
Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.
Quy tắc ba điểm
Với ba điểm M, N, P, ta có .
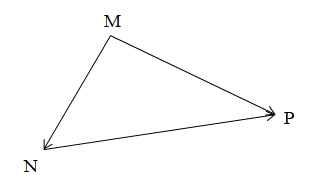 Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.
Ví dụ: Cho các điểm A, B, C, D, E, F phân biệt. Thực hiện phép cộng các vectơ:
.
Hướng dẫn giải
Áp dụng quy tắc ba điểm, ta có:
.
.
.
Quy tắc hình bình hành
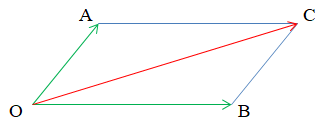
Nếu OACB là hình bình hành thì ta có .
Ví dụ: Cho hình chữ nhật MNPQ và hai vectơ như hình bên. Tính tổng của hai vectơ và .
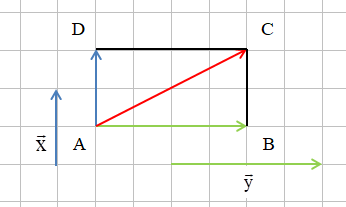
Hướng dẫn giải
Ta có .
Suy ra .
Theo quy tắc hình bình hành, ta có .
Vậy .
2. Tính chất của phép cộng các vectơ
Phép cộng vectơ có các tính chất sau:
+ Tính chất giao hoán: .
+ Tính chất kết hợp: .
+ Với mọi , ta luôn có: .
Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ ,kí hiệu là với .
Ví dụ: Cho tứ giác MNPQ. Thực hiện các phép cộng vectơ sau:
a) .
b) .
Hướng dẫn giải
Áp dụng tính chất giao hoán và tính chất kết hợp của phép cộng vectơ, ta được:
a) .
b) .
Chú ý: Cho vectơ tùy ý .
Ta có .
Tổng hai vectơ đối nhau luôn bằng vectơ-không: .
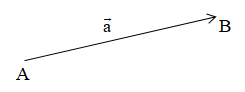
3. Hiệu của hai vectơ
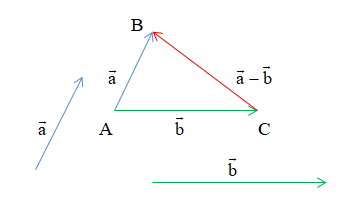
Cho hai vectơ và . Hiệu của hai vectơ và là vectơ \ và kí hiệu là .
Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.
Ví dụ: Cho các điểm D, E, F, G phân biệt. Thực hiện các phép trừ vectơ sau: .
Hướng dẫn giải
Ta có: .
.
Chú ý: Cho ba điểm O, A, B, ta có:.
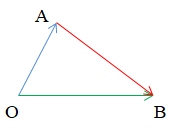 Ví dụ: Cho hình vuông ABCD và một điểm M tùy ý. Thực hiện các phép trừ vectơ sau: .
Ví dụ: Cho hình vuông ABCD và một điểm M tùy ý. Thực hiện các phép trừ vectơ sau: .
Hướng dẫn giải
Ta có .
.
4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác
Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi .
Điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Ví dụ: Cho hình bình hành ABCD có tâm O. Hai điểm E, F lần lượt là trung điểm AB, BC. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
a) .
b) .
Hướng dẫn giải
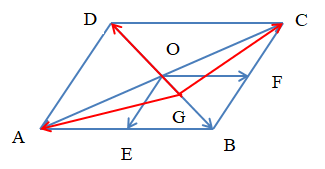 a) Vì ABCD là hình bình hành tâm O nên O là trung điểm AC (tính chất hình bình hành).
a) Vì ABCD là hình bình hành tâm O nên O là trung điểm AC (tính chất hình bình hành).
Lại có E là trung điểm AB (gt)
Do đó OE là đường trung bình của tam giác ABC.
Suy ra OE // BC và OE = = BF (với F là trung điểm BC).
Khi đó ta có tứ giác OEBF là hình bình hành.
Áp dụng quy tắc hình bình hành cho OEBF, ta được: .
Vì ABCD là hình bình hành tâm O nên O là trung điểm AC và BD (tính chất hình bình hành).
Do đó và .
Ta có
.
Vậy .
b) Vì G là trọng tâm của tam giác ABC nên .
Theo quy tắc ba điểm, ta có: .
Ta có
.
Vậy .
B. Bài tập tự luyện
Bài 1. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:
a) .
b) .
c) .
Hướng dẫn giải
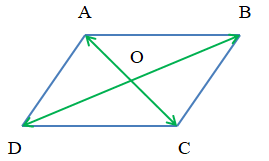
a) Vì O là tâm của hình bình hành ABCD nên O là trung điểm của AC và BD (tính chất hình bình hành).
Do đó ta có (1) và (2).
Lấy (1) + (2) vế theo vế ta được: .
b) Vì ABCD là hình bình hành nên BA // DC và BA = DC.
Mà ngược hướng.
Do đó .
Ta suy ra .
Ta có .
c) Ta có O là trung điểm BD nên DO = OB.
Mà cùng hướng.
Do đó .
Ta có .
Bài 2. Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài các vectơ:
a) .
b) .
Hướng dẫn giải
a) Vì ABCD là hình vuông nên .
Do đó .
Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Py ‒ ta ‒ go)
⇔ AC2 = a2 + a2 = 2a2
⇒ AC = .
Vậy .
b) Vì ABCD là hình vuông nên ta có BD = AC = và AD = CB.
Mà ngược hướng.
Do đó .
Ta có .
Do đó .
Vì O là tâm của hình vuông ABCD nên O là trung điểm BD.
Do đó OD = .
Vậy .
Bài 3. Một con thuyền trôi theo hướng nam vận tốc 25 km/h, dòng nước chảy theo hướng đông với vận tốc 10 km/h. Tính độ dài vectơ tổng của hai vectơ nói trên (làm tròn kết quả đến hàng trăm).
Hướng dẫn giải
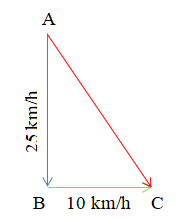
Gọi A là vị trí con thuyền xuất phát.
Vận tốc của con thuyền được biểu diễn bởi .
Vận tốc của dòng nước được biểu diễn bởi .
Khi đó ta có vectơ tổng của hai vectơ nói trên là .
Do đó độ lớn của vectơ cần tìm là:.
Vì con thuyền trôi theo hướng nam và dòng nước chảy theo hướng đông.
Nên ta có AB ⊥ BC.
Ta có độ lớn vận tốc con thuyền là 25 km/h.
Suy ra = AB = 25.
Ta có độ lớn vận tốc dòng nước là 10 km/h.
Suy ra = BC = 10.
Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Py ‒ ta ‒ go)
⇔ AC2 = 252 + 102 = 725.
⇒ AC = ≈ 26,93.
Vậy độ dài vectơ tổng của hai vectơ nói đến trong bài xấp xỉ bằng 26,93 (km/h).
Xem thêm các bài tóm tắt lý thuyết Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 1: Khái niệm vectơ
Lý thuyết Bài 2: Tổng và hiệu của hai vectơ
Lý thuyết Bài 3: Tích của một số với một vectơ
Lý thuyết Bài 4: Tích vô hướng của hai vectơ
Lý thuyết Bài 1: Số gần đúng và sai số