Giải bài tập Toán lớp 10 Bài tập cuối chương III
A. Trắc nghiệm
Giải Toán 10 trang 44 Tập 1 Kết nối tri thức
Bài 3.12 trang 44 Toán lớp 10: Cho tam giác ABC có . Khẳng định nào sau đây là đúng?
a,
A.
B.
C.
D.
Phương pháp giải:
Diện tích tam giác ABC:
Lời giải:
Diện tích tam giác ABC:
Mà .
Chọn D
b,
A.
B.
C.
D.
Phương pháp giải:
Định lí sin:
Lời giải:
Theo định lí sin, ta có:
A. đúng
B.
Mà
Vậy B sai.
C. (Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)
D. (Loại vì không có dữ kiện về góc A nên không thể tính R theo a.)
Chọn A
c,
A.
B.
C.
D.
Phương pháp giải:
Định lí sin:
Định lí cos:
Lời giải:
A. (Loại)
Vì: Theo định lí cos ta có:
Không đủ dữ kiện để suy ra
B. (Loại)
Theo định lí sin, ta có:
C. (sai vì theo câu a, )
D.
Theo định lý cos ta có:
(*)
Mà .
Thay vào (*) ta được:
=> D đúng.
Chọn D
Bài 3.13 trang 44 Toán lớp 10: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
LG a
A.
B.
C.
D.
Phương pháp giải:
+) Định lí cos:
+) Công thức tính diện tích:
Lời giải:
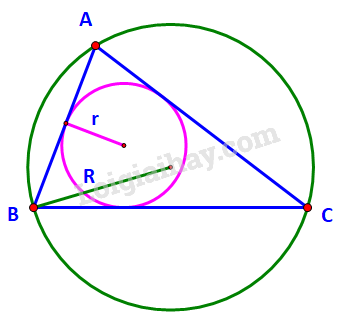
a, Chọn đáp án B
A.
Ta có: . Mà nên suy ra
Vậy A sai.
B.
Ta có:
Mà
Vậy B đúng
C.
Sai vì theo định lí cos ta có:
D.
Sai vì
b, Chọn đáp án A
A.
Ta có:
Vậy A đúng.
B.
Sai vì (Do )
C.
Không đủ dữ kiện để kết luận.
Nếu thì
Nếu thì
D.
Ta có
Mà
Vậy D sai.
LG b
A.
B.
C.
D.
Phương pháp giải:
Giá trị lượng giác của hai góc bù nhau:
;
Lời giải:
A.
Ta có:
=> A đúng.
B.
Sai vì
C. Không đủ dữ kiện để kết luận.
Nếu thì
Nếu thì
D.
Ta có . Mà
=> D sai.
Chọn A
B. Tự luận
Bài 3.14 trang 44 Toán lớp 10: Tính giá trị của các biểu thức sau:
a)
b)
c)
d)
Phương pháp giải:
Bảng giá trị lượng giác của các góc đặc biệt
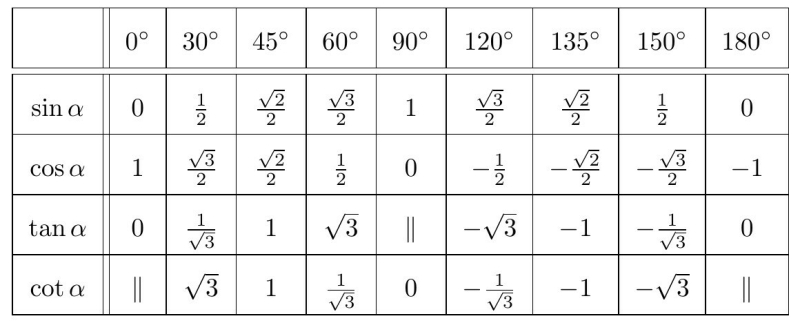
Lời giải:
a)
Ta có:
Thay vào M, ta được:
b)
Ta có:
Thay vào N, ta được:
c)
Ta có:
Thay vào P, ta được:
d)
Ta có:
Thay vào P, ta được:
Bài 3.15 trang 44 Toán lớp 10: Cho tam giác ABC có . Tính .
Phương pháp giải:
Định lí sin:
Lời giải:
Theo định lí sin:
+) Ta có:
Mà
+) Mặt khác:
Mà
+) Diện tích tam giác ABC là:
+) Lại có:
Bài 3.16 trang 44 Toán lớp 10: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a)
b) và
c) (công thức đường trung tuyến).
Phương pháp giải:
a) Giá trị lượng giác của hai góc bù nhau:
b) Định lí cos: cho tam giác tương ứng.
c) Suy ra từ b, lưu ý rằng:
Lời giải:
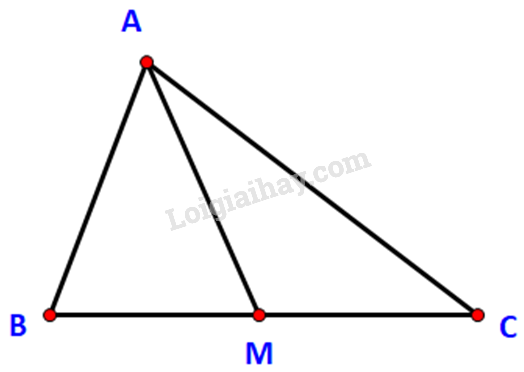
a) Ta có:
Hay
b) Áp dụng định lí cos trong tam giác AMB ta có:
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:
c) Từ (1), suy ra
Từ (2), suy ra
Cộng vế với vế ta được:
Mà: (do AM là trung tuyến)
(đpcm)
Cách 2:
Theo ý a, ta có:
Từ đẳng thức (1): suy ra
Thế vào biểu thức (2), ta được:
Lại có: (do AM là trung tuyến)
Bài 3.17 trang 44 Toán lớp 10: Cho tam giác ABC. Chứng minh rằng:
a) Nếu góc A nhọn thì
b) Nếu góc A tù thì
c) Nếu góc A vuông thì
Phương pháp giải:
a) Nếu góc A nhọn thì
b) Nếu góc A tù thì
c) Nếu góc A vuông thì
Định lí cos:
Lời giải:
Theo định lí cos ta có:
(1)
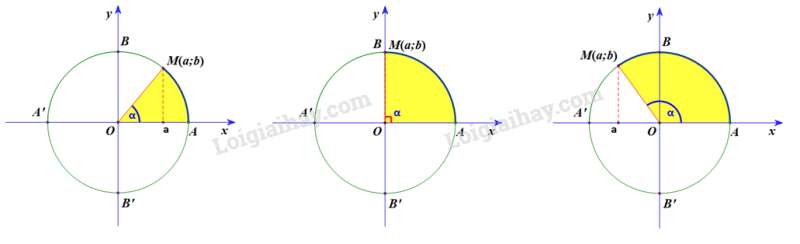
a) Nếu góc A nhọn thì
Từ (1), suy ra
b) Nếu góc A tù thì
Từ (1), suy ra
c) Nếu góc A vuông thì
Từ (1), suy ra
Giải Toán 10 trang 45 Tập 1 Kết nối tri thức
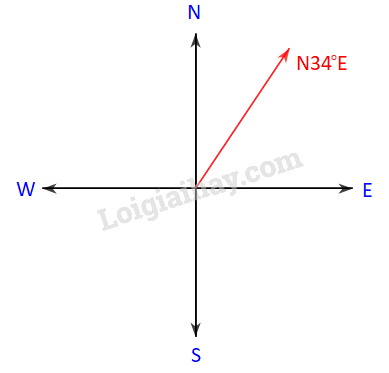
Bài 3.18 trang 45 Toán lớp 10: Trên biển, tàu B ở vị trí cách tàu A 53km về hướng . Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để đuổi kịp tàu B.
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?
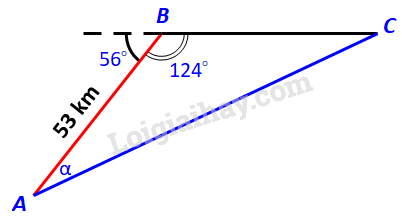
Phương pháp giải:
a) Tìm hướng chuyển động của A, tức là tính góc
Bước 1: Tính quãng đường BC, AC
Bước 2: Định lí sin:
=> , từ đó suy ra hướng của tàu A.
b) Bước 1: Tính góc C
Bước 2: Áp dụng định lí sin để suy ra t (thời gian đi cho đến khi gặp nhau)
Lời giải:
a)
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có:
Trong đó:
hoặc (loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc .
b) Xét tam giác ABC, ta có:
Theo định lí sin, ta có
Mà
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.
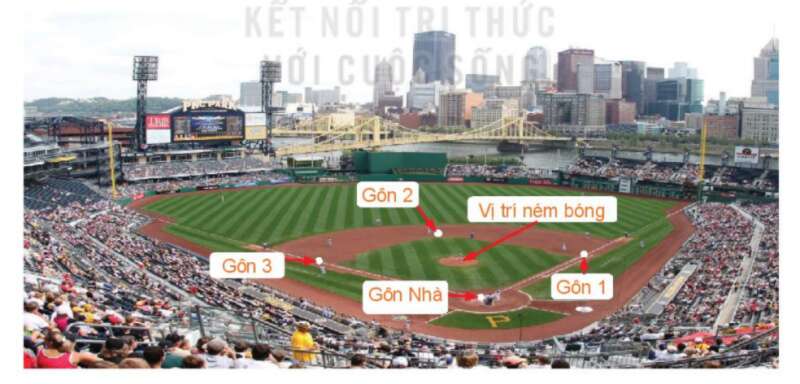
Bài 3.19 trang 45 Toán lớp 10: Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4 m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.
Phương pháp giải:
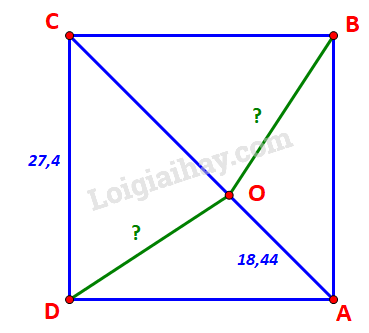
Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.
Vậy ta cần tính các đoạn thẳng OB và OD
Bước 1: Tính đường chéo AC, từ đó suy ra độ dài OC.
Bước 2: Vận dụng định lí cos trong tam giác OCD để suy ra OD.
Lời giải:
Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.
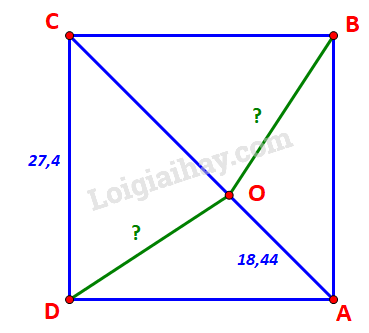
Ta có:
Xét tam giác OCD ta có:
Định lí cos:
Trong đó
Dễ thấy (c.g.c)
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 6: Hệ thức lượng trong tam giác
Bài 7: Các khái niệm mở đầu
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vecto với một số