Giải bài tập Toán lớp 10 Bài 23: Quy tắc đếm
A. Các câu hỏi trong bài
Mở đầu trang 60 Toán 10 Tập 2: Đếm là một bài toán cổ xưa nhất của nhân loại. Trong khoa học và trong cuộc sống, người ta cần đếm các đối tượng để giải quyết các vấn đề khác nhau. Chẳng hạn như bài toán sau:
Mỗi mật khẩu của một trang web là một dãy có từ 2 tới 3 kí tự, trong đó kí tự đầu tiên là một trong 26 chữ cái in thường trong bảng chữ cái tiếng Anh (từ a đến z), mỗi kí tự còn lại là một chữ số từ 0 đến 9. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
Bài học này sẽ giúp em hiểu và áp dụng hai quy tắc đếm cơ bản để giải quyết bài toán trên.
Lời giải:
Sau khi học bài này, ta sẽ giải quyết được bài toán trên như sau:
Mỗi mật khẩu của một trang web là một dãy có từ 2 tới 3 kí tự nên ta có hai trường hợp.
• Trường hợp 1: độ dài mật khẩu là 2 kí tự. Chọn từng kí tự và áp dụng quy tắc nhân.
– Kí tự đầu tiên có 26 cách chọn trong các chữ cái in thường tiếng Anh.
– Kí tự thứ hai có 10 cách chọn trong các chữ số từ 0 đến 9.
Vậy, theo quy tắc nhân, ta có 26 . 10 = 260 cách chọn mật khẩu trong trường hợp 1.
• Trường hợp 2: độ dài mật khẩu là 3 kí tự. Chọn từng kí tự và áp dụng quy tắc nhân.
– Kí tự đầu tiên có 26 cách chọn trong các chữ cái in thường tiếng Anh.
– Kí tự thứ hai có 10 cách chọn trong các chữ số từ 0 đến 9.
– Kí tự thứ ba có 10 cách chọn trong các chữ số từ 0 đến 9.
Vậy, theo quy tắc nhân, ta có 26 . 10 . 10 = 2 600 cách chọn mật khẩu trong trường hợp 2.
Vì có hai trường hợp rời nhau, mật khẩu có thể rơi vào một trong hai trường hợp, nên ta áp dụng quy tắc cộng. Tổng số mật khẩu có thể là 260 + 2 600 = 2 860.
Hoạt động 1 trang 61 Toán 10 Tập 2: Chọn chuyến đi (H.8.1)
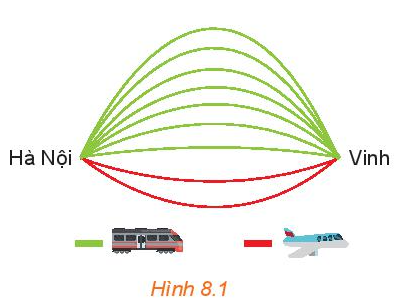
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay. Hỏi bạn An có bao nhiêu cách chọn chuyến đi?
Lời giải:
Bạn An có thể chọn đi tàu hỏa hoặc đi máy bay.
Có 7 cách đi bằng tàu hỏa và có 2 cách đi bằng máy bay nên có tất cả 9 cách đi bằng tàu hỏa hoặc máy bay.
Vậy bạn An có 9 cách chọn chuyến đi.
Hoạt động 2 trang 61 Toán 10 Tập 2: Chọn vé tàu (H.8.2)
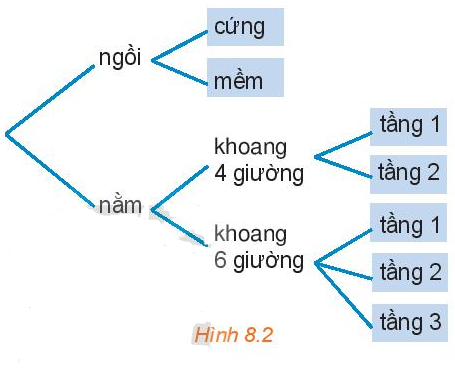
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có hai loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại khoang 4 giường và khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2 và tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Lời giải:
a) Toa ngồi có hai loại vé là ngồi cứng và ngồi mềm nên số loại vé ghế ngồi là 2.
Toa nằm có loại khoang 4 giường và khoang 6 giường.
– Khoang 4 giường có 2 loại vé: tầng 1 và tầng 2.
– Khoang 6 giường có 3 loại vé: tầng 1, tầng 2 và tầng 3.
Do đó, số loại vé giường nằm là 5.
Vậy có 2 loại vé ghế ngồi và 5 loại vé giường nằm.
b) Bạn An có thể chọn vé ghế ngồi hoặc vé giường nằm.
Nếu An chọn loại vé ghế ngồi: có 2 cách chọn.
Nếu An chọn loại vé giường nằm: có 5 cách chọn.
Vậy có 2 + 5 = 7 loại vé để bạn An lựa chọn.
Luyện tập 1 trang 62 Toán 10 Tập 2: Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Lời giải:
Hai số tự nhiên được gọi là nguyên tố cùng nhau nếu chúng có ước chung lớn nhất là 1. Do đó, hai số không nguyên tố cùng nhau khi ước chung của chúng khác 1.
Để tìm các số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35, ta tìm các số tự nhiên từ 1 đến 30 mà có ước chung lớn nhất với 35 khác 1.
Phân tích 35 ra thừa số nguyên tố ta có: 35 = 5 . 7.
Do đó, các số thỏa mãn yêu cầu đề bài là các số có một ước là 5 hoặc 7.
Các số có một ước là 5 mà lớn hơn 1 và nhỏ hơn hoặc bằng 30 là: 5, 10, 15, 20, 25, 30.
Các số có một ước là 7 mà lớn hơn 1 và nhỏ hơn hoặc bằng 30 là: 7, 14, 21, 28.
Vậy số các số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35 là: 6 + 4 = 10 (số).
Hoạt động 3 trang 62 Toán 10 Tập 2: Thầy Trung muốn đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam. Biết rằng từ Hà Nội vào Huế có thể đi bằng 3 cách: ô tô, tàu hỏa hoặc máy bay. Còn từ Huế vào Quảng Nam có thể đi bằng 2 cách: ô tô hoặc tàu hỏa (H.8.5).
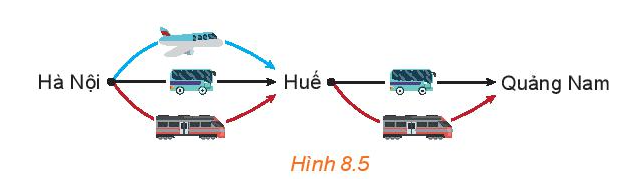
Hỏi thầy Trung có bao nhiêu cách chọn các phương tiện để đi từ Hà Nội vào Quảng Nam?
Lời giải:
Để đi từ Hà Nội vào Quảng Nam (mà đi qua Huế), đầu tiên ta đi từ Hà Nội vào Huế, rồi đi tiếp từ Huế vào Quảng Nam.
– Đi từ Hà Nội vào Huế có 3 cách chọn phương tiện.
– Với mỗi cách đi từ Hà Nội vào Huế thì có 2 cách chọn phương tiện để đi tiếp từ Huế vào Quảng Nam. Do đó, tổng số cách để đi từ Hà Nội vào Quảng Nam là:
2 + 2 + 2 = 3 . 2 = 6 (cách).
Vậy thầy Trung có 6 cách chọn các phương tiện để đi từ Hà Nội vào Quảng Nam.
Hoạt động 4 trang 63 Toán 10 Tập 2: Để lắp ghế vào một phòng chiếu phim, các ghế được gắn nhãn bằng một chữ cái in hoa (trong bảng 26 chữ cái tiếng Anh từ A đến Z) đứng trước và một số nguyên từ 1 đến 20, chẳng hạn X15, Z2,…
Hỏi có thể gắn nhãn tối đa được bao nhiêu ghế?
Lời giải:
Để gắn nhãn mỗi ghế, ta phải thực hiện gắn chữ cái in hoa, sau đó gẵn số.
– Gắn một chữ cái in hoa, có 26 cách (chọn 1 chữ trong 26 chữ cái).
– Sau đó gẵn số vào các ghế, chọn một số từ 1 đến 20 để gắn, có 20 cách.
Vậy có thể gắn nhãn tối đa cho 26 . 20 = 520 (ghế).
Luyện tập 2 trang 64 Toán 10 Tập 2: Tại kì World Cup năm 2018, vòng bảng gồm có 32 đội tham gia, được chia vào 8 bảng, mỗi bảng 4 đội thi đấu vòng tròn (mỗi đội chơi một trận với từng đội khác trong cùng bảng). Hỏi tổng cộng vòng bảng có bao nhiêu trận đấu?
Lời giải:
Xét một bảng bất kì. Trong một trận đấu có 4 cách chọn đội thứ nhất, 3 cách chọn đội thứ 2 để thi đấu nên có 4 . 3 = 12 (trận).
Vì hai đội chỉ gặp nhau đúng một lần nên thực tế trong mỗi bảng chỉ có 12 : 2 = 6 (trận).
Có tất cả 8 bảng nên số trận đấu của vòng bảng là: 6 . 8 = 48 (trận).
Vậy tổng cộng vòng bảng có 48 trận đấu.
Luyện tập 3 trang 64 Toán 10 Tập 2: Từ các chữ số 0, 1, 2, 3 có thể lập được bao nhiêu số thỏa mãn:
a) Là số tự nhiên có ba chữ số khác nhau.
b) Là số tự nhiên chẵn có ba chữ số khác nhau?
Lời giải:
a) Để lập số tự nhiên có ba chữ số khác nhau trên, ta cần thực hiện liên tiếp 3 công đoạn: chọn chữ số hàng trăm, chọn chữ số hàng chục và chọn chữ số hàng đơn vị.
+ Số cách chọn chữ số hàng trăm là: 3 cách (chọn 1 trong các số 1, 2, 3, vì chữ số hàng trăm không thể bắt đầu bằng 0).
+ Số cách chọn chữ số hàng chục là: 3 cách (chọn 1 trong các số 0, 1, 2, 3, trừ đi chữ số đã chọn ở hàng trăm).
+ Số cách chọn chữ số hàng đơn vị là: 2 cách.
Vậy theo quy tắc nhân, số các số thỏa mãn bài toán là: 3 . 3 . 2 = 18 (số).
b) Để số cần lập là số chẵn thì chữ số hàng đơn vị phải là 0 hoặc 2.
• Trường hợp 1: Chữ số hàng đơn vị là 0.
+ Số cách chọn chữ số hàng trăm là: 3 cách.
+ Số cách chọn chữ số hàng chục là: 2 cách.
Do đó, số các số lập được ở trường hợp này là: 3 . 2 = 6 (số).
+ Trường hợp 2: Chữ số hàng đơn vị là 2.
+ Số cách chọn chữ số hàng trăm là: 2 cách.
+ Số cách chọn chữ số hàng chục là: 2 cách.
Do đó, số các số lập được ở trường hợp này là: 2 . 2 = 4 (số).
Vì các trường hợp rời nhau nên theo quy tắc cộng, số các số chẵn có ba chữ số khác nhau lập được là: 6 + 4 = 10 (số).
Vận dụng trang 65 Toán 10 Tập 2: Khối lớp 10 của một trường trung học phổ thông có ba lớp 10A, 10B, 10C. Lớp 10A có 30 bạn, lớp 10B có 35 bạn, lớp 10C có 32 bạn. Nhà trường muốn chọn 4 bạn để thành lập đội cờ đỏ của khối sao cho có đủ đại diện của các lớp. Hỏi có bao nhiêu cách lựa chọn?
Lời giải:
Để chọn được 4 bạn lập thành đội cờ đỏ sao cho có đủ đại diện của các lớp, ta thấy có 3 trường hợp như sau:
• Trường hợp 1: chọn 2 bạn lớp 10A, 1 bạn 10B, 1 bạn 10C.
– Chọn 2 bạn của lớp 10A, vì vai trò hai bạn như nhau nên số cách chọn là: 30 . 29 : 2 = 435 cách chọn.
– Chọn 1 bạn của lớp 10B có 35 cách chọn.
– Chọn 1 bạn của lớp 10C có 32 cách chọn.
Do đó, số cách chọn là: 435 . 35 . 32 = 487 200 (cách chọn).
• Trường hợp 2: chọn 1 bạn lớp 10A, 2 bạn 10B, 1 bạn 10C.
– Chọn 1 bạn của lớp 10A có 30 cách chọn.
– Chọn 2 bạn của lớp 10B, vì vai trò hai bạn như nhau nên số cách chọn là: 35 . 34 : 2 = 595 cách chọn.
– Chọn 1 bạn của lớp 10C có 32 cách chọn.
Do đó, số cách chọn là: 30 . 595 . 32 = 571 200 (cách chọn).
• Trường hợp 3: chọn 1 bạn lớp 10A, 1 bạn 10B, 2 bạn 10C.
– Chọn 1 bạn của lớp 10A có 30 cách chọn.
– Chọn 1 bạn của lớp 10B có 35 cách chọn.
– Chọn 2 bạn của lớp 10C, vì vai trò hai bạn như nhau nên số cách chọn là: 32 . 31 : 2 = 496 cách chọn.
Do đó, số cách chọn là: 30 . 35 . 496 = 520 800 (cách chọn).
Vì các trường hợp là rời nhau nên ta áp dụng quy tắc cộng, vậy số cách chọn 4 bạn để thành lập đội cờ đỏ là: 487 200 + 571 200 + 520 800 = 1 579 200 (cách chọn).
B. Bài tập
Bài 8.1 trang 65 Toán 10 Tập 2: Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây minh hoạ và cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Lời giải:
Theo bài ra, ta vẽ được sơ đồ hình cây như sau:
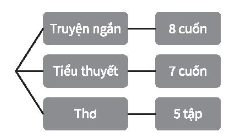
Số cách chọn một cuốn để đọc là: 8 + 7 + 5 = 20 (cách).
Vậy bạn Phong có 20 cách chọn một cuốn để đọc vào ngày cuối tuần.
Bài 8.2 trang 65 Toán 10 Tập 2: Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả là sấp hay ngửa. Hỏi nếu người đó gieo 3 lần thì có thể có bao nhiêu khả năng xảy ra?
Lời giải:
Người đó gieo một đồng xu 3 lần liên tiếp.
– Gieo lần 1 thì có thể xuất hiện mặt sấp hoặc ngửa nên số khả năng xảy ra là: 2.
– Gieo lần 2 tương tự lần 1, số khả năng xảy ra là: 2.
– Gieo lần 3 tương tự, số khả năng xảy ra là: 2.
Vì 3 lần gieo là liên tiếp nên theo quy tắc nhân, số khả năng xảy ra là: 2 . 2 . 2 = 8 (khả năng).
Bài 8.3 trang 65 Toán 10 Tập 2: Ở một loài thực vật, A là gene trội quy định tính trạng hoa kép, a là gene lặn quy định tính trạng hoa đơn.
a) Sự tổ hợp giữa hai gene trên tạo ra mấy kiểu gene? Viết các kiểu gene đó.
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gene đó?
Lời giải:
a) Sự tổ hợp giữa hai gene trội A và gene lặn a tạo 3 kiểu gene. Đó là: AA, Aa và aa.
b) Khi giao phối ngẫu nhiên thì cứ lấy 2 gene bất kì (có thể lấy giống nhau) để giao phối.
+ Với kiểu gene AA: có 3 kiểu giao phối (với AA, Aa, và aa);
+ Với kiểu gene Aa: có 2 kiểu giao phối (với Aa và aa);
+ Với kiểu gene aa: có 1 kiểu giao phối (với aa).
Vậy theo quy tắc cộng, có 3 + 2 + 1 = 6 kiểu giao phối khác nhau từ các kiểu gene trên khi giao phối ngẫu nhiên.
Bài 8.4 trang 65 Toán 10 Tập 2: Có bao nhiêu số tự nhiên
a) có 3 chữ số khác nhau?
b) là số lẻ có 3 chữ số khác nhau?
c) là số có 3 chữ số và chia hết cho 5?
d) là số có 3 chữ số khác nhau và chia hết cho 5?
Lời giải:
Để lập các số thỏa mãn yêu cầu bài toán, ta thực hiện liên tiếp 3 công đoạn: chọn chữ số hàng trăm, chọn chữ số hàng chục và chọn chữ số hàng đơn vị.
a) Lập số tự nhiên có 3 chữ số khác nhau.
– Chọn chữ số hàng trăm, có 9 cách chọn (vì chữ số hàng trăm phải khác 0, nên ta chọn 1 chữ số trong các chữ số 1, 2, …, 9);
– Chọn chữ số hàng chục có 9 cách chọn (do các chữ số khác nhau nên chọn 1 chữ số trong các chữ số 0, 1, 2, …, 9, trừ đi chữ số đã chọn ở hàng trăm);
– Chọn chữ số hàng đơn vị có 8 cách chọn (tương tự như chọn chữ số hàng chục).
Vậy theo quy tắc nhân, số các số tự nhiên có 3 chữ số khác nhau là: 9 . 9 . 8 = 648 (số).
b) Lập số tự nhiên là số lẻ có 3 chữ số khác nhau.
– Chọn chữ số hàng đơn vị là chữ số lẻ có 5 cách chọn (chọn 1 trong các chữ số 1, 3, 5, 7, 9);
– Chọn chữ số hàng trăm có 8 cách chọn (khác 0 và khác chữ số hàng đơn vị);
– Chọn chữ số hàng chục có 8 cách chọn (khác chữ số hàng đơn vị và hàng trăm).
Vậy theo quy tắc nhân, số các số tự nhiên là số lẻ có 3 chữ số khác nhau là: 5 . 8 . 8 = 320 (số).
c) Lập số tự nhiên có 3 chữ số và chia hết cho 5.
– Chọn chữ số hàng đơn vị có 2 cách chọn (chọn 0 hoặc chọn 5);
– Chọn chữ số hàng trăm có 9 cách chọn (khác 0);
– Chọn chữ số hàng chục có 10 cách chọn (do các chữ số không cần khác nhau).
Vậy theo quy tắc nhân, số các số tự nhiên có 3 chữ số và chia hết cho 5 là: 2 . 9 . 10 = 180 (số).
d) Lập số tự nhiên có 3 chữ số khác nhau và chia hết cho 5. Có 2 trường hợp.
+ Trường hợp 1: Chữ số hàng đơn vị là 0;
Chọn chữ số hàng trăm có 9 cách;
Chọn chữ số hàng chục có 8 cách.
Do đó có 9 . 8 = 72 cách.
+ Trường hợp 2: Chữ số hàng đơn vị là 5;
Chọn chữ số hàng trăm có 8 cách;
Chọn chữ số hàng chục có 8 cách.
Do đó có 8 . 8 = 64 cách.
Vì 2 trường hợp là rời nhau nên theo quy tắc cộng, số các số tự nhiên có 3 chữ số khác nhau và chia hết cho 5 là: 72 + 64 = 136 (số).
Bài 8.5 trang 65 Toán 10 Tập 2: a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu mật khẩu khác nhau?
Lời giải:
a) Để lập một mật khẩu chương trình máy tính, ta cần thực hiện ba công đoạn liên tiếp:
– Chọn kí tự thứ nhất: có 10 cách chọn (chọn 1 chữ số trong 10 chữ số từ 0 đến 9).
– Chọn kí tự thứ hai: tương tự kí tự thứ nhất, có 10 cách chọn.
– Chọn kí tự thứ ba: tương tự trên, có 10 cách chọn.
Vậy theo quy tắc nhân, có thể tạo được số mật khẩu là: 10 . 10 . 10 = 1 000 (mật khẩu).
b) Để lập một mật khẩu chương trình máy tính theo quy định mới, ta cần thực hiện ba công đoạn liên tiếp:
– Chọn kí tự thứ nhất từ tập 26 chữ từ A đến Z: có 26 cách chọn.
– Chọn kí tự thứ hai là chữ số: có 10 cách chọn.
– Chọn kí tự thứ ba là chữ số: có 10 cách chọn.
Do đó, theo quy tắc nhân, số cách tạo mật khẩu mới là: 26 . 10 . 10 = 2 600 (mật khẩu).
Vậy quy định mới có thể tạo được nhiều hơn quy định cũ số mật khẩu là:
2 600 – 1 000 = 1 600 (mật khẩu).
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 7
Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Bài 25: Nhị thức Newton
Bài tập cuối chương 8